三浦折紙超材料結構數字化設計與模型驗證1)

陳 耀 葉王杰 史佳遙 馮 健

(東南大學混凝土及預應力混凝土結構教育部重點實驗室,國家預應力工程技術研究中心,南京 211189)

引言

近年來,隨著計算機科學、計算幾何學和數論等領域的發展[1],折紙折痕分析及設計技術快速發展[2-5],以折痕設計為核心研究內容的折紙結構受到各領域研究人員的青睞.折紙結構已應用于土木建筑[2]、航空航天[6-7]、柔性電子[8]、生物醫學[9-11]、超材料[12-15]、機器人[16-18]、光學[19]等領域.

早期,折紙僅作為一項滿足人們審美需求的藝術形式,Yoshizawa 等創造了可供人們交流的折紙語言,并通過平面幾何、立體幾何、微分幾何、球面三角學理論等數學原理建立了折紙藝術與折紙科學之間的聯系[20].此后,折紙藝術不斷發展成為現代折紙科學.Miura(三浦)[21]率先發明了三浦折紙構型(又稱三浦折疊),并將其應用于可折展的太陽能帆板.另一方面,超材料由于具有可調節的材料特性,近年來發展迅猛,Yu 等[22]綜述了各種力學超材料胞元結構拓撲優化的重要進展,其中包括蜂窩結構、晶格結構和折紙超材料結構,分析了其彈性模量、泊松比、體積模量等與常規結構不同的材料特性.Fang 等[23]深入研究了四折痕折紙基本單元組合的自鎖特性,為開發擁有可編程性能的折紙超材料提供了有效途徑.Wang 等[24]研究了一種基于三浦折疊的折紙超材料,可通過幾何重構和形態變化主動調整材料的電磁和力學性能.

為了便于生成折紙結構的復雜三維模型、推廣應用于緩沖吸能結構及可展結構,諸多學者對三浦折紙構型開展了深入研究與衍生拓展.Gattas 等[25]考慮了折痕方向、折痕形式、結構的可展性與平面折疊性等因素,提出了廣義三浦折紙構型的設計方法.文獻[26-28]建立了折紙折痕構型的圖論表達方法,并結合優化算法研發了多種新型折紙構型.基于經典三浦折紙模式,Gattas 和You[29]提出了一種曲線折痕折紙構型的參數化設計方法.此外,為了將折紙構型應用于非零厚度的三維結構,Chen 等[30]引入三浦折紙的機構運動學模型,并推廣至厚板折紙結構.文獻[31-33]基于圖論方法,提出了一種利用無向和有向子圖生成二維折痕圖案的方法,為折紙結構開展幾何、力學性能分析等提供了便利.Li 等[34]綜述了近年來折紙超材料的幾何設計、力學分析、性能實現和制造技術之間協同等.Tachi[35]指出,將折紙應用于現實生活時,控制其三維構型極為重要,以便產生的折疊狀態與所需的功能、結構和環境等協調統一.Mattoccia 等[36]利用Grasshopper/Rhino 軟件,對單層零厚度的三浦折疊結構進行了參數化建模,以便利用幾何參數控制最終的折紙構型.Curlettod 和Gambarotta[37]考慮了相鄰模塊運動兼容性條件,建立了基于Waterbomb折痕圖案的參數化模型,通過給定角度來獲得不同折展狀態下的折紙模型.Wonoto 等[38]綜合采用數字化設計和有限元分析工具,分析了可展開折紙的幾何特性,探討了將微觀結構的幾何和機械原理用于建筑元素的可能性.此外,部分學者提出了可用于折紙構型初步設計的計算程序或插件[25-26,35,39].

然而,已有方法往往更側重如何將二維紙張按特定折痕轉化為三維構型,且已有的參數化模型大多為單層、零厚度折紙模型.如何依據特征幾何參數快速、準確生成多層堆疊的復雜三維模型、尤其是非零厚度實體模型,如何根據結構實際需求實現科學合理的結構逆向設計,仍是折紙結構數字化設計亟待解決的難題.為此,本文擬基于三浦折紙胞元以及超材料的構成規律,綜合利用Matlab 和Grasshopper 軟件,搭建折紙超材料結構數字化設計平臺,深入探索折痕總長、相對密度、折疊率等指標的演變規律,并輔以部分3D 打印物理模型及有限元分析模型進行驗證分析,以實現零厚度及非零厚度復雜折紙結構模型的高效、一體化建模,同時可為該類折紙結構的力學性能模擬、試驗研究及工程應用等奠定較好的基礎.

1 幾何構型

圖1(a)所示為三浦折紙基本胞元的半折疊構型,單個胞元由四個平行四邊形組成.其實,胞元的幾何構型可通過多種方式參數化,這里采用的是兩個靜態折痕長度a，b以及一個靜態內角 γ 定義折疊模式,同時用四邊形平面與XY平面的二面角 θ 來量化折疊程度[30].令X和Y為結構平面內坐標,Z為面外坐標,則結構幾何構型可由以下尺寸參數確定

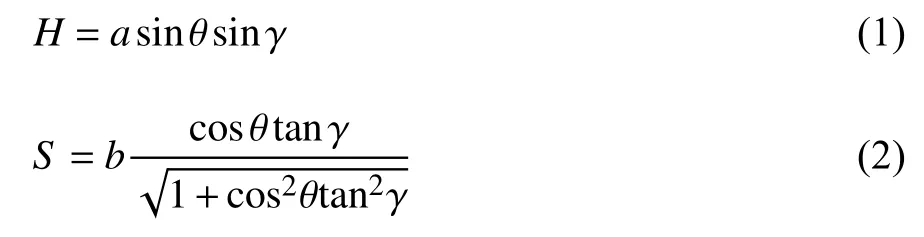
圖1 折紙超材料結構模型Fig.1 An origami metamaterial structural model

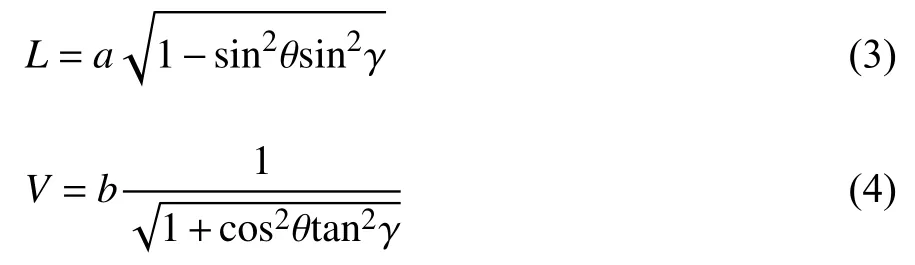
式中，H為結構沿Z向高度,2S為結構沿X向的長度,2L+V為結構沿Y向長度.將上述胞元按照M×N(圖1(b)中M=N=5)的排列模式拼接成三浦折疊薄殼結構,其中M和N分別為X向和Y向胞元個數.部分折疊的三浦折疊薄板可視為薄殼結構,值得指出的是,折疊模式可有效改變薄殼結構的整體力學性質(例如負泊松比).

根據三浦折紙基本單元的幾何構型,可發現胞元在X和Y兩個方向膨脹的耦合僅取決于邊長b與Y軸的夾角.因此,具有不同高度H的三浦折疊薄殼可以堆疊在一起,并沿著折疊線粘合起來,同時保持自由折疊的特性,其結果即圖1(c)所示的三浦折疊超材料.假設三浦折疊殼在堆疊時按照ABABAB的模式,在Z向重復堆疊O組,為了確保A和B層薄殼在折展過程中的幾何協調性,兩層薄殼的幾何構型需滿足:SA=SB,VA=VB,LA=LB,且HB≥HA(即γB≥γA).因此,B層薄殼相對應的幾何參數需滿足

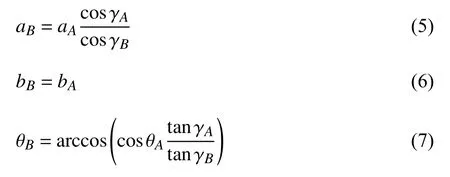
由上可知,三浦折疊超材料的主要幾何參數為面板厚度h,A層薄殼面板面內角γA,B層薄殼面板面內角γB,A層薄殼面板傾角θB∈[0,π/2],A層薄殼面板邊長aA和A層薄殼面板邊長bA.圖1(c)所示M×N×O=5×5×6 的超材料模型作為結構標準模型.

2 結構構型的數字化設計

2.1 Rhinoceros 幾何參數建模

傳統建模或找形方法難以生成復雜的三維折紙結構模型,且參數分析時往往需要大量、重復性的建模與調整,工作量巨大.另一方面,如何根據折紙結構的實際需求合理完成結構的逆向設計,亟待解決.為此,本文利用犀牛及其可視化編程插件Grasshopper,實現了三浦折紙超材料結構數字化快速建模,為復雜折紙結構的正向與逆向設計搭建橋梁.結合軟件內置電池實現特定的幾何建模,將建模過程轉化為有邏輯性的模塊連接,參數化面板的部分樹形結構如圖2 所示.

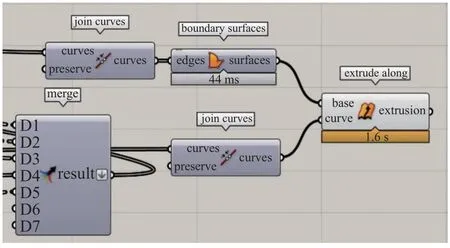
圖2 Grasshopper 參數化面板Fig.2 Grasshopper parametric panel

需指出,三維實體模型便于結構的3D 打印及精細化有限元分析等,往往可通過中間層的面偏移方式構建.然而,三浦折紙超材料模型每個基本單元均是由不同角度的空間面板組成,面偏移的方式會使得不同角度的面板與相鄰面板發生交融或空缺,需進行大量的修剪和填補工作.為避免該問題,選用結構側截面沿指定路徑擠出的方式建立三維實體.

盡管上文幾何構型分析確定了結構的五個主要參數,但并不便于直接建模.如圖3 所示,結構數字化建模需通過幾何推導,求得XZ平面上基本單元的參數和XY平面上擠出路徑的參數.隨后,通過已確定的M,N,O數值與實體模型厚度參數h生成XZ平面上的基準面與XY平面上的路徑.最后,將基準面沿著路徑擠出得到實體模型.幾何關系如下

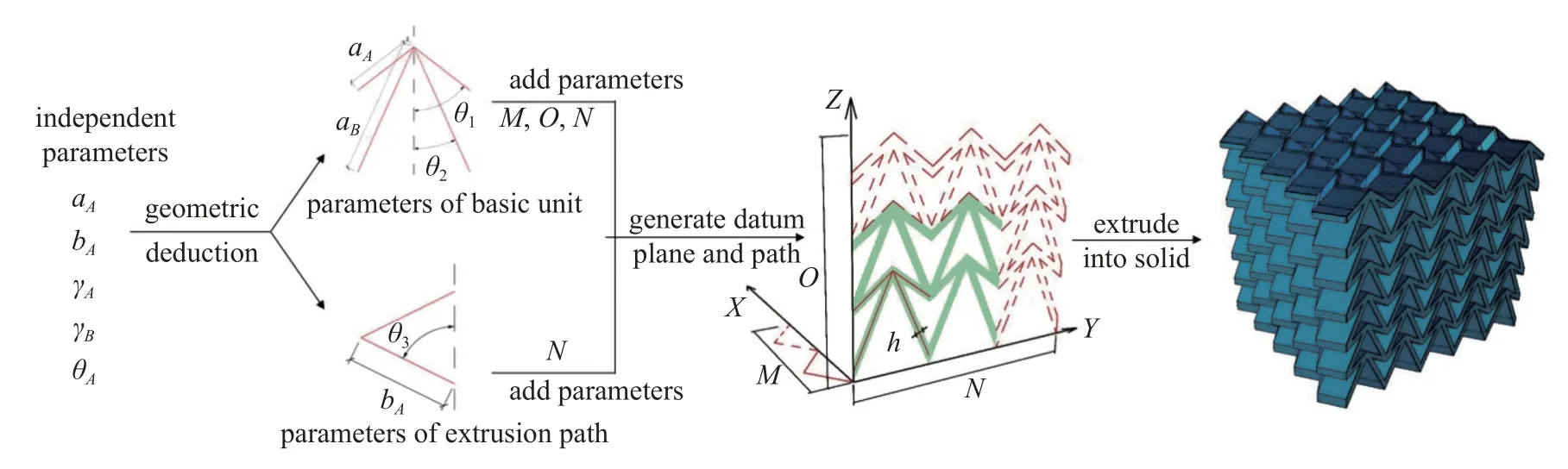
圖3 數字化建模流程Fig.3 Digital modeling process

其中fA和fB分別為aA和aB的單側偏移長度.

該過程實現了僅需輸入5 個獨立參數、3 個方向的堆疊個數和模型厚度共9 個參數,便能便捷地實現折紙超材料結構的數字化建模.值得注意的是,該方法實現了零厚度折紙超材料模型與非零厚度三維實體模型的統一建模,當各層折紙面板厚度參數取為零值時,實體結構即降階為等效的三維薄殼模型.

2.2 物理模型驗證

為驗證參數化建模的可行性及精確性,對三浦折紙超材料結構進行了物理模型驗證.3D 打印技術是一種以數字模型文件為基礎,通過材料的空間堆疊而快速實現實體化的技術,現廣泛應用于汽車、航空航天、微機電系統、生物醫療等領域.熔融沉積法(FDM)是眾多3D 打印方法中使用最廣泛的,通過加熱噴嘴融化線材,沉積于工作區域并固化成型,由數字模型文件控制分層工作區域.FDM 型3D 打印機可打印熱塑型聚氨酯(TPU)、聚乳酸(PLA)、聚苯乙烯等材料.

本文采用熔融沉積法,選用PLA,Agilus30 樹脂以及TPU 材料,打印制作了6 個實物模型(圖4),對上述三浦折紙超材料結構進行物理模型驗證(模型參數見表1),其中γA=60°,γB=75°.

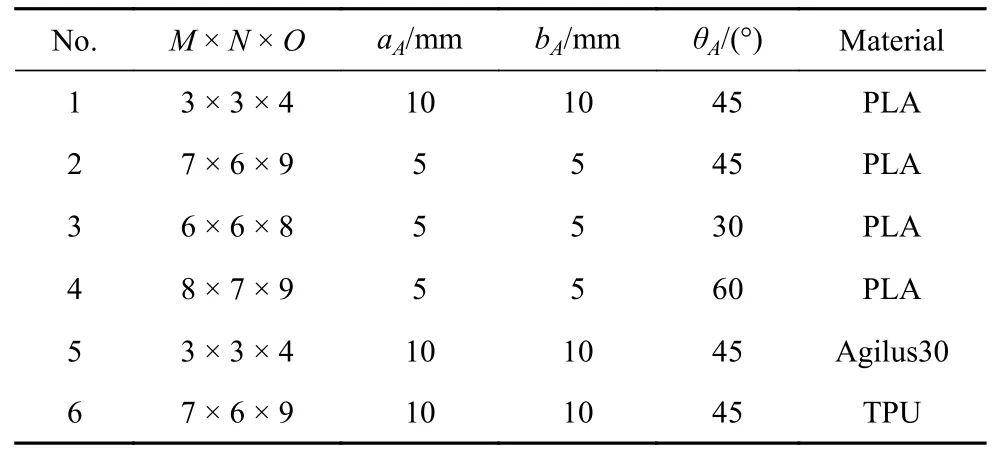
表1 3D 打印實物模型參數Table 1 Parameters for physical models by 3D printing

由圖4 可知,盡管構型復雜、單元厚度極薄,3D 實物模型可精確打印,結構壁厚均勻、表面光滑,完成度極高.模型用料量、面板尺寸及壁厚均與數字化模型高度吻合(相對誤差小于0.5%),因此驗證了折紙結構數字化、參數化建模的準確性.值得一提的是,與圖4(a)結構相比,圖4(e)模型選用更柔的Agilus30 樹脂材料3D 打印而成、其他參數不變,由于Agilus30 樹脂具備較理想的變形能力,該結構可反復、平順地從展開狀態壓縮至緊湊的折疊狀態,反之亦然.

圖4 三浦折疊超材料結構模型驗證Fig.4 3D printing and digital Miura-ori metamaterial structural models

3D 打印技術和FDM 操作方便,設備成熟度高,可選用的材料較為豐富,折紙超材料構型復雜,相比傳統結構加工方法成本高且耗時長,更適合采用3D 打印技術.此外,使用的多為塑料質材料,模型的表面光滑,不需要后續處理,有利于折紙超材料結構的后續研究.誠然,3D 打印制作折紙超材料結構仍存在一定的局限性,例如結構力學性能有待進一步研究、加工時長及成本較高、材料選型有限等.

3 幾何特性與結構選型

3.1 幾何特性

3.1.1 折痕長度

不失一般性,令三浦折紙超材料結構的三向胞元個數為M×N×O,共包含有4M×N×O個平行四邊形面板,面板之間通過公共邊(折痕)相連.近期研究已表明[5,40-41],多折痕折紙管在折展變形時,折痕處應變明顯高于面板且吸收了大部分能量.可知,折痕總長度不僅影響結構的吸能性能,而且影響實際構件的制作難度與成本.因此,需對不同幾何參數下結構折痕總長進行對比分析.

折痕總長度由以下兩部分組成:兩個平行四邊形面板之間的連接處折痕長度L1和四個平行四邊形面板之間的連接折痕長度L2,其中L2存在于AB兩個單層薄殼的連接處.推導了折痕長度的解析表達

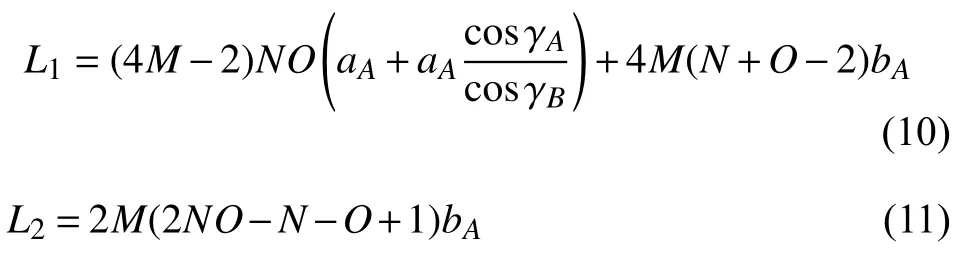
由式(10)可見,L1隨著平行四邊形面板邊長aA和bA的增大而增大;由式(11)可見,L1與bA線性相關.針對標準模型,取aA=10 mm,bA=10 mm代入式(10)和式(11)得

折痕長度L1與γA及γB的關系如圖5 所示,可以發現,在其他條件相同的情況下,L1隨著γA的增大而減小.對于不同的γB,L1的最小值均相等,數值為12.6 m,且只有在γA=γB時L1達到最小值,這一點在L1的表達式(10)中可得到驗證.

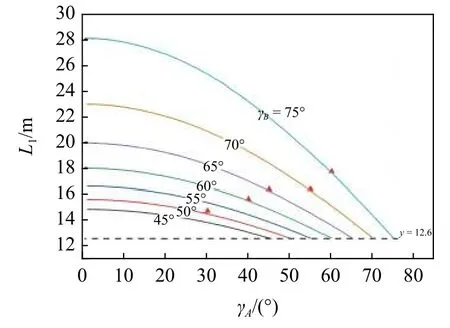
圖5 不同γB 情況下L1 與γA 的關系曲線 (M=N=5)Fig.5 Change curve of L1 with γA under different γB conditions(M=N=5)

3.1.2 相對密度

三浦折紙超材料結構應用于緩沖吸能時,不僅需要評估結構吸能的能力,同時要考慮結構的相對密度大小,相對密度較小卻擁有較好的吸能能力是性能優異吸能材料的優勢,同時可以降低材料的制作成本[5,27].推導了X,Y,Z向堆疊數量為M,N,O的一般模型的相對密度,解析表達如下

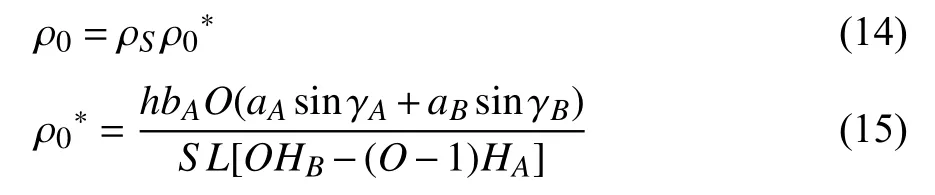
式中，ρ0為材料密度,ρS和ρ0*分別是基材的密度和超材料的相對密度.

將式(1)～式(4)代入式(15)可得

當O值較大時,該式可簡化為

根據式(14)可知,對于給定的銳角γA和γB、邊長bA和四邊形平面與XY平面之間的二面角θA,相對密度h/a成正比,且不受邊長bA的影響.針對γA,γB和θA對模型相對密度的影響,選取標準模型具體分析,其中aA=10 mm,bA=10 mm,θA=45°,h=0.3 mm.根據式(16)求得標準模型的相對密度

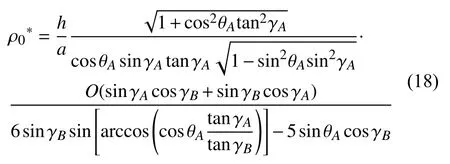
圖6(a)描繪了標準模型的相對密度在不同γA和γB組合下的變化情況,可以發現γB保持不變時,相對密度隨著γA的增大先減小后增大.每條密度曲線均存在有一個最小值,且隨著γB的減小,最小密度所對應的γA相應地減小.θA同樣會影響超材料的相對密度,由圖6(b)可知,ρ0*隨著θA的增大而增大,且增速逐漸變大.

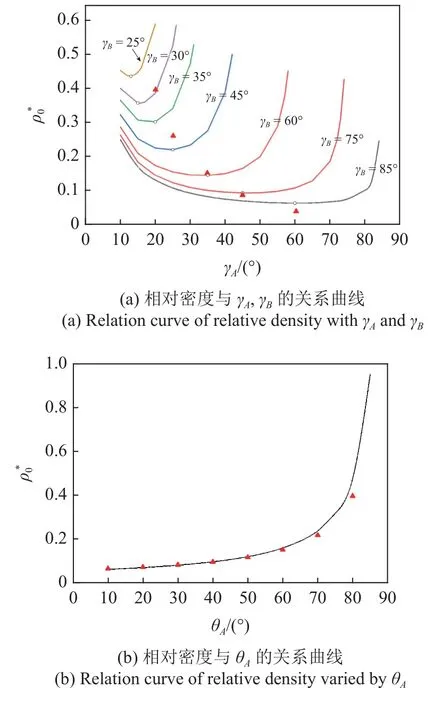
圖6 相對密度理論曲線Fig.6 Theoretical curve for relative density

3.1.3 折疊率

折疊率是可展結構、折紙結構的重要指標之一,可體現結構的折展效率,一般采用結構折疊前所占面積、體積與折疊后所占面積、體積的比例來具體描述.對于可展結構,折疊率越高則結構的折展效果越好[2,27],便于存儲、運輸;對于吸能耗能結構,高折疊率的結構往往具有更優異、充分的形變空間和塑性變形,因此往往能耗散更多的塑性應變能[40,42-44].

令模型的折疊率ζV為結構完全展開至圖7(自鎖)時的體積與完全壓縮態下的體積比,三向堆疊數M×N×O的一般模型的折疊率計算如下

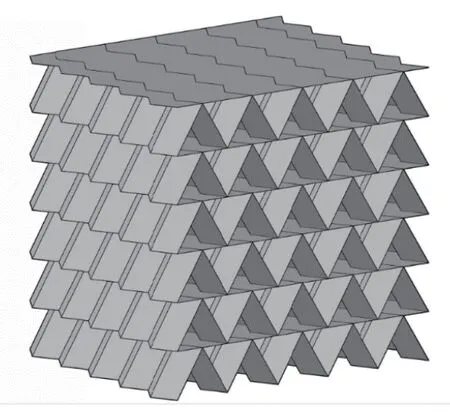
圖7 標準模型沿X 方向完全展開構型Fig.7 Fully deployed configuration of reference model along direction X

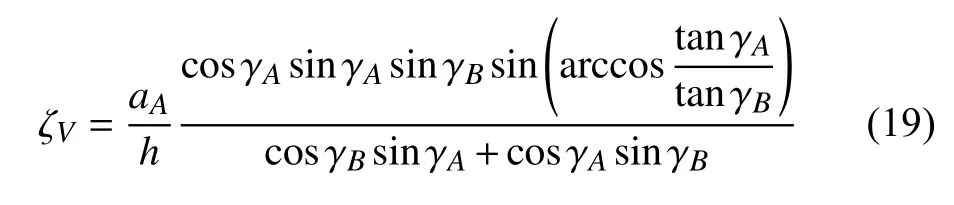
由式(19)可知,折疊率僅與aA,h,γA,γB相關,與aA/h成正比例.例如,取aA=10 mm,h=0.3 mm,可獲得折疊率隨角度γA和γB的演變規律,如圖8所示.

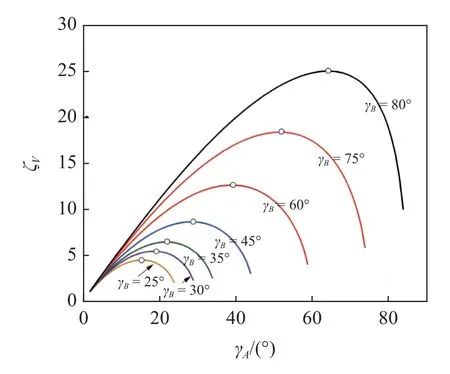
圖8 折疊率ζV 與γA 及γB 的關系曲線Fig.8 Relation curve of maximum folding ratio ζV with γA and γB

可以發現,γB保持不變時,ζV隨著γA的增大先增大后減小.每條折疊率曲線存在一個最大值,γB越大的曲線對應的折疊率最大值越大,且隨著γB的增大,最大值所對應的γA相應地增大.

3.2 數字化設計誤差分析

為進一步驗證本文數字化設計方案的正確性,將其更準確地應用于三浦折紙超材料結構的選型優化,本節結合幾何特性的理論推導進行驗證.

為驗證所推導折痕長度的準確性,分別選取圖5 中γA=30°,γB=50°;γA=40°,γB=60°;γA=45°,γB=65°;γA=55°,γB=70°;γA=60°,γB=75°五組模型數據,利用數字化建模技術建立三維模型,并求得對應實體模型的折痕長度L1,如圖5 中的散點數據所示.對比可發現,L1理論值與實體模型中的長度吻合較好,相對誤差分別為1.64%,1.00%,0.82%,0.79%,0.64%.

為了驗證所推導相對密度的準確性,分別選取γB=35°,γB=45°,γB=60°,γB=75°,γB=85°五組相對密度曲線上的理論最低值點,利用數字化建模技術建立一系列三維模型,并求取對應實物模型的相對密度,即圖6(a)中的散點.求得相對誤差分別為23.9%,16.01%,5.05%,-8.29%,2.76%,圖9 為其中部分三維數字化模型示意.由于γA,γB較小時相鄰面板間夾角較小,實體模型需要填補的空缺體積較大,因而相對誤差較大,其余幾組與理論值吻合較好.

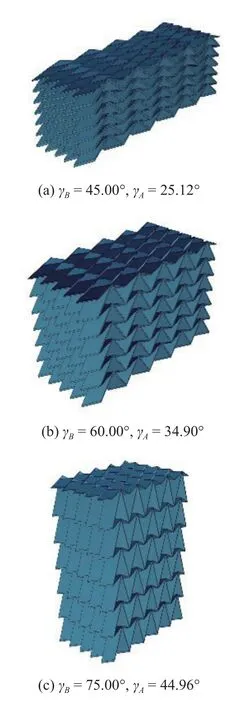
圖9 不同γA 的部分三維模型示意Fig.9 3D models with different γA

此外,為進一步驗證推導所得相對密度與θA的變化關系,選取圖6(b)中θA=20°,θA=30°,θA=50°,θA=70°,θA=80°五組參數建立實體模型,見圖10,求得對應的相對密度值,即圖6(b)中散點.求得的相對誤差分別為3.15%,1.67%,-2.55%,-9.39%,-20.00%.

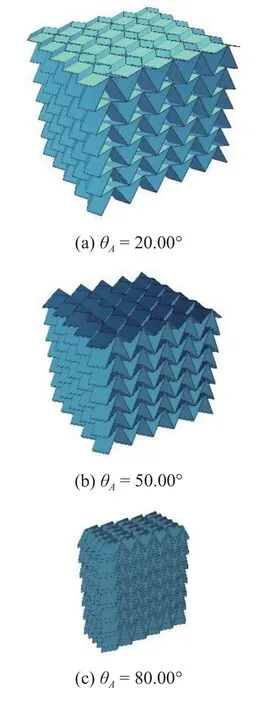
圖10 不同θA 的部分三維模型示意Fig.10 3D models with different θA

3.3 準靜態壓縮過程分析

由于折紙結構輕質節材、耗能優異等特點,常作為薄壁吸能耗能結構應用于諸多領域[42-44].為揭示相對密度對三浦折紙超材料結構吸能效率的影響規律,利用Abaqus/Explicit 對其進行準靜態壓縮過程分析與驗證.將超材料結構放置在一個固定的剛性平面和一個可在壓縮方向移動的剛性平面之間.結構自身選通用接觸,摩擦系數為0.3,與剛性面板之間設置點面耦合.設置位移荷載,其值為結構壓縮方向長度的70%,并設置平滑分析步以保證收斂性.超材料結構網格類型選用S4 R 積分四邊形單元,尺寸選為3,剛性面板選用R3D4 單元.令計算結果中動能與內能之比小于5%,以保證動力效應可忽略不計;偽應變能與內能之比小于10%,以避免沙漏效應對結果帶來的影響.

由式(12)、式(13)和式(17)可知,自變量θA的變化不引起折痕長度的變化,但會使相對密度發生改變.選用標準模型,取γA=60°,γB=75°,aA=aB=10 mm,h=0.3 mm,模型參數如表2 所示.材料均選用6061-T6 鋁合金,密度2750 kg/m3,彈性模量70 GPa,泊松比0.3,屈服極限300 MPa.

例如,圖11(a)描述了其中模型Mi-3 的壓縮變形過程,當該結構模型受圖1(a)所示X軸方向的軸向壓縮作用時,X向產生顯著的壓縮變形,同時沿Y和Z向收縮,結構呈現出顯著的負泊松比效應.

五組模型的力位移曲線如圖11(b)所示,這里引進一個能更好體現結構輕量化的指標SEA (specific energy absorption)[40,43-44],即單位質量的吸能能力,其計算方法如下

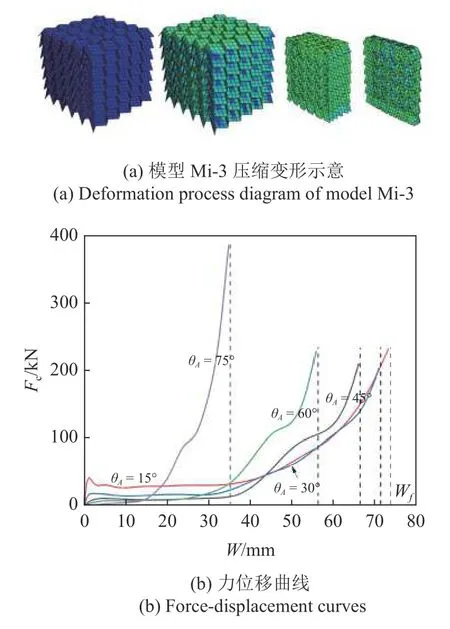
圖11 三浦折紙超材料結構壓縮性能分析Fig.11 FEM results for Miura-ori metamaterial structures under quasistatic compressions

其中，E為壓縮過程中吸收的總能量,m為模型質量.計算結果見表2.

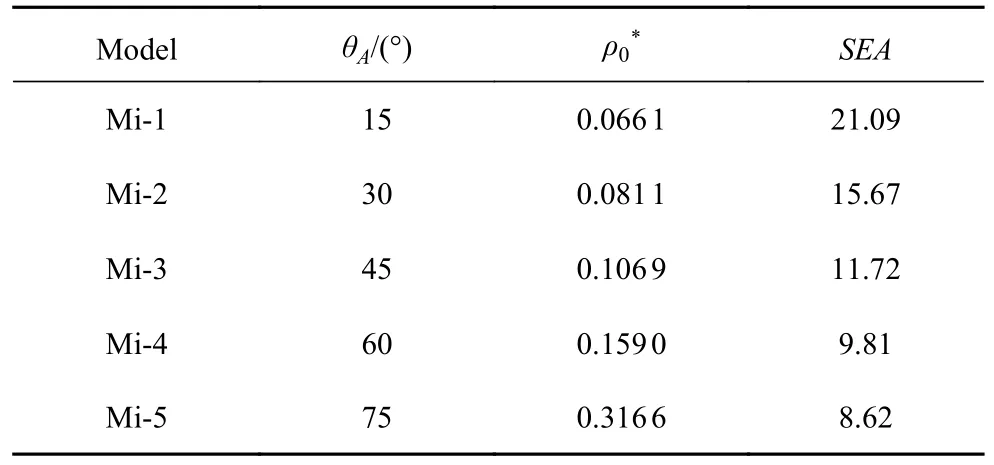
表2 模型參數與模擬結果Table 2 Parameters and FEM results for different models

由表中數據可知,A 層面板傾角θA的增大不改變模型的質量,相對密度增大,SEA反而減小,即模型的吸能效率降低,同時由式(11)和式(12)可知此時模型的折痕長度不發生變化.可知在A 和B 層胞元面板構型、折痕總長度及面板厚度不變的前提下,三浦折紙超材料結構的相對密度與比吸能成反比關系.因此,結構選型時,可根據圖6 選取相對密度較小的變量組合.

4 結論

本文基于三浦折疊胞元以及三浦折紙超材料的幾何構型,給出了決定構型的幾何參數,對工程應用中較為關注的超材料結構折痕總長、相對密度及折疊率等指標,系統推導了一般模型的理論表達式,并揭示了以上特性與三浦折紙超材料結構幾何參數的演變規律.選定標準模型,探究得γA=γB時折痕總長L1最短,折痕總長L2的大小僅與B 層胞元邊長bA有關,可根據結構需求取折痕長度的參數組合;分析求得使三浦折紙超材料結構折疊率達到峰值的面內角γA和γB組合;由系列模型的準靜態壓縮分析結果可知,當結構面板構型及折痕總長不變時,較小的結構相對密度可顯著提高吸能效率,構型選擇時應尋求相對密度較小的參數組合,從而降低質量和成本、提高吸能效率.上述結論對不同性能需求下結構幾何參數選取具有指導意義,有利于折紙結構的正向、逆向設計.

利用Matlab 和Grasshopper 實現了零厚度及非零厚度折紙超材料模型的數字化設計.對比折痕長度、相對密度的理論值與實體模型計算值,驗證了數字化建模的正確性,為部分超材料結構的參數化建模提供了可行思路,也為三浦折紙超材料結構的后續研究提供了極大便利.

此外,利用3D 打印技術開展了物理模型驗證,3D 打印折紙模型可實現模型流程化與標準化建造、降低制作工效與成本,再次驗證了數字化建模的正確性,是將3D 打印技術應用于折紙結構智能建造的一項重要實踐,對后續折紙研究亦有參考價值.