基于交點參數的任意多邊形窗口對圓裁剪①

李曉武, 陳 平

(北京科技大學 機械工程學院, 北京 100083)

裁剪是計算機圖形學的基本問題之一, 也是CAD軟件系統的一個重要圖形編輯功能, 裁剪一般是指把一個封閉區域作為裁剪窗口, 去裁剪其他圖形, 把其他圖形中不在窗口內的部分裁剪掉, 只保留窗口內的部分. 裁剪功能除了在CAD軟件中大量使用外, 在計算機動畫、機器人運動學仿真、建筑設計、地理信息系統、平面繪畫、影視特技圖像處理以及模式識別等領域都有廣泛應用.

目前, 裁剪算法的研究主要集中在多邊形裁剪方面, 裁剪算法比較豐富, 有適合矩形裁剪窗口的逐邊裁剪法、Liang-Barsky算法、中點分割算法, 適合凸多邊形裁剪窗口的線裁剪Cyrus-Beck 算法、Sutherland-Hodgman算法、外接矩形判別法和分區判斷直接裁剪法以及適合任意多邊形裁剪窗口的Weiler-Atherton雙邊裁剪算法等[1–13].

圓裁剪也是一個重要的圖形裁剪功能, 具有廣泛的應用, 圓裁剪有兩種類型, 一是圓做裁剪窗口對各種圖形進行裁剪, 例如圓窗口對直線段的裁剪[14–18], 二是多邊形或者其他圖形作為裁剪窗口對圓進行裁剪, 裁剪后只保留窗口內的圓弧部分. 在第二種圓裁剪類型中, 矩形窗口的圓裁剪在視窗顯示時應用較多, 裁剪算法有逐邊裁剪法、區域編碼法及投影法等[19–22]. 除了矩形窗口的圓裁剪外, 在實際應用中, 也存在任意多邊形做裁剪窗口的圓裁剪情況, 因此, 研究任意多邊形窗口的圓裁剪也具有重要的實用價值. 關于多邊形做裁剪窗口的圓裁剪, 文獻[23]提出了一種方法: 首先, 計算多邊形每條邊與圓的交點, 再對交點在圓周方向排序, 然后再進一步判斷相鄰交點間的圓弧是否在窗口內, 該方法為多邊形窗口的圓裁剪提供了一條有效的途徑, 但是, 文獻中的算法需要開平方計算交點和反三角計算檢測圓弧的可見性, 效率低且耗資源; 文獻[24]將圓裁剪分成相交性檢測求交點、點在多邊形內外判斷、交點排序以及可見性檢測等5個步驟, 在圓與多邊形相交性檢測時利用投影和射線法相結合, 降低了運算的耗費, 對交點排序和圓弧可見性檢測方法也做了相應改進, 算法的效率相比文獻[23]有所提高. 文獻[25]提出了和文獻[24]類似的方法, 利用X-掃描線法分析圓與多邊形的位置關系, 再利用多邊形頂點與圓的相對位置對交點排序. 文獻中提出的方法, 除了細節不同外, 算法的整體思路基本上是相同的: 均是先求出多邊形與圓的交點, 再對交點在圓矢量方向上排序,然后, 判斷相鄰兩個交點之間的圓弧段是否在多邊形裁剪窗口內(即可見性檢測), 從而實現對圓的裁剪. 在上述思路中, 除了計算交點外, 交點排序和相鄰交點之間圓弧的可見性檢測也是非常重要的環節, 文獻采用的交點排序方法有三三排序法[24]、比較頂點和圓心距離的排序法[25]等, 但是, 這些排序方法只適用于多邊形裁剪窗口只有外環的情況, 當多邊形裁剪窗口除了外環外還含有一個或多個內環多邊形時, 文獻中的交點排序方法就會出錯, 則后續的圓弧可見性檢測方法也會失效, 因此, 文獻中的方法不適合有內環的任意多邊形做裁剪窗口的圓裁剪情況.

筆者在進行相關課題研究時, 對任意多邊形裁剪窗口的圓裁剪問題也進行了探討. 通過分析發現, 當多邊形裁剪窗口和圓相交時, 利用交點相對裁剪窗口的進出點特性, 即可判斷圓弧段的可見性, 不需要再對圓弧的可見性單獨進行檢測, 而通過比較圓與多邊形邊所在直線相交的參數值大小就能夠直接確定交點的進出點特性信息, 也不再需要其他額外的計算判斷.

為此, 本文提出了一種基于交點參數值分析的任意多邊形裁剪窗口的圓裁剪算法, 與文獻中的方法相比, 本算法只需對交點參數值進行比較, 即可判斷出裁剪窗口內的圓弧部分, 判斷步驟簡潔明了, 效率要明顯高于文獻中的方法, 適用于包括含內環多邊形在內的任意多邊形做裁剪窗口對圓進行裁剪的情況.

1 基于進出點特性的多邊形窗口對圓裁剪

在任意多邊形裁剪窗口對多邊形的裁剪算法中, 基于交點進出點特性的Weiler- Atherton雙邊裁剪算法是一種非常有效的解決方案, 該方法通過將兩個多邊形設置為有向多邊形, 當兩個多邊形有交點時, 沿著多邊形的方向, 通過判斷交點是進入裁剪窗口的進點還是離開裁剪窗口的出點, 并保留進點和出點之間的多邊形,實現裁剪. 該方法利用交點的進出點特性獲得裁剪窗口內的部分, 對多邊形裁剪窗口的圓裁剪具有借鑒意義.

圖1所示為一個多邊形裁剪窗口對圓裁剪, 其中,多邊形為P0P1P2P3P4P5P6P7P8, 順時針走向,O是被裁剪圓, 逆時針走向. 圓O與多邊形相交的交點為:I0、I1、I2、I3、I4和I5. 根據交點的進出點分析方法, 沿著圓的走向, 進入多邊形裁剪窗口內的交點稱為進點, 離開多邊形裁剪窗口內的交點稱為出點, 由于圓本身是封閉的, 裁剪窗口的內部區域也是連通的, 所以, 進點和出點成對出現, 數量相同. 沿著圓的走向, 從進點到出點之間的圓弧位于多邊形裁剪窗口內部, 在裁剪時應予以保留, 從出點到進點之間的圓弧在多邊形裁剪窗口的外部, 應裁剪掉. 因此, 在求出多邊形裁剪窗口和圓的交點后, 首先, 沿著圓的走向對交點進行排序,然后, 對排序后的交點, 進行進點? 出點的組合, 這樣,就可以獲得多邊形裁剪窗口內部的圓弧. 例如, 圖1中,將多邊形裁剪窗口和圓的交點沿著圓的逆時針走向排序, 順序 為:I0(進點)?I5(出點)?I4(進點)?I3(出點) ?I2(進點)?I1(出點), 則進點? 出點的組合為:I0?I5、I4?I3和I2?I1, 對應這些進點到出點之間的圓弧為裁剪后需保留的部分.

圖1中的多邊形裁剪窗口是只有一個外環的一般多邊形的情況. 下面對形狀更為復雜的含內環的任意多邊形裁剪窗口的圓裁剪情況進行分析.

圖1 多邊形窗口的圓裁剪進出交點分析

圖2為一個含內環的多邊形對圓進行裁剪, 多邊形的外環頂點依次為P0P1P2P3P4P5P6, 外環按順時針走向, 內環頂點依次為Q0Q1Q2Q3Q4, 內環按逆時針走向,O是被裁剪圓, 逆時針走向. 圓O分別與多邊形裁剪窗口的內外環相交, 圓與外環的交點以及交點的進出點特性為:I0(進點)、I3(出點)、I2(進點)和I1(出點),圓與內環的交點以及交點的進出點特性為:I4(出點)和I5(進點). 沿著圓的逆時針走向, 對所有交點進行排序, 順序為:I0(進 點)?I4(出 點)?I5(進 點)?I3(出點) ?I2(進點)?I1( 出點). 則排序后的交點進行進點?出點組合為:I0?I4、I5?I3和I2?I1, 對應這些進點到出點之間的圓弧也為裁剪后需保留的部分.

圖2 含內環的任意多邊形裁剪窗口的圓裁剪

因此, 利用交點的進出點特性也可以實現對含內環多邊形在內的任意多邊形裁剪窗口的圓裁剪.

本裁剪算法的步驟歸納如下:

第1步. 依次判斷多邊形外環和內環的每條邊與圓是否相交, 如相交, 則計算交點;

第2步. 判斷交點是進點還是出點, 并在交點信息中記錄其進出點特性;

第3步. 沿圓的走向將交點進行排序;

第4步. 根據交點的進出點特性, 將排序后的交點進行進點? 出點組合, 保留進點? 出點之間對應的圓弧.

2 交點進出點特性和直線參數的關系

在上述的裁剪算法中, 判斷交點的進出點特性是整個算法的關鍵. 對于多邊形裁剪窗口對多邊形的裁剪, 可以通過被裁剪邊的兩個頂點和裁剪邊的相對位置關系來判斷交點是進點還是出點, 但是對于圓裁剪,由于圓本身沒有頂點, 所以, 不能再借鑒多邊形的進出點判斷法來分析圓與多邊形交點的進出點特性, 因此,還需要尋找新的方法來判斷交點的進出點信息.

設線段P0P1是多邊形裁剪窗口的一條邊, 兩個端點分別為P0(x0,y0) 和P1(x1,y1) , 邊的方向是P0指 向P1,則該邊所在直線的參數方程表示為:

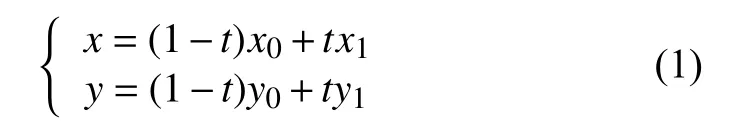
如圖3所示, 參數將邊所在直線劃分為3個區域:(-∞,0)、 [ 0,1]和 ( 1,+∞), 其中, 當參數值t∈[0,1]時, 對應直線上的點在P0和P1之間的線段上, 即在多邊形的邊上, 而且參數值從P0到P1逐 漸增大; 當t?[0,1]時, 對應直線上點不在P0和P1之間的線段上, 而是在該線段兩側的延長線上; 當t＜0 時, 點在P1指 向P0的線段延長線上,t值越來越小, 當t＞1時 , 點在P0指 向P1的線段延長線上,t值越來越大, 也即直線上的點在沿著P0指 向P1的方向上, 對應的參數值t越來越大, 反之, 參數值t越來越小.

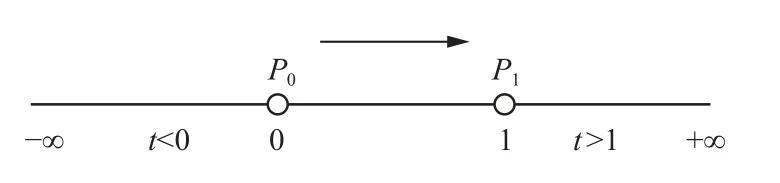
圖3 邊所在直線的參數表示

設多邊形為有向多邊形, 其中, 外環為順時針走向,內環為逆時針走向, 則多邊形內部所在區域具有這樣的特點: 不管是外環邊還是內環邊, 沿著邊的走向前進,即沿著P0點 指向P1點的方向前進, 這時, 邊的右側均為多邊形的內側區域. 即使多邊形的各邊具有不同的傾斜方向, 該特點仍然存在, 如圖4所示.

圖5所示是多邊形的一個邊所在直線與圓相交的情況, 圓的走向是逆時針, 邊直線的方向是P0點指向P1點, 則沿著直線走向的右側是多邊形的內側區域. 若圓與直線P0P1相 交, 交點記為I0和I1, 則從圖中可以看到, 圓在交點I0處進入多邊形內側區域, 即I0為進點, 在交點I1處 離開多邊形內側區域, 即I1為 出點, 設交點I0和I1在 直線的參數方程式(1)中對應的參數值分別為t0和t1, 這時, 參數值t0和t1的大小關系是:

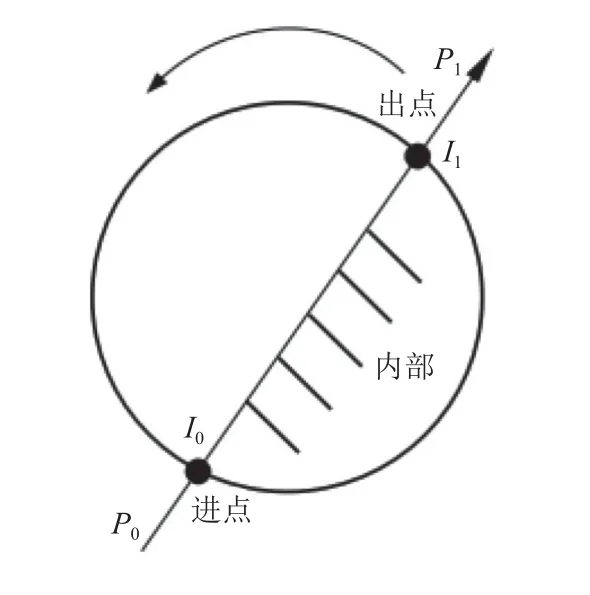
圖5 有向邊直線和圓相交

式(2)也是圖4中有向邊所在直線第一種傾斜情況下, 和圓相交時交點的進出點特性和交點在直線上參數值大小的對應關系.

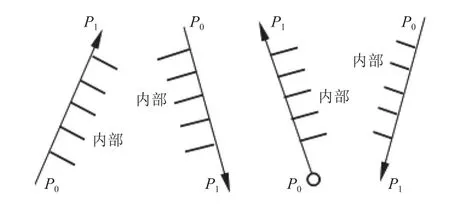
圖4 有向邊的右側為多邊形內側區域

圖6是圖4中有向邊所在直線的另外3種傾斜方向下和逆時針走向圓相交的情況, 直線的方向是P0點指向P1點 ,I0和I1是 兩個交點, 其中,I0為進點,I1為出點,從圖6也可以得出和圖5相同的結論: 沿著邊所在直線的走向, 如果右側是多邊形裁剪窗口的內側區域, 圓沿逆時針走向, 圓和直線相交的兩個交點分別是進點和出點, 則進點在直線上的參數值小于出點在直線上的參數值, 即進點和出點在直線上的參數值具有和式(2)相同的大小關系.

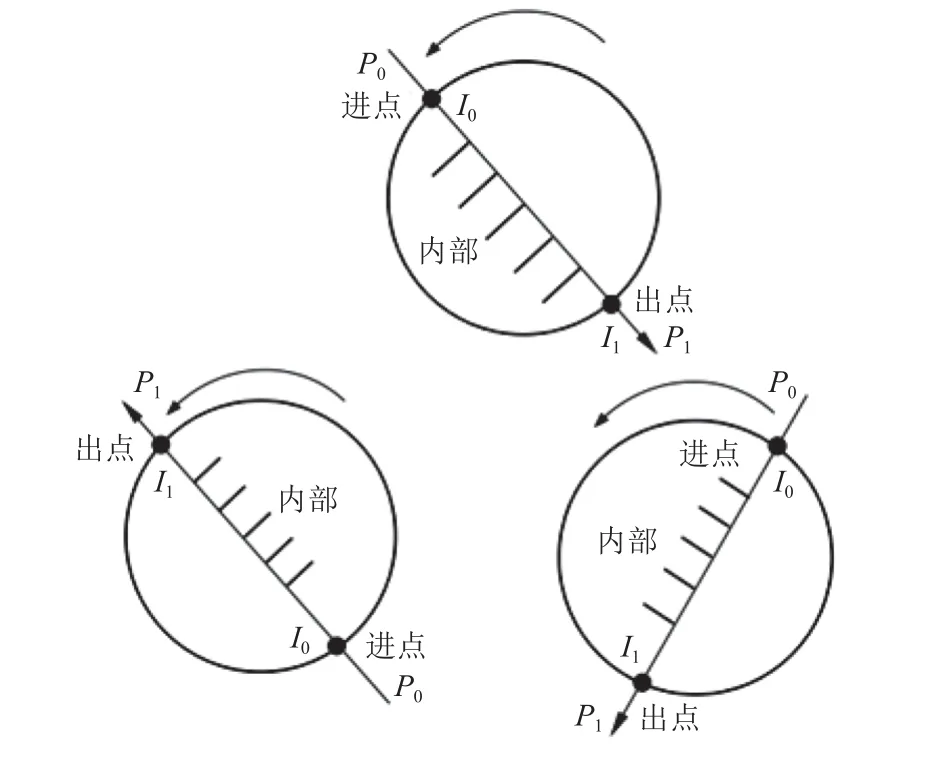
圖6 各種傾斜位置有向邊直線和圓相交

因此, 圓和多邊形裁剪窗口相交時交點的進出點特性, 通過判斷交點在對應邊所在直線的參數值大小即可確定下來, 這樣, 就利用第1節提出的基于交點進出點特性的多邊形窗口的圓裁剪算法, 即可實現對圓的裁剪.

3 圓與邊所在直線的交點計算及處理

上述的圓與多邊形邊相交是指圓與多邊形邊所在直線相交, 這時, 交點可能在多邊形的邊上, 也可能在邊的延長線上. 只有落在多邊形的實際邊上而不是在其延長線上的交點才用于裁剪, 這個交點稱為實交點,在邊的延長線的交點稱為虛交點. 當邊與圓沒有實交點時, 圓和該邊不存在裁剪, 不必計算. 只有存在實交點時, 才計算交點的參數值, 并比較大小, 判斷該實交點是進點還是出點.

判斷直線與圓是否存在交點的方法如下:

設圓的半徑是R, 圓心為Pc(xc,yc), 逆時針方向, 圓方程為:

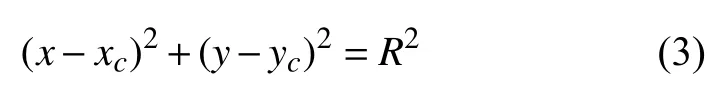
將式(1)中的直線參數化表示代入式(3)中, 建立參數t的一元二次方程. 該方程的解為:

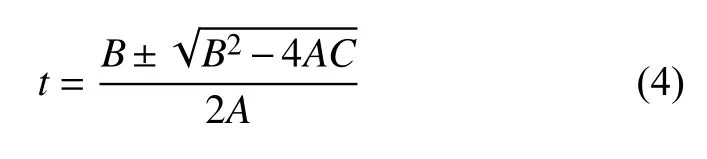
其中,

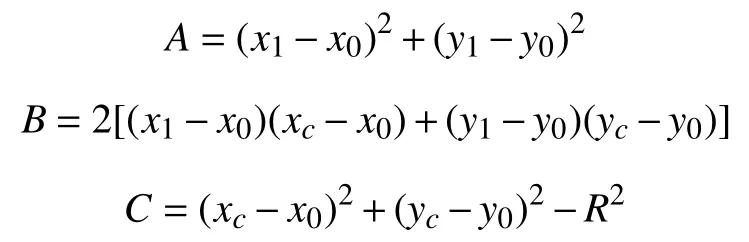
令Δ=B2-4AC, 則t=

當Δ ＜0時, 方程無解, 即直線和圓沒有交點.

當Δ =0時, 方程只有一個解, 即直線和圓相切, 此時也不必考慮裁剪.

當Δ ＞0時, 直線與圓有兩個交點, 這時需進一步判斷是否存在實交點, 當有實交點時, 計算方程的兩個解t1和t2:

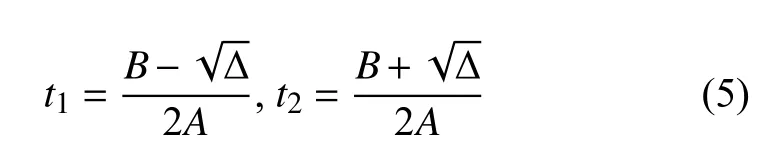
由于t1＜t2, 所以,t1對應的交點為圓在直線上的進點,t2對應的交點為圓在直線上的出點.

當0≤t1,t2≤1時 , 則t1和t2對應的兩個交點均為實交點, 將t1和t2代入式(1), 即得交點值, 將兩個交點插入交點序列中, 并標識每個交點的進出點特性.

當t1和t2中僅有一個值在[ 0,1] 區 間時, 則在[ 0,1]區間的t值對應的交點為實交點, 將該交點插入交點序列中, 并標識其進出點特性.

4 圓周方向交點排序

所有的實交點沿著圓周方向排序是實現裁剪的重要一步. 文獻中的交點排序方法是比較每個點在圓的逆時針方向對應的圓弧角大小, 需要進行反三角運算,比較耗性能. 由于所有的交點都在圓上, 所以, 本文采用比較交點與 (R,0) 或 者( -R,0)距離的方法進行排序,如圖7所示.

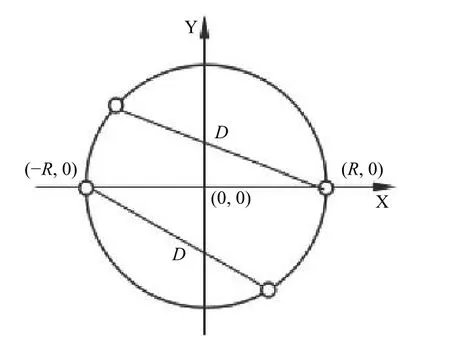
圖7 圓周方向交點排序

當交點的坐標值y≥0 (即交點在圓上0°到180°之間)時, 按交點到(R,0)的距離大小排序:

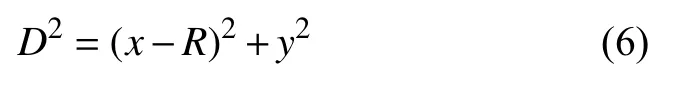
當交點坐標值y＜0 (即交點在圓上180°到360°之間)時, 按交點到圓上( -R,0) 的距離大小排序:

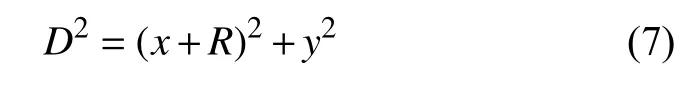
然后, 將兩組交點序列合在一起, 獲得所有交點的排序.

5 算法實例及與文獻算法的分析比較

為了驗證本文提出的基于交點參數的多邊形裁剪窗口的圓裁剪方法, 筆者在Visual C++平臺下進行了圖形編程, 在生成直線、圓、圓弧以及各種類型多邊形的基礎上, 實現了本文第1節提出的基于交點進出點特性的多邊形窗口的圓裁剪算法, 在算法中, 利用第3節的方法計算多邊形邊與圓的交點, 交點的進出點特性則根據第2節提出的交點所在邊直線的參數判斷,并按第4節的方法在圓周方向對交點進行排序.

圖8和圖9是利用本算法實現的裁剪效果實列,其中, 圖8是僅有外環多邊形裁剪窗口對圓的裁剪, 其中, 圖8(a)是裁剪前的多邊形裁剪窗口和被裁剪的圓,圖8(b)是裁剪后效果. 圖9是帶內環的多邊形裁剪窗口對圓的裁剪, 其中, 圖9(a)是裁剪前的多邊形裁剪窗口和被裁剪的圓, 圖9(b)是裁剪后效果. 圖8和圖9中的多邊形均通過隨機交互方式構造生成, 無任何特殊設定, 裁剪結果證實本文提出的算法是切實可行的.

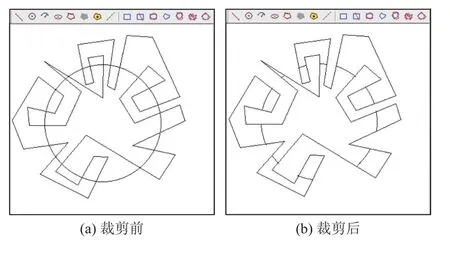
圖8 僅有外環的多邊形裁剪窗口的圓裁剪

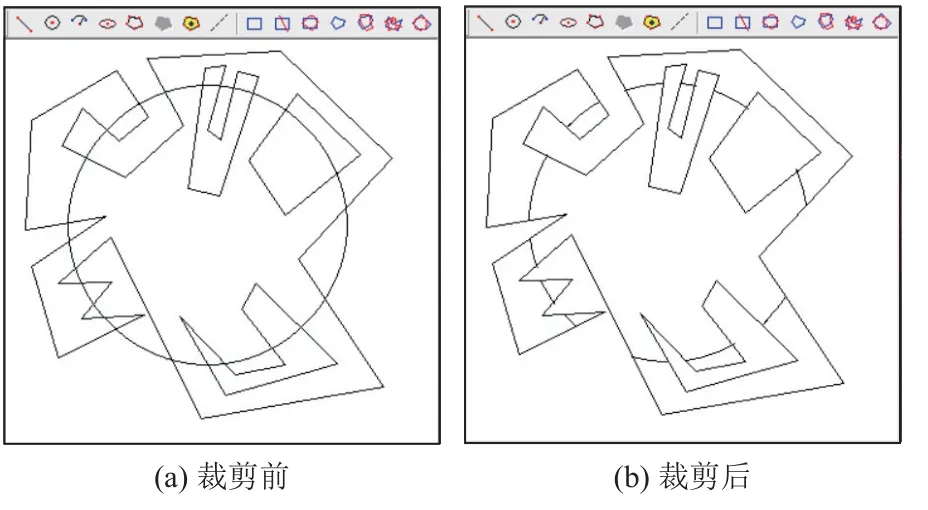
圖9 帶內環的多邊形裁剪窗口的圓裁剪

本實驗中采用的直線、多邊形、圓以及圓弧這些圖形的生成方法均為筆者自己開發的算法實現, 沒有借助Visual C++平臺或者其他如OpenGL圖形庫現有的繪圖函數生成, 為了說明本文算法的效率和性能, 下面列出本文方法和文獻方法在步驟上的區別比較.

表1是本文算法與文獻算法的比較. 其中, 在判斷和計算裁剪邊界直線和圓的交點時, 本文算法的時間復雜度是 O (n) , 其中n為多邊形的邊的數量, 空間復雜度為O (k), 其中k為實交點的數量, 對交點排序時的復雜度為O (k), 空間復雜度為O (1), 也即本文和文獻在共有的算法步驟中的時間復雜度和空間復雜度是相同的.但是, 除了共有的步驟外, 文獻算法還需要其他步驟才能實現, 而本文的算法, 僅根據交點在多邊形邊所在直線的參數值大小, 判斷出交點的進出點特性, 即可進行裁剪, 不需要太多步驟, 因此效率更高. 另外, 文獻也沒有考慮多邊形裁剪窗口帶內環的情況, 本文算法不僅適用于僅有外環的一般多邊形裁剪窗口, 也適用于帶內環的任意多邊形裁剪窗口的圓裁剪, 因此, 算法更具有通用性.

表1 本文算法和文獻算法[23–25]的比較

6 結論

本文提出了一種基于交點參數信息分析的任意多邊形裁剪窗口的圓裁剪算法, 在計算多邊形邊與圓交點的同時, 通過交點在邊所在直線的參數信息, 即可識別出交點的進出點特性, 從而實現對圓的裁剪. 與文獻中的方法相比較, 本算法步驟較少, 編程實例結果也驗證了本文算法的可行性. 本文的算法不僅對僅有外環的一般多邊形裁剪窗口的圓裁剪適用, 也適用于帶內環的任意多邊形裁剪窗口的圓裁剪.