一種采用雙彎管儲(chǔ)氣段布局的高超聲速Ludwieg管設(shè)計(jì)

趙家權(quán)，司馬學(xué)昊，黃冉冉，熊有德，余 濤，吳 杰

(華中科技大學(xué)，武漢 430074)

0 引言

高超聲速空氣動(dòng)力學(xué)是先進(jìn)高超聲速飛行器設(shè)計(jì)的基礎(chǔ)，但目前仍有諸多難題尚未完全解決，如高超聲速邊界層層流-湍流轉(zhuǎn)捩[1-5]、激波-邊界層干擾[6]、真實(shí)氣體效應(yīng)和多物理場(chǎng)耦合[7]等。為了突破高超聲速空氣動(dòng)力學(xué)難題，提升先進(jìn)高超聲速飛行器的精細(xì)化設(shè)計(jì)能力，需要持續(xù)開展高超聲速空氣動(dòng)力學(xué)基礎(chǔ)研究。通常而言，開展高超聲速空氣動(dòng)力學(xué)研究主要有三大手段，分別是風(fēng)洞試驗(yàn)、數(shù)值模擬和飛行試驗(yàn)。近年來，高精度數(shù)值模擬和飛行試驗(yàn)都取得了較大的進(jìn)步，風(fēng)洞試驗(yàn)得益于豐富的地面測(cè)試手段，可以以較低成本反映流場(chǎng)物理機(jī)理，也得到了科研人員的廣泛認(rèn)可。但是，常規(guī)高超聲速風(fēng)洞的建設(shè)和運(yùn)行成本昂貴，測(cè)試儀器的價(jià)格往往也不菲，一定程度上阻礙了高超聲速試驗(yàn)空氣動(dòng)力學(xué)的基礎(chǔ)研究的發(fā)展。為了便于基礎(chǔ)科研機(jī)構(gòu)開展高超聲速空氣動(dòng)力學(xué)試驗(yàn)研究，Ludwieg在1955年首次提出了Ludwieg管的設(shè)計(jì)概念[8]。Ludwieg管結(jié)構(gòu)簡(jiǎn)單，無須復(fù)雜的壓力控制系統(tǒng)，尤其在使用快開主控閥門替代傳統(tǒng)膜片后，其建造與運(yùn)行成本相比常規(guī)下吹式高超聲速風(fēng)洞均大幅下降[9]。目前，高超聲速Ludwieg管風(fēng)洞已經(jīng)得到了廣泛應(yīng)用，如德國(guó)不倫瑞克工業(yè)大學(xué)馬赫數(shù)3和馬赫數(shù)6 Ludwieg管 風(fēng) 洞[9-10]、美國(guó)普渡大學(xué)馬赫數(shù)6 Ludwieg管靜音風(fēng)洞[11]、美國(guó)空軍實(shí)驗(yàn)室馬赫數(shù)6 Ludwieg管風(fēng)洞[12]、圣母大學(xué)馬赫數(shù)6 Ludwieg管靜音風(fēng)洞[13]、我國(guó)中國(guó)空氣動(dòng)力研究與發(fā)展中心的馬赫數(shù)6 Ludwieg管靜音風(fēng)洞等。根據(jù)德國(guó)不倫瑞克工業(yè)大學(xué)Radespiel等[9]的估算，一座口徑為Φ0.5 m的馬赫數(shù)6 Ludwieg管風(fēng)洞整體建造費(fèi)用約為100萬歐元，對(duì)應(yīng)的每車次運(yùn)行成本約為1歐元。另一方面，受限于Ludwieg管風(fēng)洞的運(yùn)行原理，以上提及的高超聲速Ludwieg管風(fēng)洞通常采用直管作為核心部件儲(chǔ)氣段的布局設(shè)計(jì)。以運(yùn)行有效時(shí)間為100 ms的Ludwieg管風(fēng)洞為例，其儲(chǔ)氣段的長(zhǎng)度需要達(dá)到17 m以上，對(duì)實(shí)驗(yàn)室的空間與場(chǎng)地要求較高。又如德國(guó)不倫瑞克工業(yè)大學(xué)、美國(guó)普渡大學(xué)、圣母大學(xué)以及我國(guó)中國(guó)空氣動(dòng)力研究與發(fā)展中心的Ludwieg管風(fēng)洞均采用長(zhǎng)直儲(chǔ)氣段布局，長(zhǎng)度往往達(dá)到20 m以上。對(duì)于儲(chǔ)氣段采用彎管氣動(dòng)布局這種形式，盡管Koppenwallner[14]、Schrijer等[15]及美國(guó)空軍實(shí)驗(yàn)室[12]都進(jìn)行了嘗試，但是彎管的參數(shù)選擇更多來自經(jīng)驗(yàn)，并未對(duì)其具體氣動(dòng)影響開展研究。針對(duì)Ludwieg管儲(chǔ)氣段采用彎管布局產(chǎn)生的氣動(dòng)影響不確定的問題，作者團(tuán)隊(duì)進(jìn)行了基于雙彎管儲(chǔ)氣段布局的高超聲速Ludwieg管氣動(dòng)設(shè)計(jì)，并重點(diǎn)探究了雙彎管儲(chǔ)氣段設(shè)計(jì)的氣動(dòng)影響。文章首先介紹高超聲速Ludwieg管的運(yùn)行原理；之后對(duì)Laval噴管型線與風(fēng)洞的非定常啟動(dòng)過程進(jìn)數(shù)值分析；而后基于建造的Φ0.25 m馬赫數(shù)6 Ludwieg管風(fēng)洞，對(duì)運(yùn)行狀態(tài)進(jìn)行初步測(cè)量，并將試驗(yàn)結(jié)果與數(shù)值預(yù)測(cè)進(jìn)行對(duì)比分析。

1 Ludwieg管理論設(shè)計(jì)

高超聲速Ludwieg管風(fēng)洞的運(yùn)行原理如圖1所示。風(fēng)洞的高壓儲(chǔ)氣段與Laval噴管通過快速控制閥門分開。在風(fēng)洞啟動(dòng)前，儲(chǔ)氣段內(nèi)儲(chǔ)存著高溫高壓空氣，控制閥門下游的部分則通過真空泵抽成了真空。在開啟快速控制閥門的瞬間，會(huì)產(chǎn)生一系列的非定常膨脹波，該膨脹波以聲速向儲(chǔ)氣段的上游行進(jìn)（圖1的CD段分別表示該膨脹波的波頭和波尾）；該膨脹波驅(qū)動(dòng)管內(nèi)的氣體達(dá)到儲(chǔ)氣段啟動(dòng)馬赫數(shù)。當(dāng)膨脹波以當(dāng)?shù)芈曀俚竭_(dá)儲(chǔ)氣段尾端后，再次被反射回來（AE和BF）。當(dāng)反射膨脹波到達(dá)快速控制閥時(shí)，快速控制閥門關(guān)閉，風(fēng)洞的運(yùn)行結(jié)束。與此同時(shí)，在快速控制閥的下游，受壓差驅(qū)動(dòng)，氣流在Laval噴管喉部形成聲速流，并沿著Laval噴管膨脹加速，在試驗(yàn)段時(shí)獲得對(duì)應(yīng)設(shè)計(jì)馬赫數(shù)的高超聲速氣流。

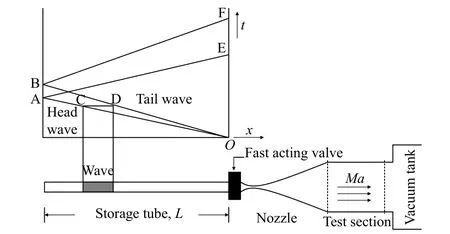
圖1 Ludwieg管風(fēng)洞的運(yùn)行原理圖[16]Fig. 1 Principle diagram of the Ludwieg tube tunnel[16]

儲(chǔ)氣段膨脹波前后的總溫和總壓關(guān)系可通過以下關(guān)系式獲得[17]：

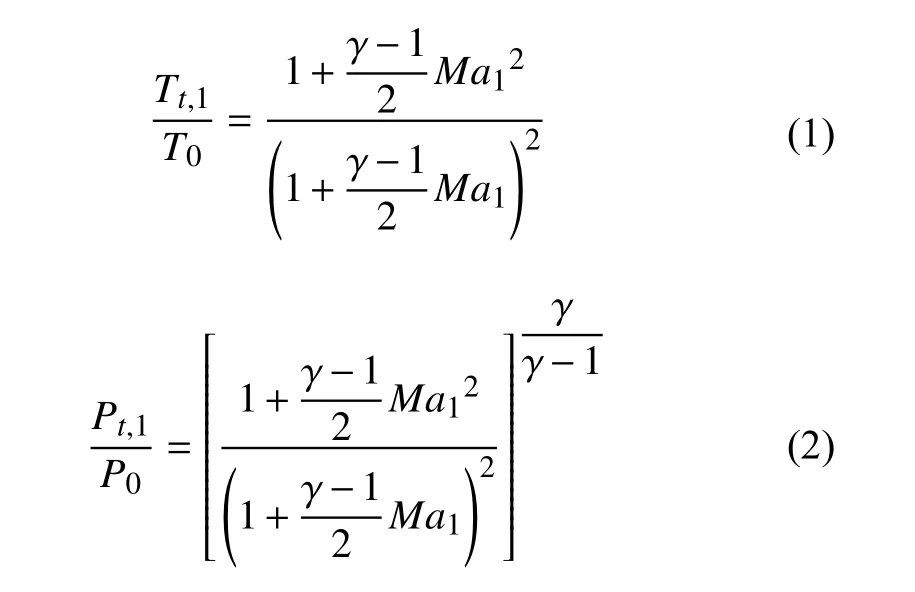
其中：下角標(biāo)0代表風(fēng)洞未啟動(dòng)的初始狀態(tài)，（t,1）代表快速控制閥（快開閥）開啟后儲(chǔ)氣段內(nèi)膨脹波傳播后的總狀態(tài)；Ma1為L(zhǎng)udwieg管風(fēng)洞儲(chǔ)氣段的啟動(dòng)馬赫數(shù)；γ為理想氣體的比熱容比。膨脹波系在儲(chǔ)氣段往返運(yùn)行一次對(duì)應(yīng)管風(fēng)洞一個(gè)周期，可由式（3）估算：

式中，L為儲(chǔ)氣段的總長(zhǎng)度，a為當(dāng)?shù)芈曀佟Ｓ墒剑?）可知，通過延長(zhǎng)儲(chǔ)氣段的總長(zhǎng)度可以有效增加Ludwieg管風(fēng)洞的運(yùn)行時(shí)間。為了確保Ludwieg管風(fēng)洞100 ms的運(yùn)行時(shí)間，儲(chǔ)氣段的長(zhǎng)度需要達(dá)到17 m以上。受試驗(yàn)場(chǎng)地限制，本管風(fēng)洞的儲(chǔ)氣段采用了雙彎管的設(shè)計(jì)，具體構(gòu)成包括3段6.5 m長(zhǎng)的直管與2個(gè)U型接頭，其中U型接頭中心直徑為0.4 m，儲(chǔ)氣段的內(nèi)徑為0.1 m。采用雙彎管設(shè)計(jì)后，儲(chǔ)氣段的總長(zhǎng)度為22 m。

2 數(shù)值方法

數(shù)值模擬采用SU2開源求解器[18]。該求解器采用二階有限體積法，可進(jìn)行從低速不可壓流動(dòng)到高超聲速的計(jì)算，滿足設(shè)計(jì)的定常與非定常模擬需求。為了準(zhǔn)確模擬高超聲速流動(dòng)，所采用的湍流模式為標(biāo)準(zhǔn)Menter SST兩方程湍流模型，空間離散采用AUSM格式。

2.1 網(wǎng)格結(jié)構(gòu)與邊界條件設(shè)置

為了獲得更為準(zhǔn)確的結(jié)果，Laval噴管建模采用1/4模型，如圖2所示。該模型采用全結(jié)構(gòu)化網(wǎng)格生成，壁面第一層網(wǎng)格高度y+為5。1/4模型的左右兩側(cè)為對(duì)稱邊界條件，入口和出口分別參考該Ludwieg管風(fēng)洞實(shí)際運(yùn)行工況，其中入口定義為壓力入口邊界，出口為壓力出口邊界。

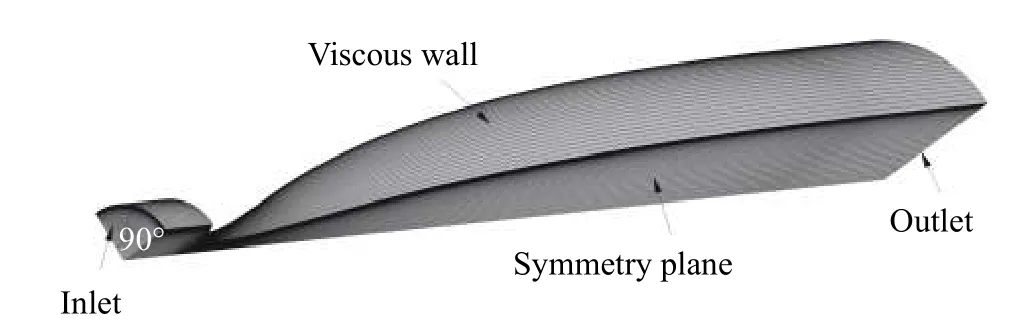
圖2 Laval噴管網(wǎng)格拓?fù)浣Y(jié)構(gòu)Fig. 2 Mesh topology of the Laval nozzle

由于該Laval噴管為中心軸對(duì)稱體，網(wǎng)格獨(dú)立性分析選擇了以二維中心軸對(duì)稱邊界的情況，噴管周向的網(wǎng)格分布將參考Wu等之前已經(jīng)開展過的研究[19]。在二維網(wǎng)格獨(dú)立性分析中，分別比較了372×45、442×55、497×65、502×75四種不同網(wǎng)格密度下Laval噴管出口處的馬赫數(shù)分布。由圖3可知，網(wǎng)格密度為497×65時(shí)Laval噴管出口處的馬赫數(shù)分布與密度為502×75的分布幾乎一致，因此選442×55作為L(zhǎng)aval噴管型線優(yōu)化的參考網(wǎng)格密度。

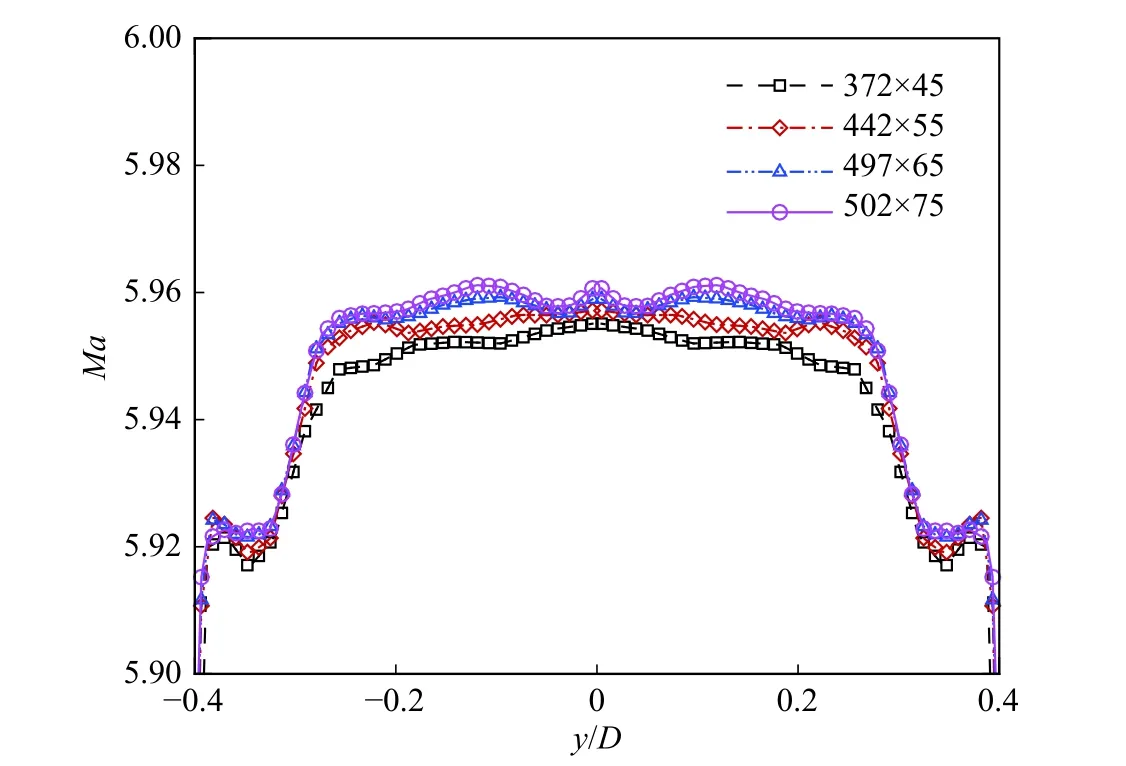
圖3 網(wǎng)格無關(guān)性分析Fig. 3 Mesh independent test

此外，為了開展風(fēng)洞的啟動(dòng)過程以及儲(chǔ)氣段雙彎管設(shè)計(jì)影響分析，需要進(jìn)行全風(fēng)洞的非定常數(shù)值模擬。但是采用雙彎管儲(chǔ)氣段布局的模型非中心軸對(duì)稱體，故采用了風(fēng)洞的半模進(jìn)行建模，其網(wǎng)格拓?fù)淙鐖D4所示。模型同樣采用全結(jié)構(gòu)化網(wǎng)格生成，總網(wǎng)格量為550萬。

2.2 求解器驗(yàn)證

盡管SU2開源求解器具有求解高超聲速流場(chǎng)的能力[18]，但是相關(guān)工作仍然比較少見。為了驗(yàn)證數(shù)值模擬的可靠性，基于德國(guó)不倫瑞克工業(yè)大學(xué)Ludwieg管風(fēng)洞馬赫數(shù)6的Laval噴管的型線進(jìn)行了求解器的驗(yàn)證。在采用同樣的數(shù)值方法、邊界條件和計(jì)算網(wǎng)格的前提下，將SU2計(jì)算的結(jié)果與其他求解器進(jìn)行了比較。圖5顯示了分別使用DLR-TAU Code、直接數(shù)值模擬[20]和SU2計(jì)算的馬赫數(shù)6的 Laval噴管中心軸上的馬赫數(shù)分布，三者吻合良好，表明SU2求解器可用于本文高超聲速管道流動(dòng)的模擬。

3 數(shù)值結(jié)果與分析

3.1 Laval噴管優(yōu)化設(shè)計(jì)

Laval噴管是Ludwieg管風(fēng)洞的主要部件，決定了風(fēng)洞試驗(yàn)段的流場(chǎng)均勻性。典型的Laval噴管通常由收縮段、喉道以及擴(kuò)張段組成。為了確保快開閥與收縮段的型面嚙合，此次Laval噴管的收縮段設(shè)計(jì)采用三次樣條曲線。在收縮比確定的情況下，開展了不同收縮段長(zhǎng)度對(duì)噴管出口處流場(chǎng)影響的研究。噴管喉道采用圓弧設(shè)計(jì)，確保亞聲速流動(dòng)到超聲速的均勻過渡。噴管的擴(kuò)張段則采用了經(jīng)典的Sivells方法[21]。由于此次Ludwieg管的設(shè)計(jì)定位是常規(guī)噪聲型高超聲速風(fēng)洞，噴管的型線設(shè)計(jì)需要重點(diǎn)滿足出口處核心區(qū)域馬赫數(shù)分布的均勻性，而Laval噴管的長(zhǎng)度極大程度上決定了風(fēng)洞的建設(shè)成本，因此Laval噴管的設(shè)計(jì)重點(diǎn)放在了收縮段與擴(kuò)張段的長(zhǎng)度優(yōu)化上，在流場(chǎng)品質(zhì)達(dá)標(biāo)的前提下盡量確保縮短Laval噴管的長(zhǎng)度。

在收縮段的設(shè)計(jì)優(yōu)化中，其長(zhǎng)度變化范圍為34.4～102.4 mm。為了便于比較，將收縮段長(zhǎng)度為34.4 mm的情況定義為參考長(zhǎng)度（contraction length of benchmark，CLB），不同收縮段長(zhǎng)度下流場(chǎng)馬赫數(shù)分布比較見圖6。

圖6 不同收縮段長(zhǎng)度下Laval噴管馬赫數(shù)云圖比較Fig. 6 Mach number contour comparison for Laval nozzels with different contraction lengths

由馬赫數(shù)云圖可知，在參考收縮段長(zhǎng)度下，雖然Laval噴管存在馬赫數(shù)分布梯度，但是出口區(qū)域已經(jīng)獲得了較為均勻的高超聲速流動(dòng)。當(dāng)收縮段長(zhǎng)度增加到1.5倍參考長(zhǎng)度時(shí)，Laval噴管的出口區(qū)域的均勻度進(jìn)一步提升，之前存在的馬赫數(shù)分布梯度消失。當(dāng)收縮段長(zhǎng)度為1.8倍以及2.5倍參考長(zhǎng)度時(shí)，噴管出口處的馬赫數(shù)分布保持在均勻分布狀態(tài)。但是當(dāng)收縮段長(zhǎng)度為3倍參考長(zhǎng)度時(shí)，噴管出口處的馬赫數(shù)云圖反而呈現(xiàn)不均勻分布。

進(jìn)一步，比較了Laval噴管中心軸以及出口處的馬赫數(shù)分布，如圖7和圖8所示。整體而言，不同收縮段長(zhǎng)度下馬赫數(shù)的分布均相似。但是，將局部馬赫數(shù)的分布放大后可以區(qū)別不同收縮段長(zhǎng)度下流場(chǎng)的差異。圖7中的局部放大圖是顯示Laval噴管中馬赫數(shù)在x/D= 3.0處獲得馬赫數(shù)峰值后下降（注：D表示Laval噴管的出口直徑），在噴管核心區(qū)域x/D= 3.5～5.9區(qū)間呈現(xiàn)振蕩分布。當(dāng)收縮段長(zhǎng)度為34.4 mm時(shí)，x/D= 3.5～5.9區(qū)間流向馬赫數(shù)的最大相對(duì)偏差為0.16%；當(dāng)收縮段長(zhǎng)度增加到1.5倍參考長(zhǎng)度時(shí)，馬赫數(shù)的最大相對(duì)偏差下降到了0.107%；隨著收縮段長(zhǎng)度的進(jìn)一步增加，噴管核心流動(dòng)區(qū)域的馬赫數(shù)最大相對(duì)偏差反而增加到0.13%。噴管出口處的縱向馬赫數(shù)分布如圖8所示。通過圖8中的局部放大圖可知，噴管收縮段的長(zhǎng)度影響了噴管出口處的馬赫數(shù)幅值。當(dāng)收縮段長(zhǎng)度為34.4 mm時(shí)，噴管出口處核心流區(qū)域馬赫數(shù)最大相對(duì)偏差為0.034%（注明：分析區(qū)域y/D為?0.23～0.23）；當(dāng)收縮段長(zhǎng)度增加到1.5倍參考長(zhǎng)度時(shí)，馬赫數(shù)的最大相對(duì)偏差下降到了0.061%；隨著收縮段長(zhǎng)度的進(jìn)一步增加，噴管出口處核心流動(dòng)區(qū)域馬赫數(shù)分布最大相對(duì)偏差保持在0.054%。綜合比較不同收縮段長(zhǎng)度下Laval噴管核心區(qū)域流向和縱向馬赫數(shù)分布的最大相對(duì)偏差，確定此次Laval噴管收縮段的長(zhǎng)度為1.5倍參考長(zhǎng)度。

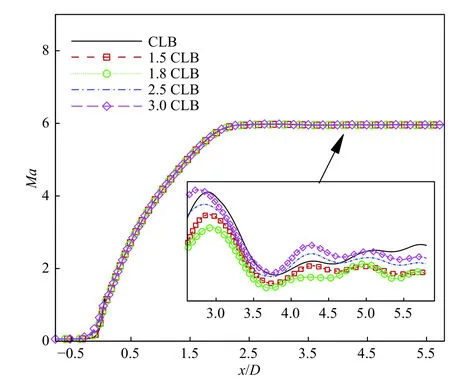
圖7 不同收縮段長(zhǎng)度下Laval噴管中心軸馬赫數(shù)分布比較Fig. 7 Comparison of Mach number distributions along the centerline of the Laval nozzle with different contraction lengths

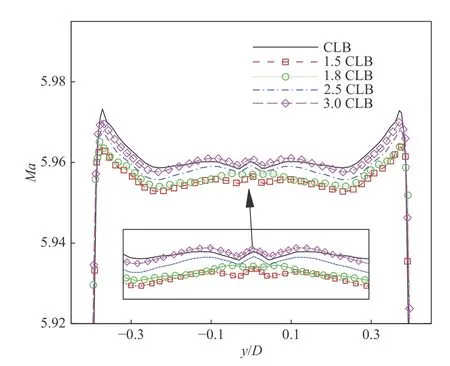
圖8 不同收縮段長(zhǎng)度下Laval噴管出口處馬赫數(shù)分布比較Fig. 8 Comparison of Mach number distributions at the exit of the Laval nozzle with different contraction lengths

擴(kuò)張段作為L(zhǎng)aval噴管的關(guān)鍵設(shè)計(jì)部分，直接影響了高超聲速氣流的品質(zhì)。通常噴管長(zhǎng)度越長(zhǎng)，高超聲速流動(dòng)的膨脹越緩慢，噴管出口處的高超聲速流動(dòng)的均勻性也越好。但是，噴管長(zhǎng)度越長(zhǎng)，其加工成本越高，型面精度控制難度也越大，風(fēng)洞試驗(yàn)段的有效口徑也更小。因此，Laval噴管擴(kuò)張段的優(yōu)化需要在噴管的長(zhǎng)度與流場(chǎng)品質(zhì)上進(jìn)行折中。選擇了對(duì)5組不同擴(kuò)張段長(zhǎng)度進(jìn)行全Laval噴管數(shù)值模擬，馬赫數(shù)云圖比較見圖9。當(dāng)擴(kuò)張段長(zhǎng)度為L(zhǎng)/D= 6.1時(shí)，噴管出口處形成了均勻的高超聲速流場(chǎng)。當(dāng)擴(kuò)張段長(zhǎng)度變?yōu)長(zhǎng)/D= 4.8時(shí)，擴(kuò)張段的流動(dòng)加速更快，但是噴管出口處流場(chǎng)仍呈現(xiàn)均勻分布。隨著擴(kuò)張段長(zhǎng)度進(jìn)一步縮短，擴(kuò)張段的流動(dòng)加速更加劇烈，在噴管出口處可見明顯的馬赫數(shù)梯度分布。

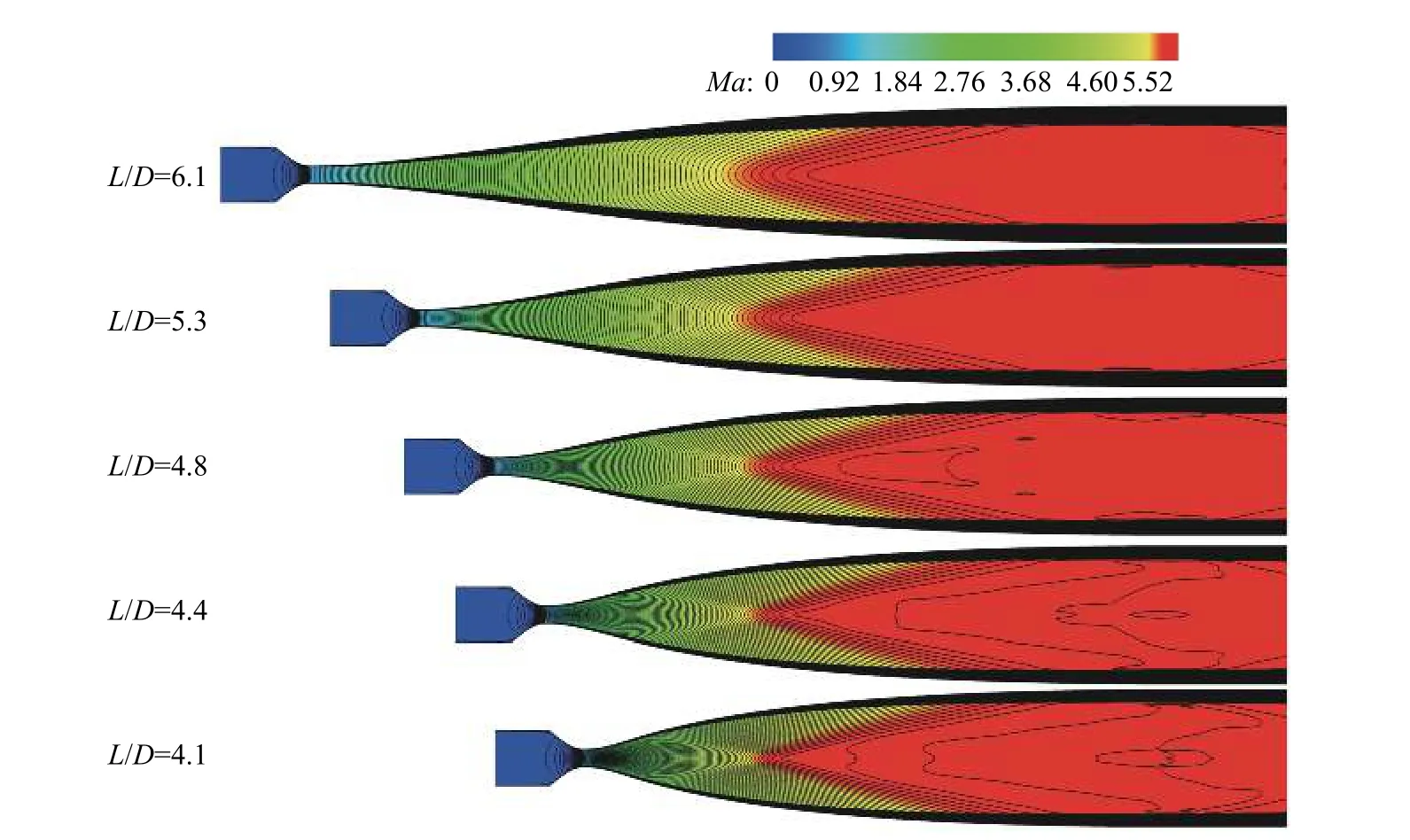
圖9 不同擴(kuò)張段長(zhǎng)度下Laval噴管馬赫數(shù)云圖比較Fig. 9 Comparison of Mach number contours for the Laval nozzels with different expansion lengths

采用同樣的分析方法，將不同擴(kuò)張段長(zhǎng)度下Laval噴管的中心軸和出口處馬赫數(shù)分布進(jìn)行提取與比較，分析噴管核心流動(dòng)區(qū)域馬赫數(shù)的最大相對(duì)偏差，如圖10和圖11所示。由圖10可知，噴管擴(kuò)張段長(zhǎng)度對(duì)流場(chǎng)馬赫數(shù)的分布有明顯影響—噴管越長(zhǎng)，高超聲速氣流加速越平緩，噴管核心流動(dòng)區(qū)域的馬赫數(shù)分布也更為平坦。通過定量分析發(fā)現(xiàn)，當(dāng)噴管擴(kuò)張段長(zhǎng)度由L/D= 6.1變?yōu)長(zhǎng)/D= 4.8時(shí)，噴管核心流動(dòng)區(qū)域流向馬赫數(shù)的最大相對(duì)偏差由0.15%上升到0.3%。當(dāng)擴(kuò)張段的長(zhǎng)度進(jìn)一步縮短后，噴管核心流動(dòng)區(qū)域流向馬赫數(shù)的最大相對(duì)偏差迅速上升到0.64%。

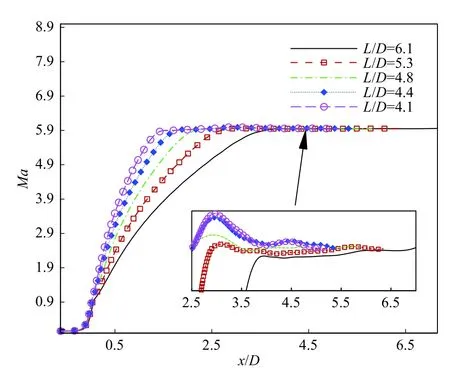
圖10 不同擴(kuò)張段長(zhǎng)度下Laval噴管中心軸馬赫數(shù)分布比較Fig. 10 Comparison of Mach number distributions along the centerline of the Laval nozzle with different expansion lengths

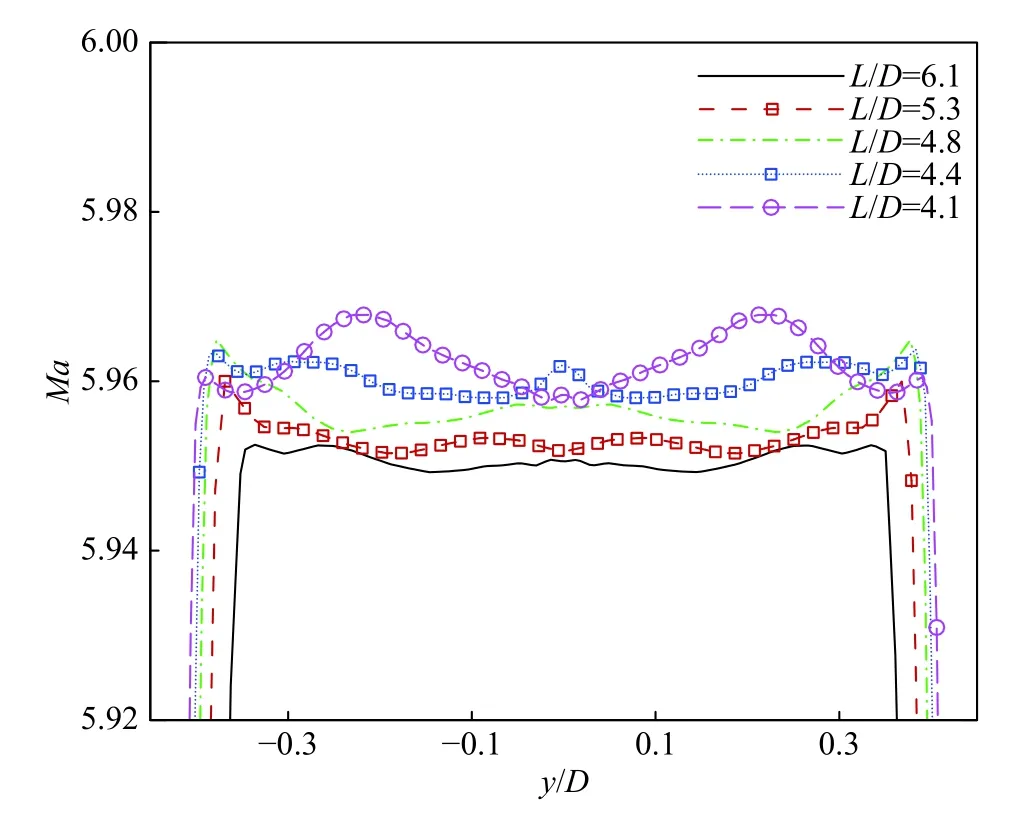
圖11 不同擴(kuò)張段長(zhǎng)度下Laval噴管出口處馬赫數(shù)分布比較Fig. 11 Comparison of Mach number distributions at the exit of the Laval nozzle with different expansion lengths

不同擴(kuò)張段長(zhǎng)度下噴管出口處馬赫數(shù)分布比較見圖11。由該圖可知，當(dāng)噴管擴(kuò)張段長(zhǎng)度為L(zhǎng)/D=6.1時(shí)，馬赫數(shù)的分布最為平坦；與此同時(shí)，由于噴管的長(zhǎng)度最長(zhǎng)，噴管出口處的有效直徑也最小。隨著噴管擴(kuò)張段長(zhǎng)度縮短，噴管出口處馬赫數(shù)最大相對(duì)偏差逐漸增加。在噴管擴(kuò)張段長(zhǎng)度為L(zhǎng)/D= 4.1時(shí)，噴管出口處馬赫數(shù)最大相對(duì)偏差為0.166%，達(dá)到國(guó)軍標(biāo)GJB 4399—2002馬赫數(shù)最大相對(duì)偏差要求。綜合考慮流場(chǎng)品質(zhì)以及建造成本，該Laval噴管的擴(kuò)張段長(zhǎng)度選擇了L/D= 4.8。

3.2 快開閥對(duì)流場(chǎng)影響分析

快開閥主控閥門作為本風(fēng)洞的設(shè)計(jì)特點(diǎn)之一，大幅提升了Ludwieg管風(fēng)洞的運(yùn)行效率。但是，快開閥位于Laval噴管喉道前，其存在對(duì)試驗(yàn)段流場(chǎng)的影響需要明晰。在此分別針對(duì)Laval噴管有無快開閥的情況進(jìn)行了流場(chǎng)模擬，對(duì)應(yīng)的馬赫數(shù)云圖如圖12所示。

由圖12可見，快開閥首先影響了流動(dòng)在擴(kuò)張段的加速收縮，而后受影響的流動(dòng)經(jīng)過擴(kuò)張段膨脹，導(dǎo)致噴管核心區(qū)域流向的馬赫數(shù)分布均勻性有一定程度的降低，但是核心區(qū)域馬赫數(shù)整體仍呈現(xiàn)均勻分布特征。將圖12中不同情況下，噴管出口處的馬赫數(shù)進(jìn)行提取與比較（圖13），可見馬赫數(shù)的分布幾乎一致，但是采用快開閥的情況Laval噴管的邊界層厚度增加了約50%，該現(xiàn)象與Kozulovic等之前發(fā)現(xiàn)的現(xiàn)象相同[22]。

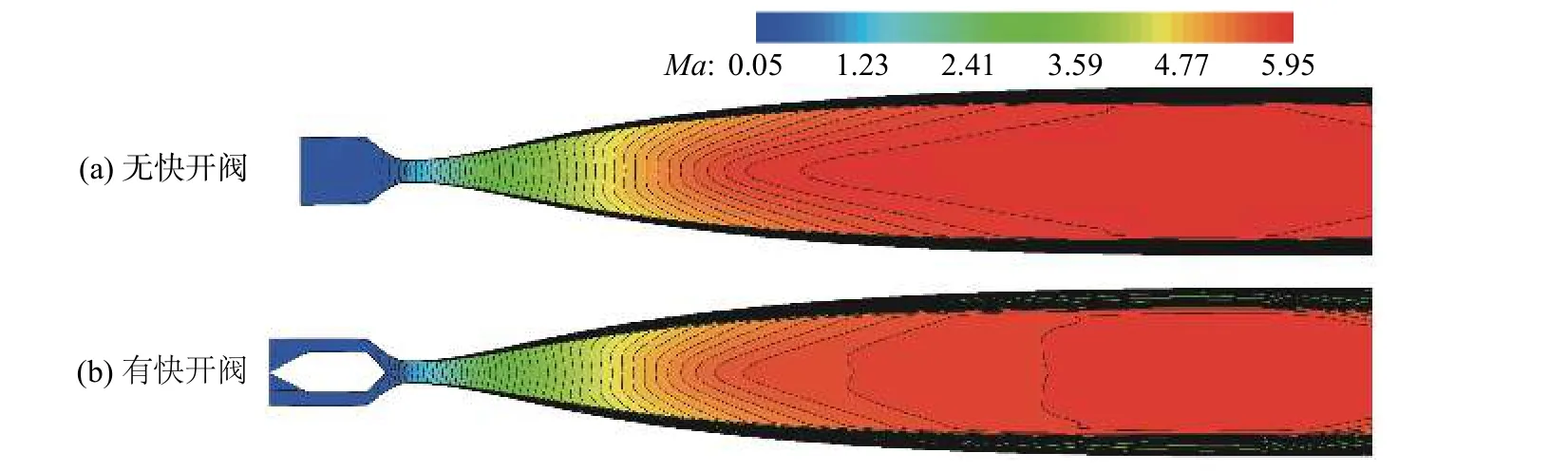
圖12 Laval噴管有無快開閥情況下的馬赫數(shù)云圖對(duì)比Fig. 12 Mach number contour comparison for the Laval nozzel with or without the fast-acting valve

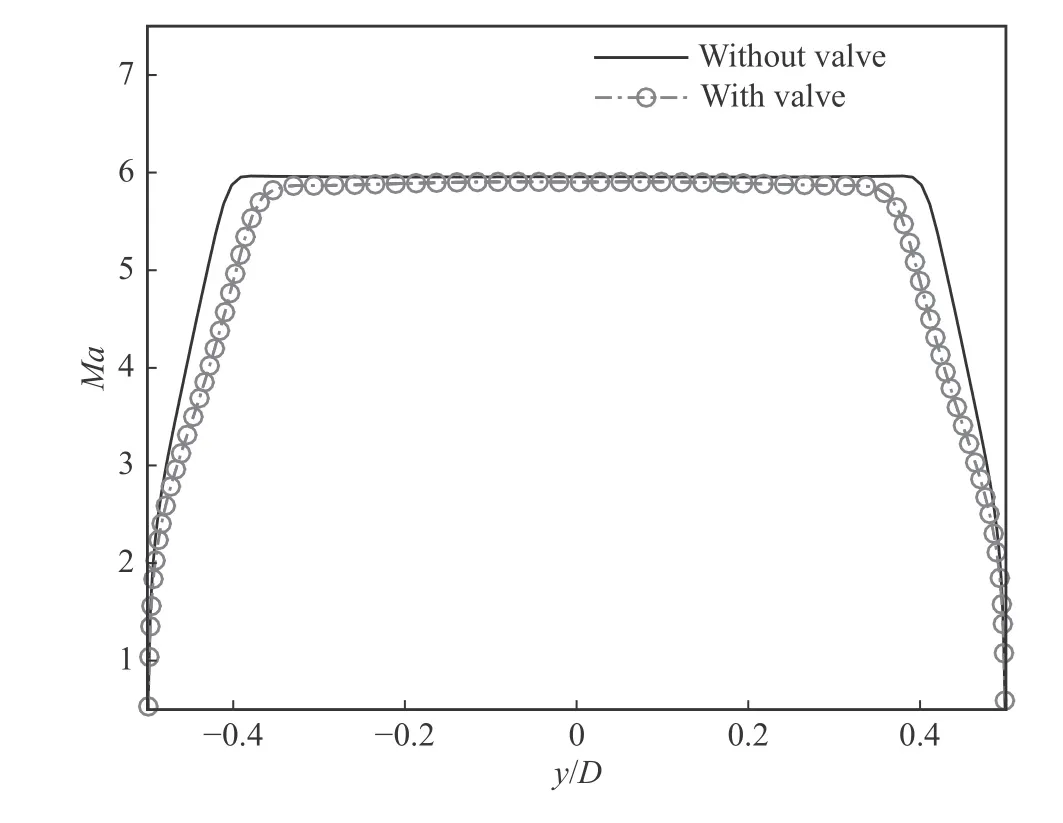
圖13 噴管有無快開閥條件下出口處馬赫數(shù)縱向分布比較Fig. 13 Comparison of Mach number distributions at the exit of the nozzel with or without the fast-acting valve

3.3 Ludwieg管風(fēng)洞啟動(dòng)與運(yùn)行過程分析

圖14顯示了Ludwieg管風(fēng)洞的啟動(dòng)過程，分別給出了風(fēng)洞啟動(dòng)過程中不同時(shí)間點(diǎn)的馬赫數(shù)云圖。由圖可知，風(fēng)洞在2 ms內(nèi)完成了啟動(dòng)過程，在噴管出口處形成了馬赫數(shù)6高超聲速流動(dòng)。之后，高超聲速流動(dòng)將持續(xù)直至反射的膨脹波達(dá)到噴管的收縮段。

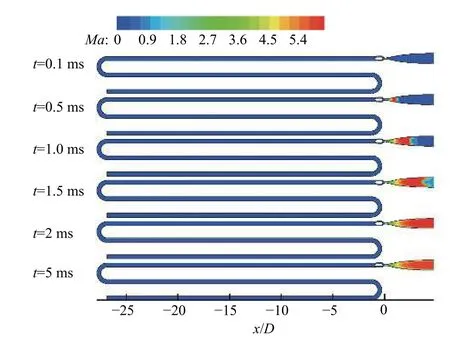
圖14 Ludwieg管風(fēng)洞啟動(dòng)過程馬赫數(shù)云圖變化（P0 = 10 bar，T0 = 300 K）Fig. 14 Mach number contour variation during the starting process of the Ludwieg tube tunnel (P0 = 10 bar, T0 = 300 K)

圖15 展示了風(fēng)洞運(yùn)行過程中不同時(shí)間節(jié)點(diǎn)膨脹波系在儲(chǔ)氣段的演化特征。t= 2.23 ms時(shí)，Laval噴管的出口處已經(jīng)形成了高超聲速流動(dòng)，膨脹波系處于快開閥上游，波系整體強(qiáng)度較高；隨著風(fēng)洞的穩(wěn)定運(yùn)行，膨脹波系朝向儲(chǔ)氣段尾部行進(jìn)，在t= 22.23 ms時(shí)到達(dá)儲(chǔ)氣段的第一個(gè)U形接頭，此時(shí)膨脹波系的強(qiáng)度減弱；在t= 68.23 ms時(shí)，膨脹波系到達(dá)儲(chǔ)氣段的尾部，發(fā)生反射，轉(zhuǎn)而朝向快開閥行進(jìn)；在t= 121.23 ms時(shí)，膨脹波系到達(dá)了Laval噴管的收縮段，膨脹波的強(qiáng)度大幅減弱；在t= 127.23 ms時(shí)，通過膨脹波波頭強(qiáng)度可以得知膨脹波已經(jīng)發(fā)生反射，風(fēng)洞運(yùn)行處于第二個(gè)運(yùn)行周期。在Ludwieg管風(fēng)洞單個(gè)運(yùn)行周期中，Laval噴管段的流動(dòng)處于穩(wěn)定狀態(tài)，而膨脹波波系處于持續(xù)減弱狀態(tài)。

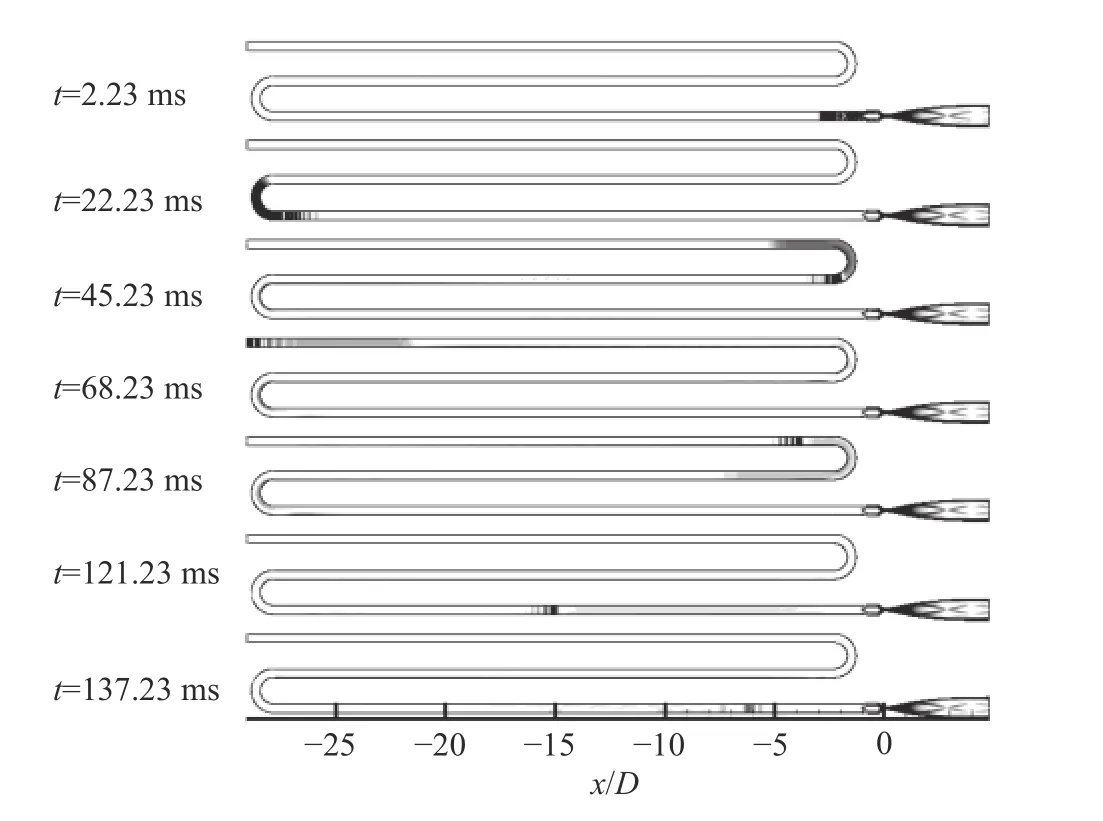
圖15 Ludwieg管風(fēng)洞運(yùn)行過程密度梯度云圖變化（P0 = 10 bar，T0 = 300 K）Fig. 15 Density gradient contour variation during the operation process of the Ludwieg tube tunnel(P0 = 10 bar, T0 = 300 K)

更進(jìn)一步，分析了Ludwieg管風(fēng)洞運(yùn)行過程中快開閥上游位置x= –1.5D處縱向馬赫數(shù)和壓力隨時(shí)間的分布變化特征，如圖16和圖17所示。由圖16可見，在t= 2 ms時(shí)，膨脹波還未達(dá)到x= –1.5D處，該處流動(dòng)尚未啟動(dòng)，盡管Laval噴管已經(jīng)形成了高超聲速氣流；在t= 2.23 ms時(shí)，膨脹波到達(dá)該位置，并形成了啟動(dòng)馬赫數(shù)0.058。隨著風(fēng)洞的穩(wěn)定運(yùn)行，膨脹波系沿著儲(chǔ)氣段發(fā)展，在x= –1.5D處的邊界層厚度也由t= 2.23 ms時(shí)儲(chǔ)氣段直徑的7%增長(zhǎng)到了t= 121.23 ms時(shí)儲(chǔ)氣段直徑的67%。值得注意的是，在該過程中由于邊界層的厚度持續(xù)增長(zhǎng)，x= –1.5D處的馬赫數(shù)始終處于增長(zhǎng)趨勢(shì)。在t= 123.23 ms時(shí)，x= –1.5D處的馬赫數(shù)開始下降，表明Ludwieg管風(fēng)洞的一個(gè)穩(wěn)定運(yùn)行周期已結(jié)束。

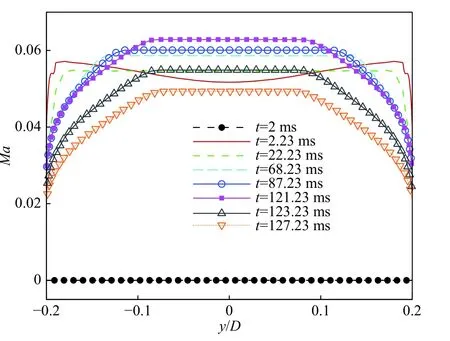
圖16 x = –1.5D位置不同時(shí)刻馬赫數(shù)分布比較Fig. 16 Comparison of Mach number distributions at x = –1.5D for different time instances

圖17顯示了x= –1.5D處不同時(shí)刻總壓分布的變化特征。由該圖可知，隨著膨脹波系的運(yùn)動(dòng)，總壓由10 bar變?yōu)榱?.25 bar，滿足式（2）；此外，在Ludwieg管風(fēng)洞的一個(gè)運(yùn)行周期內(nèi)，即從t= 2.23～121.23 ms內(nèi)，該處的總壓幾乎保持不變。當(dāng)一個(gè)運(yùn)行周期結(jié)束后，膨脹波系重復(fù)之前的運(yùn)動(dòng)，形成臺(tái)階狀的總壓分布特征。

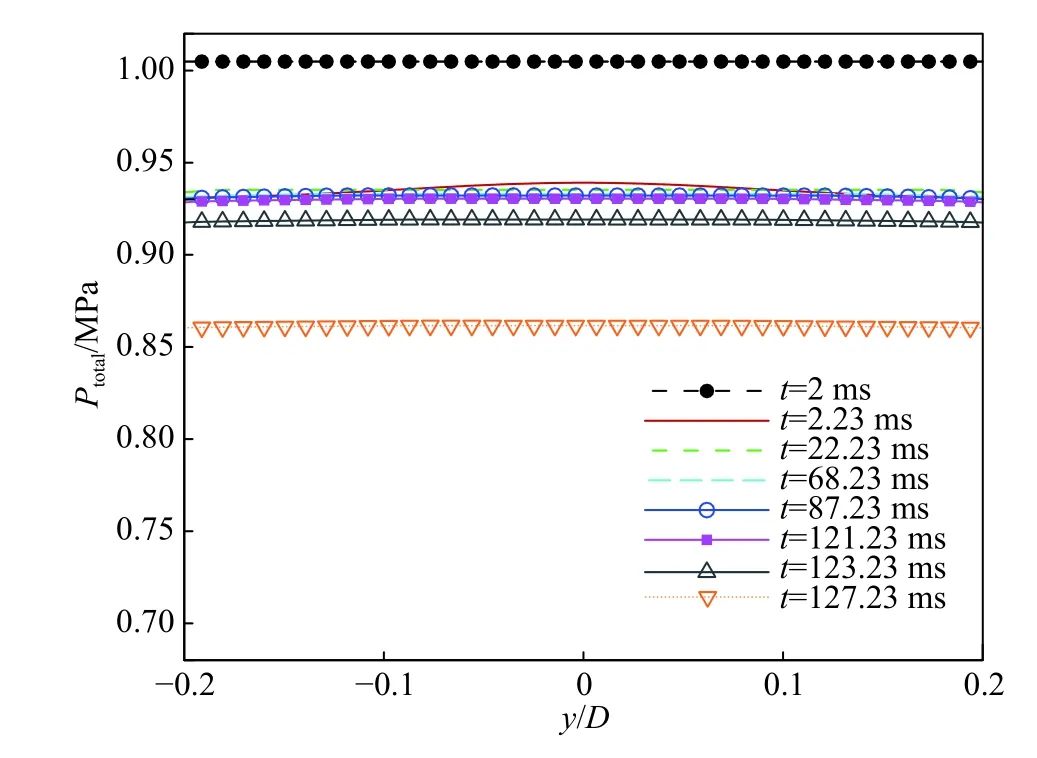
圖17 x = –1.5D位置不同時(shí)刻總壓分布比較Fig. 17 Comparison of total pressure distributions at x = –1.5D for different time instances

3.4 彎管對(duì)Ludwieg管流場(chǎng)的影響分析

為了認(rèn)識(shí)儲(chǔ)氣段采用彎管布局對(duì)Ludwieg管流場(chǎng)的影響，首先對(duì)膨脹波系經(jīng)過第一個(gè)U形接頭的過程進(jìn)行了分析，如圖18所示。在t= 22.23 ms時(shí)，膨脹波波頭快到達(dá)U形接頭，此時(shí)膨脹波為平面波。當(dāng)膨脹波遇到U形接頭后，膨脹波系的運(yùn)動(dòng)受離心力作用呈現(xiàn)非對(duì)稱分布，在U形接頭外側(cè)膨脹波強(qiáng)度較高，而內(nèi)側(cè)強(qiáng)度較弱；即使如此，此處并未觀察到明顯膨脹波反射現(xiàn)象。當(dāng)膨脹波系進(jìn)一步行進(jìn)，其逐漸恢復(fù)為平面波。

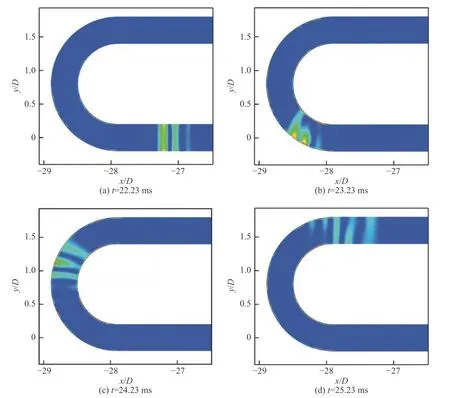
圖18 膨脹波系經(jīng)過第一個(gè)U形接頭的密度梯度的云圖Fig. 18 Density gradient contours of the expansion waves passing through the first U-tube joint

圖19展示了采用雙彎管的儲(chǔ)氣段中心軸上膨脹波波圖，其中Δx-t的斜率表示膨脹波行進(jìn)的速度。由所繪出的波圖可知，風(fēng)洞在運(yùn)行過程中膨脹波在彎管部分的斜率并未發(fā)生明顯變化，更進(jìn)一步表明采用本彎管設(shè)計(jì)參數(shù)時(shí)膨脹波的行進(jìn)并未受到明顯影響。此外，該圖還展現(xiàn)了Ludwieg管風(fēng)洞一個(gè)運(yùn)行周期內(nèi)儲(chǔ)氣段里高低壓氣流間斷面位置變化信息，并可以確定風(fēng)洞一個(gè)有效周期約為122 ms。

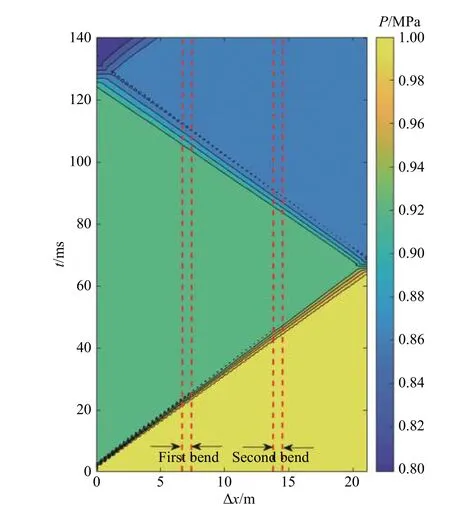
圖19 儲(chǔ)氣段內(nèi)膨脹波系的Δx-t波圖Fig. 19 Δx-t diagram of the expansion waves in the storage tube

最后，提取儲(chǔ)氣段x= –1.2D處的壁面壓力，其隨時(shí)間的變化如圖20所示，可見風(fēng)洞的有效運(yùn)行時(shí)間為121.23 ms。進(jìn)一步將風(fēng)洞的有效運(yùn)行時(shí)間進(jìn)行局部放大，發(fā)現(xiàn)膨脹波在經(jīng)過第二個(gè)彎管處（t= 43 ms和83 ms）儲(chǔ)氣段壓力存在波動(dòng)，相對(duì)偏差僅為0.04%，可以忽略不計(jì)；但是，膨脹波在經(jīng)過第一個(gè)彎管處時(shí)儲(chǔ)氣段壓力不存在類似波動(dòng)。目前該現(xiàn)象的原因尚不清楚，需要進(jìn)一步開展高精度數(shù)值模擬。此外，在單個(gè)風(fēng)洞運(yùn)行周期內(nèi)，儲(chǔ)氣段的壓力下降僅為0.64%。

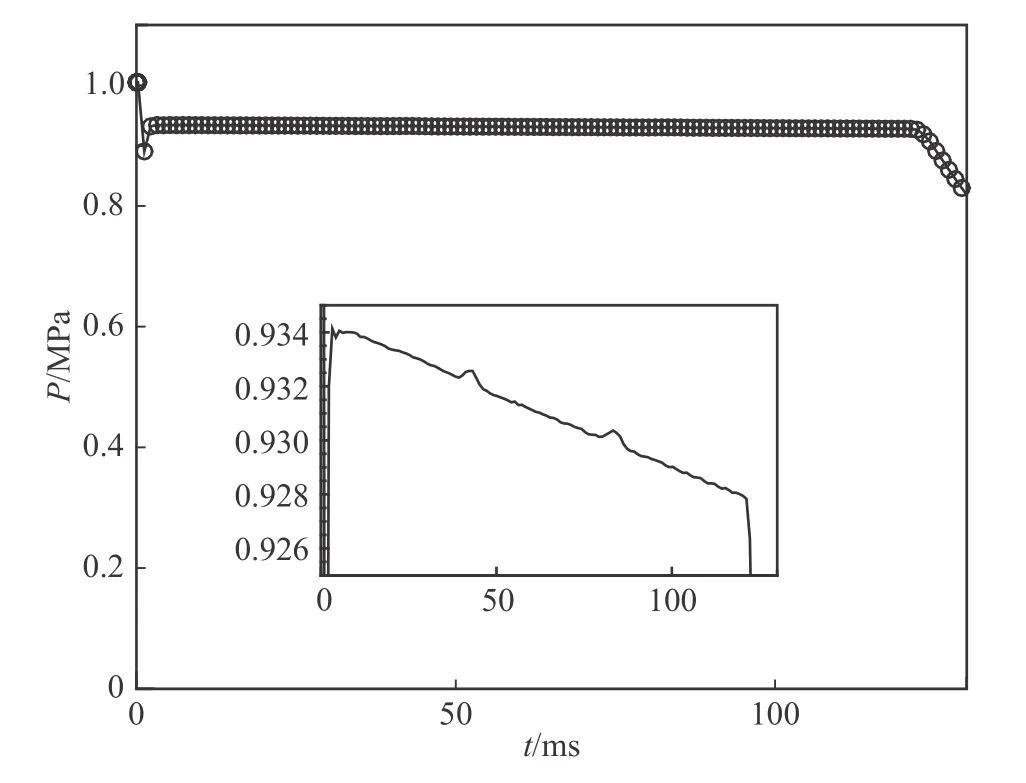
圖20 風(fēng)洞運(yùn)行過程中儲(chǔ)氣段流向位置x = ?1.2D壁面壓力隨時(shí)間變化Fig. 20 Time variation of the wall pressure at x = ?1.2D of the storage tube during the tunnel operation

4 試驗(yàn)驗(yàn)證

基于前文的氣動(dòng)設(shè)計(jì)，在華中科技大學(xué)建成了一座Φ0.25 m的馬赫數(shù)6 Ludwieg管風(fēng)洞（簡(jiǎn)稱HUSTHLT），如圖21所示。該Ludwieg管風(fēng)洞由雙彎管儲(chǔ)氣段、快開閥、Laval噴管、試驗(yàn)段、擴(kuò)張段和真空罐組成。風(fēng)洞總長(zhǎng)約12 m，占地面積約18 m2；風(fēng)洞每?jī)绍嚧芜\(yùn)行間隔為10 min，每天可以運(yùn)行60次車。

圖21 華中科技大學(xué)高超聲速Ludwieg管風(fēng)洞Fig. 21 Picture of the hypersonic Ludwieg tube tunnel

在對(duì)應(yīng)圖20中x= ?1.2D位置安裝總壓傳感器以測(cè)量Ludwieg管風(fēng)洞運(yùn)行過程中的總壓變化。試驗(yàn)段內(nèi)則采用Pitot探頭齊平安裝XCQ-062 Kulite傳感器。在與數(shù)值模擬相同工況運(yùn)行風(fēng)洞后，將儲(chǔ)氣段和試驗(yàn)段的壓力數(shù)據(jù)記錄下來，并與非定常數(shù)值模擬的數(shù)據(jù)進(jìn)行比較，如圖22所示，可知風(fēng)洞的有效運(yùn)行時(shí)間達(dá)116 ms，與數(shù)值預(yù)測(cè)結(jié)果吻合良好。此外，儲(chǔ)氣段總壓在一個(gè)運(yùn)行周期內(nèi)的最大壓力相對(duì)偏差為0.58%。基于Pitot-Rayleigh關(guān)系，計(jì)算得試驗(yàn)段的來流馬赫數(shù)為6.05，與風(fēng)洞設(shè)計(jì)的名義馬赫數(shù)相對(duì)偏差僅為0.83%。值得留意的是，在數(shù)值模擬中觀察到的壓力波動(dòng)并未發(fā)現(xiàn)，其原因可能是壓力傳感器的精度有限。

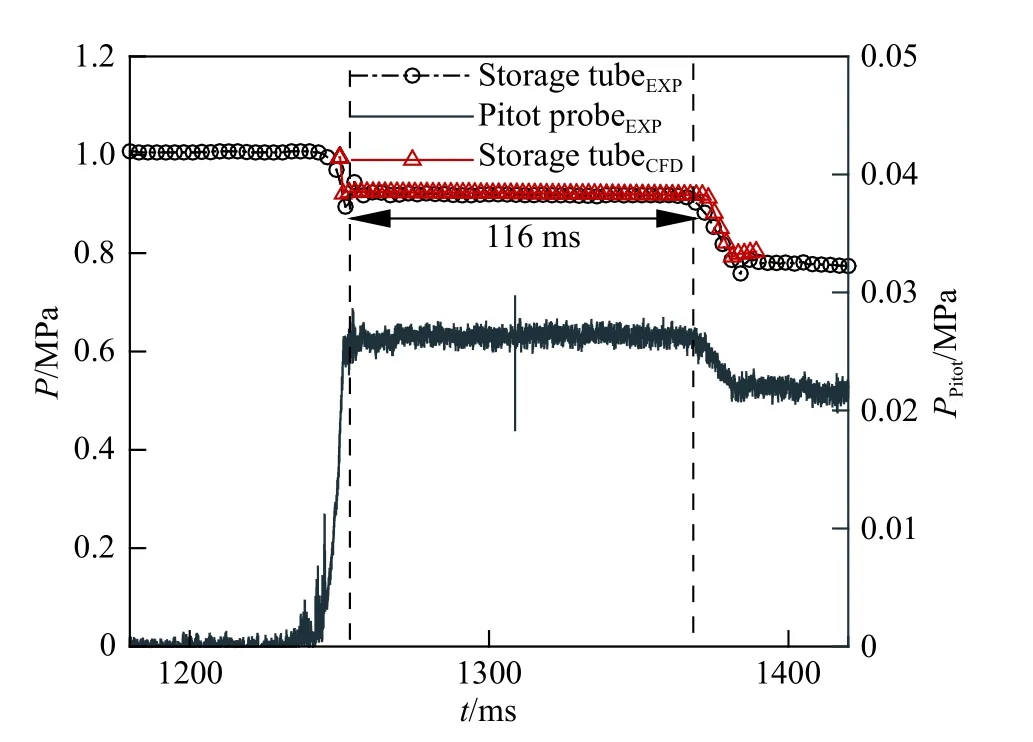
圖22 風(fēng)洞運(yùn)行過程中儲(chǔ)氣段壓力與試驗(yàn)段Pitot探頭壓力變化Fig. 22 Time variation of the pressure in the storage tube and the Pitot probe measured pressue in the test section

最后，采用高速紋影系統(tǒng)對(duì)試驗(yàn)段的Pitot探頭進(jìn)行脫體激波拍攝，以進(jìn)一步確定該Ludwieg管風(fēng)洞的有效運(yùn)行時(shí)間與流場(chǎng)品質(zhì)。相機(jī)的幀速設(shè)置為1000幀/秒，每?jī)煞y影圖片之間的時(shí)間間隔是1 ms。由圖23紋影序列可知，從脫體激波形成到t= 116 ms過程中，Pitot探頭的脫體激波穩(wěn)定，自由來流中無多余的激波與擾動(dòng)，流場(chǎng)品質(zhì)較好。

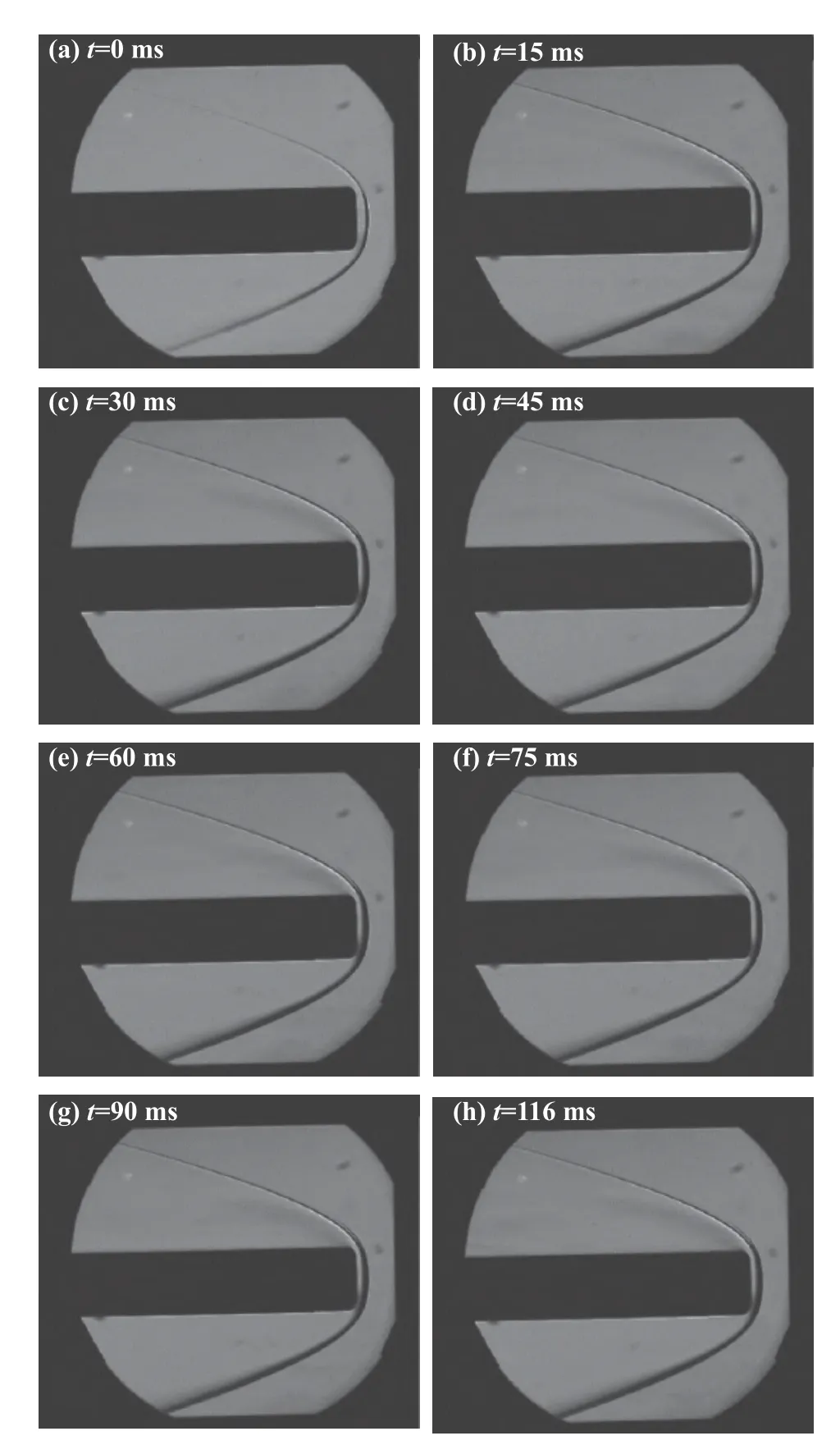
圖23 Pitot探頭紋影圖的時(shí)間序列Fig. 23 Time series of schlieren images of the Pitot probe

5 結(jié)論

本文系統(tǒng)研究了采用一種雙彎管儲(chǔ)氣段布局的高超聲速Ludwieg管氣動(dòng)設(shè)計(jì)，并基于氣動(dòng)設(shè)計(jì)建成Φ0.25 m口徑馬赫數(shù)6 Ludwieg管風(fēng)洞，對(duì)數(shù)值預(yù)測(cè)進(jìn)行了試驗(yàn)驗(yàn)證，初步得出以下結(jié)論：

1）喉部前設(shè)置快開閥將導(dǎo)致Laval噴管出口邊界層增厚近50%，但是對(duì)Laval噴管核心流動(dòng)區(qū)域馬赫數(shù)分布的均勻性影響不大。

2）全Ludwieg管風(fēng)洞非定常數(shù)值模擬結(jié)果顯示，該Ludwieg管風(fēng)洞可在2 ms內(nèi)完成啟動(dòng)，形成高超聲速流動(dòng)；在單個(gè)風(fēng)洞運(yùn)行周期內(nèi)膨脹波在儲(chǔ)氣段逐漸衰減，但是Laval噴管上游的總壓維持不變。

3）儲(chǔ)氣段采用雙彎管布局對(duì)膨脹波的行進(jìn)有一定影響，膨脹波經(jīng)過第二個(gè)彎管時(shí)儲(chǔ)氣段產(chǎn)生微弱的壓力波動(dòng)；在彎管與儲(chǔ)氣段直徑之比為4時(shí)，對(duì)應(yīng)儲(chǔ)氣段壓力波動(dòng)的相對(duì)幅值約為0.04%，雙彎管布局對(duì)流場(chǎng)的影響可忽略不計(jì)。

4）試驗(yàn)測(cè)量風(fēng)洞有效運(yùn)行時(shí)間與數(shù)值預(yù)測(cè)吻合良好，一個(gè)運(yùn)行周期內(nèi)儲(chǔ)氣段壓力相對(duì)波動(dòng)偏差僅為0.58%，但是無法分辨因儲(chǔ)氣段彎曲產(chǎn)生的微弱壓力波動(dòng)；壓力測(cè)量以及Pitot探頭的紋影序列均表明，采用雙彎管儲(chǔ)氣段布局的高超聲速Ludwieg管風(fēng)洞設(shè)計(jì)可行。

以上研究表明，采用雙彎管儲(chǔ)氣段布局的高超聲速Ludwieg管風(fēng)洞，需要合理設(shè)計(jì)彎管與儲(chǔ)氣段直徑比，其流場(chǎng)的品質(zhì)較之采用直管儲(chǔ)氣段布局的情況并無明顯差異。后續(xù)工作將圍繞全流場(chǎng)的高精度數(shù)值模擬與流場(chǎng)的靜態(tài)與動(dòng)態(tài)校測(cè)展開。