帶有截止日期和拒絕的單機總加權誤工量排序問題

趙玉芳, 何欣怡, 陳狀狀

(沈陽師范大學 數學與系統科學學院, 沈陽 110034)

0 引 言

工件有截止日期的約束問題在實際問題中普遍存在[1-3],并且在傳統的排序問題中,都假設每一個工件必須被加工。然而,在現實中決策者為了節省加工成本以獲得更大的利益,會選擇拒絕加工一部分工件而支付一定的費用。張玉忠[4]對工件可拒絕的排序問題進行了綜述。Blazewicz[5]首先提出了誤工量問題,稱其為“信息丟失”,并介紹了極小化總加權誤工量的排序模型。Sterna[6]對早期的誤工量問題進行了綜述。Potts和van Wassenhove[7]證明了單機總誤工量排序問題和單機總加權誤工量排序問題是一般意義NP-難的,并給出了擬多項式動態規劃算法。同年，Potts和van Wassenhove[8]對單機總誤工量排序問題又提出了2個FPTAS(fully polynomial time approximation scheme)算法。Wu等[9]研究了帶有學習效應的總誤工量問題,構造出一個分支定界算法并用遺傳算法得到了近似最優解。對于極小化單機總加權誤工量的排序問題,Kovalyov等[10]對單機總加權誤工量排序問題提出了一個動態規劃算法,并設計了一個FPTAS。Hariri等[11]在上述動態規劃算法的基礎上對這個問題提出了一個算法復雜度為O(n2∑pj)的擬多項式動態規劃算法,對于工件的工期都相同的問題可以在O(n)時間內求解,當工件的加工時間相同時構造了一個算法復雜度為O(n3)的最優算法。Chen等[12]研究了工件具有加工位置上限的總加權誤工量問題,證明了當工件具有相同工期時,問題是一般意義NP-難的,且構造了一個擬多項式動態規劃算法,證明了當工件具有單位權重的時候,問題是強NP-難的。Chen等[1]首次研究了工件有截止日期的問題,證明了帶有截止日期約束且工件工期相同時,總加權誤工量單機排序問題是一般意義NP-難的,并構造了一個擬多項式動態規劃算法和一個FPTAS。

拒絕的概念首先由Bartal等[13]提出,此后得到了學者們的廣泛關注。Engels等[14]研究了帶有拒絕的單機排序問題,目標函數為接受工件的總加權完工時間與拒絕工件的總拒絕懲罰之和,證明了其是NP-難的,并給出了動態規劃算法和FPTAS。Cheng和Sun[15]考慮了帶有退化和拒絕的單機排序問題,目標函數為接受工件的最大完工時間與拒絕工件的總拒絕懲罰之和,證明了該問題是一般意義NP-難的,并給出了擬多項式時間動態規劃算法。國峰和王吉波[16]研究了帶有拒絕工件和學習效應的資源約束排序問題,對線性和凸資源分配函數的2種模型給出了最優求解算法,時間復雜度分別為O(n4)和O(n3)。

本文研究在截止日期的限制下,工件是可拒絕且工期都相同的總加權誤工量與拒絕懲罰之和的單機排序問題。

1 問題描述

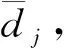
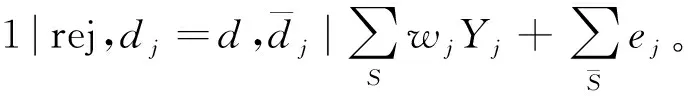
2 可行性檢驗

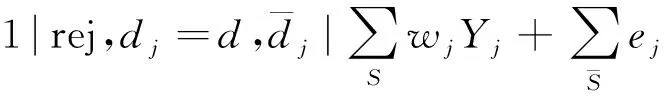
3 主要結論

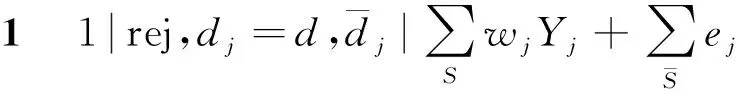
下面構造一個擬多項式算法來求解這個NP-難問題。與文獻[7]和[17]中提出的方法類似,可以通過依次選取關鍵工件或者依次列舉關鍵工件的完工時間,再從所有的可行解中選擇最優解。

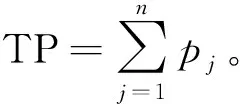
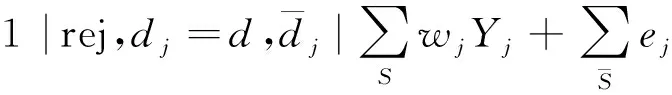
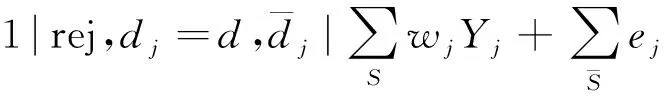
對于問題P(J(c))的可行排序如圖1所示。

圖1 可行排序Fig.1 Feasible schedules

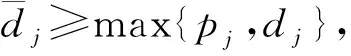
性質1 問題P(J(c))存在一個最優排序,排在J(c)之前的工件從0時刻開始以任意順序連續加工且無空閑時間。

性質2 對于問題P(J(c)),存在一個最優排序σ,排在J(c)之后的工件按截止日期不減的順序排列,即按照它們的下標順序排列。

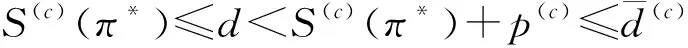
注意到工件Jj共有3種排序情況:

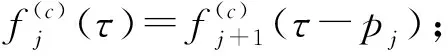
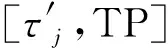
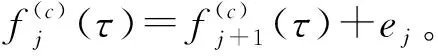
動態規劃算法DP1:

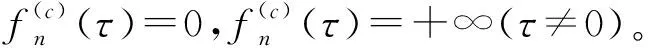
Step 1 對于j∈{1,2,…,n-1}和τ∈{0,1,…,d},有

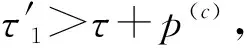
定理2 動態規劃算法DP1的時間復雜性為O(n2d)。

證明 因為j∈{1,2,…,n-1},τ∈{0,1,…,d},Step 1的運行時間為O(nd),Step 2計算函數δ時j最多可以取遍{1,2,…,n-1},運行時間為O(n),因此動態規劃算法DP1在O(n2d)時間內運行。

引理1 問題P(J(c))的最優解為

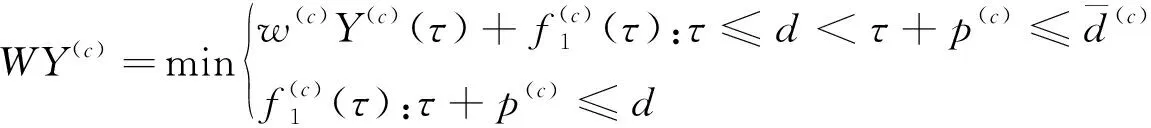
(1)

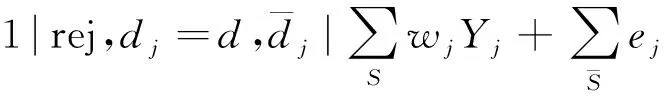
Step 1 將工件按照截止日期的不減順序重新標號。指定J1∈J作為關鍵工件,記為問題P(J(1)),k=1。

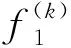
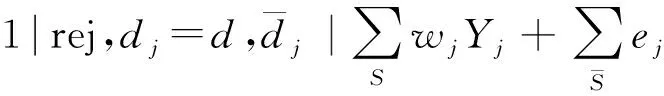
定理3 動態規劃算法DP2的時間復雜性為O(n3d)。

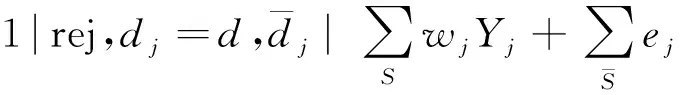
4 數值例子

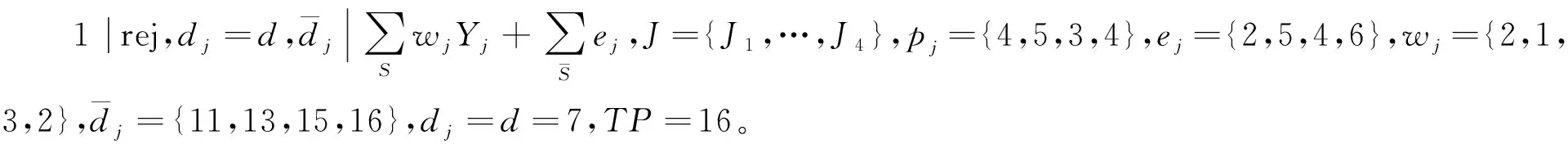
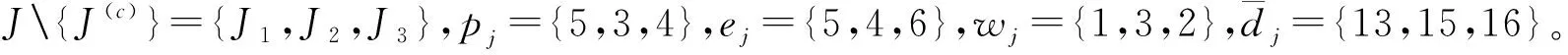
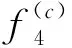
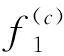
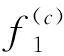
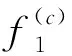
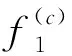
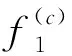
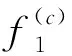
求得WY(c)=9 ,工件排序為{J4,J2,J3,J(c)}或者{J4,J3,J(c)}。

2) 依次選取J2,J3,J4作為關鍵工件的情況同上。

5 結 論

本文研究了帶有截止日期和工件可拒絕的極小化總加權誤工量與拒絕懲罰之和的單機排序問題,該問題是NP-難的,用依次選取關鍵工件的方法構造了一個擬多項式時間動態規劃算法,并證明了該算法的時間復雜度是O(n3d)。對于此問題的后續研究,如考慮不同機器環境下的平行機、恒速機等同一目標函數的其他問題,或者考慮當工件有單位權重時總加權誤工量與拒絕懲罰之和的問題,或研究允許中斷的情況等問題,都值得進一步探討。