10 k W向心透平內二次流形成機理與損失分析

李 鵬， 李 奇， 李國能， 韓 旭， 韓中合

（1.華北電力大學能源動力與機械工程學院，河北保定 071003；2.華北電力大學河北省低碳高效發電技術重點實驗室，河北保定 071003）

有機朗肯循環（ORC）憑借其結構簡單、設備運行維護成本低和循環效率較高等優點，目前已經在低溫余熱回收領域得到廣泛應用［1］。向心透平膨脹機作為循環中的重要部件，其運行效率直接影響整個系統的循環效率。有機工質在向心透平中的流動狀況非常復雜，在動、靜葉通道內流體會表現出以流動分離和多種渦系為主的二次流，二次流損失是工質流動損失的重要部分，研究透平通道中二次流形成機理對透平葉片的改型和氣動性能的提升具有重要意義。

針對透平葉片中二次流現象的理論研究從20世紀50年代就已經開始了，經過大量實驗研究，王仲奇等［2］提出了典型的二次流結構模型。針對不同幾何類型的透平葉片，葉片通道內形成的二次流也有所不同。目前，針對透平內流的研究大多集中在汽輪機和燃氣輪機等軸流透平中。王如根等［3］結合λ2準則模擬了NASA Rotor37轉子中流體的流動，提出了包括馬蹄渦、壁角渦、徑向渦、脫落渦、泄漏渦、誘導渦和分離渦在內的壓氣機轉子內部二次流模型；李相君等［4］模擬了某軸流壓氣機葉柵中的二次流，并推導估算了流場中的損失源，發現二次流對低速流體的間接作用是造成損失的主要原因。Natkaniec等［5］通過CFD建立了商用車徑向渦輪模型，分析發現渦輪定子中除學者發現的入流渦和馬蹄渦外，還有額外的二次渦流；Simpson等［6］通過模擬有無導葉的向心透平內部的流動，分析了兩者透平性能的差異，發現無導葉的透平中高損失主要集中在端壁，在帶導葉的透平上游蝸殼中產生旋向相反的入流渦以及常見的馬蹄渦；李懷志等［7］模擬了向心透平內流在設計工況和非設計工況下的分離和渦系的發展，提出透平葉輪內主要漩渦為馬蹄渦、通道渦和泄漏渦，且通道渦和泄漏渦的交匯和摻混是損失的主要成因；王智等［8］模擬了有機工質在向心透平內的流動，分析了靜葉柵通道以及上下端面渦系的形成情況，研究發現在靜葉柵通道內并未發現通道渦，主要的壓力損失集中在靜葉柵后0.4流向位置的上下端面，且吸力面損失較大。

上述學者針對軸流透平葉柵內部二次流的漩渦結構和損失機理進行了較為細致的研究，相較于軸流透平，針對向心透平內部流動狀態的研究相對較少，且學者研究的重點集中在靜葉柵內部，缺乏向心透平動葉輪中渦系形成和發展的研究，對于整個透平中二次流形成機理和損失的分析并不完善。

筆者以R245fa為工質，對10 k W向心透平進行了詳細的熱力設計和模擬計算，通過對靜葉柵和動葉輪內各種渦系的捕捉和分析，旨在提出向心透平內部完整的二次流結構模型，為后續相關研究提供參考。

1 向心透平設計及三維模型

1.1 向心透平熱力設計

有機工質向心透平的設計原理與一般燃氣或蒸汽透平無異，但工質物性的準確計算是保證透平結構參數設計準確性的基礎。有機朗肯循環透平中的工質分子量大、密度大、音速低，膨脹過程接近飽和線且常為跨音速膨脹［9］，其熱物性與常規工質有顯著區別，不能像空氣或水蒸氣一樣進行完全氣體簡化［10］。為了得到最優的設計結果，基于多目標灰狼優化算法對向心透平進行一維熱力設計。灰狼算法是參照自然界中狼群的狩獵行為而設計的優化算法。參數取自商業物性軟件REFPROP。透平效率計算公式［11-12］如下：

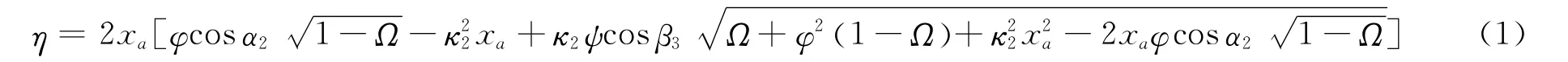
式中：η為輪周效率；φ為噴嘴速度系數；ψ為動葉速度系數；Ω為透平反動度；x a為透平速比；α2為葉輪入口絕對氣流角；β3為葉輪出口相對氣流角；κ2為葉輪輪徑比，是葉輪出口截面中徑dout與入口直徑din之比。

根據向心透平熱力設計流程，如圖1所示，運用灰狼優化算法以透平的輸出功率和輪周效率為目標進行優化，通過Matlab編寫一維熱力設計程序，完成整個透平的設計過程。在滿足透平設計要求的前提下，匹配優化這7個設計參數，使得計算得到的等熵效率與初設的效率在誤差范圍內，輸出該輪周功率下透平相關的幾何參數，見表1。

表1 向心透平幾何參數Tab.1 Radial flow turbine geometry parameters mm

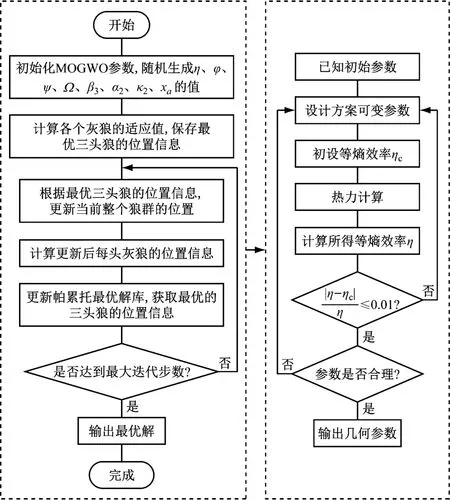
圖1 熱力設計流程圖Fig.1 Thermal design flow chart

1.2 透平模型及邊界條件設置

1.2.1 三維模型及計算網格

根據一維熱力設計得到的透平主要幾何參數，進行導葉柵和動葉輪的選型和造型設計。選用的靜葉柵為莫斯科動力學院研制的TC-4P氣動葉型，該葉型背弧彎曲程度較大，使得葉柵的工況向高馬赫數擴展，且在高馬赫數下的流動損失較小，通常適用于跨音速工況。由于本文所選工質為有機工質R245fa，透平中的馬赫數達到1.0以上，故選用此葉型。動葉輪的造型采用Bladegen，通過設計子午面形狀和葉片進出口角，自動進行動葉輪的設計。葉頂間隙的取值參考文獻［11］和文獻［12］中的取值范圍，軸向間隙取葉輪入口高度的10%，徑向間隙取葉輪出口高度的3%。圖2為靜葉柵和動葉輪的造型圖。

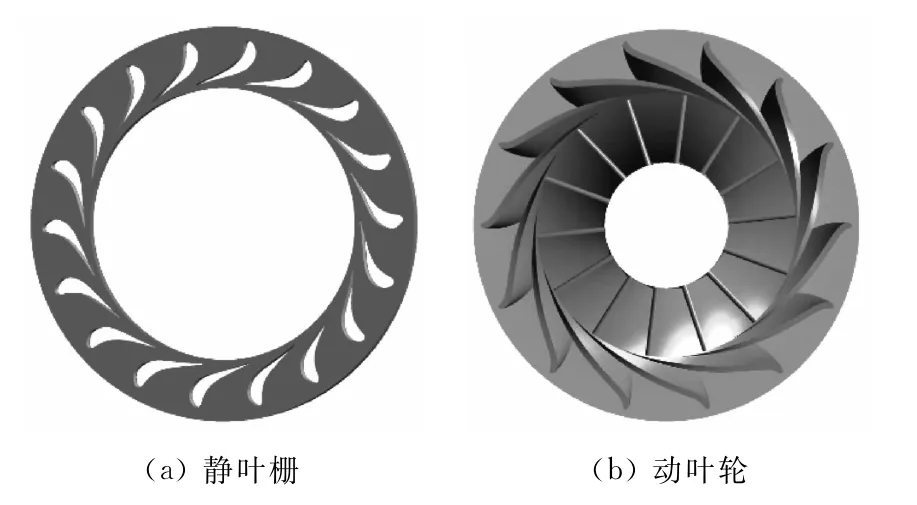
圖2 向心透平三維模型Fig.2 Radial flow turbine 3D models

靜葉柵與動葉輪之間的徑向間隙能夠有效緩解氣流周向方向上的速度脈動，使得進入葉輪的氣流較為均勻。間隙大小的選擇參考文獻［11］中的取值范圍，通常為葉輪入口直徑的4%～8%，根據尺寸要求，選擇葉輪入口直徑的4%。

將動、靜葉模型導入到Turbogrid中進行網格劃分，參考文獻［13］～文獻［15］選擇單流道進行模擬分析，此方法減少了計算網格，可節約計算成本，同時也能得到較為精確的計算結果。經過網格無關性驗證后選取靜葉柵網格數為25.4萬，動葉輪網格數為75.3萬進行計算。圖3為靜葉柵和動葉輪的網格分布情況。

圖3 動、靜葉網格劃分Fig.3 Dynamic and static blade meshing

1.2.2 邊界條件

根據設計工況給定邊界條件。入口邊界條件給定總溫、總壓，出口邊界條件為靜壓。湍流模型選擇SST模型，動靜葉交界面采用stage模式，葉片兩側設置成周期性邊界。設置壓力衰減值為5%，網格連接方式為GGI，選擇穩態求解器進行計算。

1.3 模型驗證

1.3.1 設計方法驗證

為保證上述整個設計過程的正確性，采用上述方法對文獻［16］中的120 k W向心透平重新進行設計，將設計所得透平的相關參數與原文獻進行對比，對比結果見表2。數據顯示，該方法設計結果與文獻基本一致，表明設計方法正確可靠。

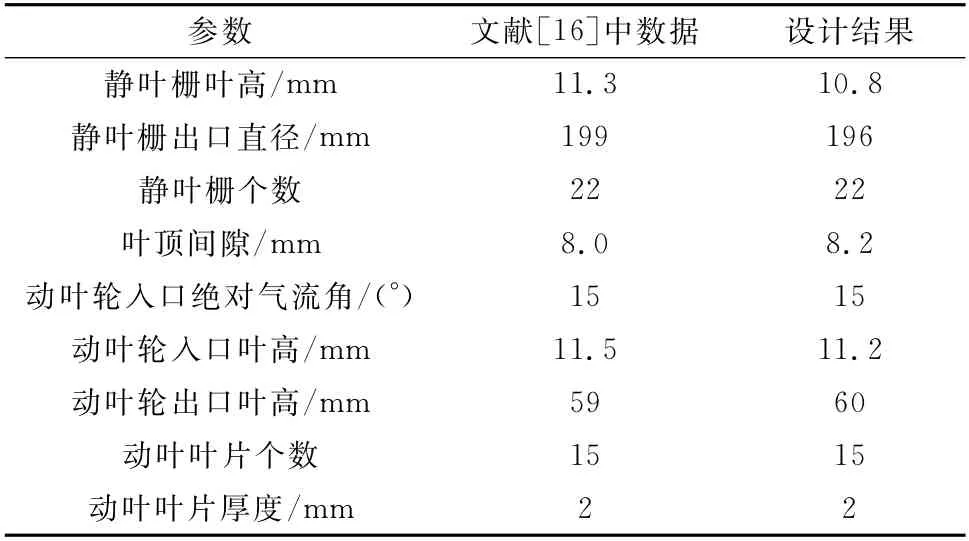
表2 120 k W向心透平設計結果與文獻［16］中數據的對比Tab.2 Comparison between design results of 120 kW radial flow turbine and data in literature［16］

1.3.2 結果驗證

對上述10 k W向心透平進行模擬計算，同時依托學校自行搭建的ORC實驗系統進行實驗驗證，實驗系統如圖4所示。在表3中，將10 k W向心透平的模擬結果和實驗結果與一維熱力設計結果進行對比。從表3中列出的主要參數可以看出：入口壓力、入口溫度和質量流量的結果幾乎沒有誤差；相比之下，透平效率和透平輸出功率的誤差較大，這是由于數值模擬和熱力設計時在工質焓值的計算上存在差異。在熱力設計過程中，工質焓值的計算是在軟件NIST-REFPROP中得到的，利用CFX進行模擬計算時，工質焓值是采用真實氣體狀態方程通過零壓比熱計算得到的。根據文獻［17］，真實氣體狀態方程中溫度的變化對計算結果的影響十分明顯，很小的溫差變化都會造成所計算焓值的較大差異。其次，在模擬計算時進行了一些理想假設，如絕熱和無滑移等，且實際實驗過程中存在人為操作因素和裝置本身氣密性等問題，從而使得計算結果與實驗真實流動的結果存在些許差異。總體來看，設計結果與模擬結果的相對誤差較小，可以認為模擬計算的結果可靠。

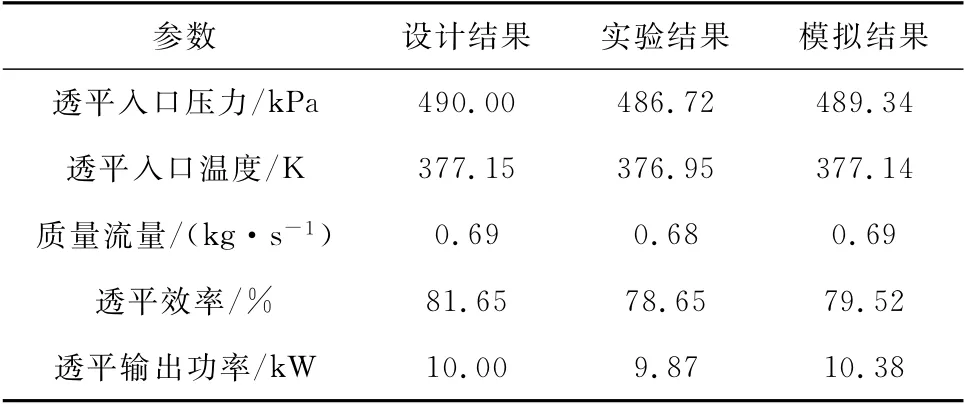
表3 10 kW向心透平模擬結果與設計結果和實驗結果的對比Tab.3 Comparison between simulation results，design results and experimental results of a 10 kW radial flow turbine

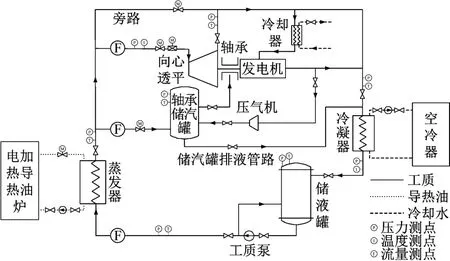
圖4 ORC實驗系統圖Fig.4 Diagram of the ORC experimental system

2 計算結果與分析

2.1 靜葉柵內部二次流及損失

2.1.1 馬蹄渦、通道渦和尾跡渦

流體流經靜葉柵前緣時，由于前緣的阻礙作用，會形成前緣迎流和來流的后方流體之間的逆壓梯度。前緣附近流體在此逆壓梯度作用下反向流動，如圖5所示，在靜葉柵前緣上下端面附近形成沿著根部向周圍發散的分離渦流，使流體不能進入前緣的端面根部區域，在上下端面根部造成類似于馬蹄的渦旋，稱為馬蹄渦。

圖5 靜葉柵壓力側表面流線Fig.5 Pressure side surface streamlines of stator blade

如圖6所示，在上下端面分別形成一個鞍點N，流體經過鞍點之后，分離為兩支分流：N1和N2。第一支分流N1經過前緣，在葉片流道中橫向壓力的作用下流向靜葉柵的吸力面，在距離靜葉柵前緣約1／2弦長的位置與流道中部的來流相匯，之后N1逐漸遠離吸力面。第二支分流N2經過前緣表現出流向靜葉柵壓力面的趨勢，但與N1不同，N2的流線并沒有十分接近葉柵表面，在靠近前緣約1／5弦長位置處，流體在流道中橫向壓差的作用下逐漸遠離壓力面，向吸力面流動。N2在到達吸力面之后并沒有完全消失，其流線分布于之后的整個流道中。

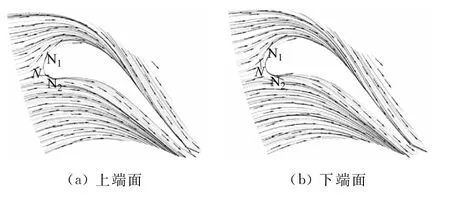
圖6 靜葉柵上下端面流線Fig.6 Upper and lower end face streamlines of stator blade

與汽輪機軸流葉柵不同，在向心透平的葉柵內部不容易形成通道渦［18］。從靜葉柵的型線結構來看，所采用的TC-4P葉柵型線變化平緩，并沒有較大的彎折角度，流線彎曲程度不大，不容易產生離心力。此外，葉柵的弦長較短，通道渦在較短的流道內不容易發展；從實際流動狀況來看，馬蹄渦的壓力面分支一般在弦長1／2之前的位置處到達吸力面，與吸力面分支相匯，在流道的后半段流線分布均勻，不易形成通道渦。

圖7為靜葉柵吸力面流線圖，葉片表面流體在流經前緣之后沿著吸力面向靜葉柵尾緣流動。從吸力面流線圖可以清楚地看到，在葉柵上下端面逐漸發展出2束從前緣流向尾緣的流動分離束，上下端面的流線均逐漸遠離上下端面，向葉柵吸力面中部靠攏，使得吸力面上下端面附近流體不斷向中部補充，加強了吸力面中部流體的流動。由于吸力面流體流動方向與通道渦的旋向相反，對流道中通道渦的發展起到一定的抑制作用。

圖7 靜葉柵吸力面流線Fig.7 Stator blade suction surface streamlines

靜葉柵吸力側和壓力側上下端面角區的低能流體隨著主流向下游流動，在葉柵上下端面的尾緣附近形成如圖8所示的尾跡分離結構。該尾跡區顯現出2個旋向相反、強度不同的尾跡渦對，直觀來看，吸力側上下端面尾緣形成的漩渦較大，結構也相對穩定；但尾跡渦對只存在于上下端面尾緣附近，在葉柵尾緣中部的尾流中不會觀察到類似的尾跡渦對。

觀察圖8（a）～圖8（c）可知，隨著截面高度的增加，葉柵下端面附近的尾跡渦對強度逐漸減弱，漩渦核心變小，逐漸被主流帶走；在0.03靜葉高截面（即所取截面高度為0.03倍的靜葉柵高度）流線處，圖8（d）壓力側尾緣的漩渦消失，吸力側的尾跡渦并未完全消失，在近壁面仍能觀察到一個尺度很小的渦；如圖8（e）和圖8（f）所示，流線疏密程度相同的情況下，在0.04靜葉高截面基本觀察不到尾跡渦，在0.05靜葉高截面尾跡渦完全消失。下端面尾跡渦的發展狀況與上端面相似，觀察圖8（i）和圖8（j）可知，2個尾跡渦的尺度逐漸變小，同樣靠近吸力側的尾跡渦強度較大；在0.97靜葉高截面流線觀察到壓力側的漩渦基本消失，在吸力側近壁面同樣還存在微小漩渦；如圖8（g）和圖8（h）所示，越靠近尾緣中部，尾跡渦的核心逐漸變小，到0.95靜葉高截面完全消失。

圖8 靜葉柵不同葉高截面流線分布Fig.8 Streamline distributions in different blade height sections of stator blade

2.1.2 靜葉柵內損失分析

采用靜壓利用系數Cp來反映靜葉柵內部的總壓損失。

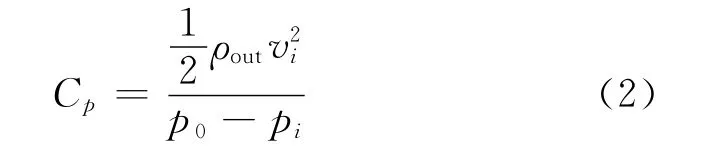
式中：p0為入口總壓；p i為靜葉出口任意截面的壓力；ρout為出口工質的面平均密度；v i為靜葉柵出口工質在任意截面的平均速度。

圖9給出了靜葉柵不同截面的靜壓利用系數沿葉高方向的分布情況。0.6弦長截面是指距離靜葉柵前緣0.6弦長位置的截面，其余截面同理。由圖9可知，靜葉柵的靜壓利用系數在靠近上下端面處較小，并以0.5葉柵高度為中心呈對稱分布；同時，各截面的靜壓利用系數沿流向增大，0.8弦長截面和0.9弦長截面以及出口截面的靜壓利用系數均在約0.2和0.8葉高的位置出現明顯降低。

圖9 不同截面的靜壓利用系數沿相對葉高的分布Fig.9 Distribution of static pressure utilization coefficient along blade height in different sections

上述靜壓利用系數分布的原因是在流道的中后段上下端面角區存在低能流體，使得葉柵尾緣出現上述尾跡渦對，造成流動損失；同時，工質在流道的中后段充分膨脹，圖10（a）和圖10（b）分別給出了葉柵尾緣的總壓分布和速度分布狀況，可以清楚地觀察到吸力面邊界層的加厚和脫離現象，這也會造成相應的流動損失。因此，靜葉柵內部的損失主要集中在喉部之后的上下端面以及尾緣附近。

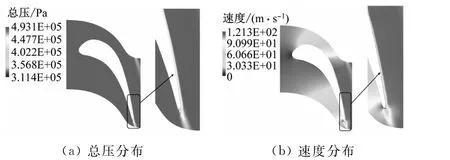
圖10 靜葉柵尾緣總壓和速度分布Fig.10 Total pressure and velocity distribution of the trailing edge of the stator blade

2.2 動葉輪內部渦系及損失

2.2.1 前緣壓力渦、通道渦和間隙泄漏渦

圖11為動葉輪入口前緣附近不同截面的流動情況。流體在靜葉柵中膨脹加速后，靜葉柵出口處的流速將達到超音速，在經過動葉前緣時，由于動葉前緣安裝角度的原因，會造成較大的沖擊損失，流體在動葉壓力側底部形成2個低速漩渦；同時，由動葉前緣端壁發展起來的通道渦會與這2個低速渦旋相交，形成2個如圖11（a）所示的流束。與低速渦旋疊加后的通道渦隨著流體向流道后方運動，同時由于動葉流道高度的增加，動葉流道中的通道渦也隨著葉高的增加而上升。如圖11（b）～圖11（d）所示，壓力側底部的低速渦旋隨著葉高的增加，其漩渦中心逐漸變小，周圍的低速流體逐漸被主流帶走。如圖11（e）和圖11（f）所示，隨著動葉高度的增加，前緣壓力側的2個低速渦旋的范圍繼續變小，動葉流道內的流動狀況逐漸趨于理想狀態，如圖11（g）所示，在0.6動葉高度截面（即動葉高度的0.6倍處取得的截面）時，前緣壓力側低速渦旋的影響雖然未完全消失，但流道中的流動狀態為所有截面中最佳。在動葉前緣端壁發展起來的通道渦隨著主流向動葉出口移動，并隨著葉高的增加逐漸被抬升，在0.7動葉高度截面，通道渦在接近動葉尾緣壓力側時逐漸顯現出來，在流道的中后段出現了流動分離，如圖11（i）所示，通道渦在此截面流道內充分發展，尺度逐漸變大，同時加之動葉片的中后段扭曲程度較大，使得流道中部的流動分離現象加劇，從主流分離出的一部分流體向葉片吸力面靠近，剩余部分與通道渦一起向壓力面移動。由于入口動葉和靜葉柵存在一定的高度差（動葉入口略高于靜葉柵），在靠近動葉頂部的0.9靜葉高截面，動葉入口流線方向與前幾個截面入口流線方向不同，其流動方向與葉輪旋轉方向相切。如圖11（j）所示，在動葉頂部由于還存在葉頂間隙，使得動葉頂部葉片的邊界層流體向間隙中流動。從圖11（k）可以看出，流體會從壓力面經過葉頂間隙流向附近的1個流道中，在動葉入口附近，由于葉頂間隙造成的壓力差和流道中橫向壓力的共同影響，在壓力側入口附近形成1個向葉頂間隙和臨近葉片吸力側發散流動的流束，使得頂部截面的流動狀態更為復雜。

圖11 動葉不同葉高截面流線Fig.11 Different leaf high-section streamlines of the rotor

2.2.2 動葉輪內部損失分析

為了準確描述動葉輪內的流動損失狀況，如圖12所示，沿著流向截取5個垂直動葉輪子午流線的截面，截取位置分別為動葉前緣到尾緣距離的0%、25%、50%、75%和100%。分析各個截面上的總壓分布狀況。

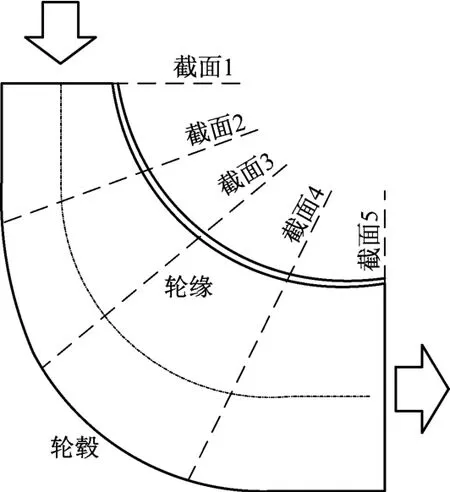
圖12 流道截面示意圖Fig.12 Schematic diagram of the flow passage section

圖13給出了動葉不同截面的總壓分布。截面1的流動狀態顯示，在動葉前緣截面中部主流區的總壓分布均勻，且工質從壓力面流向吸力面；在吸力面附近存在部分與主流流向相反的流動，二者交匯之后流向頂部間隙。在交匯區域附近的總壓比主流區總壓小，說明此處會造成一部分總壓損失，但程度不大。截面2的流動狀態顯示，分別在壓力面底部角區和吸力面頂部存在漩渦，頂部的泄漏渦渦核尺度大，且在泄漏渦所在區域的總壓明顯低于其他區域，說明吸力面頂部的泄漏渦會造成較為明顯的總壓損失［19］。截面3中隨著葉高的增加，葉頂間隙增大，此時泄漏渦的尺度也變大，由泄漏渦造成的總壓損失的范圍和程度均增加。與截面2和截面3相比，截面4的流動狀況較好，原本靠近葉頂總壓損失較大的區域范圍變大，總壓損失核心的位置下移，其壓力值比截面3總壓損失核心處的壓力大，表明截面4的總壓損失程度較小。泄漏渦和通道渦的相互交匯和摻混使得截面5的流動狀況較差，在壓力面中上部產生了流動分離和多個漩渦，這也是造成損失的主要原因。

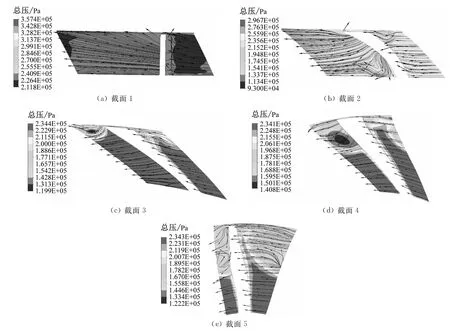
圖13 不同截面總壓分布云圖Fig.13 Cloud map of total pressure distribution in different cross-sections

3 結 論

（1）工質在靜葉柵前緣形成馬蹄渦，鞍點N之后分為N1、N22股分流，在靜葉柵通道內并未發現通道渦，尾跡渦成對出現在靜葉柵尾緣的上下端面，旋向相反，吸力側尾跡渦的尺度較大。動葉輪中的渦系形式主要有前緣壓力渦、通道渦和泄漏渦。在前緣壓力側存在2個低速漩渦，此處端壁發展起來的通道渦會與之交匯摻混，在0.6靜葉高截面前緣，低速漩渦的影響消失，但通道渦仍存在；在0.9靜葉高截面泄漏渦顯現出來，與通道渦相互影響，使得葉頂附近截面的流動狀況變得復雜。

（2）靜葉柵各個截面的總壓損失系數在上下端面較大，且以0.5葉高為中心呈對稱分布，0.7弦長截面（喉部截面）之后總壓損失分布集中，較0.6弦長截面明顯增大，故靜葉柵內部的損失主要發生在喉部之后的上下端面及尾緣。

（3）動葉不同截面的總壓分布顯示，動葉中的總壓損失主要集中在葉頂間隙附近區域，隨著動葉高度的提升，總壓損失范圍逐漸增大。由動葉前緣端部發展起來的通道渦與泄漏渦的相互交匯和摻混是造成動葉損失的主要原因。