一種適用于大體積弱磁材料磁導率測量的方法

嚴勤，李世松，葉遠譽，熊志凌，趙偉，熊茹

(1.國網江西省電力有限公司，南昌 330077； 2.清華大學 電機系，北京 100084；3.國網江西省電力有限公司供電服務管理中心，南昌 330013)

0 引 言

磁導率是磁性材料的基本電磁特性，它反映著磁性材料的導磁能力。磁性材料一般分為高導磁材料和弱磁材料。高導磁材料的相對磁導率大于100，如微晶材料，其相對磁導率可達104～105，一般應用于電磁能量變換、磁屏蔽、傳感器等領域[1-3]。而弱磁材料的相對磁導率較低，多應用在不希望出現磁參量的場合或領域，例如采用電磁方法對金屬砝碼的質量進行測量和校準[4-5]，其中，所使用的不銹鋼砝碼材料的相對磁導率雖然已很低，典型值如1.02(E1級砝碼)至1.8(F2級砝碼)，但其對砝碼質量的最終測量結果仍會造成較大影響，仍然需要再進行準確性評估[6-7]。

對高導磁材料磁導率的測量，方法已比較成熟，最常采用的測量方法，是將被測高導磁材料加工成一個固定尺寸的圓環形磁芯，利用類似變壓器的設計，設置激勵線圈和感應線圈(開路)，通過測量激勵電流與感應電壓之間的關系，確定出該被測高導磁材料的BH曲線，繼而再確定其磁導率的量值[8-10]。

而對弱磁材料磁導率的測量，根據國家標準GB/T 35690-2017[11]，主要的測量方法包括有螺線管法、磁矩法及磁天平法等。具體地，螺線管法和磁矩法的基本原理，是將固定尺寸的被測弱磁材料樣品放置在一個感抗可溯源的線圈中，通過測量放入弱磁材料樣品后線圈的感抗值或磁通量變化，來確定被測弱磁材料的磁導率值。而磁天平法，則是將被測弱磁材料樣品放置在已知的梯度磁場中，通過測量電磁力的變化，去確定弱磁材料的磁導率[12]。文獻[13]提出了一種利用開氣隙的磁芯來測量弱磁材料磁導率的方法，可以測量與氣隙尺寸對應的弱磁材料樣品的磁導率。上述測量方法的主要缺點是對被測弱磁材料樣品的尺寸有嚴格要求，需要對測測弱磁材料樣品進行相應的機械加工和處理(如切割等)。然而，弱磁材料樣品的磁導率對機械加工比較敏感，由此引入的應力、材料成分等屬性變化，會致使加工后弱磁材料樣品的磁特性與原材料的弱磁特性存在較大差別，因而就會導致測得結果與實際材料磁導率之間存在較大差別。

為解決上述問題，文中提出一種基于端部開放式的磁路設計的方法，來測量大體積弱磁材料的磁導率。所提出測量方法的特點在于，僅通過與被測弱磁材料樣品表面接觸，而無需對被測弱磁材料進行任何機械加工及處理，就可以測量出該弱磁材料的磁導率。文中研究論證所提出測量方法的基本原理和數學模型，并采用有限元仿真分析計算方法，對所提出測量方法的合理性和可行性進行驗證，同時探討可能的主要誤差來源。

1 測量方法和數學模型

所提出的弱磁材料磁導率測量方法的實現原理，如圖1所示，其中，主磁軛(后簡稱“磁軛”)利用高磁導率電工材料(如電工鋼)制成，采用U字形設計，且磁軛的兩端處在同一水平面上。磁軛上纏繞有兩個線圈，即一個激勵線圈和一個檢測線圈。激勵線圈共N1匝，通以幅值為I1、頻率為f的低頻正弦激勵電流，用于產生激勵磁場。檢測線圈共有N2匝，用于測量感應電壓，亦即磁場強度。為減小漏磁場對測量結果的影響，兩個線圈均繞制在U型磁軛的底端，如圖1所示。

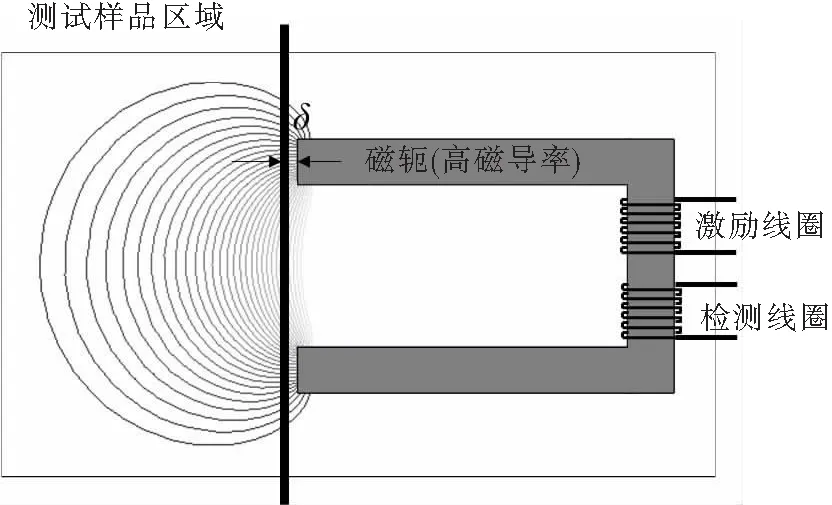
圖1 弱磁材料磁導率測量原理圖

實施測量時，將U型磁軛的兩端緊貼在被測弱磁材料上。考慮到磁軛與被測弱磁材料之間很難做到完美貼合，會存在一個很小的氣隙，設該氣隙的寬度為δ。基于上述條件，根據磁路的歐姆定律，由被測弱磁材料與磁軛所構成的整體磁路滿足的磁動勢方程，可寫成：

(1)

式中l為磁軛的總長度；S代表磁軛的截面積，d是被測弱磁材料樣品中磁通的等效路徑長度；φ表征經過檢測線圈的磁通量；μ、μ0和μm分別為磁軛材料、空氣和被測弱磁材料的磁導率。需要注意的是，l中包含了漏磁場所導致的等效長度變化。

因弱磁材料的磁導率與空氣的磁導率很接近，且磁軛材料的磁導率遠大于μ0，故磁路中主要的磁動勢會落在被測弱磁材料樣品的兩側，因此式(1)中等號左邊的第一項可被略去。定義μm=(1+ε)μ0，則磁軛中的磁通量可表示為：

(2)

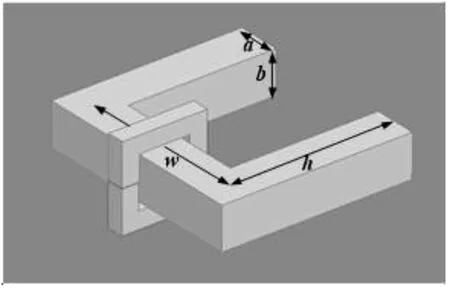
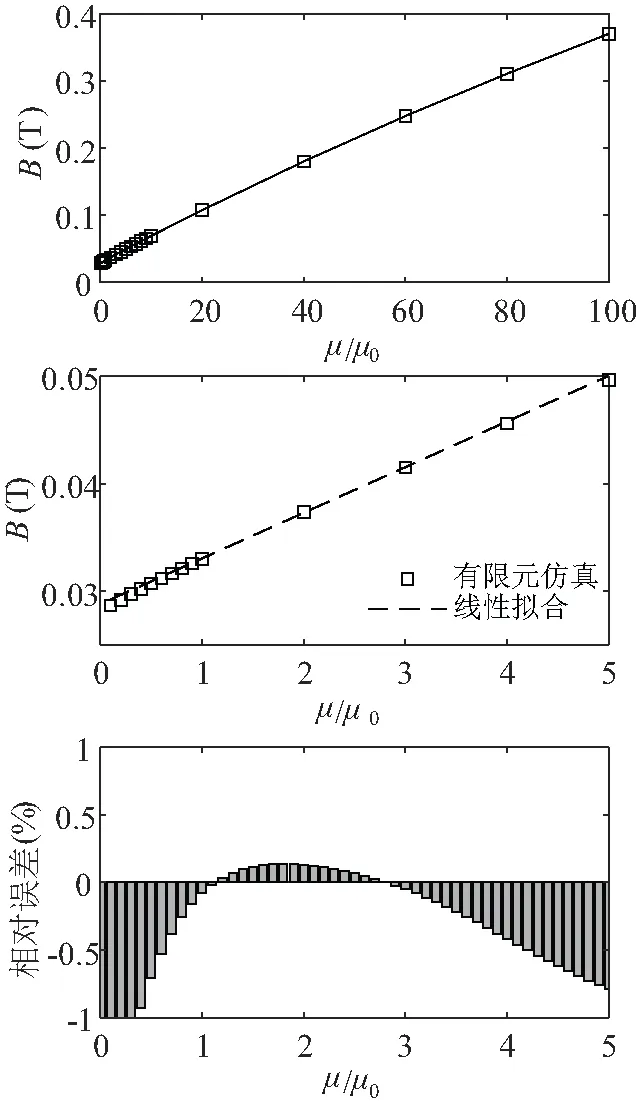
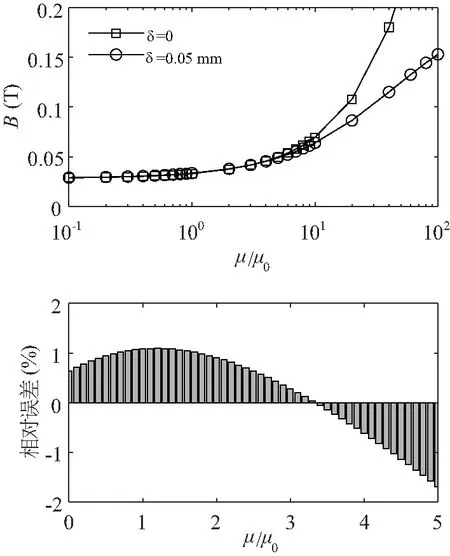
實際測量中，氣隙δ<

(3)

根據法拉第電磁感應定律，在檢測線圈中檢測到的感應電壓信號為：

(4)

原則上，已知線圈參數(N1、N2)、被測弱磁材料樣品中磁通的等效路徑長度(d)、磁軛截面積(S)以及激勵電流幅值(I1)，就能將被測弱磁材料樣品的磁導率測量出來。但是，按上述測量原理直接實施測量并不容易，因為存在如下困難：(1)對上述公式中相關參數的測量，特別是對幾何參數的高準確度測量并不容易，而且有的參數還可能會隨時間或測量條件的改變而發生變化；(2)磁路中存在較嚴重的邊緣效應，且該效應與氣隙的相對尺寸有關，在實際測量中必須予以考慮。針對于此，這里提出采用一種計量學上常用的所謂“替代法”，旨在規避上述問題。具體地，擬測量如下定義的幾何因子，即：

(5)

如此，式(4)可以改為如下形式：

U=Gμm

(6)

采用“替代法”，就要在測量中增加一個步驟，即移除被測弱磁材料樣品，則磁路變為由磁軛以及空氣所構成；鑒于弱磁材料的磁導率與空氣的磁導率很接近，故可認為磁路長度不變；仿前，再利用磁軛材料的磁導率遠大于μ0的條件，于是，磁軛中的磁通量可近似表示為：

(7)

此條件下，檢測線圈上獲得的感應電壓信號為：

(8)

比較、聯立式(6)和式(8)，不難得到被測弱磁材料樣品的相對磁導率為：

(9)

由式(9)可以看出，通過采用“替代法”，可將對弱磁材料磁導率的測量，轉化為對兩個感應電壓信號比例的測量，測量的效率和準確性均可大幅提高，并且還能夠消除氣隙附近磁場的邊緣效應。

2 仿真分析和討論

為了驗證所提出的弱磁材料磁導率測量新方法的有效性，采用有限元仿真軟件，對上述數學模型進行了數值計算和分析。具體地，在有限元仿真軟件環境中構建了如圖2所示的3D檢測磁路，設置：U型磁軛高度h=20 mm，底部寬度w=20 mm，磁軛的截面積S=25 mm2(a=b=5 mm)；磁軛材料的相對磁導率為10 000；被測弱磁材料是100 mm×100 mm×100 mm的立方體；激勵電流為幅度等于10 A、頻率是1 Hz的低頻正弦電流。

圖2 有限元仿真模型參數

首先，仿真計算理想測量條件下，即磁軛與被測弱磁材料之間無氣隙(δ=0 mm)時，檢測線圈輸出的感應電壓信號隨被測弱磁材料磁導率變化的函數關系。為了更直觀地觀察測量結果，仿真計算中采用檢測線圈位置處磁芯中的磁感應強度B作為監測信號。由式(4)可知，該監測信號是與檢測線圈輸出感應電壓信號成正比的(B=φ/S)。

為了在較大范圍觀察B隨磁導率的變化，將被測弱磁材料的相對磁導率μr設置為0.1～100。有限元仿真計算所得的B為隨時間變化的正弦曲線，其幅值隨μr變化的函數關系如圖3所示。

圖3 磁芯中磁感應強度隨μr變化的曲線

仿真計算結果顯示出，當μr>10時，檢測輸出信號表現出較明顯非線性，這主要是由磁軛磁阻的非線性所導致的，因為當μr的值增大時，式(1)中等號左側第一項與后兩項相比，已經不能忽略不計。圖3中還給出了μr從0.1～5區間內，B-μr之間滿足較好的線性關系；不難看出，其線性度在μr取值在0.5～4區間內優于0.5%。

在對數學模型的分析中認為，磁軛與被測弱磁材料樣品之間接觸的氣隙δ相對于d而言可以忽略不計。而精細化的模型中，應該考慮該氣隙所帶來的測量誤差。為了評估氣隙對測量結果的影響，在有限元仿真分析計算中增加了一種情形，即δ= 0.05 mm。B-μr在δ= 0和δ= 0.05 mm下的仿真結果如圖4所示。

圖4 磁軛與被測弱磁材料樣品之間氣隙對測量結果的影響

從仿真計算結果可以看出，考慮氣隙δ時，在高值μr范圍內(μr>5)，測量結果與氣隙為0條件下的差值，會隨著被測弱磁材料磁導率的增加而變大。這是因為，隨著被測弱磁材料磁導率的增加，式(1)中等號左側第二項，即氣隙磁阻項，相對于第一項(磁軛磁阻)和第三項(被測弱磁材料樣品磁阻)所占的比例會增加；而當被測弱磁材料的磁導率與μ0接近時，例如μr∈(0.1,4)，兩測量結果之間的差值小于1%。

最后，再對所提出測量方法的頻率特性做如下分析。在上述仿真分析計算中，采用的是1 Hz的激勵電流信號，而在其他頻率激勵電流下對被測弱磁材料磁導率量值的確定，只需要改變激勵電流的頻率，并調整檢測線圈的匝數即可。而對弱磁材料直流磁導率的確定，則可采用文獻[6]中提出的頻率外推法，即通過在低頻范圍擬合μr-f之間的函數關系，進而確定在豎直軸(μr)上的截距即是。

綜上所述，有限元仿真計算結果證實了，在弱磁范圍內，所提出的磁導率測量方法，的確能夠線性地反映被測弱磁材料磁導率的變化。在合理控制測量中存在的磁軛與被測弱磁材料樣品之間接觸氣隙前提下，能獲得百分位上的測量準確性。

3 結束語

針對傳統弱磁材料磁導率測量方法，對被測弱磁材料樣品的尺寸有限制、需要機械加工處理，從而會導致被測弱磁材料樣品磁特性改變的問題，提出了一種適合大體積弱磁材料磁導率測量的新方法。該方法采用一種簡單的磁路設計，通過實施“替代法”，可避免對感抗參數的測量，能夠較準確地測定被測弱磁材料樣品的磁導率。

文中通過磁路分析，建立了所提出弱磁材料磁導率測量方法的數學模型。基于有限元仿真分析計算，對所提出方法的數學模型進行了有效性驗證，并對磁軛與被測弱磁材料樣品之間氣隙給測量造成的誤差等進行了分析。仿真計算結果顯示出，在氣隙為0.05 mm條件下，可基于該方法在相對磁導率為(0.5,4)范圍內，實現對弱磁材料磁導率在10-2量級準確性的測量。