面向特征繼承性增減的在線分類(lèi)算法

劉兆清 古仕林 侯臣平

(國(guó)防科技大學(xué)文理學(xué)院 長(zhǎng)沙 410073)

由于現(xiàn)實(shí)環(huán)境的開(kāi)放性與復(fù)雜性，在許多實(shí)際應(yīng)用中，人們不得不面臨數(shù)據(jù)的數(shù)量與特征維度都在同時(shí)變化的情形.一個(gè)典型的場(chǎng)景就是數(shù)據(jù)當(dāng)前的特征增加，下一時(shí)刻的數(shù)據(jù)特征只有部分被繼承，并且由于環(huán)境變化難以預(yù)知，哪些特征會(huì)消失、哪些特征會(huì)被繼承難以提前確定.本文將這樣的數(shù)據(jù)稱(chēng)為特征繼承性增減的流式數(shù)據(jù).例如，在環(huán)境監(jiān)測(cè)任務(wù)中，任意時(shí)刻環(huán)境中都存在著多種不同壽命的傳感器，每個(gè)傳感器的反饋均被視為一個(gè)特征[1]，不同特征因?yàn)閭鞲衅鲏勖煌S持的時(shí)間也不同.在壽命較短的傳感器失效之前，為維持對(duì)環(huán)境的觀察，會(huì)向環(huán)境投放新的傳感器，使得在某個(gè)較短的時(shí)期內(nèi)數(shù)據(jù)會(huì)包含歷史特征與新增特征；當(dāng)這部分壽命較短的傳感器失效后，其對(duì)應(yīng)的特征隨即消失，而壽命較長(zhǎng)的傳感器對(duì)應(yīng)的特征將繼承到下一時(shí)刻.總體來(lái)說(shuō)，這是一個(gè)特征先進(jìn)行增加，然后有繼承地減少的過(guò)程.

具體地，如圖1所示：在T1的初始階段(綠色部分)，環(huán)境中存在2種傳感器，返回的數(shù)據(jù)具有特征S1與S2；在b1階段，新一批傳感器被部署在環(huán)境中，數(shù)據(jù)中新增特征S3，此時(shí)數(shù)據(jù)中共包含3種特征，稱(chēng)為過(guò)渡階段；在T2的初始階段(藍(lán)色部分)，第1批傳感器到達(dá)使用壽命之后被銷(xiāo)毀，其對(duì)應(yīng)的數(shù)據(jù)特征S1隨即消失，此時(shí)數(shù)據(jù)特征僅剩繼承自上個(gè)階段的S2與S3，在b2階段，又有一批新的傳感器被部署在環(huán)境中，數(shù)據(jù)中又會(huì)出現(xiàn)新的特征S4.在現(xiàn)實(shí)場(chǎng)景中，數(shù)據(jù)流的特征將隨時(shí)間不斷增加或減少，但由于傳感器壽命的差異性，上一時(shí)刻數(shù)據(jù)的特征總有一部分會(huì)繼承到下一時(shí)刻，因此我們將其定義為特征繼承性增減的流式數(shù)據(jù).

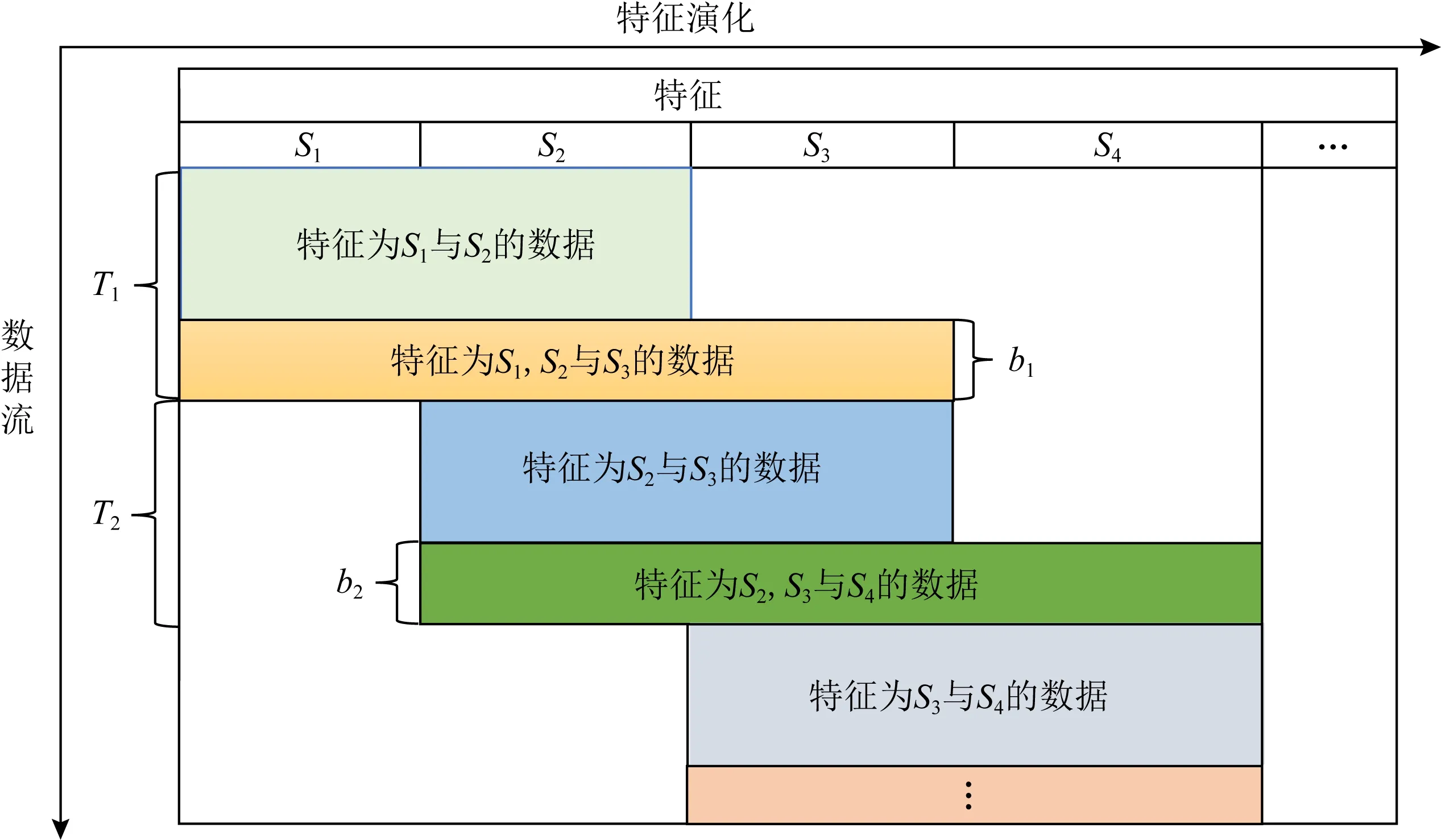
Fig. 1 The feature evolution pattern of environment monitoring圖1 環(huán)境監(jiān)測(cè)任務(wù)中特征的演化規(guī)律

傳統(tǒng)的在線學(xué)習(xí)算法要么假設(shè)數(shù)據(jù)以流的形式依次到達(dá)但是其特征空間保持不變[2-7]，要么假設(shè)特征以流的形式不斷到達(dá)但是訓(xùn)練數(shù)據(jù)集保持不變[8-13]，這些都無(wú)法直接用于處理特征繼承性增減的流式數(shù)據(jù).解決該問(wèn)題一個(gè)簡(jiǎn)單直接的方法是只利用具有相同特征空間的數(shù)據(jù)進(jìn)行模型訓(xùn)練，但是這樣并不能取得好的預(yù)測(cè)效果，主要原因有2個(gè)：1)部分特征消失后，消失特征對(duì)應(yīng)的權(quán)重?zé)o法繼續(xù)利用，在過(guò)去的迭代過(guò)程中從樣本中提取的信息被浪費(fèi)，產(chǎn)生了信息的損失；2)在新特征出現(xiàn)的初始階段，具有新特征的樣本數(shù)量少，不足以充分訓(xùn)練分類(lèi)器，對(duì)分類(lèi)器的性能造成影響.

解決特征動(dòng)態(tài)變化這一問(wèn)題的關(guān)鍵就是建立一個(gè)能盡可能多地繼承原有信息的動(dòng)態(tài)分類(lèi)模型.基于上述思想，近年來(lái)有極少部分工作針對(duì)動(dòng)態(tài)特征的場(chǎng)景進(jìn)行了研究[14-16].這些工作采用不同的特征劃分或投影策略來(lái)構(gòu)建動(dòng)態(tài)模型，在處理特征動(dòng)態(tài)變化的問(wèn)題上做出了原創(chuàng)性的貢獻(xiàn).但是，上述工作假設(shè)的數(shù)據(jù)特征演化方式與本文都不相同，因此相關(guān)的技術(shù)挑戰(zhàn)和解決方法也各不相同.

針對(duì)特征繼承性增減的流式數(shù)據(jù)分類(lèi)問(wèn)題，本文提出了一種面向特征繼承性增減的在線分類(lèi)算法(online classification algorithm with feature inheritably increasing and decreasing, OFID)及其2種變體OFID -Ⅰ和OFID -Ⅱ.當(dāng)新特征出現(xiàn)時(shí)，OFID引入新權(quán)重對(duì)其進(jìn)行學(xué)習(xí)，對(duì)原始特征與新增特征上的分類(lèi)器制定不同的更新策略，通過(guò)結(jié)合在線被動(dòng)-主動(dòng)(online passive aggressive algorithms, PA)算法[5]與結(jié)構(gòu)風(fēng)險(xiǎn)最小化原則分別更新原始特征與新增特征上的分類(lèi)器；當(dāng)部分原始特征消失時(shí)，利用歷史數(shù)據(jù)與當(dāng)前數(shù)據(jù)的一致性，運(yùn)用在線矩陣補(bǔ)全的方法，對(duì)數(shù)據(jù)流的缺失部分使用Frequent-Directions算法[17-18]進(jìn)行恢復(fù)，使得原始分類(lèi)器得以繼續(xù)更新迭代；為防止出現(xiàn)過(guò)擬合現(xiàn)象，開(kāi)發(fā)了OFID算法的2種軟間隔變體OFID -Ⅰ和OFID -Ⅱ.理論分析和實(shí)驗(yàn)結(jié)果分析都驗(yàn)證了本文所提算法的有效性.

本文工作的創(chuàng)新點(diǎn)總結(jié)有3個(gè)方面：

1) 研究了一個(gè)對(duì)特征繼承性增減的數(shù)據(jù)流進(jìn)行分類(lèi)的新問(wèn)題，這一問(wèn)題具有重要的實(shí)際應(yīng)用價(jià)值，對(duì)該問(wèn)題進(jìn)行專(zhuān)門(mén)的研究.

2) 設(shè)計(jì)了一種新穎的算法OFID及其2種變體OFID -Ⅰ和OFID -Ⅱ，從特征繼承性增減的數(shù)據(jù)流中學(xué)習(xí)高度動(dòng)態(tài)的分類(lèi)模型.從理論上證明了OFID系列算法的損失上界，保證了算法的可靠性與有效性.

3) 通過(guò)對(duì)比實(shí)驗(yàn)，在公開(kāi)數(shù)據(jù)集上與其他算法進(jìn)行了對(duì)比，并取得了良好的表現(xiàn)；同時(shí)通過(guò)另外2組輔助實(shí)驗(yàn)探究了算法的參數(shù)敏感程度與時(shí)間復(fù)雜情況，驗(yàn)證了算法自身的良好性質(zhì).

1 相關(guān)工作

針對(duì)特征動(dòng)態(tài)變化的在線學(xué)習(xí)研究在實(shí)踐上具有廣泛的應(yīng)用前景，例如環(huán)境監(jiān)測(cè)、垃圾郵件識(shí)別等.本文致力于研究面向特征繼承性增減的在線學(xué)習(xí)方法，主要包含2個(gè)方面：1)在線學(xué)習(xí)；2)特征動(dòng)態(tài)變化.下面我們將從這2個(gè)方面對(duì)本文的相關(guān)工作進(jìn)行概述.

在線學(xué)習(xí)的研究經(jīng)歷了較長(zhǎng)時(shí)間的發(fā)展，具有成熟的理論與巨大的應(yīng)用價(jià)值[13]，期間發(fā)展出許多經(jīng)典的方法.大致可以將現(xiàn)有在線學(xué)習(xí)方法分為利用模型一階信息和二階信息的方法.利用一階信息的在線學(xué)習(xí)算法有感知機(jī)算法(perceptron learning algorithm, PLA)[7]、PA算法[5]、在線梯度下降算法(online gradient descent algorithm, OGD)[19]等.感知機(jī)算法只在當(dāng)前模型預(yù)測(cè)出現(xiàn)錯(cuò)誤的情況下才會(huì)更新，而PA算法只要當(dāng)模型產(chǎn)生的預(yù)測(cè)損失不為0(即使數(shù)據(jù)標(biāo)簽預(yù)測(cè)正確)，都會(huì)主動(dòng)更新當(dāng)前模型.其核心思想是尋找與當(dāng)前分類(lèi)模型最近鄰的約束，若當(dāng)前模型對(duì)新來(lái)數(shù)據(jù)預(yù)測(cè)沒(méi)有損失，模型不更新，否則，模型主動(dòng)更新，即投影到離現(xiàn)有分類(lèi)模型最近鄰的位置.因此，PA算法在大多數(shù)情形下都會(huì)顯著的優(yōu)于感知機(jī)算法.在線梯度下降算法在每次迭代時(shí)都沿當(dāng)前損失函數(shù)梯度下降的方向更新模型，然后將更新后的模型投影到可行域中.利用二階信息的在線算法有二階感知機(jī)算法[20]、NHERD[21]算法(normal herding method via Gaussian herding)、SCW(soft confidence weighted algorithm)算法[22]、IELLIP(online learning algorithms by improved Ellipsoid)算法[23]、AROW(adaptive regularization of weight vectors)算法[24]等.利用二階信息的算法有著更優(yōu)異的預(yù)測(cè)效果，但是其計(jì)算開(kāi)支與一階算法相比更大.

以上這些算法建立在數(shù)據(jù)特征空間固定的基礎(chǔ)之上，不能直接在動(dòng)態(tài)特征的場(chǎng)景下進(jìn)行應(yīng)用.為解決動(dòng)態(tài)特征場(chǎng)景下的在線學(xué)習(xí)問(wèn)題，極少部分研究者結(jié)合各種特征演化規(guī)律，提出了一些在線動(dòng)態(tài)特征學(xué)習(xí)算法.Zhang等人首先對(duì)數(shù)據(jù)數(shù)量與特征維度隨時(shí)間不斷增加的場(chǎng)景進(jìn)行了研究，提出了OLSF系列算法(online learning with streaming features)[14].Zhang等人將數(shù)量與特征維度都隨時(shí)間增加的數(shù)據(jù)稱(chēng)為梯形數(shù)據(jù)，當(dāng)新到達(dá)的數(shù)據(jù)攜帶了新的特征時(shí)，OLSF算法將數(shù)據(jù)特征分為歷史特征和新增特征2部分，通過(guò)改進(jìn)PA算法使得分類(lèi)器在面對(duì)2種特征時(shí)執(zhí)行不同的在線更新規(guī)則.針對(duì)訓(xùn)練集固定、特征以流到來(lái)的場(chǎng)景，Wu等人[25]提出了OSFS(online streaming feature selection)算法對(duì)數(shù)據(jù)進(jìn)行在線特征選擇.Hou等人[26]在OLSF的基礎(chǔ)上研究了特征有增有減的場(chǎng)景，提出FESL(feature evolvable streaming learning)算法，其假設(shè)數(shù)據(jù)的歷史特征是同時(shí)消失的，不具有繼承性.FESL通過(guò)在新增特征與歷史特征共存的階段學(xué)習(xí)特征之間的映射關(guān)系，從而在歷史特征消失后可以利用新增特征對(duì)歷史特征進(jìn)行恢復(fù)，并在2種特征上分別訓(xùn)練分類(lèi)器，最后利用集成學(xué)習(xí)的思想對(duì)2個(gè)預(yù)測(cè)結(jié)果進(jìn)行集成得到最后的分類(lèi)結(jié)果.在FESL算法的基礎(chǔ)上，后續(xù)發(fā)展了EDM(evolving discrepancy minimization)[27]和PUFE(prediction with unpredictable feature evolution)算法[28]，對(duì)FESL場(chǎng)景進(jìn)行了深入探索和擴(kuò)展.進(jìn)一步地，有研究者研究了數(shù)據(jù)流的特征可以任意新增或消失的情形.如He等人[29]提出了OLVF算法(online learning with varying feature space)，將當(dāng)前樣本的特征分為存留特征、共享特征和新特征3部分，將現(xiàn)有模型投影到共享的特征空間中進(jìn)行預(yù)測(cè)更新.Beyazit等人[30]提出了GLSC算法(generative learning with streaming capricious data)，在全特征空間上學(xué)習(xí)新特征與舊特征之間的映射關(guān)系.

2 面向特征繼承性增減的在線學(xué)習(xí)算法

本節(jié)首先詳細(xì)介紹繼承性增減的場(chǎng)景以及本文用到的符號(hào)和相關(guān)含義，然后對(duì)OFID算法進(jìn)行介紹，梳理算法的整體思路，提出相關(guān)策略并形成對(duì)應(yīng)的優(yōu)化問(wèn)題，然后對(duì)優(yōu)化問(wèn)題進(jìn)行求解，在最后給出算法的偽代碼.

2.1 問(wèn)題設(shè)定以及相關(guān)符號(hào)

本文需要完成特征繼承性增減場(chǎng)景下的在線二分類(lèi)任務(wù)，本節(jié)首先介紹該場(chǎng)景下數(shù)據(jù)特征的變化特點(diǎn)，后面列出用到的符號(hào)與概念，最后抽象為數(shù)學(xué)形式上的問(wèn)題.

本場(chǎng)景下數(shù)據(jù)的變化呈現(xiàn)出明顯的階段性趨勢(shì)，如圖1所示，以數(shù)據(jù)特征經(jīng)歷一輪完整的繼承性增減的時(shí)間為一個(gè)處理階段，例如階段1～T2-b2，不同階段數(shù)據(jù)的特征變化非常相似，在處理數(shù)據(jù)時(shí)可以按照階段進(jìn)行.每個(gè)階段大致可以分為3個(gè)部分，每個(gè)部分內(nèi)數(shù)據(jù)的特征保持穩(wěn)定，突變發(fā)生在第2，3部分，單階段內(nèi)特征變化規(guī)律為：

① 1～T1-b1

這段時(shí)間內(nèi)數(shù)據(jù)的特征空間與第1個(gè)樣本相同，此階段的數(shù)據(jù)具有特征S1與S2；

②T1-b1+1～T1

本階段的初始，t=T1-b1+1時(shí)，特征空間發(fā)生突變，數(shù)據(jù)的維度升高，此時(shí)數(shù)據(jù)攜帶特征S1，S2與S3，本時(shí)段也被稱(chēng)為過(guò)渡階段；

③T1+1～T1+T2-b2

在本階段，與上個(gè)階段相比，數(shù)據(jù)特征減少，特征S2，S3得到繼承，特征S1消失.

上述場(chǎng)景可以抽象為一個(gè)特征繼承性增減的在線二分類(lèi)問(wèn)題.在本文中用{xt,t=1,2,…,T1+T2-b2}表示序貫接收的樣本，其中xt∈dt，表示xt是一個(gè)dt維的行向量.wt是t-1輪迭代后得到的分類(lèi)器.在t=T1-b1+1時(shí)，新增特征出現(xiàn)，為了對(duì)歷史特征和新增特征加以區(qū)別，文中用表示原始特征組成的向量，表示新增特征組成的向量，原始特征是樣本xt在x1特征空間上的投影，新增特征是樣本xt的剩余部分，即其中分類(lèi)器w做同樣的劃分，用yt表示樣本xt的真實(shí)標(biāo)簽，表示分類(lèi)器的預(yù)測(cè)結(jié)果.

Table 1 Notations and Descriptions表1 符號(hào)及其含義

2.2 OFID算法

觀察特征的演化規(guī)律可以發(fā)現(xiàn)算法有2個(gè)最主要的問(wèn)題需要解決，主要問(wèn)題1：在T1-b1+1～T1階段，新的特征S3出現(xiàn)，加入訓(xùn)練會(huì)對(duì)第1階段訓(xùn)練得到的分類(lèi)器產(chǎn)生影響；T1-b1+1～T1階段維持時(shí)間較短，數(shù)據(jù)數(shù)少，如何設(shè)計(jì)更新策略、在初期攜帶新特征的數(shù)據(jù)不足的情況下進(jìn)行較為準(zhǔn)確的訓(xùn)練是一個(gè)問(wèn)題.主要問(wèn)題2：在T1+1～T1+T2-b2階段，特征S1消失，只利用具有相同特征空間的數(shù)據(jù)進(jìn)行模型訓(xùn)練，對(duì)應(yīng)缺失維度的信息就會(huì)丟失，造成信息的浪費(fèi)，降低預(yù)測(cè)準(zhǔn)確率.既要盡可能的減少信息的損失，保證預(yù)測(cè)準(zhǔn)確率，又要適應(yīng)周期內(nèi)特征空間的增減變化，這是算法需要解決的技術(shù)重點(diǎn)，針對(duì)特征繼承性增減的在線分類(lèi)場(chǎng)景，本文提出面向特征繼承性增減的在線分類(lèi)算法OFID及其2種變體.對(duì)于問(wèn)題1，算法的策略是在第2階段更新時(shí)引入新分類(lèi)器對(duì)新增特征進(jìn)行學(xué)習(xí)，但盡量維持上個(gè)階段分類(lèi)器的權(quán)重.歷史模型在原始特征的多輪迭代上得到了充分訓(xùn)練，具有較高的置信度，因此采用維持原有分類(lèi)器的更新策略，進(jìn)行上述處理，模型可能會(huì)增加對(duì)舊特征的依賴，對(duì)于該問(wèn)題，OFID算法在下個(gè)處理過(guò)程中，放棄了對(duì)于舊特征的恢復(fù)，只對(duì)新分類(lèi)器進(jìn)行訓(xùn)練，在一定程度上避免了模型對(duì)舊特征的依賴，達(dá)到了充分?jǐn)M合新特征的目的；對(duì)于問(wèn)題2，本文采用FD算法對(duì)矩陣進(jìn)行補(bǔ)全.補(bǔ)全后的數(shù)據(jù)矩陣可以采用已有的成熟技術(shù)進(jìn)行在線分類(lèi).

本文在第1部分采取PA算法進(jìn)行模型更新，因?yàn)镻A算法具有十分顯著的優(yōu)點(diǎn)：1)PA算法是在線學(xué)習(xí)任務(wù)中應(yīng)用十分廣泛的算法，具有良好的收斂速度；2)PA算法在保證良好學(xué)習(xí)性能的前提下，具有較快的運(yùn)行速率；3)利用PA算法可以使OFID算法具有良好的理論保證.因此本文使用PA算法進(jìn)行模型更新.

本場(chǎng)景下數(shù)據(jù)呈現(xiàn)明顯的特征增減規(guī)律，在1～T1-b1時(shí)間段內(nèi)，特征空間保持不變，本階段內(nèi)第t輪迭代時(shí)，PA算法滿足的優(yōu)化表達(dá)式為

(1)

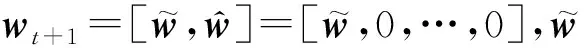
(2)

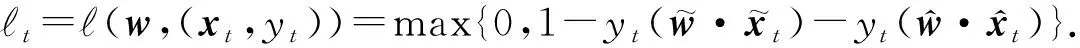
以上處理解決了特征增加時(shí)分類(lèi)器對(duì)新增特征的適應(yīng)問(wèn)題。然而，在T1+1～T1+T2-b2階段，特征S1消失，數(shù)據(jù)矩陣出現(xiàn)了缺失.為了繼續(xù)使用和訓(xùn)練原有分類(lèi)器，算法選擇利用過(guò)渡階段的完整數(shù)據(jù)進(jìn)行矩陣補(bǔ)全.

在傳統(tǒng)特征變化的研究中[26,31]，通常采用新特征來(lái)補(bǔ)全舊特征，達(dá)到挖掘新舊特征之間的關(guān)系的目的.然而，本文研究的特征繼承性增減的實(shí)際應(yīng)用場(chǎng)景中，下一時(shí)刻數(shù)據(jù)哪些特征會(huì)發(fā)生缺失無(wú)法事先確定，難以通過(guò)學(xué)習(xí)新舊特征之間的關(guān)系來(lái)對(duì)消失的舊特征進(jìn)行補(bǔ)全.因此，本論文采取FD算法進(jìn)行補(bǔ)全，F(xiàn)D算法的基本思路是尋找出現(xiàn)頻率高的向量作為一組基來(lái)補(bǔ)全數(shù)據(jù)矩陣，將單個(gè)的數(shù)據(jù)樣本作為整體來(lái)處理，可以很好地解決新舊特征不確定的問(wèn)題，對(duì)缺失特征進(jìn)行有效準(zhǔn)確的補(bǔ)全.

FD算法不考察特征之間的關(guān)系，其補(bǔ)全流程是建立一個(gè)r行的矩陣，最后一行設(shè)置為零向量，每一個(gè)樣本被接收后作為一個(gè)行向量替代掉矩陣中的零向量，然后對(duì)矩陣做SVD分解，將最小的奇異值剔除，繼續(xù)按照以上步驟操作，遍歷所有數(shù)據(jù).最終返回一個(gè)草圖矩陣.

T1-b1+1～T1階段接收到的樣本組成矩陣N，對(duì)矩陣N使用FD算法繪制秩為r的矩陣草圖B，記B的行向量為vi,i∈{1,2,…,r}，構(gòu)成一個(gè)向量組，B的行空間記為V，利用V對(duì)T1+1～T1+T2-b2階段的缺失部分進(jìn)行補(bǔ)全.

在T1+1～T1+T2-b2階段的第t輪迭代，接收到樣本xt，在V中尋找一個(gè)向量zt，記zt∈V，該向量滿足:

(3)

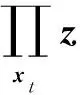
(4)

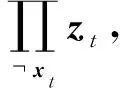
(5)

(6)

第2個(gè)是ξ的平方形式：

(7)

(8)

以此形成2種變體算法OFID -Ⅰ與OFID -Ⅱ，它們是OFID算法的軟間隔形式.

傳統(tǒng)的在線學(xué)習(xí)算法每次接收一個(gè)數(shù)據(jù)就進(jìn)行模型的更新，因此具有運(yùn)行速度快、存儲(chǔ)空間要求小等優(yōu)點(diǎn)，而本文提出的OFID系列算法每次接收一個(gè)數(shù)據(jù)就進(jìn)行分類(lèi)器的更新，具有傳統(tǒng)在線學(xué)習(xí)算法的優(yōu)點(diǎn)，屬于典型的在線學(xué)習(xí)算法.但由于本文的核心研究?jī)?nèi)容是特征繼承性增減這一特殊場(chǎng)景，作者在傳統(tǒng)的在線學(xué)習(xí)算法上做出了改進(jìn)，提高了算法對(duì)特征繼承性增減變化的適應(yīng)能力，增強(qiáng)了算法在該場(chǎng)景下的分類(lèi)能力.

2.3 優(yōu)化問(wèn)題求解

(9)

其中τ是拉格朗日乘數(shù)，將w的表達(dá)式代入L(w,τ)，進(jìn)一步有:

(10)

式(10)對(duì)τ求導(dǎo)，令其等于0，得到wt+1的閉式解：

(11)

優(yōu)化問(wèn)題式(2)的求解與問(wèn)題式(1)的求解類(lèi)似，使用拉格朗日乘子法，有:

(12)

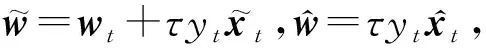
(13)

式(13)對(duì)τ求導(dǎo)，令其等于0，得到wt+1的閉式解：

(14)

繼續(xù)使用拉格朗日乘子法對(duì)優(yōu)化問(wèn)題式(5)～(8)進(jìn)行求解，得到2個(gè)變體算法統(tǒng)一的更新方式，

(15)

其中，

(16)

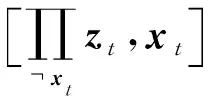
綜合以上求解過(guò)程，3種算法具有統(tǒng)一的更新形式：

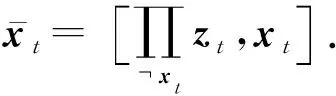
OFID算法及其他2種變體算法的偽代碼如下所示：

算法1.OFID算法及其變體.

輸入：參數(shù)C>0;

輸出：1～T1+T2-b2階段內(nèi)預(yù)測(cè)正確的樣本數(shù)量、草圖矩陣B.

初始化：w1=(0,…,0)∈d1;

fort=1,2,…,T1do

① 接收樣本xt;

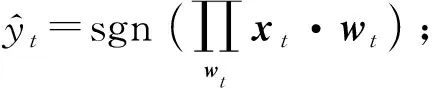
yt(w·xt)}，wt與xt維度相同時(shí)；

wt與xt維度不同時(shí).

④ 接收標(biāo)簽yt;

⑤ 計(jì)算步長(zhǎng)τt;

⑥ 利用算法2訓(xùn)練草圖矩陣B;

⑦ 更新分類(lèi)器：

end

fort=T1+1,…,T1+T2-b2-1 do

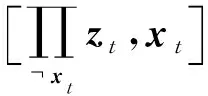
⑨ 重復(fù)步驟②③④⑤⑦

end

算法1中采用了Frequent-Directions學(xué)習(xí)草圖矩陣，其算法偽代碼為：

算法2.Frequent-Directions.

輸出：草圖矩陣B;

初始化：B=0r×dT1.

fort=T1-b1+1,…,T1do

①Br←xt;

② [U,Σ,V]←SVD(B);

③N←ΣVT;

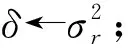
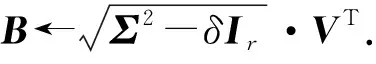
end

3 算法分析

本節(jié)對(duì)OFID系列算法的損失進(jìn)行討論與證明，在理論上保證算法的有效性和可靠性.本節(jié)用到了3個(gè)引理、3個(gè)定理.引理1用于說(shuō)明FD算法在條件滿足的情況下可以精確地對(duì)矩陣進(jìn)行補(bǔ)全；引理2，3與定理1用于說(shuō)明數(shù)據(jù)集線性可分情況下OFID算法Hinge損失平方和有上界；定理2用于說(shuō)明算法OFID -Ⅰ犯錯(cuò)總數(shù)有上界；定理3用于說(shuō)明算法OFID -Ⅱ的Hinge損失平方和有上界.

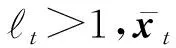
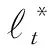
引理1.在算法2中，對(duì)矩陣B做SVD分解，B=UΣVT，令r∈{min(T1-b,d1)}，即r是草圖矩陣B的秩，并且有U=(u1,u2,…,ur)∈(T1-b)×r，V=(v1,v2,…,vr)∈(T1-b)×r，記和是矩陣B的前r個(gè)左右奇異向量.定義:

若滿足s≥7μ(r)rln(rb1/δ)，s為消失特征的維數(shù)，則在至少1-δ的概率下算法可以將矩陣精確地進(jìn)行恢復(fù).

證明.引理1的詳細(xì)證明可參考文獻(xiàn)[18].

引理2[14].記(xt,yt)，t=1,2,…,T為序貫接收的流式數(shù)據(jù)，其中xt∈dt，yt∈{-1,+1}，數(shù)據(jù)的維數(shù)滿足dt-1≤dt，步長(zhǎng)損失t采用Hinge損失，則對(duì)任意向量u∈dT，有:

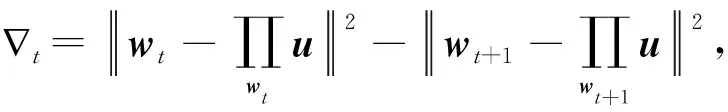
(17)

即:

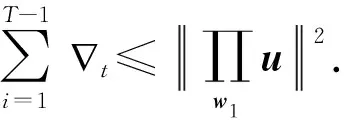
下面對(duì)單項(xiàng)的?t進(jìn)行估計(jì).在t=0時(shí)，τt=0，有又dwt≤dwt+1，則有:

(18)

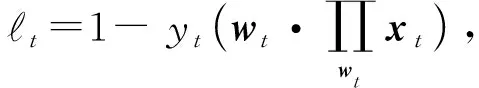
(19)

式(19)兩邊對(duì)t累加，可得:

(20)

證畢.

引理3[14].記(xt,yt)，t=1,2,…,T為序貫接收的流式數(shù)據(jù)，其中xt∈dt，yt∈{-1,+1}，dt-1≤dt并且對(duì)所有t均成立；假設(shè)存在分類(lèi)器u∈dT，在任意一次迭代中滿足則有：

(21)

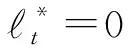
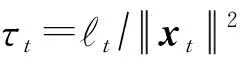
(22)

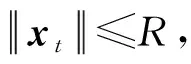
證畢.

定理1.記(xt,yt)，t=1,2,…,T1+T2-b2為序貫接收的流式數(shù)據(jù)，其中xt∈dt，yt∈{-1,+1}，補(bǔ)全后的樣本滿足對(duì)所有t均成立；分類(lèi)器滿足對(duì)所有t均成立；假設(shè)存在分類(lèi)器u∈dT，對(duì)補(bǔ)全后的矩陣，對(duì)任意的t滿足令R=max{R1,R2}，則有:

證明.令：

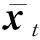
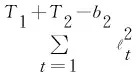
?t對(duì)t進(jìn)行累加，得到:

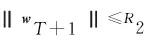
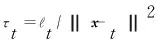
證畢.

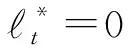
定理2.記(xt,yt),t=1,2,…,T1+T2-b2為序貫接收的流式數(shù)據(jù)，其中xt∈dt，yt∈{-1,+1}，補(bǔ)全后的樣本滿足對(duì)所有t均成立，則對(duì)于任意向量u∈dT1，算法OFID -Ⅰ犯錯(cuò)次數(shù)的一個(gè)上界為

證明.令

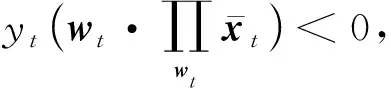
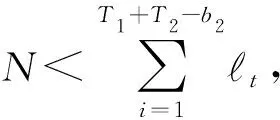
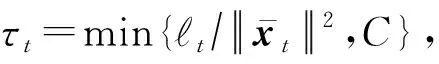
代入后得到式(21)中，得到:

整理后得到:

證畢.

定理2說(shuō)明了算法OFID -Ⅰ在恢復(fù)出的樣本有界時(shí)，犯錯(cuò)總數(shù)存在上界.

定理3.記(xt,yt),t=1,2,…,T1+T2-b2為序貫接收的流式數(shù)據(jù)，其中xt∈dt，yt∈{-1,+1}，補(bǔ)全后的樣本滿足對(duì)所有t均成立，則對(duì)于任意向量u，u∈dT1，有:

證明.通過(guò)引理2已知:

(23)

(24)

將τt的定義代入，有:

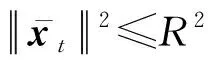
通過(guò)定理3，在理論上驗(yàn)證了OFID -Ⅱ算法的Hinge損失平方和有上界.

證畢.

4 實(shí) 驗(yàn)

本節(jié)通過(guò)數(shù)值仿真實(shí)驗(yàn)來(lái)驗(yàn)證OFID算法及其2種變體的表現(xiàn).首先介紹實(shí)驗(yàn)設(shè)置及數(shù)據(jù)集.

本節(jié)共設(shè)置4組實(shí)驗(yàn)，組1實(shí)驗(yàn)為主試驗(yàn)，進(jìn)行OFID系列算法與FESL-c，F(xiàn)ESL-s，PUFE算法的對(duì)比，使用預(yù)測(cè)準(zhǔn)確率作為指標(biāo)，觀察OFID系列算法在具體數(shù)據(jù)集上的表現(xiàn)，驗(yàn)證OFID算法的有效性和可靠性；組2實(shí)驗(yàn)為參數(shù)實(shí)驗(yàn)，以預(yù)測(cè)錯(cuò)誤率為指標(biāo)，考察2種變體算法的參數(shù)敏感性以及添加松弛變量的效果；組3實(shí)驗(yàn)為算法時(shí)間復(fù)雜的實(shí)驗(yàn)，指標(biāo)為時(shí)間，用來(lái)考察算法的時(shí)間復(fù)雜度.組4實(shí)驗(yàn)為輔助實(shí)驗(yàn)，指標(biāo)為算法的預(yù)測(cè)正確率，在3個(gè)不同的迭代階段分別記錄并進(jìn)行對(duì)比，驗(yàn)證OFID算法在不同迭代階段的有效性.

實(shí)驗(yàn)數(shù)據(jù)要求具有動(dòng)態(tài)的特征空間，為滿足這一要求，對(duì)特征空間進(jìn)行了劃分，劃分的樣式如圖1所示，每個(gè)數(shù)據(jù)集的特征隨機(jī)進(jìn)行排序，近似均分為3部分；在場(chǎng)景設(shè)置中T1-b1+1～T1階段維持時(shí)間較短，在劃分?jǐn)?shù)據(jù)集時(shí)遵循了這一設(shè)定，過(guò)渡階段的數(shù)據(jù)量占比設(shè)置為1/10，階段1的數(shù)據(jù)比例與缺失數(shù)據(jù)的比例等同，我們按照以上規(guī)則對(duì)數(shù)據(jù)集進(jìn)行劃分.

每次實(shí)驗(yàn)每個(gè)數(shù)據(jù)集重復(fù)20次，每次重復(fù)隨機(jī)打亂數(shù)據(jù)的順序，并使用20次結(jié)果的平均值作為指標(biāo)的最終值.參數(shù)實(shí)驗(yàn)中，總共進(jìn)行9次調(diào)參，參數(shù)C的選擇范圍為10-4～104，參數(shù)C的每次變化倍率為10.

本文在公開(kāi)數(shù)據(jù)集上進(jìn)行實(shí)驗(yàn)，包括Cancer，air，WDBC，warpPIE，WBC，Haberman，Wine，Thyroid，Seeds共9個(gè)數(shù)據(jù)集，這些數(shù)據(jù)集分布在多個(gè)領(lǐng)域.數(shù)據(jù)集的情況如表2所示：

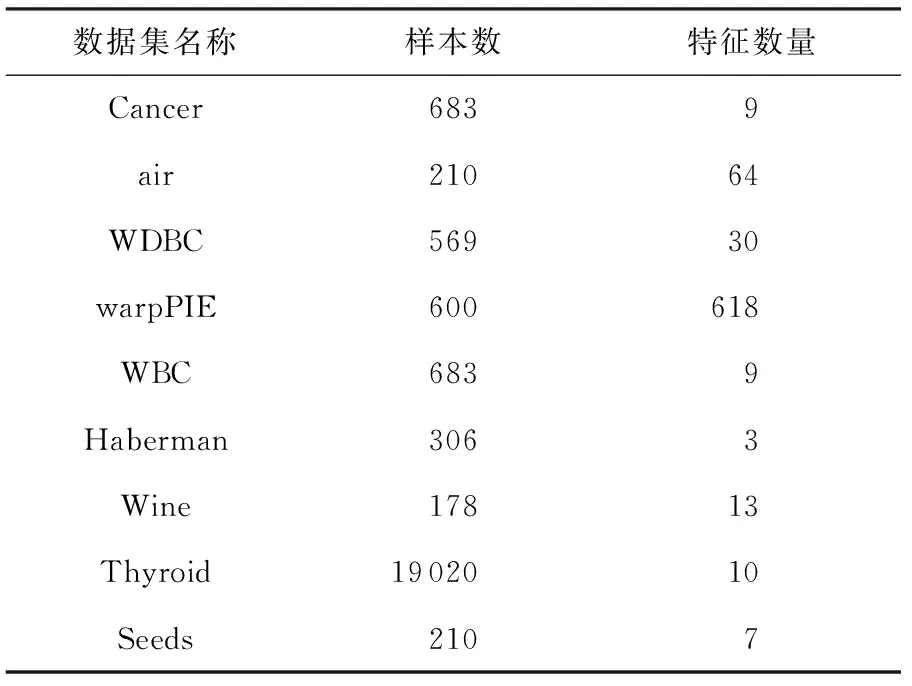
Table 2 The Datasets Used in the Experiments表2 實(shí)驗(yàn)中用到的數(shù)據(jù)集

4.1 OFID系列算法與FESL,PUFE算法的對(duì)比實(shí)驗(yàn)

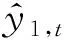
表3展示了6種算法在不同數(shù)據(jù)集上的最終預(yù)測(cè)準(zhǔn)確率.在大多數(shù)數(shù)據(jù)集上，OFID系列算法與其他算法相比有著較高的預(yù)測(cè)準(zhǔn)確率，說(shuō)明OFID系列算法較好地適應(yīng)了數(shù)據(jù)特征的動(dòng)態(tài)變化，具有現(xiàn)實(shí)應(yīng)用的價(jià)值.但是一個(gè)學(xué)習(xí)過(guò)程中，3個(gè)階段的數(shù)據(jù)的特征有較大的差異，因此最終的預(yù)測(cè)準(zhǔn)確率并不足以概括在整個(gè)學(xué)習(xí)過(guò)程各個(gè)算法的表現(xiàn).為更加直觀地觀察算法在各個(gè)階段的表現(xiàn)，本文選取預(yù)測(cè)錯(cuò)誤率作為指標(biāo)，觀察6種算法在學(xué)習(xí)過(guò)程中預(yù)測(cè)錯(cuò)誤率的動(dòng)態(tài)變化，實(shí)驗(yàn)結(jié)果如圖2所示.

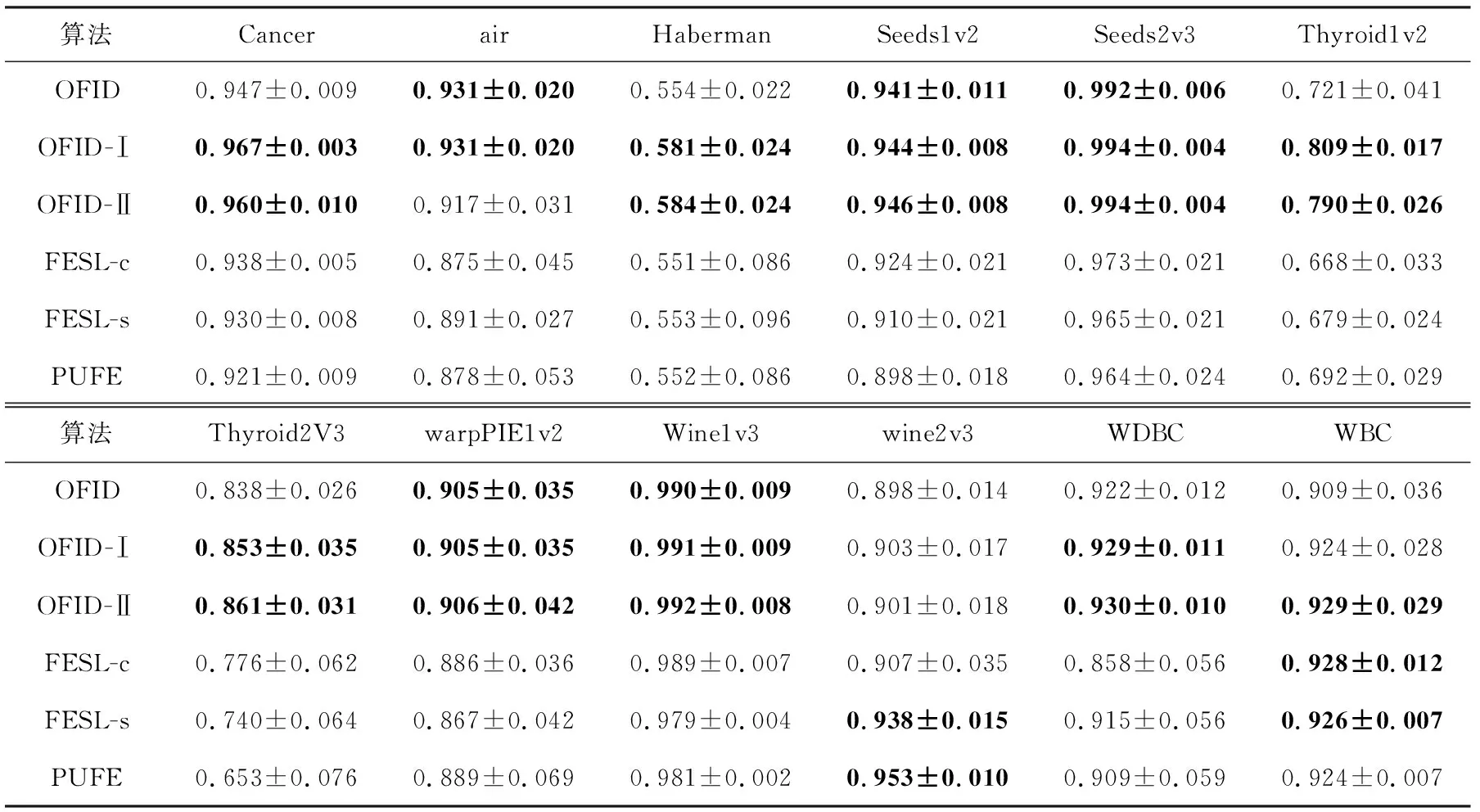
Table 3 Prediction Accuracy of Six Algorithms on Different Datasets表3 6種算法在不同數(shù)據(jù)集上的預(yù)測(cè)準(zhǔn)確率

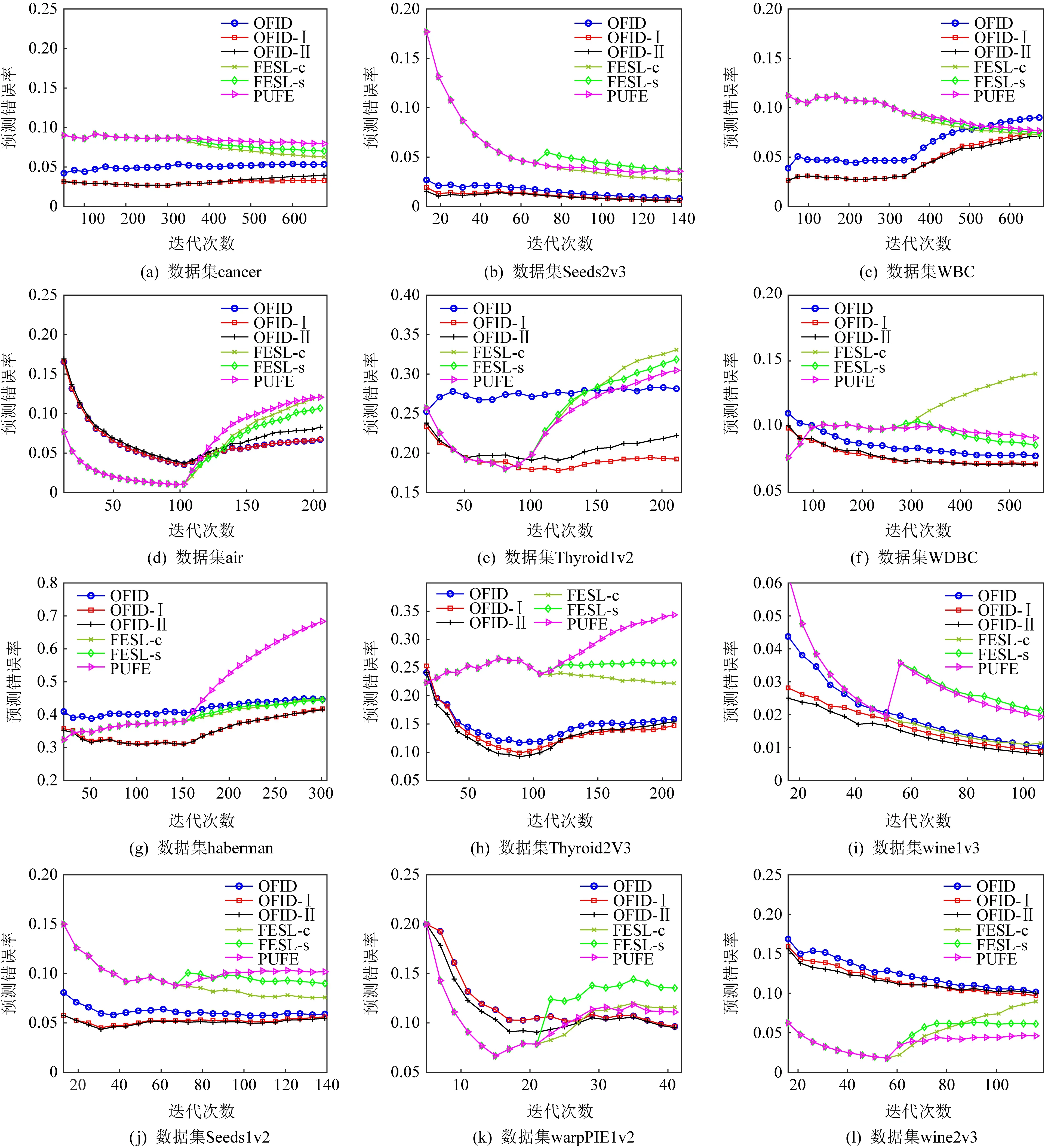
Fig. 2 Prediction wrong rates of six algorithms on different datasets圖2 6種算法在不同數(shù)據(jù)集上的預(yù)測(cè)錯(cuò)誤率

圖2是6種算法在數(shù)據(jù)集上預(yù)測(cè)錯(cuò)誤率隨時(shí)間的變化情況，橫坐標(biāo)是迭代次數(shù)，縱坐標(biāo)是平均預(yù)測(cè)錯(cuò)誤率.OFID -Ⅰ，OFID -Ⅱ在大多數(shù)數(shù)據(jù)集上表現(xiàn)優(yōu)于算法OFID.說(shuō)明軟間隔形式取得了應(yīng)有的設(shè)計(jì)效果，降低了對(duì)噪聲的敏感程度，提高了算法性能.

在大多數(shù)數(shù)據(jù)集上，OFID -Ⅰ(紅色)、OFID -Ⅱ(黑色)算法表現(xiàn)最好，算法OFID(藍(lán)色)次之，表現(xiàn)優(yōu)于其他3種算法，說(shuō)明OFID系列算法具有實(shí)際應(yīng)用的價(jià)值，該實(shí)驗(yàn)驗(yàn)證了算法的有效性.

算法FESL，PUFE在數(shù)據(jù)集Wine上表現(xiàn)較OFID更好.在其余數(shù)據(jù)集上，OFID系列算法表現(xiàn)最優(yōu).對(duì)于上述實(shí)驗(yàn)結(jié)果進(jìn)行觀察，會(huì)發(fā)現(xiàn)1～T1-b1階段的預(yù)測(cè)正確率對(duì)算法FESL，PUFE的整體表現(xiàn)有重要的影響，F(xiàn)ESL，PUFE的整體表現(xiàn)優(yōu)于OFID系列算法時(shí)在1～T1-b1階段的預(yù)測(cè)優(yōu)于OFID系列算法.

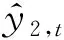
4.2 參數(shù)實(shí)驗(yàn)

在本節(jié)進(jìn)行參數(shù)實(shí)驗(yàn)，評(píng)價(jià)指標(biāo)為20次實(shí)驗(yàn)的平均預(yù)測(cè)正確率，觀察參數(shù)變化對(duì)實(shí)驗(yàn)結(jié)果的影響，考察OFID系列算法對(duì)參數(shù)C的敏感程度，圖3為參數(shù)實(shí)驗(yàn)的具體結(jié)果，橫坐標(biāo)為參數(shù)C的數(shù)值，參數(shù)C的范圍為10-4～104，縱坐標(biāo)為平均預(yù)測(cè)正確率.OFID算法無(wú)參數(shù)，不受參數(shù)變化影響，形成實(shí)驗(yàn)的固定參照；觀察圖3，隨著參數(shù)C的變動(dòng)，可以發(fā)現(xiàn)OFID -Ⅰ，OFID -Ⅱ的預(yù)測(cè)正確率隨之產(chǎn)生了一定程度的波動(dòng).參數(shù)過(guò)小時(shí)，OFID算法與OFID -Ⅰ，OFID -Ⅱ算法之間的預(yù)測(cè)正確率存在差距，但隨著參數(shù)C逐漸增大，3種算法準(zhǔn)確率之間的差距先增大后減小，最后趨同.

從優(yōu)化問(wèn)題的結(jié)構(gòu)來(lái)分析出現(xiàn)圖中變化趨勢(shì)的原因，參數(shù)C調(diào)節(jié)的是優(yōu)化表達(dá)式中松弛變量與分類(lèi)器變化2部分的比率，當(dāng)C增大時(shí)，要最小化優(yōu)化問(wèn)題式(5)～(8)，代表著松弛條件收緊，對(duì)應(yīng)的ξ值變小，損失降低，對(duì)數(shù)據(jù)的敏感性提高，隨著參數(shù)C增大，2種變體算法逐漸向沒(méi)有松弛變量的OFID算法靠攏，分析結(jié)果剛好與圖3的實(shí)驗(yàn)結(jié)果對(duì)應(yīng).

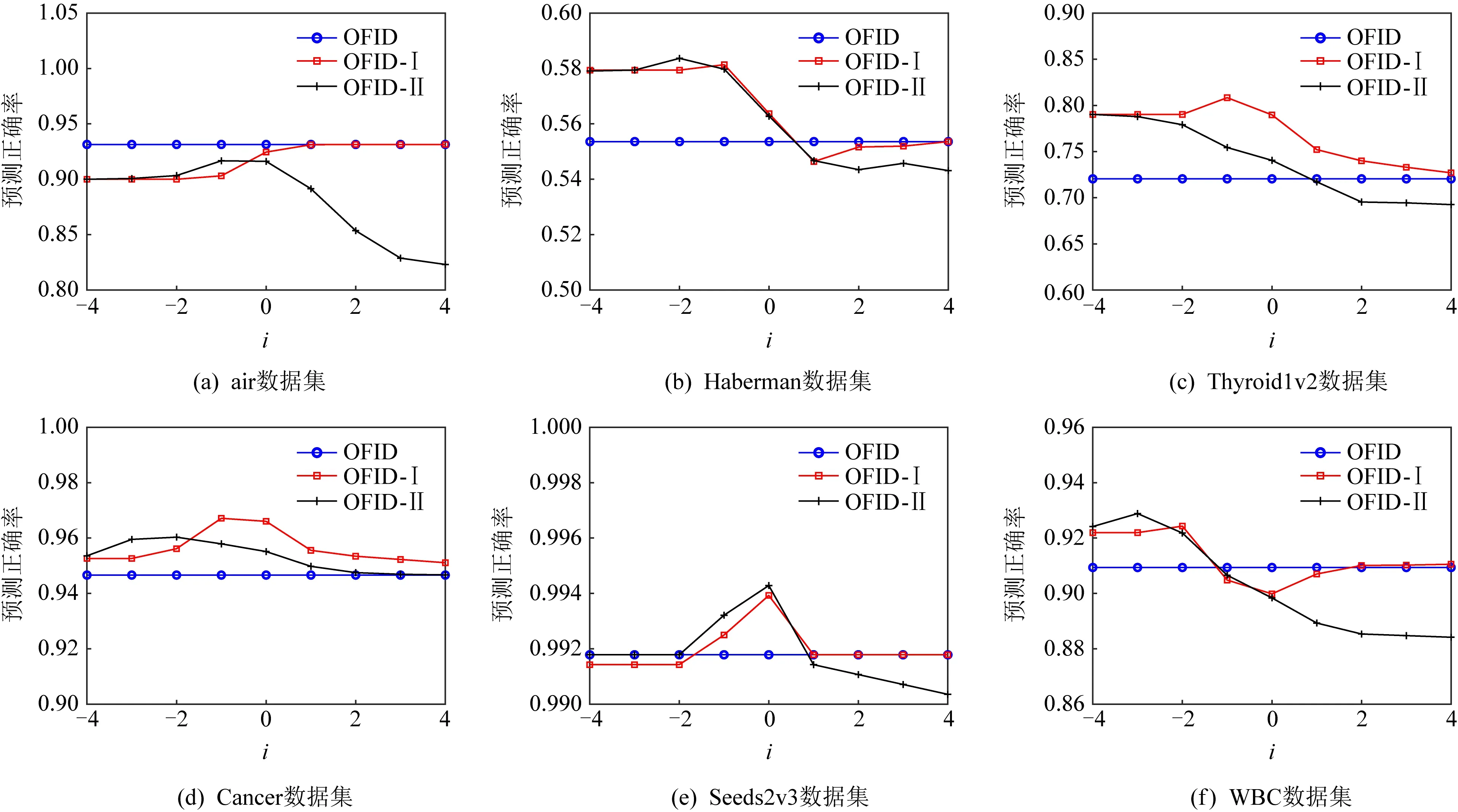
Fig. 3 The average rates of right predictions with respect to C=10i圖3 C=10i對(duì)平均預(yù)測(cè)正確率的影響

4.3 算法的時(shí)間復(fù)雜的實(shí)驗(yàn)

本節(jié)實(shí)驗(yàn)中，評(píng)價(jià)算法計(jì)算復(fù)雜度的指標(biāo)為算法得到預(yù)測(cè)結(jié)果的運(yùn)行時(shí)間.6種算法在不同數(shù)據(jù)集上的運(yùn)行時(shí)間如表4所示.

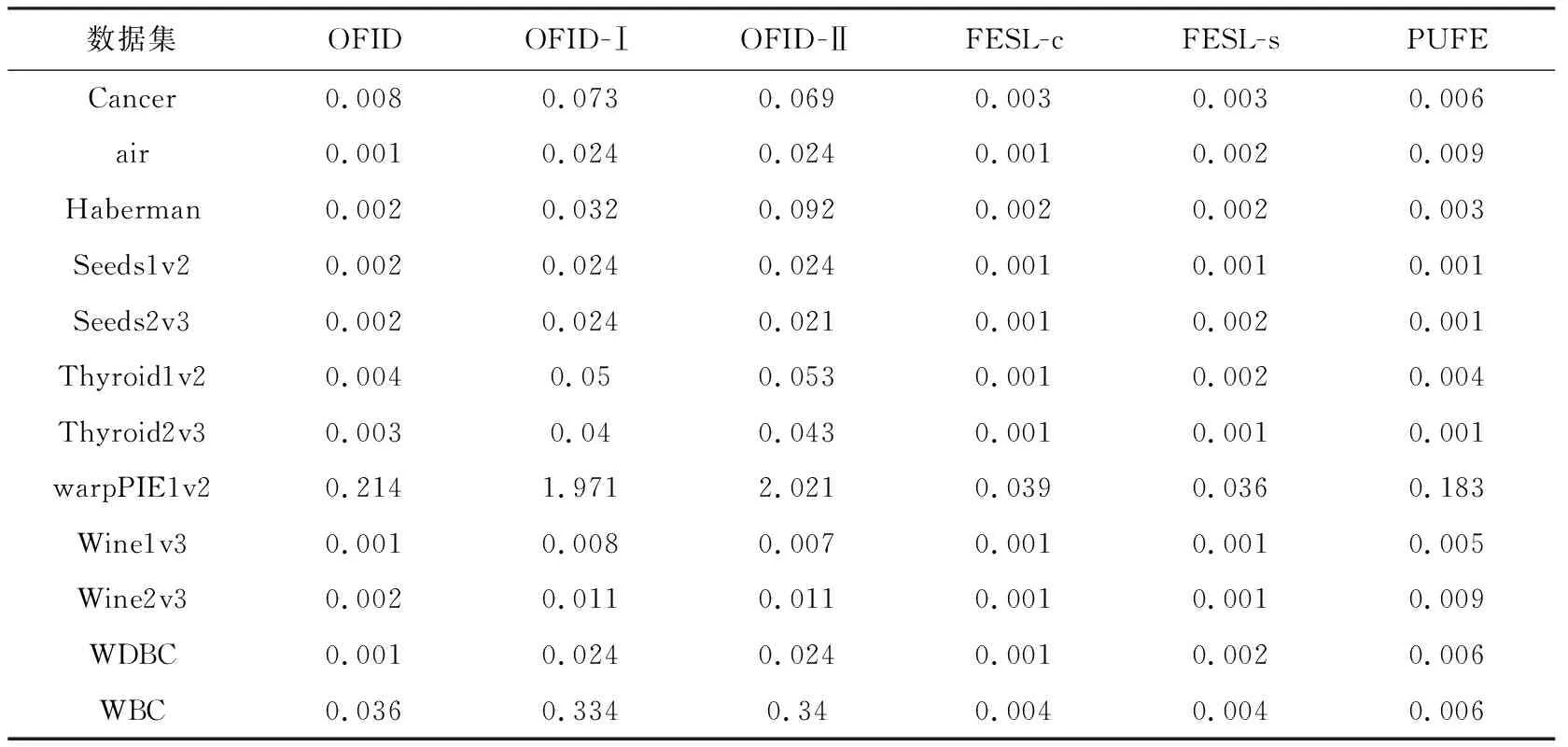
Table 4 Running Time of Different Algorithms on Different Datasets表4 不同算法在不同數(shù)據(jù)集的運(yùn)行時(shí)間 s

6種算法的更新表達(dá)式在形式上并無(wú)本質(zhì)上的不同，均為線性迭代算法，區(qū)別只在于每一步迭代中使用的系數(shù)，這并不會(huì)有時(shí)間消耗上的顯著差異，因此，復(fù)雜度存在差異的主要原因在于矩陣補(bǔ)全的方式.OFID系列算法與PUFE算法均使用FD算法進(jìn)行補(bǔ)全，F(xiàn)ESL算法在過(guò)渡階段訓(xùn)練一個(gè)線性映射進(jìn)行補(bǔ)全，這涉及到了矩陣的求逆運(yùn)算.這也是時(shí)間消耗的主要部分.

表4中OFID -Ⅰ與OFID -Ⅱ算法的運(yùn)行時(shí)間明顯高于其他算法，這是因?yàn)檫@2種算法需要進(jìn)行參數(shù)的調(diào)節(jié)，每得到一個(gè)調(diào)參后的預(yù)測(cè)結(jié)果，算法需要運(yùn)算9次，平均得到一個(gè)結(jié)果的時(shí)間與其他算法相當(dāng)；OFID算法與FESL算法、PUFE算法在時(shí)間消耗上相當(dāng)，具有相同的計(jì)算復(fù)雜度.

4.4 分階段預(yù)測(cè)實(shí)驗(yàn)

本節(jié)實(shí)驗(yàn)中選取4個(gè)數(shù)據(jù)集，觀測(cè)指標(biāo)為OFID系列算法與其他3種對(duì)比算法在3個(gè)不同階段的平均預(yù)測(cè)準(zhǔn)確率，預(yù)測(cè)結(jié)果取階段結(jié)束時(shí)算法的平均預(yù)測(cè)準(zhǔn)確率，具體的實(shí)驗(yàn)結(jié)果如圖4所示.觀察實(shí)驗(yàn)結(jié)果，可以發(fā)現(xiàn)OFID系列算法在迭代的3個(gè)階段里均有優(yōu)異的表現(xiàn)，這組輔助實(shí)驗(yàn)充分說(shuō)明了OFID系列算法在不同迭代階段均具有良好的分類(lèi)性能.

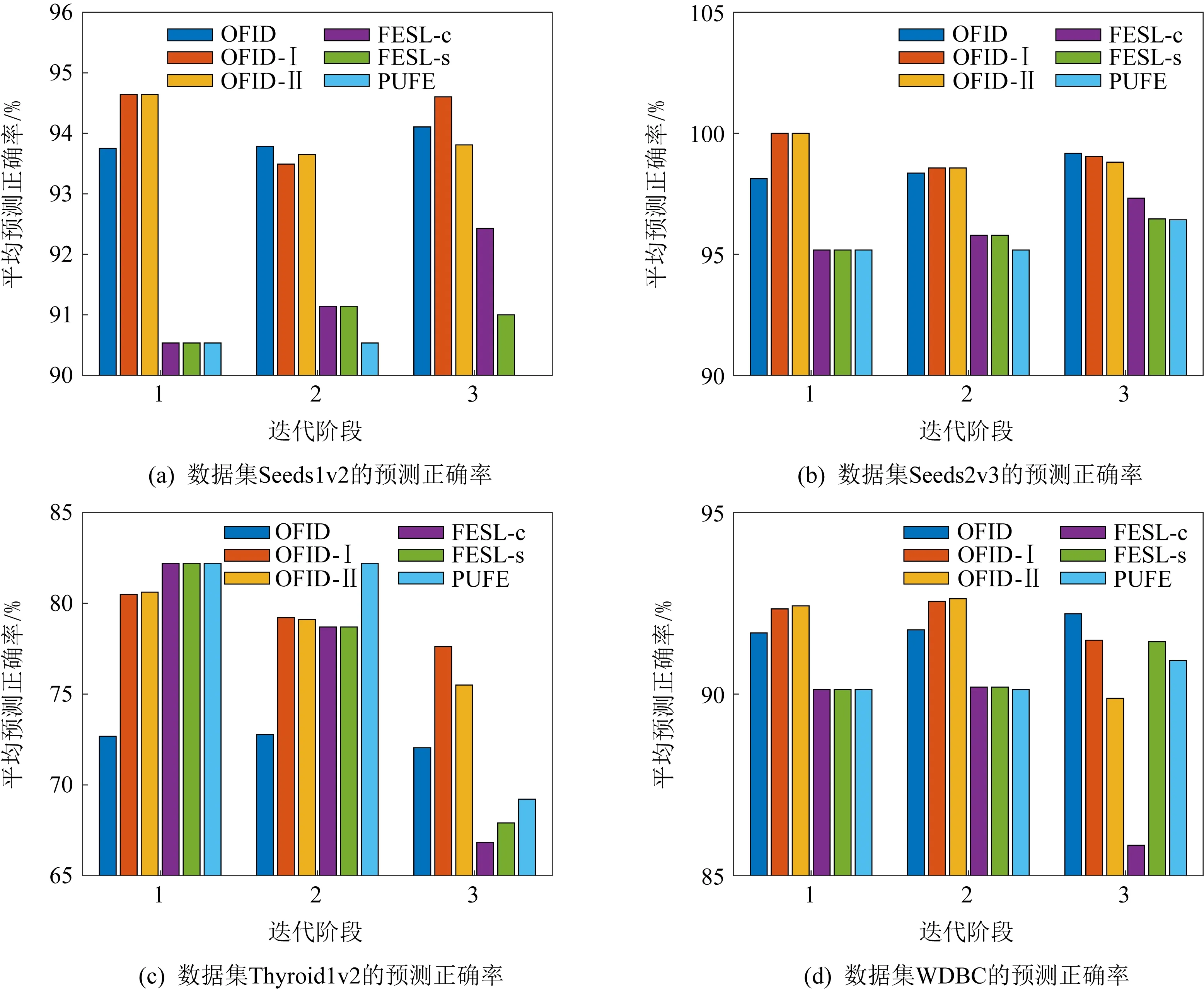
Fig. 4 The average prediction accuracy of the algorithm in three periods圖4 3個(gè)迭代階段中算法的平均預(yù)測(cè)準(zhǔn)確率

5 總結(jié)與展望

為解決數(shù)據(jù)流特征繼承性增減這一新的實(shí)際問(wèn)題，本文提出了一種面向特征繼承性增減的在線學(xué)習(xí)算法OFID及其2種變體OFID -Ⅰ與OFID -Ⅱ.當(dāng)新特征出現(xiàn)時(shí)，通過(guò)結(jié)合在線PA算法與結(jié)構(gòu)風(fēng)險(xiǎn)最小化原則分別更新原始特征與新增特征上的分類(lèi)器；當(dāng)原始特征消失時(shí)，對(duì)數(shù)據(jù)流使用Frequent-Directions算法對(duì)數(shù)據(jù)矩陣進(jìn)行補(bǔ)全，使得原始分類(lèi)器得以繼續(xù)更新迭代.理論分析和實(shí)驗(yàn)結(jié)果分析都驗(yàn)證了本文所提算法的有效性.

本文的對(duì)比方法中，有一些優(yōu)秀的思想可以進(jìn)行借鑒，例如對(duì)新舊分類(lèi)器分別進(jìn)行預(yù)測(cè)更新，互不干擾，預(yù)測(cè)標(biāo)簽來(lái)自新舊分類(lèi)器的預(yù)測(cè)結(jié)果進(jìn)行加權(quán)，這樣不僅避免了分類(lèi)器對(duì)舊特征的過(guò)渡依賴，并且可以充分利用恢復(fù)出的信息，有著較高的研究?jī)r(jià)值，這將是未來(lái)工作中我們努力的一個(gè)方向.

本文所提的算法主要是針對(duì)線性場(chǎng)景下的分類(lèi)問(wèn)題，因此，將本文算法擴(kuò)展到非線性場(chǎng)景下是我們未來(lái)非常重要的一項(xiàng)工作.同時(shí)，如何挖掘特征繼承性增減數(shù)據(jù)流的更多信息，例如二階信息、數(shù)據(jù)分布信息，以及如何對(duì)特征繼承性增減數(shù)據(jù)流進(jìn)行在線聚類(lèi)等也是值得關(guān)注的方向.因此，在未來(lái)的工作中我們將對(duì)上述內(nèi)容開(kāi)展更加深入的研究.