反應工程方法在鋰電池真空干燥模擬上的應用

楊興富，陳文，肖杰，陳曉東

（1 寧德新能源科技有限公司，福建 寧德 352100； 2 蘇州大學材料與化學化工學部，化工與環境工程學院，江蘇 蘇州 215123）

引 言

目前鋰離子電池無論是消費類電池還是汽車動力電池，與人們的生活息息相關，其電性能、安全性能是否達到要求，直接決定了它能否被市場接受。而鋰電池生產中，在注入電解液之前的真空干燥情況，決定了電芯極片內部的含水率，對于鋰電池一般要求水分含量低于150 mg/kg[1]。干燥程度不足將導致放電性能下降、跳水、電芯產氣等問題[1-2]，而過度干燥則會延長生產時間，降低生產效率。因此關于電芯真空干燥過程的仿真模擬，對電芯生產工藝改善、品質監控等方面有極高的應用價值。

目前文獻[3-7]報道較多的干燥模型，是基于極片層級的純擴散干燥模型。此類模型進行過多的簡化假設，例如：認為環境水分濃度等于真空度、不考慮極片內部多孔材料結構特性、假設蒸發只發生于極片表面等。此類模型基于實驗數據對標仿真，可以獲得一套模型參數，但當材料孔隙率、顆粒尺寸、材料體系、電芯尺寸等發生變化時，模型參數難以通用，阻礙了仿真預測的推廣應用。Murru 等[8]研究了在靜態條件下以正丙醇為溶劑的潮濕粉末的干燥過程，考慮了被干燥材料的多孔特性，加入基于殘余飽和度的蒸發速率方程，并且考慮了溶劑的平衡蒸氣壓，很好地模擬了粉末的干燥過程。Hou等[9]基于Murru 等[8]的方法拓展應用到獼猴桃切片的紅外真空干燥中，并加入固體收縮模型，利用仿真求解了復雜的傳質傳熱耦合固體收縮的干燥過程。但Murru 等[8-9]使用的蒸發速率常數為固定值，而實際干燥過程中的蒸發難易程度是會發生變化的，速率常數并非定值，越接近材料平衡含水率時蒸發越困難。

反應工程方法(REA)在常壓、高初始水含量材料的對流干燥過程仿真中已有廣泛應用[10-17]，該方法考慮了材料在不同水分含量時候的蒸發難易程度，并且考慮了材料平衡含水率的特性，具備良好的定量預測能力。Putranto 等[18]將REA 應用于高初始水分含量的食品真空干燥，證實了利用氣流干燥實驗所得到的參數在真空下仍然適用。本研究將REA 拓展應用于低初始水分含量的鋰電池真空干燥過程模擬，介紹該模型在實際生產中的參數對標和在線應用情況。

1 數學建模

1.1 鋰電池真空干燥簡介

軟包鋰電池主要包含3個部分：包裝袋、裸電芯和電解液。通常的生產過程是：在金屬基材(銅箔、鋁箔)上涂覆陽極、陰極漿料，經過隧道爐氣流干燥，其水分含量下降到小于1%，通常由于工序銜接存在時差，烘干的成卷極片會在干燥房中儲存一段時間(水分會略微減少)，之后取出分切為設計尺寸的陽極、陰極極片，再與隔離膜一起卷繞制成裸電芯。隨后在包裝工序將裸電芯放入鋁塑膜制成的包裝袋中，此時包裝袋留有一側開口未封裝，用于注入電解液。而注入電解液之前，電池需要放入真空干燥箱進行干燥，通常前期需要約2 h 利用熱氣流循環加熱把電池升高到所需的溫度，隨后抽真空，維持溫度與真空度。整個干燥過程一般需6～12 h，裸電芯的水分含量從500～2000 mg/kg 降低到150 mg/kg以下[1]。

1.2 真空干燥機理建模

電芯的卷繞結構較為復雜，陰陽極涂層具有多孔特性，鋁塑膜包裝袋與裸電芯之間存在空隙，這些空隙與多孔材料是連通的，干燥時顆粒蒸發的水蒸氣進入空隙，流經開口通道進入烘箱環境，最后被真空泵抽走。

水分的傳遞可分為四個過程：①裸電芯內部固體顆粒的水分蒸發到多孔介質孔隙區域；②多孔介質區域的水分傳遞到包裝袋空隙；③包裝袋空隙的水蒸氣進入烘箱環境；④真空泵對烘箱進行負壓抽吸，帶走水蒸氣。

由于實際生產每爐烘箱干燥的電芯數量多(幾百至上千)，很難直接耦合計算所有電芯的干燥過程。本研究結合實際進行合理簡化，假設每個電芯內部的干燥過程相同，所有電芯排放水蒸氣于烘箱共同空間內，由于真空狀態下氣體擴散極快，可認為烘箱空間中的水蒸氣濃度分布均勻。基于該假設，可簡化為只計算一個電芯的水分蒸發，而相應地，單電芯水分蒸發影響的有效烘箱空間體積=烘箱內部空間/電芯數量。

本研究采用商業軟件COMSOL 5.5，使用自定義方程建立兩組件模型求解(圖1)：對過程①～③使用模型組件1，利用三維(或零維，即集總參數模型)模型求解電芯固體材料干基含水率X(kg/kg)，本研究的鈷酸鋰材料體系電芯初始水含量700 mg/kg，對應初始干基含水率為7.0049×10-4；而過程④使用模型組件2，利用零維模型求解烘箱蒸汽濃度C(mol/m3)，其初始濃度為干燥房環境水分濃度，取值為0.00001 mol/m3。

圖1 真空干燥簡化模型Fig.1 Simplified model of vacuum drying

兩個組件相互耦合關系為：組件1 計算得到的電芯蒸發的水蒸氣量，作為組件2 的烘箱內部的水蒸氣輸入量；組件2所計算的烘箱環境水蒸氣濃度，作為組件1出口邊界的水分濃度條件。

模擬計算使用瞬態全耦合線性直接求解器，時間步進控制：向后差分公式方法、精確求解、初始步長0.0001 s、最大時間步長約束30 s，其他參數設置均使用軟件默認推薦。在線應用軟件開發使用COMSOL APP與Java編程實現。

1.2.1 質量守恒 裸電芯多孔介質區域與包裝袋包圍形成的空隙區域的氣體流場是連通的，多孔介質區域固、氣相水分質量守恒方程分別為固相

式中，hm為顆粒與氣相間的傳質系數，m/s；A為多孔介質比表面積，m-1；Cv,s為顆粒表面蒸汽濃度，kg/m3；Cv為顆粒附近環境蒸汽濃度，kg/m3；Cv,sat為飽和蒸汽濃度，kg/m3；ΔEv為蒸發活化能，J/mol。

式中，RHb為相對濕度。

相對活化能f(X-Xb)函數在常壓氣流干燥、高水分含量(＞2%，質量分數)材料已有較多實驗數據，用于描述蒸發的難易程度。當水分含量較多時，干燥容易進行，所以其值較小；當水分含量接近平衡含水率時，蒸發困難，曲線斜率快速增大，當其值為1時，顆粒表面蒸汽濃度與環境蒸汽濃度相等，蒸發停止。

根據Lin等[12]的實驗總結，一般的相對活化能方程為

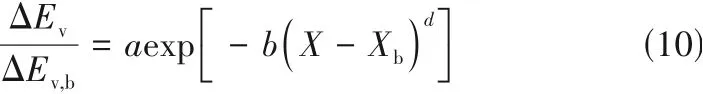
式中，a、b、d為一般材料的REA 模型參數。前人[11-18]所研究的相對活化能方程參數均在初始水含量較高的范圍(2%～50%)，而鋰電池的真空干燥的初始水分含量極低（500～2000 mg/kg，即0.05%～0.2%)，所以前人的參數在本研究中不適用。

根據高初始水分含量材料在氣流干燥下的REA 理論：脫離的材料水分從自由水到結合水轉變，干燥的相對活化能從0→1 變化(水分蒸發從容易→困難)，這種規律已經在食品、藥品等干燥上得到驗證[10-17]。陳曉東團隊[18]發現對于真空、高初始水分含量下的食品干燥，REA 模型參數仍具有良好的適用性。而高真空、低初始水分含量工況，雖然水分存在數量級差異，但通過類比方法推測這種規律依然存在。結合鋰電池真空干燥實驗數據，在公式中增加一個縮放參數進行嘗試，對(X-Xb)進行縮放，拓展現有模型參數的適用范圍，式(10)改寫為

式中，V為達西速度，m/s；F為重力(本研究可忽略)和其他體積力(本研究為多孔介質阻力)，kg/(m2·s2)；ρ為混合氣相密度，kg/m3；μ為動力黏度，Pa·s；ε為孔隙率；p為壓力，Pa；I為單位矢量；dp為平均顆粒直徑，m；κ為滲透率，m2。

1.2.4 環境濕度計算方法 關于烘箱水蒸氣濃度計算，假設微小時間內電芯蒸發出來的氣體體積等于真空泵從烘箱抽走的氣體體積，則烘箱平均水蒸氣濃度對時間微分得

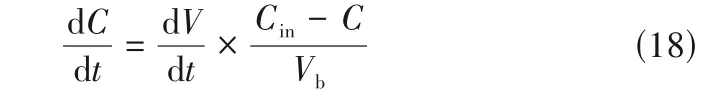
式中，C為烘箱平均氣體濃度，mol/m3；Cin為流入氣體濃度，mol/m3；Vb為烘箱體積，m3。

1.2.5 電芯溫升與環境壓力 實際電芯在真空干燥過程中，分為兩個階段。

第一階段：常壓氣流加熱，烘箱內部熱氣快速循環，把電芯加熱到設定溫度。

第二階段：真空恒溫烘烤，將電芯溫度穩定在設定溫度同時保持真空度。

本研究不模擬預測電芯的加熱溫升與環境壓力，而是直接使用實驗數據，為了簡化數據量，本研究2.1 節基于實驗測試簡化的電芯溫升與環境壓力曲線如圖2 所示。而在2.4 節實際量產應用則直接使用生產數據。

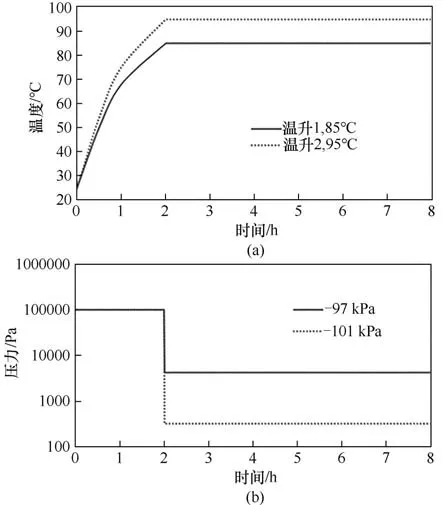
圖2 簡化的電芯溫升(a)與環境壓力對數(b)曲線Fig.2 Simplified temperature(a)and environment pressure logarithm(b)curve

2 仿真結果與討論

2.1 鋰電池真空干燥實驗

實驗材料：一種鈷酸鋰材料體系電芯(寧德新能源科技有限公司)。

實驗設備：真空干燥六面爐。

實驗方法：放置一定數量(滿載生產，通常數百個)的電芯在真空干燥箱中烘烤，每隔2 h 取電芯測量含水率(0，2，4，6，8 h)，每次測試3 個電芯，測量結果取均值；水含量測試方法為卡爾費休法[21]。

實驗條件：如表1 分組，共4 組，烘箱設備工作環境為20℃、環境相對濕度小于2%的干燥房中。電芯干燥過程中，2、4、6 h 取樣時需要打開烘箱門，相當于給電芯的烘箱環境進行換氣(呼吸)，對電芯邊界環境的水蒸氣濃度有稀釋作用。

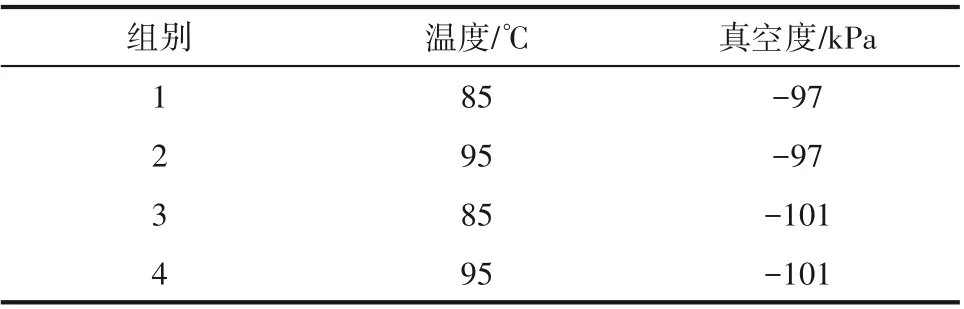
表1 真空干燥實驗組別Table 1 Experimental conditions of vacuum drying

2.2 仿真結果與實驗對比

本研究基于多孔介質模型，利用REA 表征水分蒸發動力學過程，為了準確定量預測干燥終點，材料平衡含水率(Xb)是重要的影響因子，本研究使用的平衡含水率方程參考了文獻[22]，認為在較小的溫度范圍內平衡含水率僅是相對濕度的函數[23]，通過實驗數據標定材料的平衡含水率表達式為

Xb= 0.0002981RH0.2871b(19)

而實際上，平衡含水率與材料本身的成分、密度、粒徑、比表面積等相關[24-25]。鋰電池的陽極、陰極、隔離膜，本身都是由不同配方的材料組成，其平衡含水率特性是所有材料特性的疊加。同時，不同的生產工藝，顆粒的空間分布有差異，導致材料透氣孔隙會相互覆蓋[25]，再加上溫度、濕度兩個因子，很難擬合出一個通用的公式來涵蓋所有變量的影響。本研究把電芯簡化為一種均勻組分，在配方不變、生產穩定的情況下，選擇與生產最直接相關的因素，能夠讓平衡含水率模型在合適的溫度、濕度內滿足預測精度要求。

本研究在真空干燥仿真中，考慮了換氣動作。圖3 展示了電芯的干燥曲線與實驗數據的對比結果。圖4展示了電芯內部的水蒸氣平均分壓變化曲線。從圖4 中可以看到，在烘箱進行換氣動作時(2，4，6 h)，烘箱內的水蒸氣的分壓大幅下降，對應圖3中水含量曲線的斜率突變點。在2 h 時刻的水含量突變最顯著，其原因是該時刻電芯溫度已達到最大值，烘箱由常壓狀態轉變為真空狀態，該狀態下電芯水分含量充足、蒸發的相對活化能低，蒸發速率為瞬時最大值。

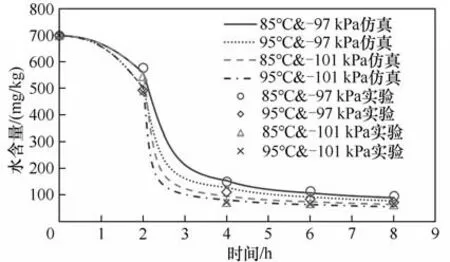
圖3 仿真模擬的干燥曲線與實驗數據對比Fig.3 Comparison of the simulated drying curve and experiment data

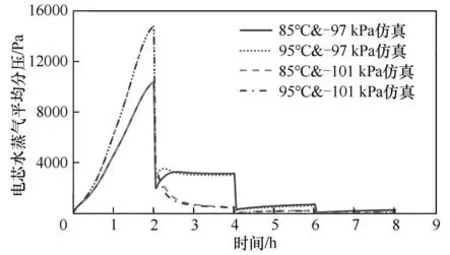
圖4 不同條件下電芯水蒸氣平均分壓對比Fig.4 Comparison of the average vapor pressure in the cell under different conditions

圖5展示了干燥過程中固體與氣體中水分場的變化過程(僅展示組別1 的結果，其他組別規律均類似，不再贅述)。從云圖上可看出電芯干燥過程中不同位置的固體水分差異不大，基本上是均勻的，而氣相水分場除了循環干燥階段濃度存在較小偏差外，真空干燥階段濃度也是均勻的。而實際上在真實的干燥狀態下，電芯氣袋口是敞開的，裸電芯內部的層與層之間也是相對疏松透氣的，因此在真空狀態下電芯內的水分擴散極快。基于此特征，后續在實際生產應用中，可以將三維模型進一步簡化為零維來提升計算效率。

圖5 固體/氣體中水濃度云圖(組別1：85℃&-97 kPa)Fig.5 Moisture contour of solid and gas phase(Group1：85℃&-97 kPa)

表2 是對圖3 數據進行的統計學的偏差分析，4 種實驗條件下的相關系數都達到了0.998 以上，表明仿真對干燥趨勢的預測較為準確。均方根誤差最大值為13.09409，平均相對誤差最大值為0.08872，偏差分析結果表明仿真偏差小于10%。而基于卡爾費休法的實驗測試誤差本身波動就比較大，容易受環境濕度與操作人員制樣熟練度影響，通常在測試均值為100 mg/kg情況下波動約±15 mg/kg，所以相比之下，仿真的精度在可接受范圍之內。

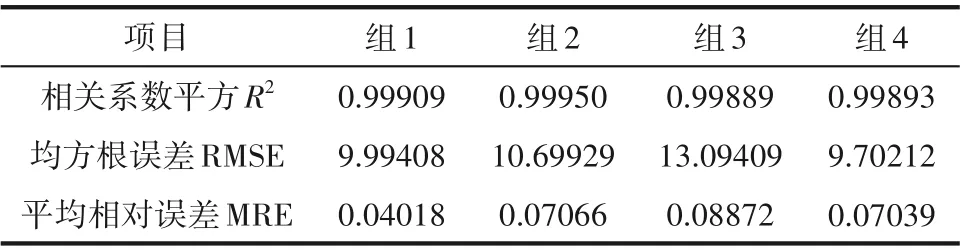
表2 偏差分析Table 2 Deviation analysis

2.3 干燥規律仿真預測

本節基于2.2 節所建立仿真模型，通過調整其關鍵變量進行單因子探索研究。根據生產經驗，表3列出了關鍵參數的初始值。

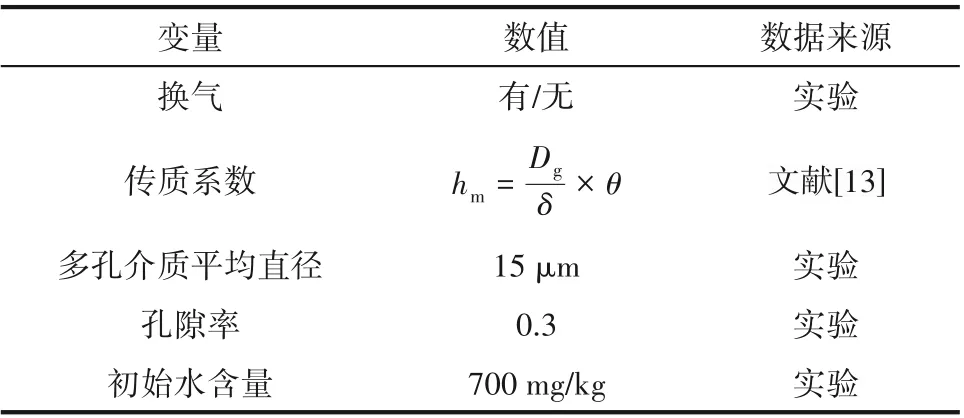
表3 關鍵變量初始值Table 3 Initial value of characteristic variable

2.3.1 換氣影響 在實際生產中，真空干燥六面爐烘箱的恒溫真空干燥階段，存在多次“呼吸”換氣動作。本次實驗存在三次換氣，第一次為常壓轉為抽真空，后面兩次為保持真空階段的“呼吸”換氣。本研究對比了當取消真空階段兩次換氣對水含量圖（6）和電芯內部的水蒸氣分壓（圖7）的影響。

圖6、圖7結果表明，在真空干燥過程中，對烘箱進行“呼吸”換氣，可以使電芯水分蒸發更快，終點水分含量更低。根據式(3)，環境濕度越低，水分濃度差值越大，推動力越大；同時低濕度對應的材料平衡干基含水率越低，電芯能夠干燥到更低的水分含量。

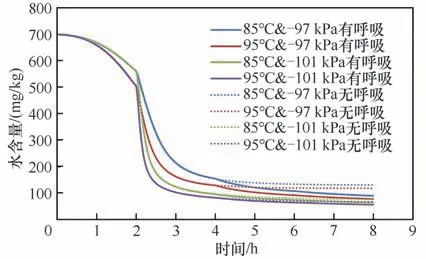
圖6 有無“呼吸”換氣動作對干燥的影響Fig.6 Effect of breathing action on drying process

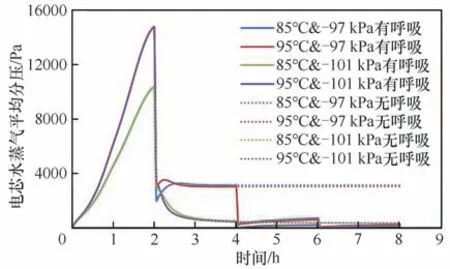
圖7 有無“呼吸”換氣動作對電芯水蒸氣分壓的影響Fig.7 Effect of breathing action on vapor pressure in the cell

通過對比低真空度(-97 kPa)與高真空度(-101 kPa)的仿真結果，可以發現“呼吸”作用在不同真空度的影響程度不同：高真空度時，烘箱環境的分壓已經極低，而水分的分壓最多也就325 Pa；而低真空度，水分的分壓最高可以達到4325 Pa。所以低真空度下，“呼吸”操作的影響很大，可以稀釋環境中的濕度。實際生產中，由于每次的破真空與抽真空有可能對電芯的溫度有影響(本研究未考慮)，低真空度的真空干燥設置合適的間歇呼吸次數與時間，尤其是在烘箱內濕度較高的干燥前期，能夠最大程度地提高干燥效率。

2.3.2 傳質系數影響 通過對式(6)傳質系數hm進行簡單的縮放研究，觀察其影響規律，得到如圖8所示仿真計算結果。結果表明，傳質系數越大，水分干燥得越快。而實際生產中，采用高真空度，或者高溫，都可以提高氣體的擴散系數Dg，從而提高傳質系數hm來加快干燥，該規律與仿真結果相符。

圖8 傳質系數對干燥的影響Fig.8 Effect of mass transfer coefficient on drying process

2.3.3 顆粒平均直徑影響 本研究把電芯極片等效為多孔材料，其顆粒平均直徑是等效簡化數值。圖9 為顆粒直徑對干燥過程的影響模擬結果，干燥速率隨平均直徑增加而減小。根據比表面積計算式式(7)可知，當顆粒的平均直徑增加，傳質面積減小，所以模擬預測的干燥速度減小，而8 h 時刻干燥的終點水分含量增加。

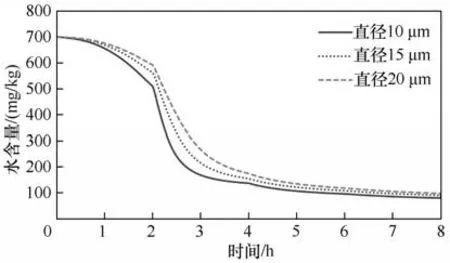
圖9 顆粒平均直徑對干燥的影響Fig.9 Effect of average diameter of porous media on drying process

2.3.4 孔隙率影響 圖10 展示了電芯極片多孔材料孔隙率的影響規律，仿真結果表明，當顆粒的孔隙率增加，干燥速度加快。其主要原因是，孔隙率增加后，傳質比表面積增加，同時多孔材料的透氣度也提高，有利于水分的快速蒸發擴散。

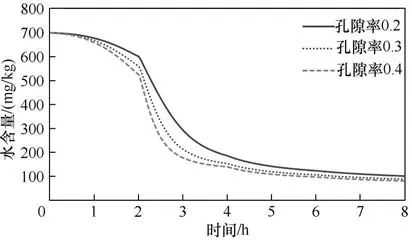
圖10 孔隙率對干燥的影響Fig.10 Effect of porosity of porous media on drying process

2.3.5 初始水含量影響 圖11 展示了電芯初始水含量的影響規律，結果表明，初始水含量越大，干燥前4 h，電芯水含量差別較大；但當電芯干燥到4～8 h階段，電芯的水分含量均已較低且數值十分接近，仿真預測的終點8 h差別小于5 mg/kg。這種特性是材料的蒸發能力所決定的，高水分含量蒸發較快，而低水分含量時干燥困難、蒸發較慢。基于該仿真規律，可以推斷出該材料類型電芯的初始含水率對干燥終點影響不大，而實際生產應用中，則無須耗費過多資源去監控生產工序來料電芯的初始水含量。

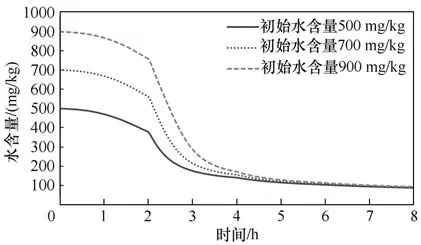
圖11 電芯初始水含量對干燥的影響Fig.11 Effect of battery initial moisture on drying process

2.3.6 零維模型與三維模型對比 工業在線應用對仿真計算的效率要求很高，結合前文討論，不考慮三維流場流動、多孔傳輸阻力等因素，可把REA干燥模型簡化為均質的零維模型，其中需要注意的是蒸發傳質總面積=多孔材料比表面積×體積。

圖12為零維和三維模型仿真結果對比，結果表明兩個模型預測基本沒有差別，這是由于真空狀態下，材料內部的傳質效率極快，不同幾何位置差異很小。而兩個模型的計算時間則呈現出數量級的差異，在工作站平臺(Intel Xeon E5-2697A V4 雙路32 核，256G 內存)，三維模型耗時806 s，零維模型僅耗時17 s。相比之下，高效的零維模型更適合在線仿真預測。

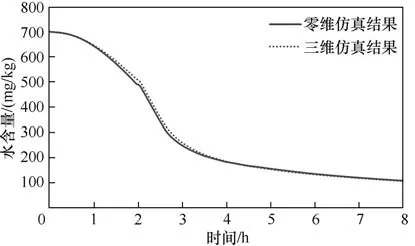
圖12 零維模型與三維模型干燥仿真結果對比Fig.12 Comparison of drying simulation results between 0-D model and 3-D model

2.4 量產應用介紹

目前，作者團隊已實現了基于REA 的水含量預測軟件(零維)的開發，并實現了量產應用。

在量產的設備中，有一種最新的采用接觸式加熱的真空干燥爐，其爐內絕對氣壓能夠控制在100 Pa 以下，相比于普通六面爐干燥效率更高、干燥時間更短，并且該設備生產時，電芯的溫度、爐箱壓力數據都可以實時在線獲取，而設備的這些功能特性是水含量在線預測得以實現的重要保證。

相比于真空度不高的普通六面爐工況，這種高真空條件下的參數對標(平衡含水率、相對活化能曲線)反而要簡單得多。結合式(3)，在絕對氣壓低于100 Pa 的情況下，可近似認為箱體的氣體完全為水蒸氣，而實測的壓力數據即可代表環境水蒸氣濃度Cv；同樣，根據相對活化能方程式(8)，在絕對氣壓低于100 Pa 的情況下，電芯在不同的溫度干燥的時間足夠久[24-25]，即可認為達到其平衡含水率Xb。

2.4.1 參數對標條件與結果 選定一種鈷酸鋰電芯進行參數對標，實驗方法與2.1 節基本相同，干燥過程為：常壓加熱0.42 h；隨后抽真空，進行恒溫真空干燥。

圖13(a)展示了三種工況(目標溫度75，85，95℃)下電芯的干燥溫度數據，圖13(b)展示了對應的干燥爐箱體環境絕對壓力數據。從溫度與壓力曲線上看，存在一些突變點，這些數據波動是由于人工取樣測水含量導致（取樣時箱體需要破真空，時間小于1 min）。

圖13 鈷酸鋰電芯的溫升(a)與環境壓力對數(b)曲線Fig.13 Temperature(a)and environment pressure logarithm(b)curve

由圖13(b)中壓力數據可看到，氣壓是在20～100 Pa 之間往復反彈，這是設備本身的控制策略所決定的，其壓力變化率一定程度也反映了水分的蒸發速率。實際情況可能還會更復雜，因為設備密封能力不同，會使得壓力曲線數據存在差異。觀察數據不難發現，在三種溫度工況下，電芯所處的環境壓力基本可認為相同。表4展示了在基本相同的環境壓力下，在設定溫度維持足夠長的時間后得到的電芯的平衡干基含水率Xb，結果表明溫度對平衡干基含水率的影響十分顯著，這是材料本身的蒸發能力所決定的一種固有屬性。

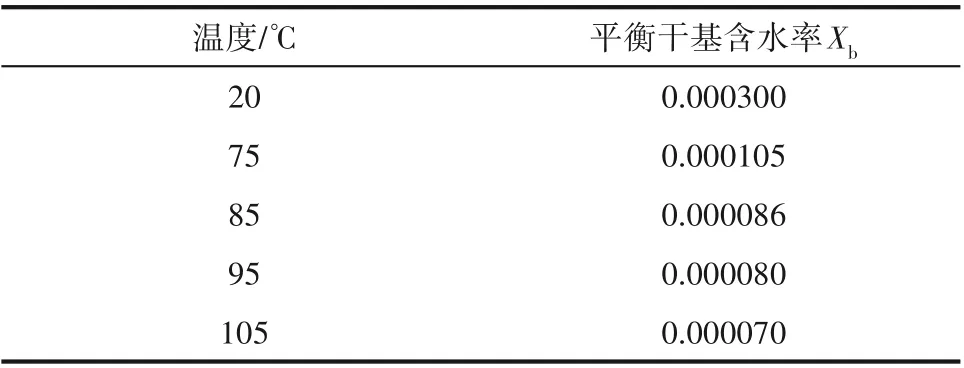
表4 鈷酸鋰電芯的平衡干基含水率Table 4 Equilibrium moisture content（dry basis）of lithium cobalt oxide battery

利用實驗干燥曲線數據與平衡含水率數據，結合REA 理論，參考文獻[12]方法，可以反求電芯的相對活化能曲線。圖14 是求解得到的鈷酸鋰電芯的相對活化能曲線。同2.2 節中關于材料組分疊加平衡含水率的討論，不同材料的相對活化能特征曲線存在差異，而本研究得到的相對活化能曲線亦是所有材料組分疊加后的曲線，在配方不變、生產穩定的情況下具有良好的適用性，這個規律在不同尺寸、相同配方工藝的電池干燥實驗中已經得到驗證。

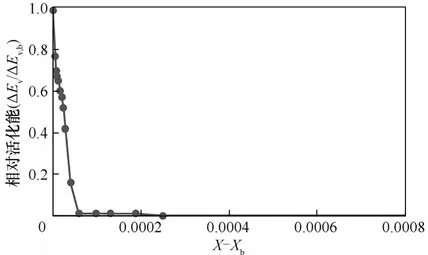
圖14 鈷酸鋰電芯的相對活化能曲線Fig.14 Relative activation energy curve of lithium cobalt oxide battery

從相對活化能曲線中可以明顯看到，鈷酸鋰電芯在高水分含量的情況下相對活化能極小(≈0)，干燥極快；而在低水分含量時相對活化能急劇升高，干燥速度大幅下降。圖15 的預測曲線清晰呈現了電芯的干燥過程，顯著地反映了材料相對活化能曲線的特征。高水含量階段干燥速率極大、時間很短，而后續水分干燥困難，耗費了大部分的干燥時間，基于此可以推斷電芯的初始含水率對干燥終點預測結果影響不大，這與Langklotz 等[24]報道的結論一致，而量產測試結果也證實了該結論。因此，同2.3.5 節結論，只要實際生產條件波動不是很大，無須頻繁監控初始水含量。

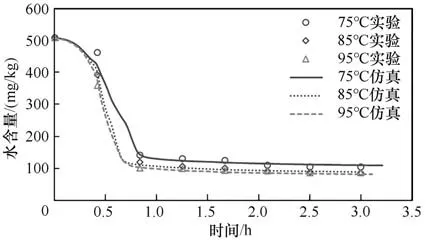
圖15 鈷酸鋰電芯水含量仿真預測與實驗結果對比Fig.15 Comparison of moisture content prediction and experimental result of lithium cobalt oxide battery

2.4.2 實驗驗證與量產驗證 基于2.4.1 節標定后的參數，在更多的實驗條件下進行對比，進一步確認預測精度。表5 展示了驗證結果，在不同溫度與干燥時間設定下，實測值與預測值匹配良好，預測平均偏差為6.6 mg/kg，證明了干燥REA 在鋰電池真空干燥中具有良好的預測精度。

表5的數據呈現出一個現象：水含量較高時，均為正偏差。一方面是由于干燥初始階段水含量較高時，水分蒸發較快，與圖15中30～65 min干燥曲線斜率很陡一致，加上設備取樣、制樣等時間控制誤差較大，測試誤差也相對較大。而另一方面從電芯環境濕度看，該階段水分蒸發較快，環境濕度高，基于簡化模型假設，微小時間內電芯蒸發出來的氣體體積等于真空泵從烘箱抽走的氣體體積(1.2.4 節)，而實際設備空間較大(1～2 m3)，導致真空設備排濕有一定的時間延遲，所以實際環境濕度會略高于仿真計算值，所以實際值為正偏差。而生產更關注干燥后續終點水含量，因此該階段偏差在可接受范圍內。

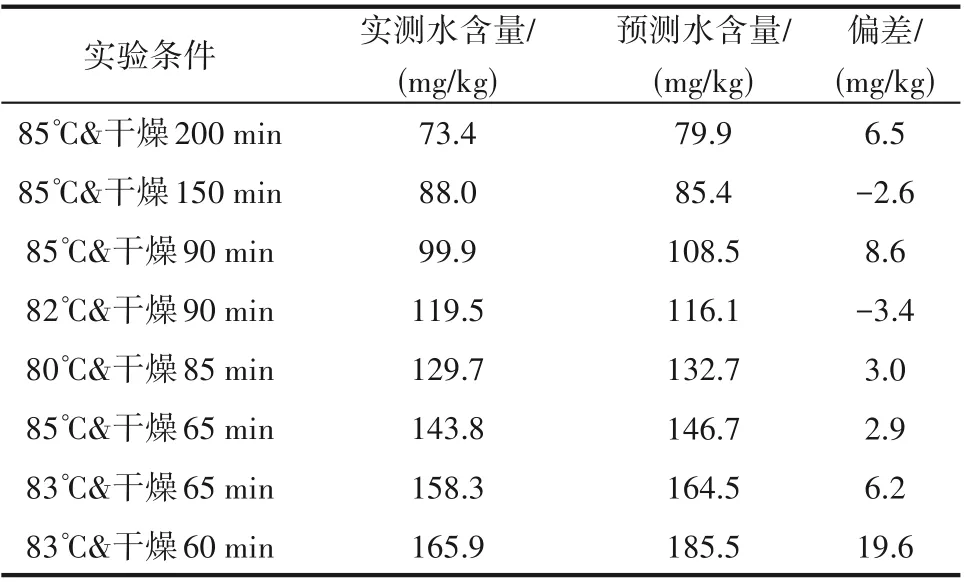
表5 不同實驗條件下實測與預測水含量對比Table 5 Comparison of measured and predicted moisture content under different experimental conditions

更進一步，開發了基于干燥REA 的預測算法程序，在量產實現了在線預測應用。一種鈷酸鋰電芯的在線應用結果如圖16 所示，共統計了36 批次樣品，其預測精度滿足小于10%的生產要求。圖中可以看到量產中的水含量波動比對標實驗要大一些，原因一方面是測試誤差，基于卡爾費休法的測試很容易受環境濕度與操作人員制樣熟練度影響；另一方面是不同量產設備之間存在一些固有的系統誤差。

圖16 量產實測與預測水含量對比Fig.16 Comparison of measured and predicted moisture content in mass production

另外，在線預測也已經逐步推廣應用到磷酸鐵鋰和三元體系電芯的真實干燥中，圖17為兩種材料體系的對標驗證結果，此處不再贅述。

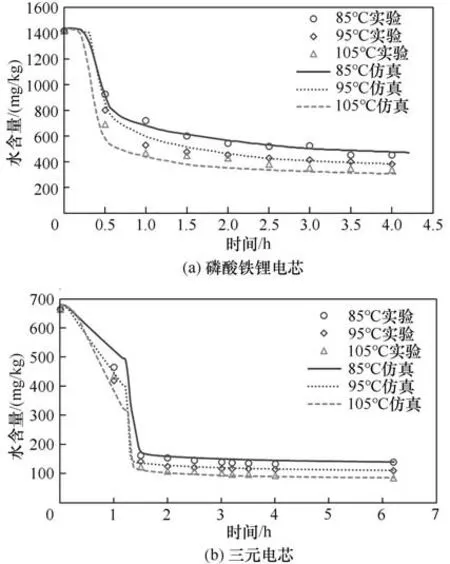
圖17 磷酸鐵鋰電芯(a)與三元電芯(b)水含量仿真預測與實驗結果對比Fig.17 Comparison of moisture content prediction and experimental result of lithium iron phosphate(a)and ternary lithium battery(b)

3 結 論

本研究利用多孔介質模型對電芯材料進行簡化，并將反應工程干燥理論應用于鋰電池的真空、低初始水含量的干燥過程仿真。利用該方法求解了不同溫度、真空度的干燥過程，得到的仿真結果與實驗結果匹配良好，最大偏差小于10%。基于該模型，進行了一系列的單因子影響仿真分析，如烘箱換氣、傳質系數、顆粒平均直徑、孔隙率、初始含水率等，仿真得到的規律均與實際生產中的現象與經驗認知相符合。

目前，基于反應工程方法的預測軟件已開發完成，并且在鈷酸鋰電芯的量產中應用，另外也已經逐步推廣應用到磷酸鐵鋰和三元體系電芯的真空干燥中。而未來，完善不同材料體系的參數庫，進一步細化陰極、陽極、隔離膜各自的材料特征屬性參數，反應工程方法將在鋰電真空干燥有更好的應用價值，指導工藝改善，提高生產效率、提升品質、降低成本。

符 號 說 明

A——多孔介質比表面積，m-1

a,b,d——材料的REA模型參數

C——烘箱平均氣體濃度，mol/m3

Cin——流入氣體濃度，mol/m3

Cv——顆粒附近環境蒸汽濃度，kg/m3

Cv,s——顆粒表面蒸汽濃度，kg/m3

Cv,sat——飽和蒸汽濃度，kg/m3

c——材料的REA模型參數，縮放系數

Dg——水分在氣相中的擴散系數，m2/s

Ds——水分在固相中的擴散系數，m2/s

dp——多孔材料的平均顆粒直徑，m

ΔEv——蒸發活化能，J/mol

ΔEv,b——平衡蒸發活化能，J/mol

F——重力和其他體積力，kg/(m2·s2)

hm——顆粒與氣相間的傳質系數，m/s

I——單位矢量

I˙——水分蒸發源項，kg/(m3·s)

p——壓力，Pa

RHb——相對濕度

T——溫度，K

V——多孔區域達西速度(非多孔區域氣體流動速度)，m/s

Vb——烘箱體積，m3

X——材料干基含水率，kg/kg

Xb——材料平衡干基含水率，kg/kg

δ——傳質厚度，m

ε——孔隙率

θ——材料特征系數

κ——滲透率，m2

μ——動力黏度，Pa·s

ρ——混合氣相密度，kg/m3

ρw,g——氣相中水蒸氣密度，kg/m3

ρw,s——固相中水分密度，kg/m3