蒸汽冷凝近壁過渡區團簇演化特性

李雯，蘭忠，強偉麗，任文芝，杜賓港，馬學虎

（1 大連理工大學化學工程研究所，遼寧 大連 116024； 2 內蒙古北方重工業集團有限公司，內蒙 古包頭 014000）

引 言

冷凝成核現象廣泛存在于自然界及生產生活中，如車窗上的白霧，生物表面的結露[1-2]，以及工業領域中的熱管理[3-4]、水汽捕集[5]、熱電系統[6]、海水淡化[7-8]等。對成核過程的演化規律和機理的深入研究，不僅可以為冷凝過程的調控提供指導，還有助于完善蒸汽冷凝換熱過程的基礎理論。

關于成核過程的機制，1935 年，Tammann 等[9]提出固定成核中心假說，認為蒸汽在壁面冷凝時，氣相中的水分子首先在壁面上的成核位點處核化。隨后，研究者們通過大量的實驗觀察和理論分析[10-13]證明了該假說的合理性，但該假說并未描述蒸汽分子靠近壁面以及形成最小核化液滴之前所經歷的物理過程，這也使得大部分針對凝結過程或核化過程的調控技術，主要關注在壁面微納功能結構或成核位點的設計上。宋天一等[14]通過濕空氣露點冷凝的可視化實驗，發現冷凝表面上初始液滴尺寸分布符合對數正態分布，再結合分子團聚理論[15]，反演推知氣相分子在壁面沉積之前已經在近壁空間中形成了團簇分布，從而提出了水分子在壁面上冷凝核化前會預先在近壁空間中團聚生成團簇的冷凝團聚物理模型。Lan 等[16]將上述冷凝團聚物理模型與滴狀冷凝傳熱模型相聯系，并分析了不凝性氣體由于影響了團簇分布而極大影響了凝結換熱效率的機制，通過將模型計算結果與文獻中的實驗數據對比進一步證實了模型的合理性。自此，近壁空間中的團簇作為成核前冷凝介質的存在狀態開始進入研究者們的視野，對它的更為全面和深入的研究無疑是成核調控中的重要一環。

為了探究蒸汽冷凝核化前氣相團簇的演化分布規律，并且考慮到傳統的觀測手段，如高速攝像和顯微鏡放大，難以觀測發生在納米和納秒層面上的團簇演化，Lan等[17]利用瑞利散射原理，通過測量距離過冷壁面不同高度位置的散射光強來反映空間中團簇的分布，但鑒于瑞利散射光強受團簇尺寸與數密度的共同影響，更多的與空間團簇分布相關的細節，比如空間溫度的變化以及團簇的形成機制還不清楚。近年來，越來越多的學者借助分子動力學（molecular dynamics,MD）模擬的手段來研究蒸汽在冷卻表面上的成核物理過程，也鑒于對成核前近壁區分子團簇演化物理圖景的缺乏，他們的工作也主要集中在壁面親疏水性[18-20]，表面結構的形狀、尺寸和排布[21-22]，壁面過冷度[22]，外場[23]，不凝氣[24-25]等對壁面上的成核位置，團簇大小、數量、形狀以及冷凝傳熱效果的影響。但不容忽視的是，對氣相團簇分布演化的深入研究有望從“氣液相變的初始狀態”這個最早的階段出發來完善成核過程的演化規律和理論，并為實際工程中的冷凝過程調控提供新的思路和指導。

分子模擬的尺度一般為納米級，而從實驗初步觀測結果可以看出，近壁團簇演化分布范圍為幾百微米[17]，文獻中常見的壁面-水冷凝的MD 模型無法直接用來研究整個近壁空間的團簇情況。因此，本文根據文獻[17]中實驗表明的冷凝達到穩態（定態）時，近壁空間形成一定團簇尺寸分布這一特點，從唯象角度，將處于近壁空間中某區域的近平衡態視為其中團簇處于熱力學平衡狀態，那么實際上該區域就處于一定的過飽和度，將相對宏觀的近壁空間抽樣成多個納米尺度上的均相體系，并根據不同高度對應的團簇尺寸（也即過飽和度或蒸汽溫度）不同，將近壁區團簇隨離壁距離的分布曲線抽樣成多個不同溫度下的均相水體系冷凝模型，最后通過整合不同高度處的團簇演化特征，綜合獲得宏觀近壁空間中的團簇演化構象和分布規律。在此基礎上探究了蒸汽壓力以及不凝氣對近壁空間團簇分布的影響和作用機制。

1 近壁團簇分布規律MD 分析模型的構建

鑒于所研究物理問題是距離壁面幾百微米的近壁空間中的團簇的演化分布，常規MD 方法很難實現。因此結合已有的理論和實驗研究成果[17,26]，如圖1所示，將近壁空間中團簇分布看作是唯象的，那么顯然當冷凝過程達到穩態時，空間局部位置即可看成近平衡態，雖然團簇是可移動的，它可能會在壁面上徙動、分裂或蒸發，以及可能離開壁面或在近壁區擴散，但終將形成一個“穩定”分布，換句話說，近壁空間中某個位置對應一定尺寸及分布的團簇，而唯象角度可認為該位置的團簇處于熱力學平衡。或者考慮這樣的唯象分布狀態，因為平衡態與過程無關，這樣的團簇分布雖然可能是擴散等機制形成的，但也可以認為是水分子直接在近壁空間對應位置處于熱力學平衡而得到的。再從另一個角度看，當冷凝過程處于定態時，壁面與體相間存在溫差ΔT（即過冷度），但這種溫差通常可理解為并非突變形成，而是在近壁較小空間中以某種漸變曲線方式形成。換句話說，近壁空間中有一個溫度漸變的過程，因此與溫度變化對應也將具有過飽和度變化的過程。特別要指出的是，通常在傳熱領域普遍接受近壁區（或者說邊界層）溫度是漸變的這個概念，但具體溫度是如何漸變的，或者最需要強化的區域在哪里，并不清晰。因此可以將近壁區進行抽樣分析，不同的過飽和度（用與蒸汽體相間的溫差δT表示）代表不同的離開壁面的距離（但目前為止并不知道距離多遠對應多大的過飽和度），通過分析不同δT（對應空間中不同高度位置）下團簇的演化分布特征來構建整個近壁空間的分布特征。這樣一來，宏觀尺度的過冷壁面上的非均相冷凝過程的近壁區，就可以借助分子動力學模擬通過均相體系在多個不同過冷溫度δT下的演化來描述。

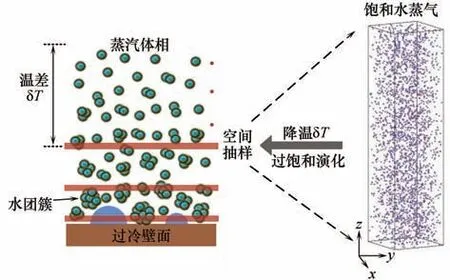
圖1 近壁幾百微米空間中團簇分布演化的研究方法的示意圖和初始模擬體系的構建Fig.1 Schematic of research method for cluster distribution evolution in hundreds of microns space near subcooled wall and setup of the initial simulation system

根據上述分析來構建分子動力學模擬的具體模型，首先，選擇TIP4P/2005模型[27]來表征水分子間的相互作用，它在描述與水冷凝相關的物性參數方面表現出較高的精度，在該模型中，H-O-H 平分線上距O 原子0.1546 ?(1 ?=0.1 nm)處設有一虛擬位點，帶1.1128 e 的負電，兩個氫原子分別帶0.5564 e的正電，氫氧鍵長為0.9572 ?，鍵角為104.52°，相應的水分子間相互作用勢的表達式如下：

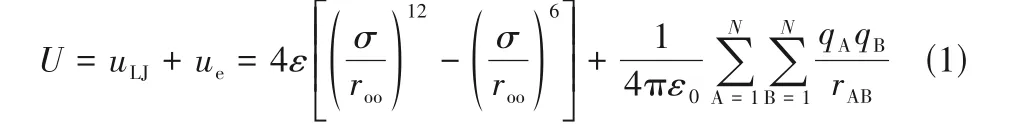
式中，U是水分子間的總勢能，由兩部分組成。第一部分的uLJ為短程范德華作用勢，其中ε為勢阱深度，代表兩個原子間相互作用的強弱，σ為Lennard-Jones(LJ)勢能等于0 時原子間的距離，對于氧原子有ε=0.1852 kcal/mol(1 kcal=4.18 kJ)，σ=3.1589 ?，roo為兩個氧原子之間的距離。第二部分的ue為靜電作用勢，其中ε0為真空中的介電常數，qA為A 作用位點所帶電量，qB為B 作用位點所帶電量，rAB為A、B 兩帶電作用位點間的距離。因為水分子間的相互作用相比其他簡單粒子多了靜電力的影響，所以計算時更為復雜和費時，因此在構建初始模擬體系時，為了滿足形成臨界液核所需的分子數同時提高計算效率，選定初始溫度T0為423 K的飽和水蒸氣體系,且體系尺寸為lx×ly×lz=20 nm×20 nm×79 nm，再根據423 K下飽和水蒸氣的密度為2.54 kg/m3，計算可得體系共包含2684個水分子，如圖1所示。

2 模擬細節設置

選用大規模原子/分子并行模擬器（large-scale atomic/molecular massively parallel simulator,LAMMPS）進行分子動力學模擬，體系的x、y、z三個方向均設置周期性邊界條件，運動方程的積分選用Velocity-Verlet算法，時間步長為1 fs。對LJ相互作用采取截斷處理且截斷半徑設置為10 ?，長程靜電力的處理選用PPPM (particle-particle-particle mesh)算法，模擬在NVT 系綜下進行，使用Nose-Hoover 調溫器來控制體系溫度。

模擬具體分三個階段進行，首先通過能量最小化對體系結構進行優化，防止在初始階段局部受力過大而造成體系崩潰,優化的收斂標準根據文獻[18]制定為直到體系中任何原子在任何方向上的受力小于1.0×10-6kcal/(mol·?)。然后，進行第一次NVT系綜下的模擬，控制體系溫度為初始飽和水蒸氣體系對應的飽和溫度，即T0=423 K，弛豫總共150000時間步，即150 ps，讓體系在初始溫度下稍微平衡一下，形成一個初始飽和溫度下正常的隨機分布，溫度的控制使用Nose-Hoover 控溫方法。最后，進行第二次NVT 模擬，第一次NVT 模擬結束后，緊接著降低體系溫度使Ti＜423 K，讓水分子繼續在Ti下演化直到平衡。為了對應距離壁面不同高度的位置，本文共模擬了九個體系，分別降低不同的溫度δT=100,60,50,40,30,25,20,15,10 K，由于體系溫度降低后水蒸氣會進入過飽和狀態，隨著模擬的進行，體系中水分子團聚生成團簇，團簇不斷生長、合并、分裂，直至達到對應溫度下的平衡狀態。使用Ovito、Vmd、Origin 以及Matlab 軟件對模擬進行可視化觀察以及數據的提取和分析。

3 結果與討論

3.1 純蒸汽條件下近壁空間中團簇的演化構象和分布規律

首先，以δT=50 K 體系的分子動力學模擬為例來進行簡單說明，圖2 顯示了體系溫度隨模擬時間的變化，從圖中可以看到體系初始溫度和降低50 K后溫度基本都在設置的溫度值附近波動，表明模擬確實是按照所控制的溫度進行的。圖3(a)顯示了隨著時間的進行，體系能量E不斷減小最終趨于穩定,這是因為隨著模擬的進行，在過飽和的條件下，體系中的水分子逐漸凝結形成團簇并且團簇隨時間在不斷長大，期間也伴隨團簇的合并與分裂,如圖3(b)的模擬快照圖所示。

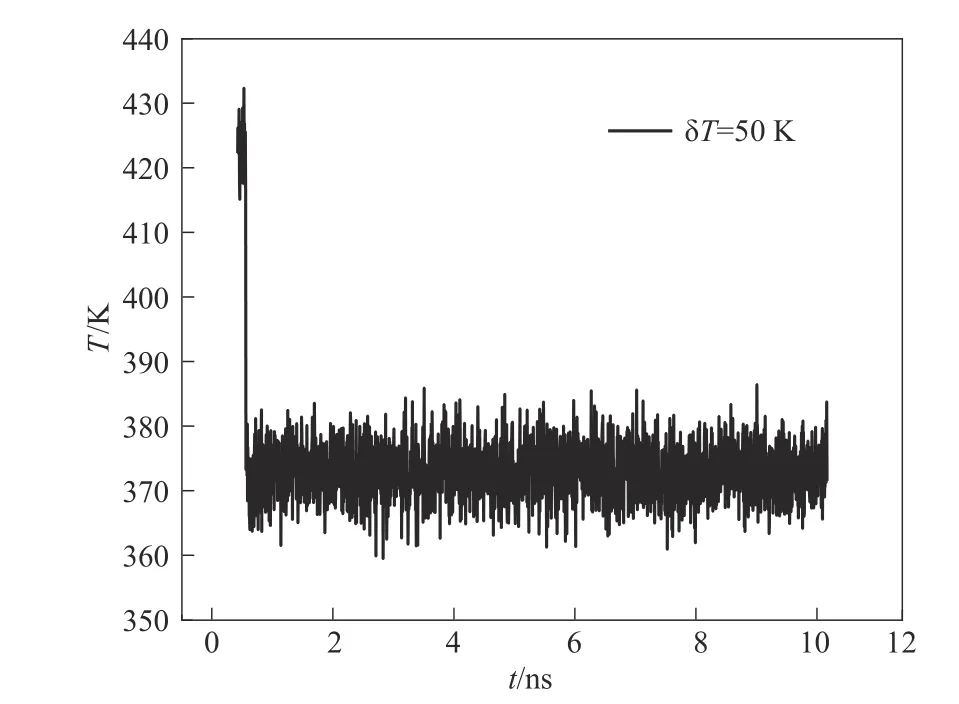
圖2 δT=50 K體系的溫度隨模擬時間的變化Fig.2 Variation of system temperature with time for δT=50 K

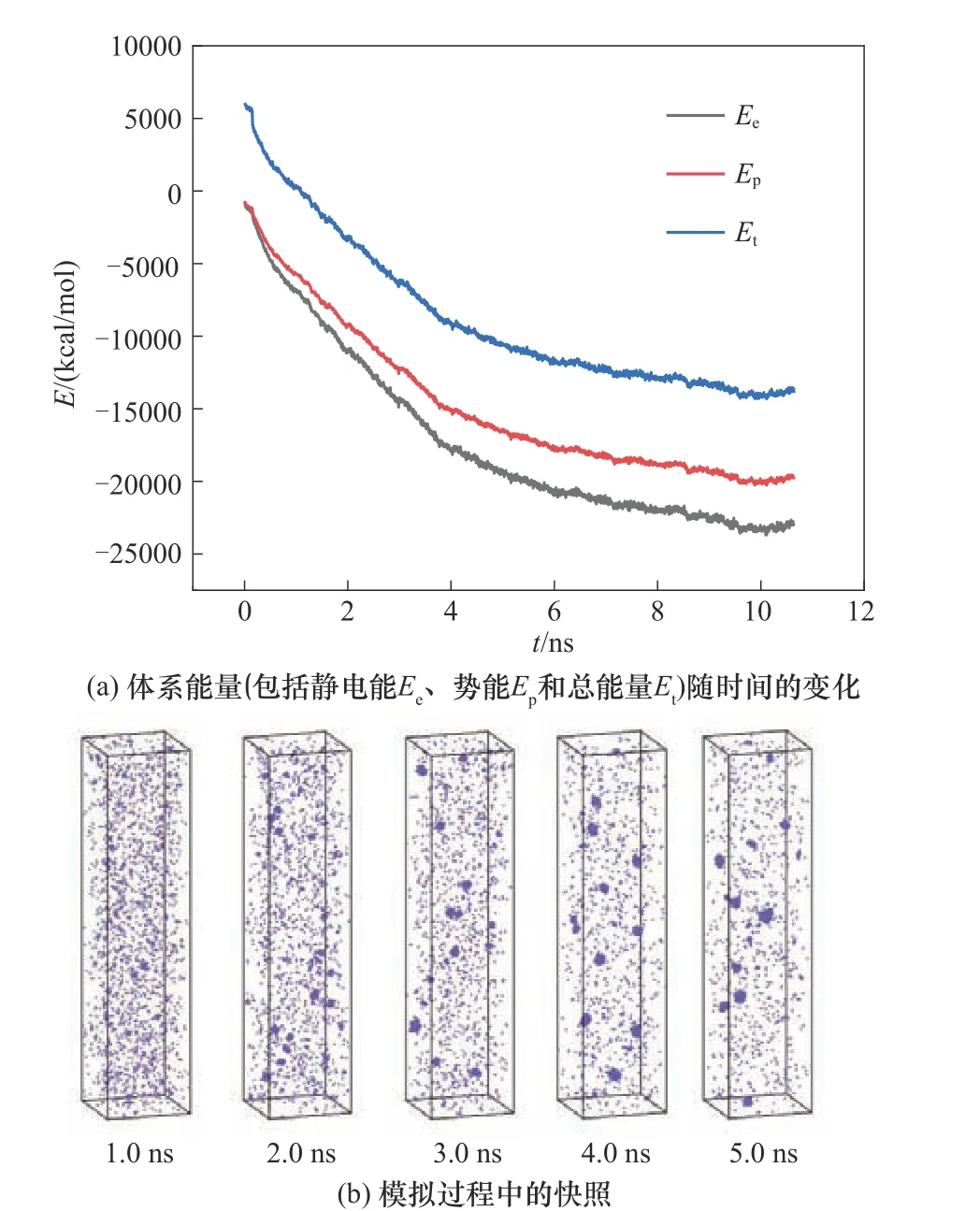
圖3 δT=50 K時的模擬過程變化Fig.3 Variations during the simulation process for system of δT=50 K

為了比較不同δT體系中水分子的團聚情況，首先分析了不同δT體系的勢能隨時間的變化，如圖4(a)所示，可以發現，對于所有的δT體系，由于水蒸氣分子團聚形成團簇，體系勢能值隨時間不斷減小，并最終達到穩定，勢能曲線下降的快慢表明了團簇演化的快慢，可以看到δT越大，即距離過冷壁面越近，水分子團聚越快。隨后，基于Stillinger距離判據[28]對體系中生成的團簇進行了識別和統計，當某個水分子中的氧原子與鄰近團簇中的任何一個水分子中的氧原子之間的距離小于3.36 ? 時，認為該氧原子所在的水分子便屬于該團簇，利用Matlab編程，通過讀取模擬獲得的軌跡文件，統計得到不同δT下不同時刻的團簇大小和數目信息，結果如圖4(b)所示。從圖中可以看到對于不同的δT總團簇分子數均隨時間不斷增大，最終穩定，并且δT越大，生成的團簇所包含的分子數越多。

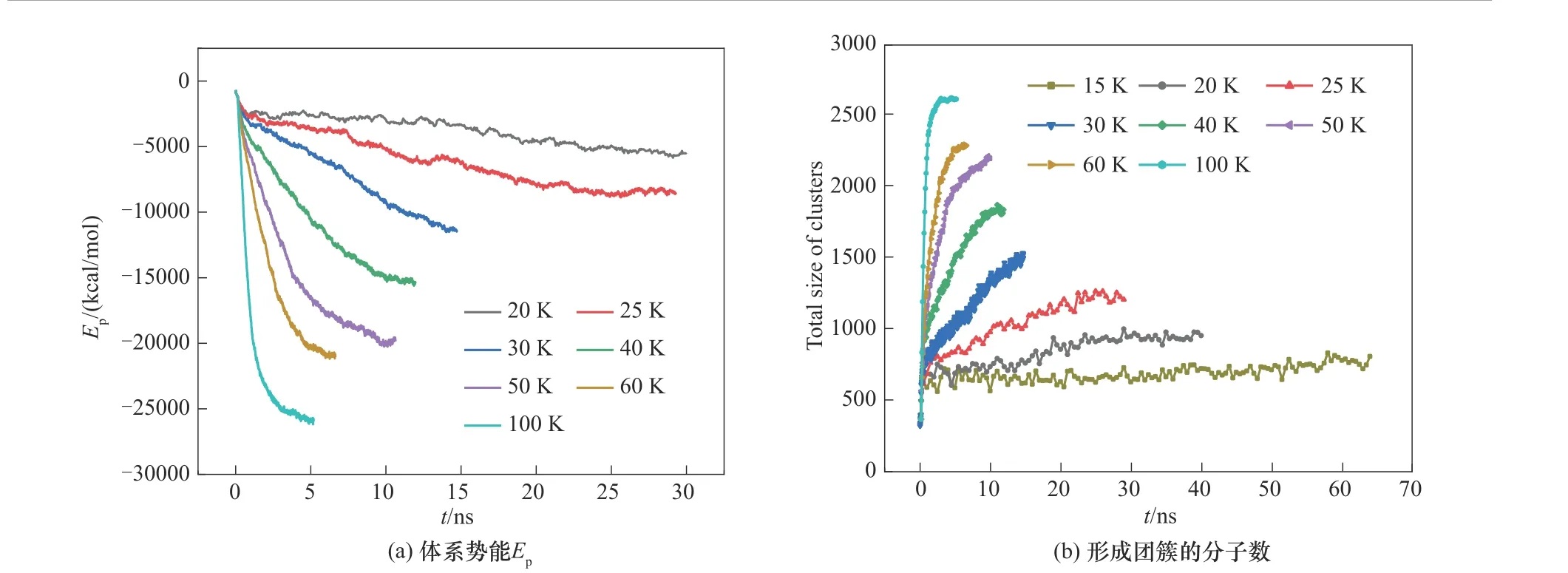
圖4 不同δT體系中水分子的團聚演化Fig.4 Evolution of water molecules aggregation for different δT systems

采用Einstein 法[29]計算擴散系數，通過對粒子所走的路徑進行一段時間的統計，計算得到相應的均方位移（mean square displacement, MSD），然后MSD對時間求導并除以6 得到擴散系數，其具體的計算過程如下：

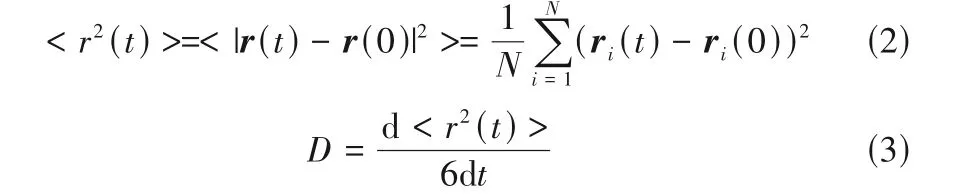
式中，N為系統內總粒子數；ri(t)為第i個粒子在t時刻的位置矢量；D為擴散系數。通過模擬，統計得到MSD 隨時間的變化曲線如圖5 所示，從圖中可以看到，δT越大，相應的擴散系數越小，δT為20、25 K體系的擴散系數相較其他δT更為接近。

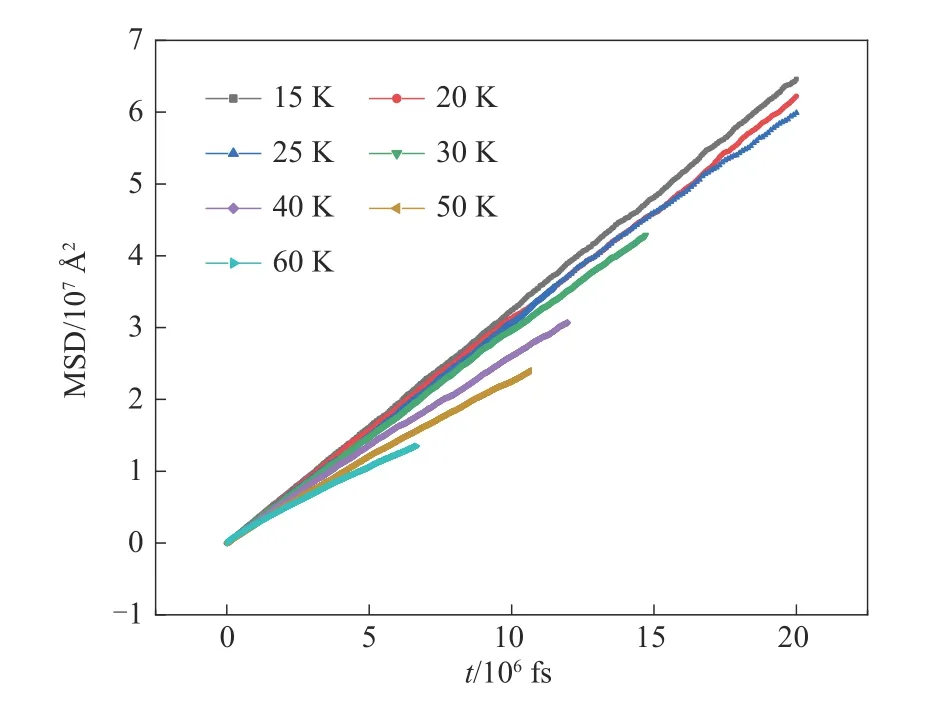
圖5 不同δT體系的均方位移MSD隨時間的變化Fig.5 Variation of mean square displacement with time for different δT systems

在以上對團簇分子數和擴散系數的統計結果的基礎上，為了比較不同δT體系中的團簇分布演化的區別，需要找到某個時間節點或尺寸節點來作為比較基準，這里選取區域分布近平衡的時候，此時對于不同δT體系的“趨于平衡”的趨勢與擴散趨勢這兩趨勢的差值基本保持穩定，其中“趨于平衡”的趨勢利用Boltzmann 分布，根據溫度的分布來計算，擴散趨勢則根據擴散系數來表征，據此經統計得到當最大團簇達到65 時，兩趨勢的差值基本一致，因此比較了最大團簇都為65 時各δT體系中的總團簇分子數以及擴散系數，結果如圖6所示，從中可以看到對于初始飽和溫度為423 K 的純蒸汽冷凝，總團簇分子數和擴散系數均在δT=25 K 處出現一個明顯的轉折點，表明近壁空間溫度從氣相到壁面不是突變的，而是存在過渡的，且這個轉折點正好反映了瑞利散射實驗[17]中近壁平臺區那個轉折點，證實了團簇空間分布中一定存在特征轉折點，由于δT的大小反映團簇尺寸變化的快慢，因此這個轉折點恰恰就是近壁團簇分布的密集區的轉折點，根據圖6 的模擬結果，以轉折點的δT=25 K（Ti=398 K）為界，δT＞25 K 的更靠近壁面的空間區域為團簇稠密分布的近壁區，對應文獻[26]實驗結果中距離壁面600 μm 以內的空間區域，δT＜25 K 的逐漸靠近氣相主體的空間區域為擴散發展過渡區。

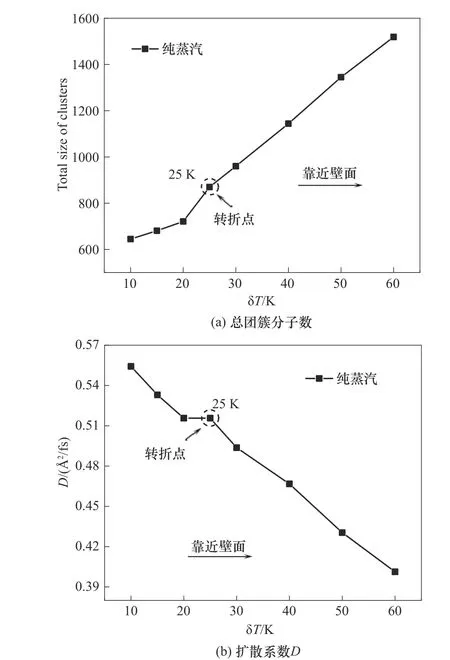
圖6 近壁空間中的團簇分布演化的特點Fig.6 Characteristics of clusters distribution evolution in the near wall region

為了進一步探究近壁空間中團簇分布和過冷度的轉折點的存在以及變化，模擬了不同體相蒸汽壓力下的純蒸汽冷凝過程，包括初始飽和溫度為423 K(0.4760 MPa)，398 K(0.2321 MPa)和373 K(0.1013 MPa)的三個溫度對應的不同壓力體系，模擬結果如圖7 所示，可以看到三個壓力條件下均存在特征轉折點，當水蒸氣的初始飽和溫度降低（壓力降低）時，轉折點對應的δT增大，這說明了團簇尺寸隨著離壁距離快速下降，較大的團簇更靠近壁面，團簇分布的稠密區更薄，此外，還發現降低壓力對靠近壁面和靠近氣相主體區域的團簇的影響相對更大一些，且壓力越低，這種影響越突出。

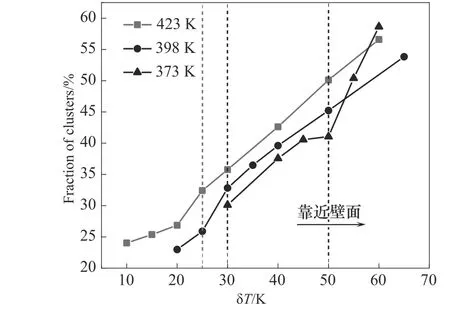
圖7 蒸汽壓力對近壁空間中的團簇分布的影響Fig.7 Effect of vapor pressure on cluster distribution in the near wall region

3.2 不凝氣對近壁空間中團簇分布的影響

由于不凝氣的存在對實際的冷凝過程影響非常大，本文進一步探究了相同初始氣相溫度下含10%氮氣的水蒸氣體系的冷凝過程。N2分子間作用勢使用標準12/6 LJ勢，表達式如下：

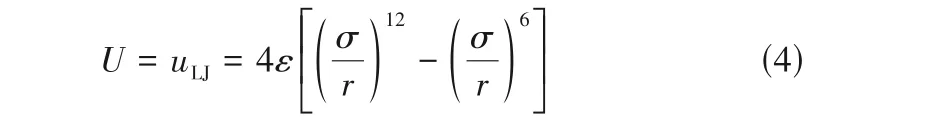
其中，εN-N=0.200527 kcal/mol，σN-N=3.623 ?，根據Lorentz-Berthelot 混合原則[30]有σN-O=(σN-N+σO-O)/2，εN-O=(εN-NεO-O)1/2，計算可得εN-O=0.19271 kcal/mol，σN-O=3.39095 ?。與純蒸汽的模擬過程類似，首先對整個體系進行能量最小化，緊接著對水分子和氮分子分別進行NVT 系綜下的弛豫，控制初始溫度為423 K，模擬150 ps,稍微平衡一下，形成一個該溫度下正常的隨機分布，選用Nose-Hoover 控溫方法進行溫度控制，最后降低不同的溫度δT進行NVT系綜下的模擬直到平衡。使用Ovito、Vmd、Origin 和Matlab 軟件對輸出的結果文件進行數據提取和分析。

與純蒸汽冷凝類似，在氮氣存在的情況下，如圖8(a)所示，體系勢能隨時間不斷減小，并最終達到穩定，且δT越大，即距離過冷壁面越近，體系勢能下降越快。從MSD 隨時間的變化[圖8(b)]中同樣可以看到δT越大，相應的擴散系數越小。通過統計分析“趨于平衡”的趨勢和擴散趨勢兩趨勢的差值，得到對于含10%氮氣的冷凝體系選體系中最大團簇都達到60左右的時刻作為比較基準，進一步統計了相應各δT體系中的總團簇分子數以及擴散系數，結果如圖8(c)、(d)所示，可以看到對于含10%氮氣的水蒸氣冷凝，總團簇分子數和擴散系數均在δT=35 K 處出現特征轉折點，δT＞35 K 對應稠密分布的近壁區，δT＜35 K為擴散發展過渡區。

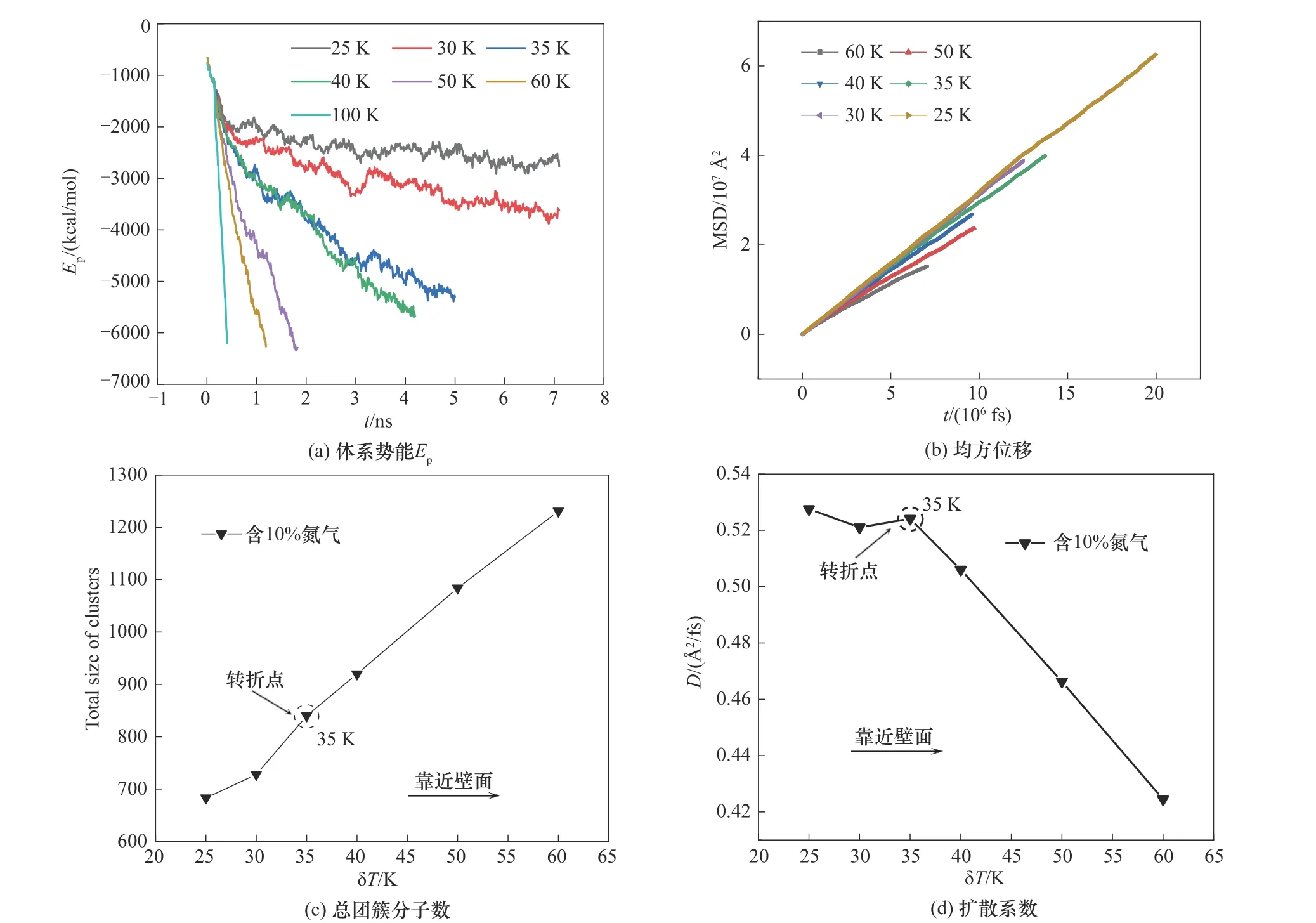
圖8 氮氣存在下近壁空間中水分子的團聚演化與團簇分布特點Fig.8 Evolution of water molecules aggregation and characteristics of clusters distribution in the near wall region with nitrogen

為了探究不凝氣對轉折點的影響，在添加10%氮氣的基礎上，繼續增加氮氣含量至20%，比較純蒸汽和不同氮氣含量下的團簇的分布演化，結果如圖9 所示，發現純蒸汽冷凝的近壁空間分布的轉折點（δT=25 K）小于含10%不凝氣（δT=35 K）和含20%不凝氣（δT=45 K）冷凝的轉折點，并且不凝氣含量增加時，轉折點δT值增大，說明純蒸汽冷凝的轉折點更靠近氣相主體，也就是說純蒸汽冷凝的團簇分布的稠密區更厚一些，而不凝氣的存在使得擴散區變大，所以當體系含不凝氣時，要達到與純蒸汽條件相似厚度的稠密區，需要更高過冷。

圖9 不凝氣對近壁空間中的團簇分布的影響Fig.9 Effect of noncondensable gas on cluster distribution in the near wall region

依據本文分析，蒸汽壓力或不凝氣含量等工藝參數將影響近壁團簇密集區的厚度，以至于最終影響冷凝效果。這個結果從一個新的角度揭示了目前一些冷凝強化效果的微觀機理，例如提高過冷度的根本原因在于增加了團簇稠密區的厚度。在冷凝過程的強化結構設計上，也提出了新的設想，即不僅是壁面上的強化結構，強化結構可以拓展到近壁區的空間中去。從這個角度可以借鑒仙人掌刺、沙漠甲蟲背部凸起、葉片表面纖毛等生物具有的用于集水的表面化學組成和特征高度結構[31-35]，說明可以通過在空間中加入固相介質來捕獲氣相團簇；強化結構還可以將團簇盡量控制在稠密區內，減少團簇向外擴散逃逸；甚至還可以通過特定的表面化學成分來限制氮氣的運動，從而讓水分子獲得更大碰撞概率。總之，本文關于近壁團簇分布規律和機理的新發現對實際工程中有冷凝調控需求的表面的設計具有特殊的指導意義。

4 結 論

結合近壁團簇分布實驗結果所構建的凝結過程近壁物理圖景[17,26]，以唯象和抽樣分析的手段，利用分子動力學模擬研究了冷凝過程近壁幾百微米空間中的溫度變化規律與團簇演化機制，得到以下結論。

（1）在壁面過冷的凝結過程中，近壁區介質溫度并非突變，存在一個特征轉折點。以總過冷度100 K 為例，該轉折點約處于δT=25 K，并將近壁團簇分布分為靠近過冷壁面的團簇稠密區（δT＞25 K）和靠近蒸汽體相的擴散發展區（δT＜25 K）。稠密區對應文獻實驗中團簇尺寸變化劇烈的區域。

（2）純蒸汽凝結過程，體相蒸汽壓力降低，特征轉折點對應的過冷度δT增大，這說明了團簇尺寸隨著離壁距離快速下降，反映了團簇稠密區厚度更薄。即低壓條件，較大團簇更靠近壁面，壁面微結構對成核凝結過程的調控更重要。

（3）不凝性氣體存在時，雖然特征轉折點δT值較純蒸汽條件時大，表明了較大團簇更靠近壁面，但同時空間中團簇分布的擴散區也變寬。這表明要達到與純蒸汽條件相似厚度的稠密區，需要更高過冷度，另外還可通過一定手段捕獲或限制擴散區逃逸的團簇。

（4）根據近壁團簇演化的分區特性，成核冷凝過程的調控，不僅可以考慮壁面微納功能結構的設計，還可考慮通過近壁幾百微米空間中的材料和結構的設計，更多地捕獲稠密區內團簇或避免團簇向外擴散，以及團簇稠密區與擴散區的調控等。