PID控制器最優參數整定方法的研究

劉冰琪 解 初 劉 鵬

1.泰山科技學院 山東泰安 271000；2.國網山東省電力公司泰安供電公司 山東泰安 271000

目前工業自動化水平已經成為衡量各行各業現代化水平的一個重要標志。同時，控制理論[1]的發展也經歷了古典控制理論、現代控制理論和智能控制理論三個階段。一個閉環控制系統[2]由控制器、執行器、被控對象、測量變送器以及輸入輸出接口組成，其中最核心的是控制器部分。目前，PID控制器多種多樣，學術界及各大企業也基于人工智能算法紛紛開發了智能控制器。但在實際工業中，應用最廣泛、最基礎的依然是簡單控制系統，該系統所應用的PID控制器通過經典的PID整定方法加現場調試來確定其參數，以達到較好的控制效果。因此，本文基于閉環控制系統確定PID控制器的最優參數整定方法。首先，基于MATLAB/Simulink搭建閉環控制系統模型，然后基于現有的PID參數整定方法確定PID控制器的參數，最后基于控制系統的動態性能評價指標給出最優參數整定方法，并驗證了該方法的有效性。

1 閉環控制系統模型搭建

閉環控制系統正常運行情況下，過程輸出信號y(t)的變化會引起控制信號u(t)的響應，合理可靠的PID控制器能夠使得控制信號u(t)準確迅速地響應過程輸出信號y(t)的變化，從而實現控制效果，以獲得預期的系統性能。

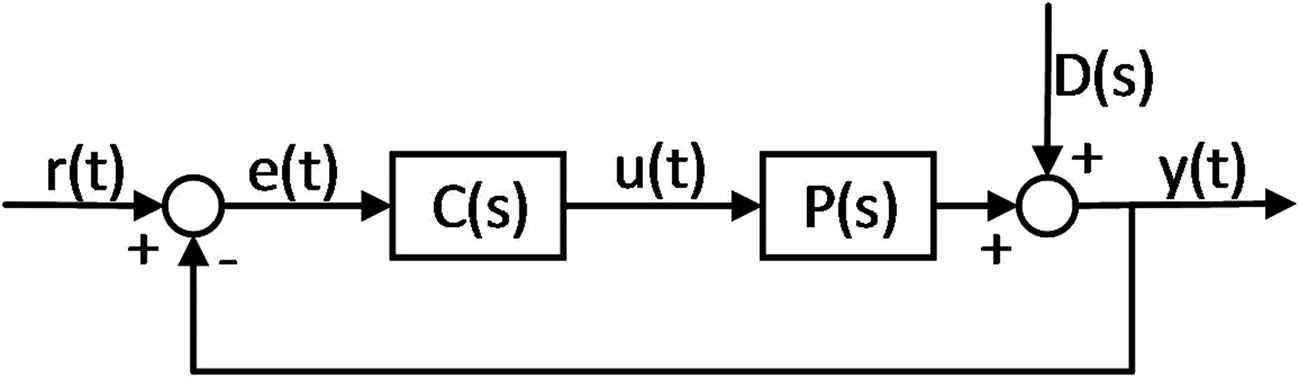
圖1 閉環控制系統結構框圖

本文根據圖1所示閉環控制系統結構框圖，利用MATLAB/Simulink搭建閉環控制系統仿真模型，并給定被控對象的傳遞函數：

(1)

2 PID參數整定方法

PID控制器是常規控制器中性能最好的一種。由于它具有各類控制器的優點，因而使系統具有更高的控制質量，其傳遞函數為：

(2)

控制器參數整定[3]是指通過設定控制器的可調參數，使輸入特性和響應特性獲得最佳匹配，以改善系統的動態和穩態性能，取得最佳的控制效果。對于PID控制器來說，可調參數包括比例增益Kc、積分時間Ti和微分時間Td。PID參數整定方法可以分為解析式方法、啟發探索式方法、頻率響應法、最優化方法以及自適應整定法。

啟發探索式參數整定方法是由動手實踐發展起來的，具有較強的廣泛性和適用性，本文在現有研究的基礎上對該方法進行深入研究，并基于閉環控制系統確定PID控制器的最優參數整定方法。

(一)地區間過度競爭產生的負面效應

2.1 穩定邊界法

設積分時間Ti=∞，微分時間Td=0，使控制器工作在純比例情況下，設置比例增益由小逐漸變大，使系統的輸出響應呈現等幅振蕩。

根據閉環控制系統模型，在沒有積分和微分作用的情況下，將系統投入閉環自動運行，逐漸增大比例增益Kc，直到系統響應為等幅振蕩的狀態，此時比例增益Kc即為臨界比例增益Km，對應的振蕩周期即為臨界振蕩周期Tm，記錄Km、Tm，即：

Km=1.387Tm=30s

(3)

基于穩定邊界法[4]PID參數整定的經驗算式，求取控制器的整定參數，該整定方法是以得到4∶1衰減曲線為目標。根據公式(3)，運用經驗公式計算得到PID控制器參數：

Kc=0.6Km=0.8322

Ti=0.5Tm=15s

Td=0.125Tm=3.75s

(4)

根據公式(4)所得結果設定閉環控制系統仿真模型中PID控制器的參數，得到穩定邊界法響應曲線如圖2所示。

穩定邊界法應用簡單便捷，但該方法存在使用局限：從工藝上看，首先算法要求被控變量能夠承受等幅振蕩的波動；其次要求被控對象應為二階和二階以上或具有純滯后的一階以上環節，否則在純比例環節控制下，系統無法出現等幅振蕩狀態，即無法獲取PID控制器參數整定結果。

2.2 衰減曲線法

閉環控制系統中，在純比例控制器作用下由大到小不斷調節比例增益Kc，并添加階躍擾動信號觀察輸出響應的衰減過程，直至出現4∶1衰減響應曲線[5]。此時比例增益Kc稱為4∶1衰減比例增益，用Ks表示，相鄰兩波峰間的距離稱為4∶1衰減周期Ts。根據閉環控制系統模型，不斷調整比例增益Kc，直到獲取4∶1衰減響應曲線，此時：

Ks=0.7Ts=34.63s

(5)

根據公式(5)所得Ks和Ts，運用衰減曲線法PID參數整定的經驗公式計算控制器整定的參數值，即：

Kc=0.8Ks=0.56

Ti=0.3Ts=10.92s

Td=0.1Ts=3.64s

(6)

根據公式(6)所示結果設定閉環控制系統仿真模型中PID控制器的參數，得到衰減曲線法響應曲線如圖2所示。

2.3 科恩-庫恩反應曲線法

反應曲線法對比值τ/T較為敏感，科恩-庫恩基于相同模型進行深入研究，給出了與比值τ/T具有一定相關性的另外一組整定公式，整定公式如表1所示，稱為科恩-庫恩反應曲線法[6](簡稱CC方法)，該公式對于不同的τ/T比值，具有較好的一致性。

表1 科恩-庫恩反應曲線法PID控制器參數

根據公式(1)可知被控對象增益K、時間常數T及滯后時間τ，即：

K=3 T=16 τ=9

(7)

將公式(7)所示結果代入表1所示科恩-庫恩反應曲線法得到PID控制器整定參數Kc、Ti、Td，即：

Kc=0.8735Ti=18.2sTd=2.969s

(8)

根據公式(8)所示結果設定閉環控制系統仿真模型中PID控制器的參數，得到科恩-庫恩反應曲線法響應曲線如圖2所示。

2.4 現場試湊法

試湊法是根據系統響應情況不斷調整PID控制器參數的方法。此方法在觀察響應曲線的同時不斷調整PID控制器的參數，直到獲得滿意的控制效果為止。

通常來講，增大比例增益Kc會加快系統的響應速度，提高系統的快速性，但過大的比例增益會使系統超調過大，甚至產生振蕩導致系統穩定性降低，并且過大的比例增益可能導致系統存在較大的誤差。減小積分時間Ti使得積分作用增強，系統的靜差減小，并且有利于縮短系統消除靜差所需的時間，但過大的積分時間，會導致超調變大，使系統的穩定性降低。增加微分時間Td使得系統的響應速度加快，響應提前，進而減少超調，但會導致系統抑制干擾的能力變差，另外整定不當反而會使系統處于不穩定狀態。因此，試湊時一般根據比例增益Kc、積分時間Ti和微分時間Td參數的特點，對系統可調參數實施先比例、后積分、再微分的整定步驟。

2.4.1 比例部分整定

設置積分時間Ti為無窮大，微分時間Td為零，將積分和微分作用消除，使系統在純比例控制器下運行。調整比例增益Kc使其由小到大變化，并觀察系統的響應情況，直至響應速度較快且有一定范圍的超調為止。

2.4.2 積分部分整定

純比例控制系統無法實現零靜差調節，因此需加入積分環節的作用。在整定時將積分時間Ti由大逐漸減小，觀察系統過程輸出信號的變化，直到實現無差調節。此時超調量在原有基礎增大,因此，需適當降低比例增益Kc。

2.4.3 微分部分整定

若系統經比例積分環節調節后仍無法取得滿意的響應結果，此時應添加微分環節。整定時先將微分時間Td從小逐漸增加，觀察系統的超調量和穩定性。同時相應地微調比例增益Kc及積分時間Ti，直到系統調節的靜差和響應速度滿足控制要求。

根據上述現場試湊法的參數整定過程，調整閉環控制系統中PID控制器參數，當比例增益Kc、積分時間Ti和微分時間Td為公式(9)所示結果時，系統響應結果最佳，得到現場試湊法響應曲線如圖2所示。

Kc=0.55 Ti=22s Td=3s

(9)

3 動態性能指標

動態性能指標是衡量閉環控制系統性能優劣的重要指標，動態性能指標包括上升時間、峰值時間、調節時間、超調量等。其中上升時間tr指響應從零第一次上升到終值所需要的時間。峰值時間tp指響應超過其終值到達第一個峰值所需要的時間。調節時間ts指響應到達并保持在終值±5%或±2%誤差內的最短時間。超調量σ%指響應的最大偏移量y(tp)與終值y(∞)的差σp，再與終值y(∞)相除的百分數。即：

(10)

衰減比是指兩個連續的最大誤差之比。穩態誤差為系統穩態值與輸入設定值之差。

根據閉環控制系統的動態性能指標對上述PID控制器參數整定響應結果進行對比分析，不同參數整定方法而得到的系統響應曲線如圖2所示。

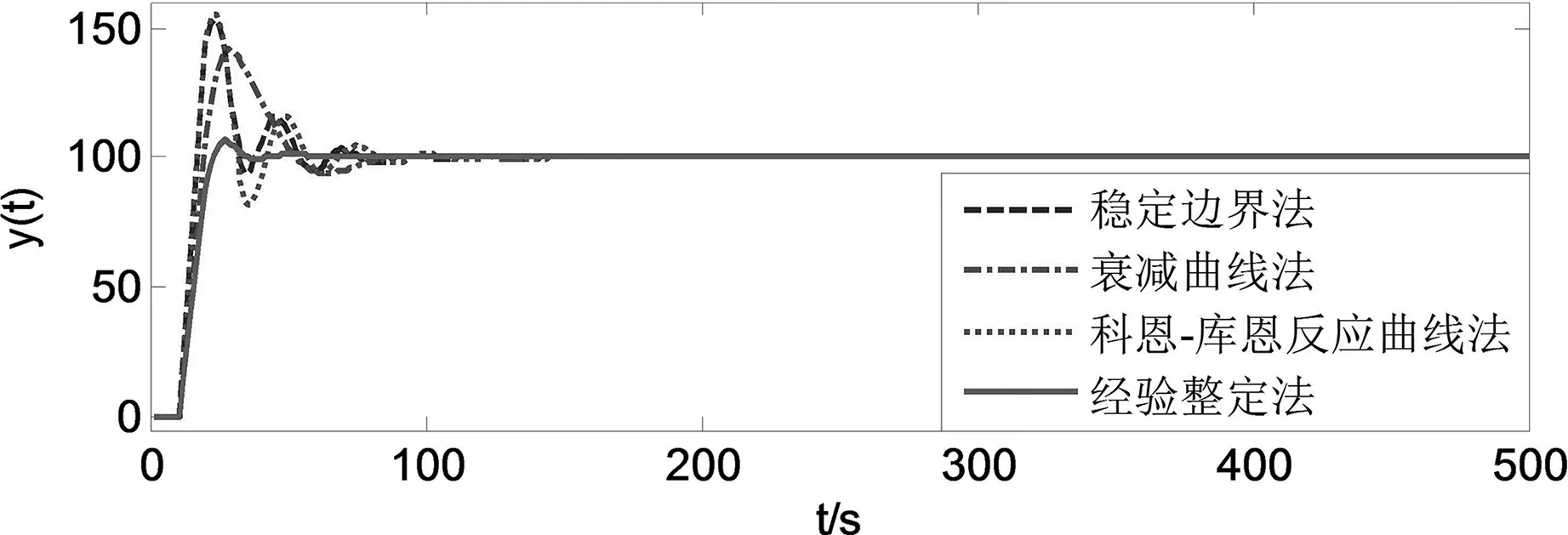
圖2 最優參數整定方法響應曲線對比圖

基于控制系統的動態性能指標分析四種參數整定方法的響應曲線可得表2所示結果：采用穩定邊界法與科恩-庫恩反應曲線法得到的PID閉環響應曲線基本一致，相比之下穩定邊界法較科恩-庫恩反應曲線法超調量小，穩定性高。衰減曲線法得到的PID閉環響應曲線與穩定邊界法、科恩-庫恩反應曲線法相比延遲及峰值響應時間增大，但系統的振蕩程度減小。而現場試湊法得到的PID響應曲線與其他三種整定方法相比，上升時間及峰值時間略大，但系統達到穩定所需時間更短、系統超調量更小，穩定性更高。因此，現場試湊法性能優于其他三種方法。

表2 不同參數整定方法下的動態性能指標

4 結論

本文在現有研究基礎上基于閉環控制系統對穩定邊界法、衰減曲線法、科恩-庫恩反應曲線法及現場試湊法四種主要的參數整定方法進行對比分析，并基于分析結果確定PID控制器的最優參數整定方法。現場試湊法性能優于其他三種方法,但在實際的生產中，現場試湊法可能需要較長的試湊時間，因此可以先根據衰減曲線法預先確定PID控制器參數作為參照，然后根據現場經驗調整控制器的控制效果，以獲得預期的系統性能。