黃土地區某鐵路專用線路基動力響應規律

交通強國戰略的提出再次肯定了交通運輸在國民經濟發展中的重要驅動作用.鐵路運輸以其運量大、速度較快等特點在公共交通領域備受重視.長期以來，從業人員一直致力于改善路基服役性能，提升鐵路運輸的社會經濟效益.列車運行荷載下路基動力響應研究涉及附加動應力分布及地表環境振動兩方面主要內容，是路基工程設計、施工和減隔振的重要參考.

移動列車荷載引起的附加動應力分布規律是路基工程領域的重點關注內容.大量的現場測試、模型試驗和數值模擬研究均表明：列車荷載作用下，路基內部動應力沿深度迅速衰減，動應力幅值隨車速的提高而增大.相關研究結論是確定路基結構層厚度和填筑參數的主要依據.為了方便工程應用，《鐵路路基設計規范》TB 10001—2016建議采用 Boussinesq 公式獲取列車運行荷載下路基內部動應力分布，采用與車速相關的放大系數近似考慮荷載移動效果的影響.文獻[6]考慮各結構層彈模對動應力分布的影響，采用Odemark理論計算路基內部動應力分布規律.

目前主流的兩種動應力影響深度界定標準分別是“動應力幅值衰減至最大幅值的10%時對應的深度”和“動應力幅值沿深度分布曲線與1/10或1/5自重應力線交點的深度”.由于圍壓是影響路基土體力學和強度參數的重要因素，一般推薦采用動應力幅值曲線與自重應力線交點確定動應力影響深度.總體而言，附加動應力分布受路基土質條件、道床結構、車速和軸重等多重因素影響，衰減曲線大同小異，動應力影響深度普遍在3～6 m范圍內.

目前的大量研究習慣針對具體工程背景評估列車運行誘發的環境振動對周邊敏感建筑或區域的影響.孟慶成等基于現場測試和數值模擬評估了某火車站高架候車廳結構車致振動特性及振動對舒適度的影響.Yang等采用2.5D有限元方法研究了高速列車運行情況下空溝的隔振效果.Thompson等通過2.5D有限元方法研究了路基內部橫向波阻塊的減振效果及機制.Coulier等以西班牙El Realengo地區某鐵路沿線場地為背景研究了混凝土灌注樁擋墻對地表環境振動的隔振效果.此外，Dijckmans等以瑞典Furet地區某鐵路沿線場地為背景研究了波紋板樁板墻的隔振效果.Yarmohammadi等結合列車荷載激發環境振動的特點發展了一種耦合方法，研究指出雙隔振溝的減振效果比單溝更好.馬骙骙等通過開展寶蘭高鐵路塹段地面垂向振動現場測試研究了高速列車荷載下路塹的地面垂向振動隨距離傳播規律，指出場地速度特性(地基覆蓋層與下臥層模量比、覆蓋層厚度)是影響地面振動劇烈程度的重要因素.相比于動應力分布規律，環境振動研究涉及振動理論知識、情況各異的路基斷面甚至精細化的地基-建筑物基礎相互作用等問題，因此獲得的量化成果相對較少.

在眾多的鐵路路基動力響應研究手段中，2.5D有限元方法因具備計算效率高、對復雜斷面適應性好及理論基礎完備等優點，在計算列車運行情況下路基動力響應方面獨具優勢.近年來其適用范圍及應用場景不斷擴展，在復雜路基環境振動規律、多相介質地基動力響應、路基臨界速度預測等方面的應用屢見不鮮.

在高速鐵路大量修建的政策背景下，鐵路路基動力響應研究大多集中在我國東南沿海軟土地區，黃土地區相關研究的系統性和深度均有所欠缺.由于黃土地區溝壑縱橫，修筑鐵路線路時大量采用填土路堤結構.闡述列車運行荷載引發的路堤-地基系統響應規律是細化設計參數、評估服役性能的重要舉措.

徐州傳統地方戲曲梆子戲在2008年被列為國家級非物質文化遺產，江蘇梆子劇院有限公司（前身江蘇省梆子劇團），現已實行企業化管理。梆子戲在徐州、河北地區目前仍繼續上演，有一批固定觀眾。

本文依托某鐵路專用線工程，旨在通過現場測試和2.5D有限元模擬揭示新建貨運線路和臨近既有客運線列車運行情況下路基動力響應規律，評估貨運列車運行情況下路基動應力分布及影響深度，討論線路附近辦公區域的環境振動規律.以2.5D有限元為主要研究手段，輔以現場實測數據，在驗證數值模擬精度的前提下開展參數分析.

1 現場測試概況

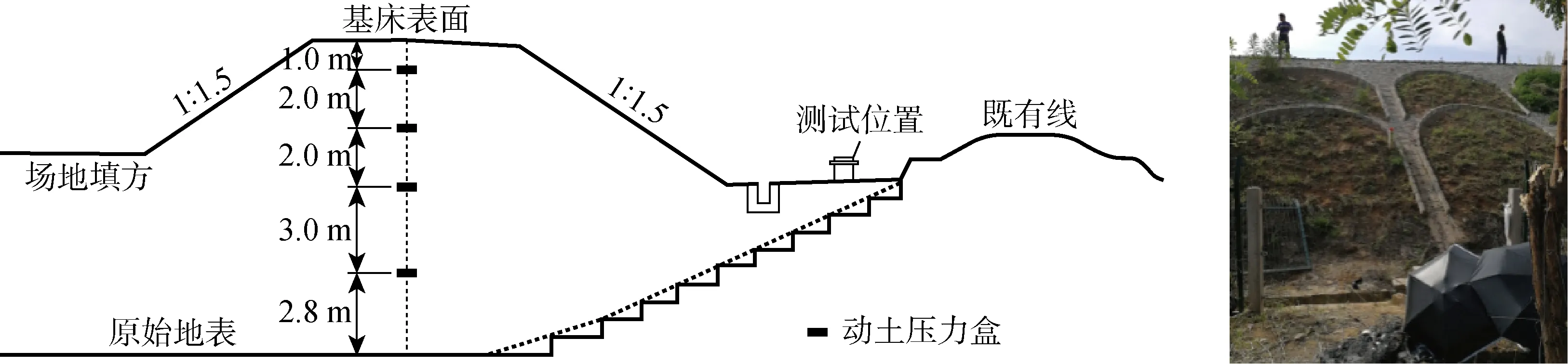
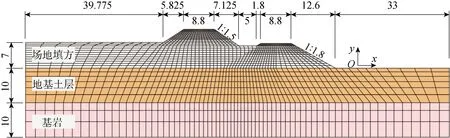
依托陜北黃土梁峁溝壑區某鐵路專用線工程開展，測試斷面位于洛河一級階地，原始地基未經強夯處理.地層由上向下依次為黏質黃土(Ⅰ級非自重濕陷性黃土)及下覆基巖(頁巖夾砂巖).黃土覆蓋層厚度約10.0 m，地層分布較均勻，起伏變化較小.路堤中心填高10.8 m，邊坡坡率1∶1.5.地下水位標高在路堤底面下部5 m處，年變化幅度在2 m左右.路堤主體采用壓實黃土填筑，與既有線采用臺階搭接.

考慮到減少模板間的縫隙面，保證模板整體結構的穩定性，并盡量減小滲透。大壩上游背水面對應的模板規格為3m（寬）×3.5m（高），其中每三塊模板組成一套。大壩下游的背水面對應的模板規格則為邊長2.5m的正方形結構，從而形成雙層翻升模板。基于提升模板剛度的目的，可以在模板頂面邊緣部分增設修飾角鋼護面。

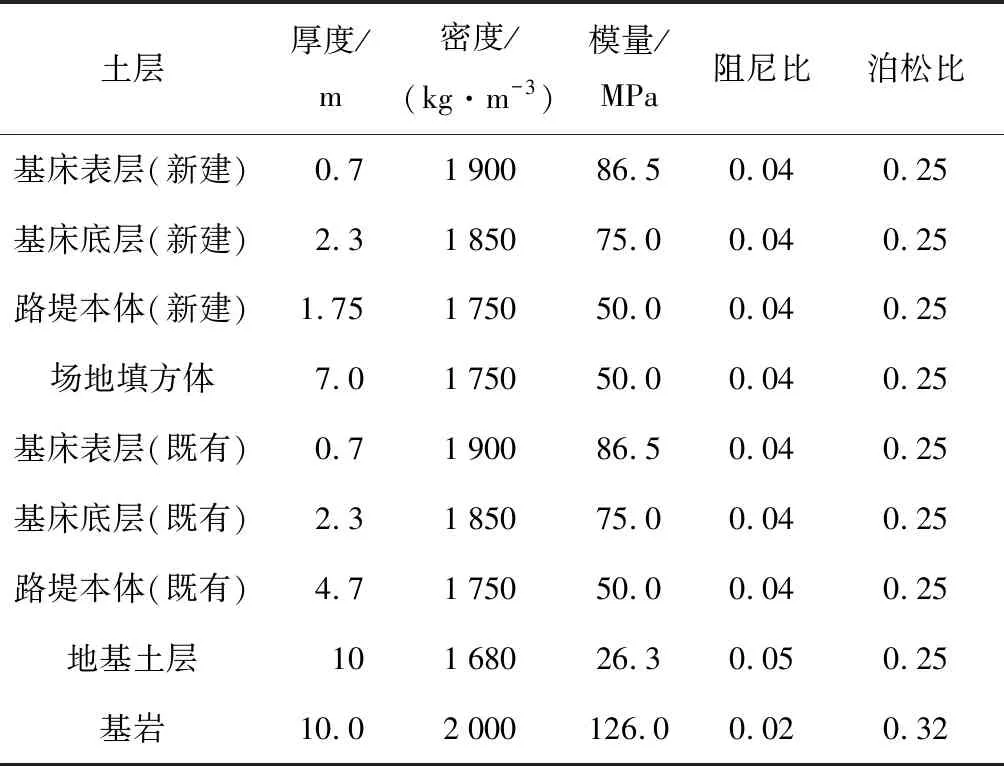
以圖1現場測試斷面為原型建立2.5D有限元模型，如圖4所示.土體參數參照前期開展的相同工程背景下壓實黃土動力參數研究及其他相似工程背景下的研究成果，如表1所示.需要指出的是，由于年代久遠，既有線路堤設計參數無從考證，其分層情況及土體參數參照新建路堤設置.參照文獻[20, 24]，有砟軌道系統(道砟-枕木-緊固件-鐵軌)等效為坐落在基床表層的歐拉梁，抗彎剛度=13.254 MN·m，單位長度質量=540 kg/m. 列車軸重及運行速度與現場測試一致.

..軌道系統動力方程 將軌道系統模擬為歐拉梁，輪軸荷載作用下變換域內軌道的振動變形可以描述為

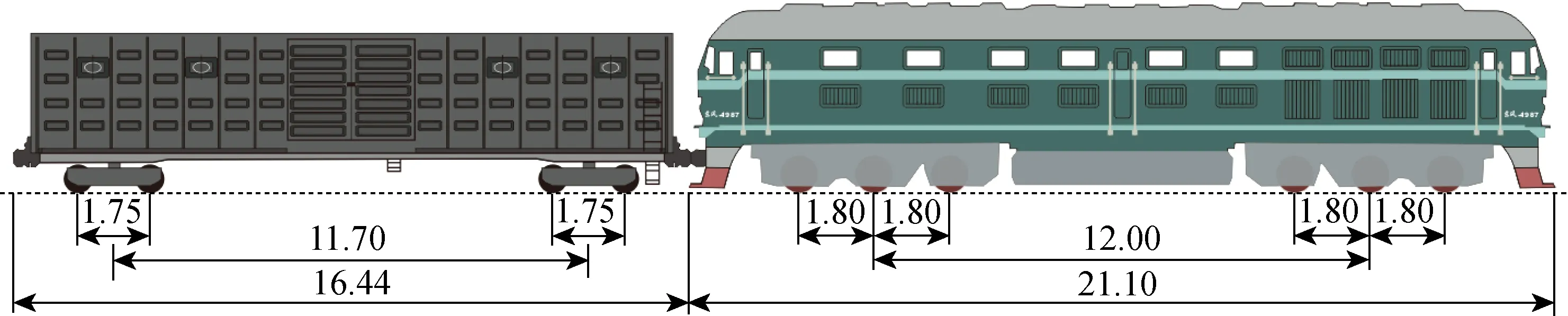
測試采用BY-1型電阻式雙油腔動土壓力盒，盤面尺寸20 cm，量程0.4 MPa.土壓力盒盤面較薄，遇尖銳物體易損壞，因此并未在道床底面及基床表層范圍內布設.數采儀器型號為DH5922N，采樣頻率 1 000 Hz.測試重載列車由1節車頭及10節滿載棚車組成，如圖2所示.車頭為東風4B型貨運內燃機車，軸重23 t；棚車為P64K型，滿載軸重為 22.5 t，測試車速30 km/h.

2 2.5D有限元模型驗證及優化

2.1 2.5D有限元簡介

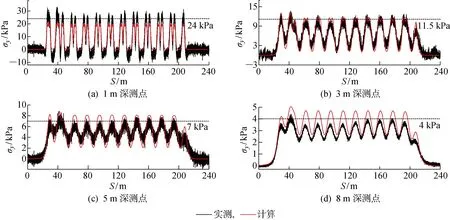
列車運行荷載下圖1中的4個測點處豎向動應力的變化規律如圖5所示，圖中=為空間長度.通過對比數值模擬結果和現場測試數據可知，二者波形一致，幅值近似.進一步從路基動應力響應角度驗證了本文2.5D數值模擬方法在模擬列車運行情況下路基系統動力響應的可行性.

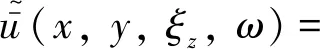
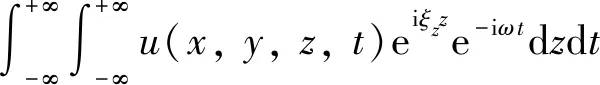
(1)

式中：為位移；為波數；為圓頻率；i為虛數單位；上標“-”和“～”分別代表波數和頻率變換.

..列車荷載 三維空間中沿軸移動的荷載可以表示為

設計方面的因素。主要有設計水平的高低、圖紙質量的好壞等，具體表現為工程設計采用不成熟的技術方案，設計錯誤、遺漏或缺陷，圖紙供應不及時、不配套或出錯等。

“我壓根兒沒想到張仲平會當真。”左達說，“為了拿到這幢樓的拍賣推薦函，不下十家拍賣公司找過我，我跟他們開了同樣的條件，你們公司是唯一當真的。”

(,,,)=(,)(-)()

(2)

式中：函數(,)表示荷載在與軸垂直斷面上的分布特征；函數(-)表示荷載的移動特征，為荷載的移動速度；函數()表示荷載的時變特征.本文列車荷載在變換域中的表達式參照文獻[20].

..地基系統動力方程 系統在變換域中的動力方程可表達為

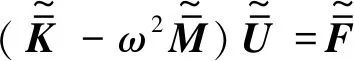
(3)

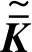
見面第一句話，他就對睜著一雙疑慮大眼睛的女主人說，我有一個朋友叫老林，今晚我和他在一起。你放心吧，不會有事。我們說好的，互相幫忙。

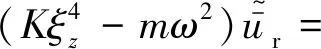
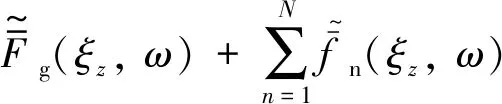
(4)

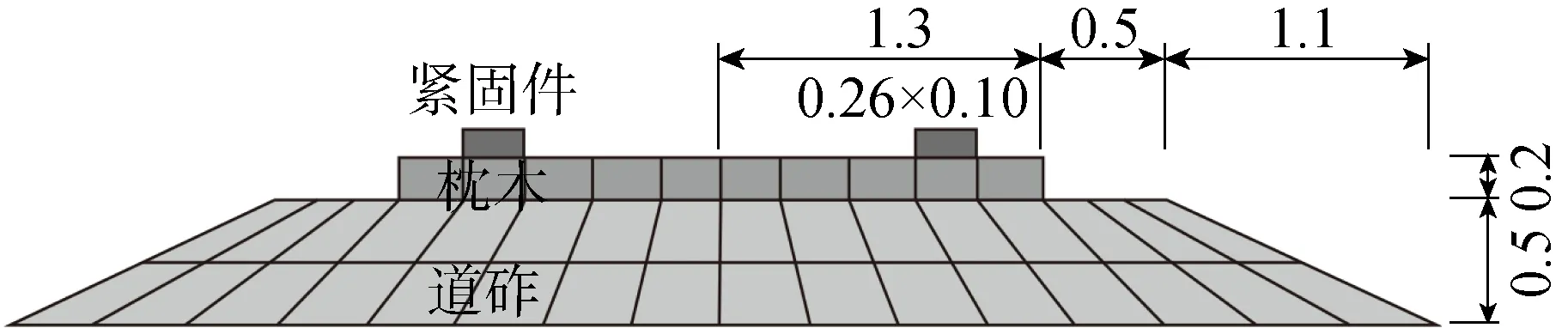
..道砟枕木緊固件各向異性單元建模信息 采用2.5D有限元方法計算有砟軌道路基動力響應時，習慣將道砟-枕木-緊固件-軌道系統等效為坐落在基床頂面的歐拉梁，在歐拉梁上作用沿橫向均勻分布的列車荷載.采用歐拉梁等效時忽略了緊固件豎向剛度、枕木橫向抗彎剛度和道砟體厚度等對荷載傳遞的影響.為了體現上述影響，已有文獻通過各向異性單元考慮了緊固件和枕木對荷載豎向傳遞和橫向分布的影響，但未考慮道砟各向異性的影響.本文建立圖6所示道砟-枕木-緊固件各向異性實體單元，分析軌道系統建模方式對路基動力響應的影響.

在育肥豬日糧中組合使用益生菌與中藥提取物復合物替代抗生素，提高生長性能效果顯著，降低育肥豬背膘厚和提高瘦肉率，效果優于金霉素。

2.2 程序驗證

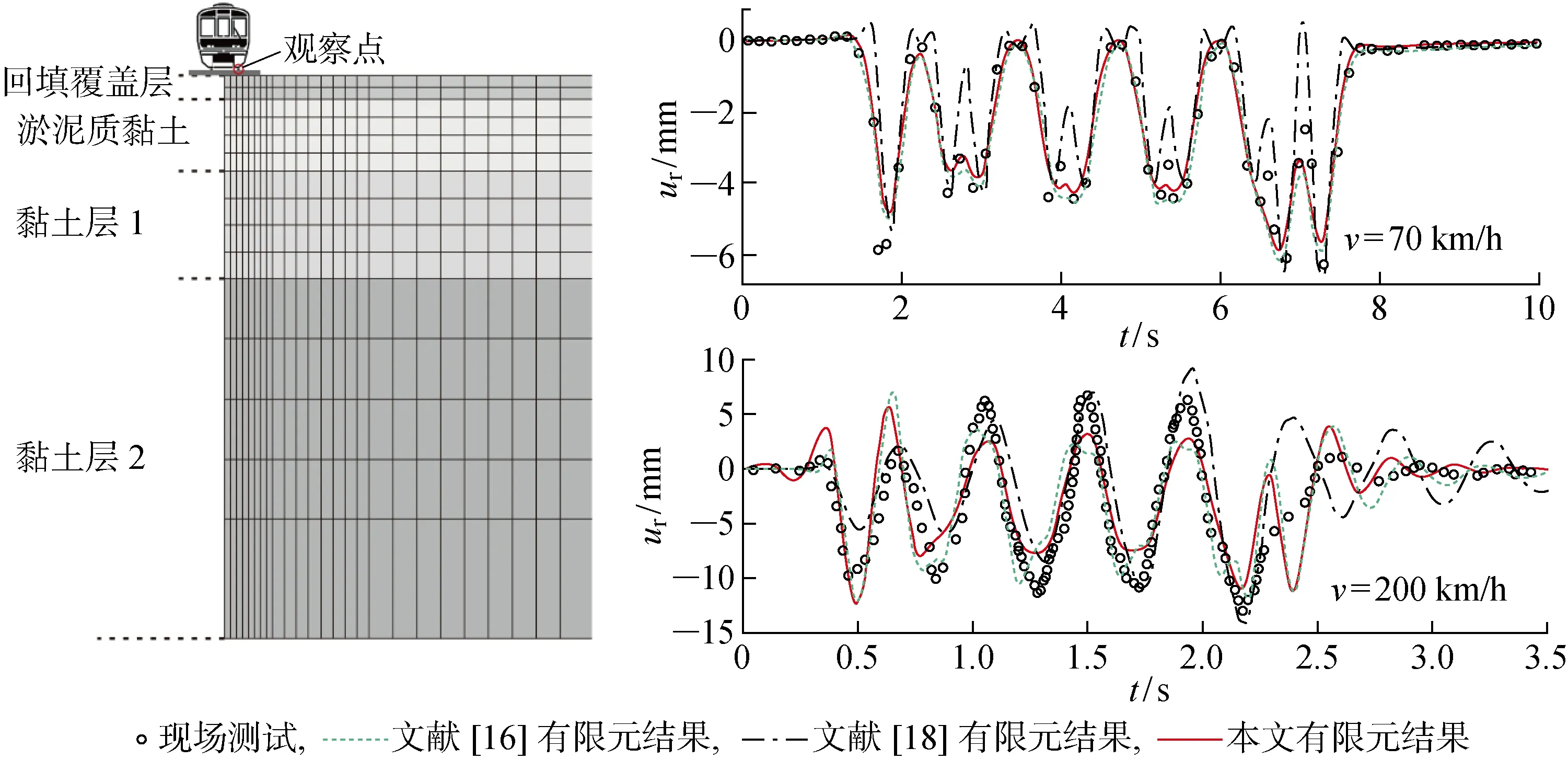
采用MATLAB軟件自編了2.5D有限元計算程序，為了驗證其模擬效果，以瑞典國家鐵路局(BANVERKET)在瑞典西海岸Ledsgard地區進行的X2000型列車運行現場實測數據為參照，通過本文2.5D有限元程序重現了兩種車速情況下軌道位移隨時間的變化規律.網格劃分、地基分層及數據對比如圖3所示.模型采用黏彈性人工邊界作為吸收邊界.可以看出，本文2.5D有限元程序可以較好地模擬列車運行情況下地基系統動力響應規律.限于篇幅， 列車、軌道系統及路基土體參數詳見文獻[16,18].

2.3 現場測試規律的數值重現

根據路堤填筑高程分層多次埋設土壓力傳感器，待路堤填筑完成且變形穩定后開展現場測試工作.路基斷面輪廓、傳感器分布及現場測試情況如圖1所示.根據動應力分布規律及影響深度，在路堤中線處埋設4層土壓力盒，最大埋深8 m.

從桌子上跳下來當然危險，但你阻止了他，他背著你跳，那更危險。所以該有個“訓練策略”。把墊褥鋪在地上，示范從椅子上跳下時身體應該保持怎樣的姿勢、兩腿如何彎曲，起跳后身體、雙腿和雙手怎樣配合行動，著地時身體、雙腿和雙手做怎樣的動作。

2.5D有限元計算方法是基于路基斷面(位于-平面)在列車運行方向保持不變的基本假定建立的.計算時首先采用雙重傅里葉變換得到斷面各節點在頻率-波數域內的響應，然后由傅里葉反變換獲得系統的實際響應.沿列車運行方向和時間的傅里葉變換可以表示為

即便如此，對比響應幅值隨深度的變化規律可以看出，有限元計算獲得的幅值衰減速度比現場測試數據慢.在2.5D數值模擬方面，目前針對其精度影響因素的爭論主要集中在軌道系統抽象的合理性、路基土體的非線性及輪-軌相互作用等方面.在重現路基實際響應規律時，土體動力參數的代表性也會影響預測效果.相關研究指出，交通荷載作用下土體動力蠕變會帶來額外的能量消耗.本文有意依據本次現場實測數據開展進一步研究，分析軌道系統建模方式和土體動力蠕變對路基動力響應的影響.相關研究指出，交通荷載下壓實黃土的動應力-應變關系在一定起始應力范圍內的非線性表現不明顯.結合列車運行情況下路基內部動應力幅值分布情況，暫不考慮土體非線性的影響.

2.4 軌道系統各向異性實體建模對模擬結果的影響

文獻[22]研究了交通荷載下路基填土的動力特性，從動力蠕變角度對土體的滯回特性進行了修正.研究指出土體動力蠕變會額外消耗能量，單個滯回中動力蠕變消耗的能量約等于塑性應變與靜偏應力的乘積，如圖10所示.圖中：為應力，為應變，Δ為循環塑性應變.相比于塑性變形，單元的耗能特性是影響系統動力響應的直接因素，在動力數值分析中可通過調整阻尼比實現.因此，本文嘗試通過提高單元阻尼比的方式間接討論土體動力蠕變產生的額外能耗對路基動力響應的影響.軌道系統采用實體建模.

,rp=()

(5)

式中：為緊固件豎向剛度(取值為1.75×10N/m)；和分別為單元寬度和高度；為枕木間距(取0.6 m).

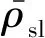
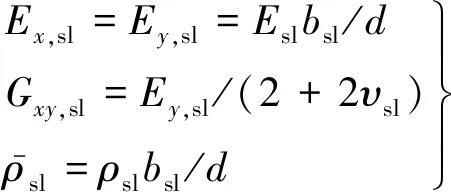
(6)

式中：為枕木混凝土彈性模量(為 12 500 MPa)；為枕木平均寬度(為0.25 m)；為材料密度(為 2 500 kg/m)；為材料泊松比(為0.2).

文獻[26]基于大型三軸試驗設備開展了道砟材料各向異性參數的試驗.依據循環加載試驗結果，道砟材料的9個各向異性參數取值分別為彈性模量,b=900 MPa，,b=,b=600 MPa；泊松比,b=0.31，,b=0.32，,b=0.28；切變模量,b=(,b+,b)/(2+2,b)=572 MPa，,b=(,b+,b)/(2+2,b)=455 MPa，,b=(,b+,b)/(2+2,b)=586 MPa.密度=1 900 kg/m，阻尼比=0.2.

..路基響應規律 分別提取圖1所示測點動應力時程曲線(見圖7)、動應力幅值橫向分布(見圖8)及豎向衰減規律(見圖9)，討論軌道系統建模方式對路基動力響應的影響.圖中：為橫向位置；為豎向深度；,amp為豎向動應力幅值.對比測點動應力時程曲線可知，軌道系統的實體化對路基動應力的影響體現在幅值上，實體化后動應力幅值減小，但是波形變化不明顯， 循環應力的下限值也基本保持不變.

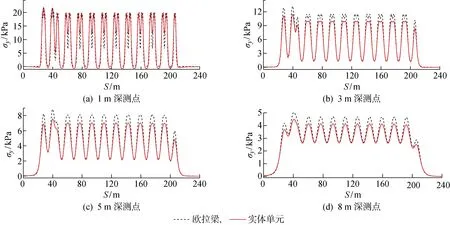
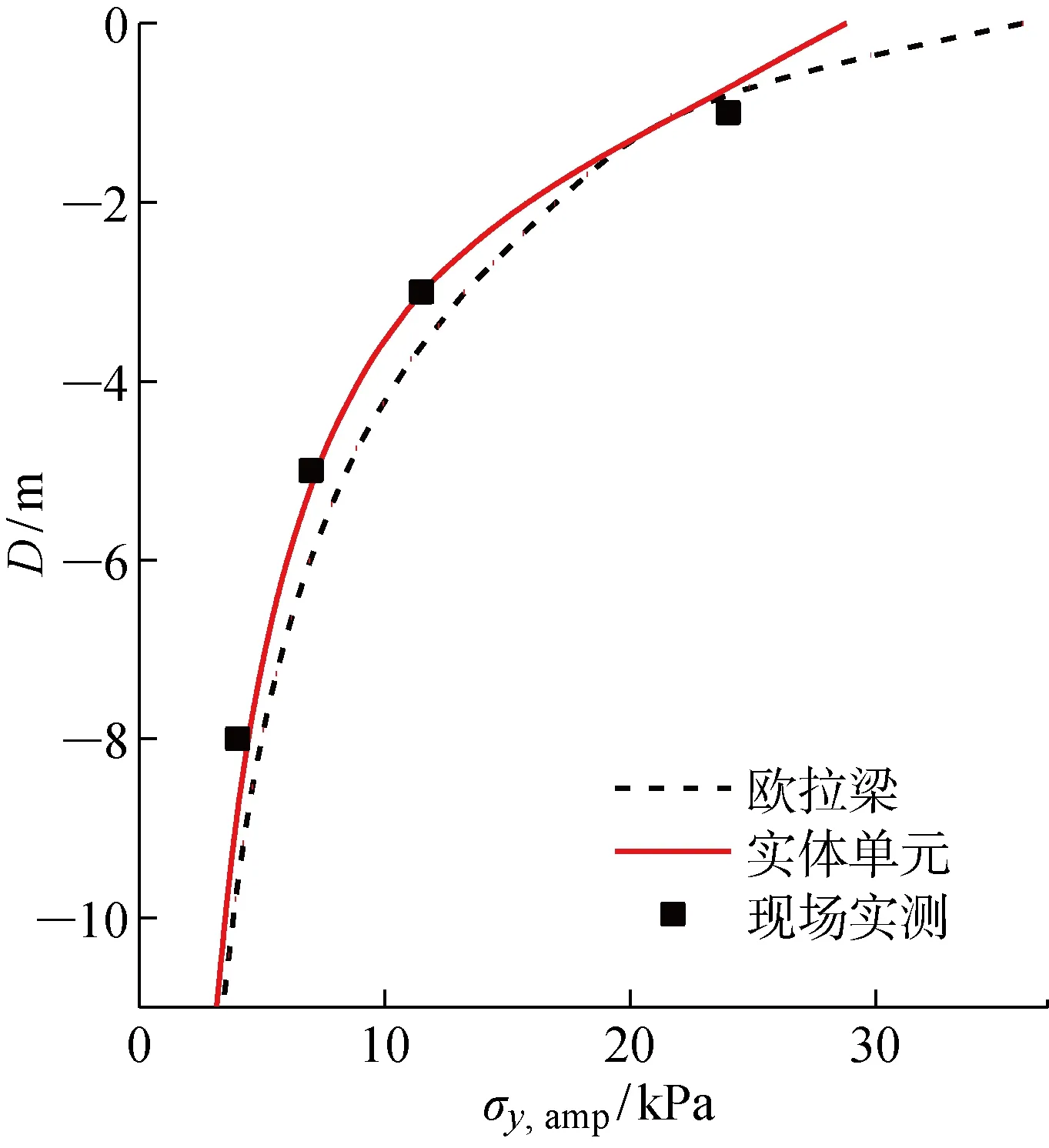
由圖8可知，由于考慮了枕木的橫向剛度，軌道系統實體化后淺層動應力幅值橫向分布呈馬鞍形，更符合路基動應力分布情況.采用歐拉梁模擬軌道系統時基床表層頂面動應力均勻分布且幅值及范圍均偏大.由此導致動應力向下傳遞時影響范圍和幅值偏大.可見在考慮了真實的荷載傳遞路徑之后，道砟-枕木-緊固件的實體化建模使得路基內部動應力分布更為合理.軌道系統的過度抽象會導致路基內部動應力幅值和影響范圍偏大.

“多謝神甫，當時收留我們。不然我們這樣的女人，現在不知道給禍害成什么樣了。”法比這時湊過來，不眨眼地看著玉墨。玉墨又說：“我們活著，反正就是給人禍害，也禍害別人。”她俏皮地飛了兩個神甫一眼。

對比圖9所示路堤中心線處動應力衰減規律可以看出，軌道系統實體化建模后路基內部動應力幅值與現場實測數據更加吻合.另外，本文實體化建模后單元數僅增加44個(共計 1 672 個)，可不考慮其對計算效率的影響.

2.5 土體動力蠕變能耗對路基動力響應的影響

參照已有文獻，將軌道等效為歐拉梁，單根軌道抗彎剛度=6.4 MN·m，單位長度質量=60 kg/m.緊固件單元只考慮其豎向等效模量，其他方向的模量和單元質量設為一極小值.等效模量計算式為

動應力在路基中迅速衰減，因此對不同深度的土層采用差異化的附加阻尼比系數，為了充分體現動力蠕變的影響，設置基床表層、基床底層和路堤本體的附加系數分別為1.0、0.5及0.2.提取附加阻尼前后路堤內部動應力衰減規律如圖11所示.

內筒采用管鞋超前設計。管鞋超前就意味著內筒最前端管鞋具有“吃入”地層的能力，否則將會影響整體鉆進取心效率。因此，將以往取心鉆具中的卡簧座進行優化設計，使其既能放置巖心卡取工具又能高效“吃入”地層。

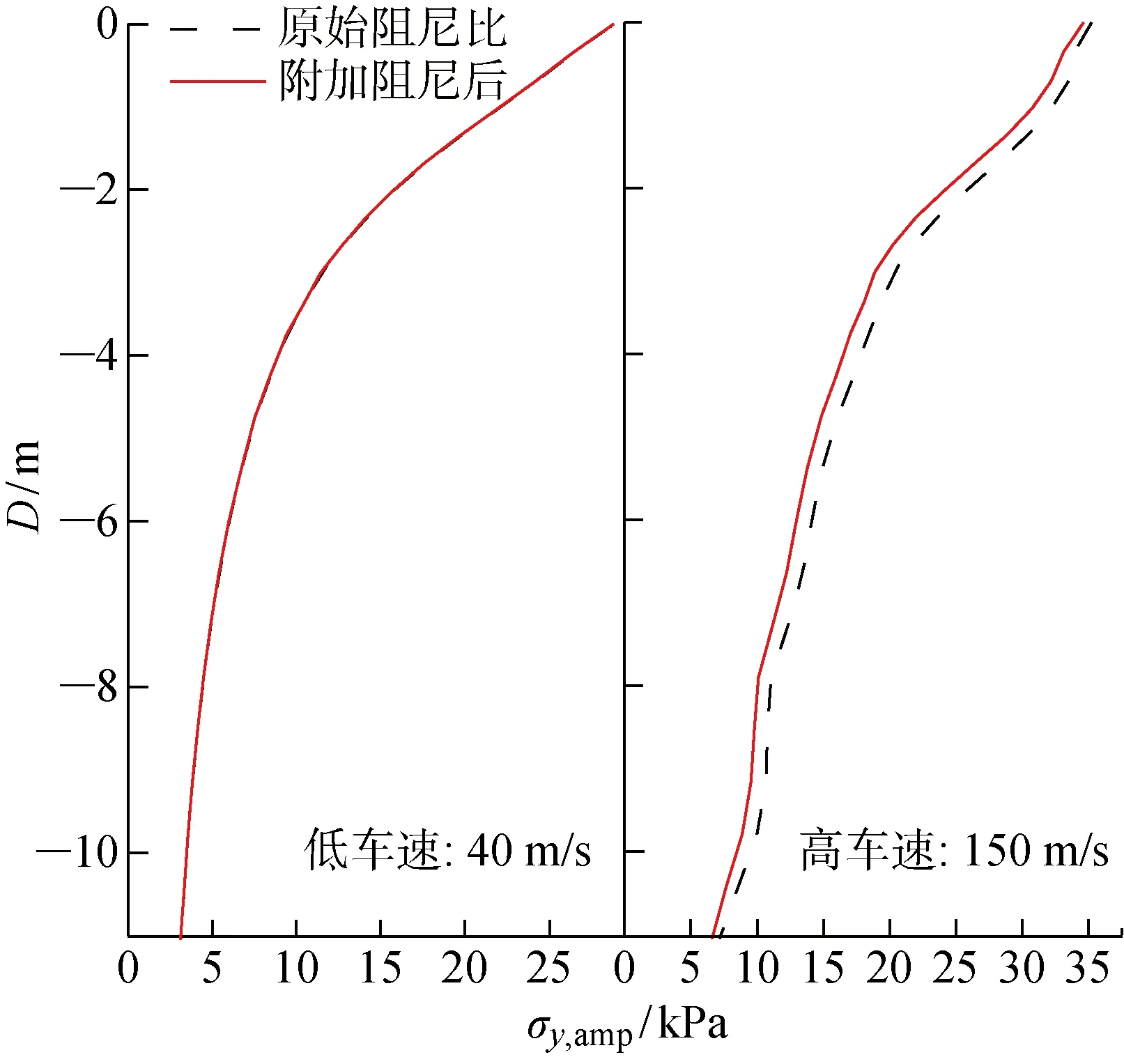
低車速情況下附加阻尼對路基內部動力衰減無影響；高車速時阻尼比增加會輕微減小路基內部動應力幅值.已知40 m/s的車速遠小于基床土體瑞雷波速(約130 m/s)，此時路基屬于擬靜力響應范疇，土體中并無波動傳播，可能導致阻尼比對系統響應影響微弱.

當荷載移動速度大于地表瑞雷波速時會產生波動傳播現象，路基由擬靜力狀態轉換為動力響應狀態.阻尼比的增大會強化路基材料對波動能量的吸收效果，從而減小動應力幅值.本文所涉工程背景不存在高速運行工況，因此在后續分析中不考慮附加阻尼的影響.

(1)通過分析關鍵詞節點大小，可知在整個社會網絡圖譜中，創客教育處于中心位置，對整個網絡圖譜的作用最強。其次是創客、創客運動、創客空間等關鍵詞，反映了當前研究熱點。通過查詢文獻發現，研究主要集中在創客教育與創客、創客運動和創客空間之間的關系等方面。

河南自貿區于2017年正式掛牌成立，由于成立時間尚短，相對于其他發展成熟自貿區來說有關稅收優惠政策相對不夠成熟，但是由于我國自貿區已發展了一段時間，經驗相對豐富，各種稅收政策基本符合國際自貿區的相關稅收慣例，發展相對完善，因此河南自貿區的進出口稅收政策可以參照我國其他發展相對成熟自貿區的進出口稅收政策。除了效仿其他自貿區相關進出口稅收政策之外，河南省自貿區的稅收優惠制度也可隨著我國宏觀政策的變化發生調整，以此來制定出更加適合河南省自貿區小微企業發展的稅收優惠政策。

3 填方路基動力響應規律

基于上述分析，本文采用各向異性實體單元模擬軌道系統，在不考慮動力蠕變能耗的情況下討論新建鐵路和既有線列車運行時圖4中的路基動力響應規律.左側填方場地布置有設備間及辦公、休息區域，因此重點關注新建線路路堤內部動應力分布及填方場地地表環境振動規律.

醫藥B2C平臺顧客忠誠度模型，包括顧客、商品、平臺網站三個方面的因素會對醫藥B2C平臺顧客忠誠度產生正向的影響。如圖1所示。

新建線路為貨運線路，列車運行速度偏低，因此采用圖2所示車輛模型，討論車速較低情況下(10～40 m/s)，路基內部動應力分布及地表環境振動規律.由于缺乏車體動力學參數，暫不考慮軌道不平順影響.既有線為客貨共線鐵路，采用常見的CRH3型車體參數，討論列車在較高速度運行情況下引發的地表環境振動規律，同時評估軌道不平順的影響.

3.1 新建線路列車運行情況下路基響應規律

提取不同車速下路基內部動應力分布規律，如圖12所示.

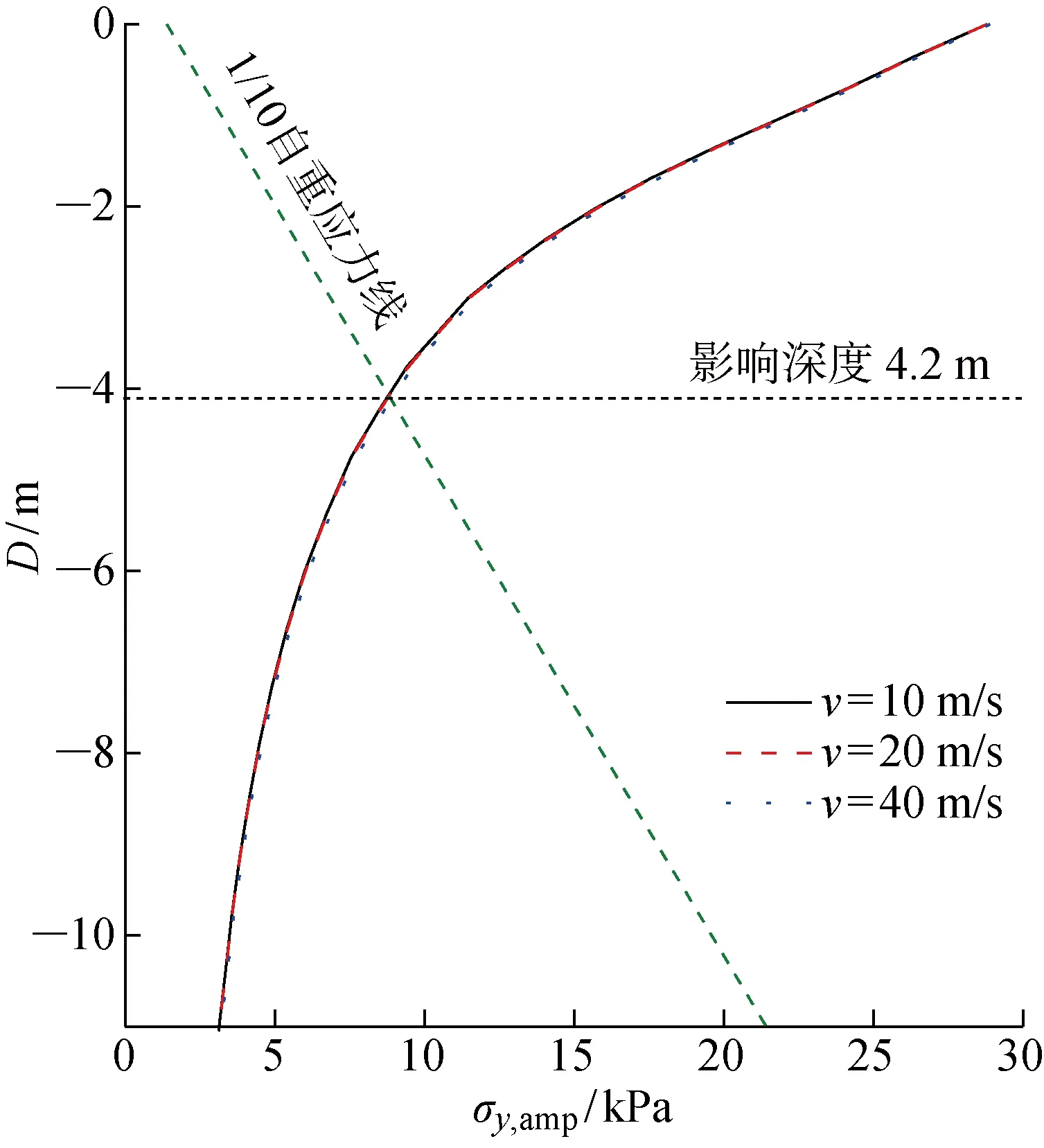
可以看出，貨運列車低速運行情況下，車速對路堤內部動應力分布的影響十分微弱.定義1/10自重應力線與動應力幅值分布曲線的交點所在深度為列車荷載的影響深度.參照《鐵路路基設計規范》TB 10001—2016將道床等上部結構等效為14 kPa的均勻荷載，路基土重度統一取18.5 kN/m.本文工程背景下23 t軸重貨運列車荷載對路基的影響深度約為4.2 m.

采用1/3倍頻程中心頻率的分頻z振級表征列車荷載引發的環境振動，其表達式如下：

=20lg()+

(7)

式中：為該1/3倍頻帶振動加速度有效值；為加速度參考值(取10m/s)；為該1/3倍頻帶中心頻率處的Z計權因子.

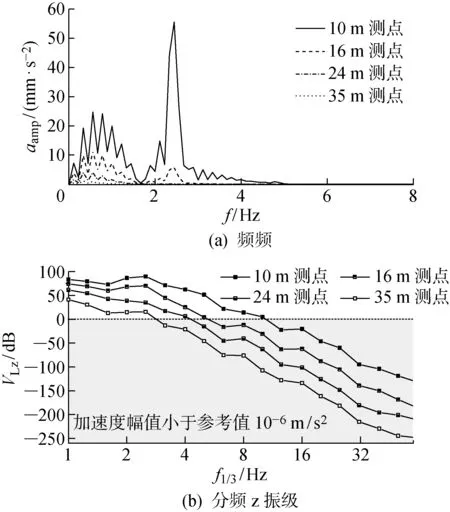
選取左側地表與新建路堤中線水平距離約10、16、24及35 m的4個測點，獲得40 m/s運行速度情況下各測點加速度頻譜及分頻z振級隨1/3倍頻中心頻率變化，如圖13所示.圖中：為加速度幅值；為頻率.可以看出，測點加速度響應集中在 0～4 Hz低頻范圍內.各測點分頻z振級隨中心頻率變化規律類似.

為了分析列車運行情況下場地環境振動沿地表橫向衰減規律，進一步提取地表節點最大分頻z振級分布規律，如圖14所示，圖中為與線路垂直的水平橫向地表位置.隨著列車運行速度的提高，地表環境振動強度逐漸增大但衰減規律類似.行業標準《城市軌道交通引起建筑物振動與二次輻射噪聲限值及其測量方法標準》JGJ/T 170—2009規定4類區域(交通干線兩側區域)建筑物室內振動限值為晝間75 dB、夜間72 dB.當前工況下距離路基中心線15 m以外設備間及辦公區域的最大分頻振級基本不超過72 dB.貨運線路車速一般較低，以往研究重點關注軸重對路基響應的影響，以至于本文所涉貨運內燃機車及棚車車體動力學參數十分鮮見，因此本文暫不考慮新建線路軌道不平順對環境振動的影響.

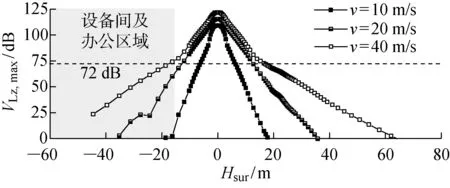
3.2 既有線列車運行引發的地表環境振動規律

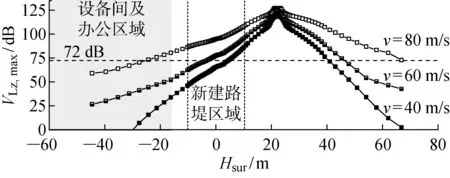
本文僅考慮客運列車以較高車速(40～80 m/s)運行時引發的環境振動規律，車型采用常見的CRH3型客運列車，其軸重及輪對相對位置詳見文獻[20].不同車速情況下路基表面最大分頻z振級分布如圖15所示.可以看出，當列車以80 m/s的速度運行時激發的辦公區域地表環境振動基本滿足要求.環境振動隨測點與加載位置距離的增大近似呈線性衰減的趨勢.另外，最大分頻z振級曲線在新建路堤區域有輕微“上揚”.對比圖14也可以看出，環境振動曲線在經過既有線時有類似“上揚”趨勢.上述現象表明模量較大的地表凸起可能會減緩豎向環境振動的衰減.

其四,藥品劑量會導致處方治療效果具有嚴重變化,很多中藥調配工作人員經常會犯一些常規性的錯誤,就是根據自身感覺調配藥物,沒有經過嚴格的標準進行,導致配制的藥品劑量無法精準,從而影響臨床治療效果,比如紅花藥材,小劑量的紅花具有顯著的養血作用,大劑量則會導致患者發生破血情況發生,還有肉桂,小劑量能夠有效的引火歸原,而大量的肉桂則具有祛寒止痛的功效[5]。另外在實際配置過程當中,需要嚴格注意藥物劑量以及藥物的毒性含量,避免劑量過多導致患者發生中毒情況,在本次研究當中藥品劑量問題占總比的30%。

列車在豎向不平順的軌道上運行時，車體會發生振動從而導致輪軌接觸力的改變.一般車速越高不平順對輪軌力的影響越大.在研究客運列車高速運行誘發的鐵路路基動力響應規律時不宜忽略軌道不平順的影響.本文參考德國高速鐵路高低不平順譜，根據其界定的波長-波高對應關系設定3種不平順參數(參數I～III 的波長分別為2、10、50 m，波高分別為0.15、0.6、2.4 mm)初步評估軌道不平順對環境振動的影響.10自由度車體參數及軌道不平順在2.5D有限元中的實現詳見文獻[28].

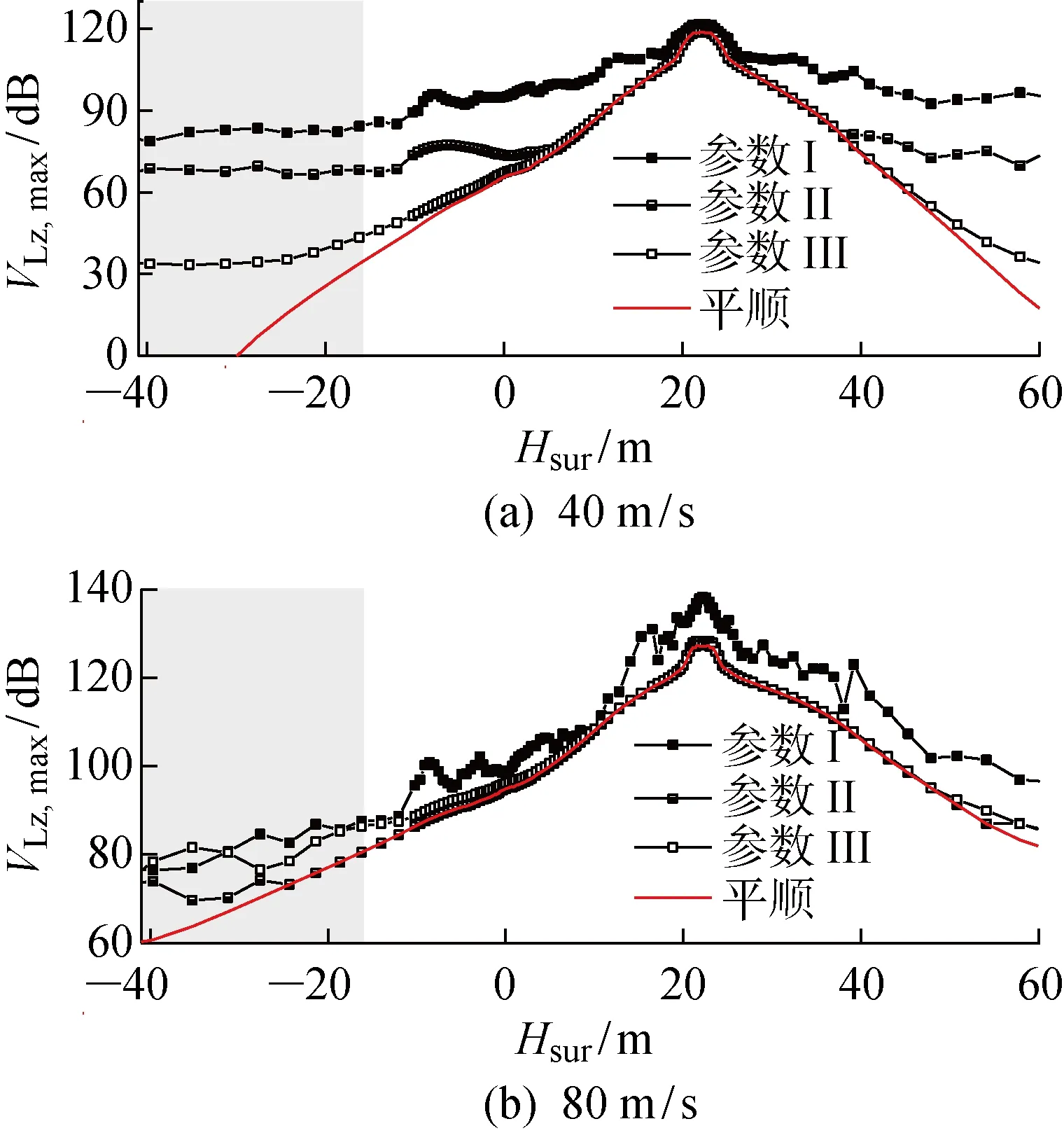
考慮軌道不平順時，既有線列車運行情況下路基環境振動規律如圖16所示.對比平順情況下的響應可以看出，當客運列車以常規車速(40 m/s)行駛時，不平順波長越大，軌道不平順對環境振動的影響越小.在空間上，隨著與加載點距離的增大，不平順對環境振動的影響逐漸顯現，并且存在分叉現象.波長越大，最大分頻z振級曲線的分叉點距離加載點越遠.其原因可能是不平順荷載會激發地基內部波動傳播，使得不平順荷載產生的附加響應在路基內的衰減規律與平順荷載產生的響應衰減規律產生差異，加之式(3)對數取值會放大遠場微小的響應差異，由此產生了明顯的分叉現象.上述現象表明改善軌道短波不平順可以有效控制列車運行誘發的環境振動.

觀察車速較高時(80 m/s)的環境振動規律可以看出，軌道不平順對環境振動的影響減弱.由于本文既有線為非高速鐵路線路，所以對此工況不做過多討論.

4 結論

本文以黃土地區某鐵路專用線工程為背景，通過現場測試得到了填方路堤內部的動應力響應規律，據此驗證了2.5D有限元數值模擬精度并探討了軌道系統各向異性實體化建模及土體動力蠕變對模型動力響應的影響.在此基礎上，分別討論了新建線路運行貨運列車及既有線運行客運列車情況下路基動力響應規律，得出以下幾點結論.

(1) 軌道系統的過度抽象會導致路基內部動應力幅值和影響范圍偏大.由于考慮了真實的荷載傳遞路徑，道砟-枕木-緊固件系統的各向異性實體化建模使得路基內部動應力分布更為合理.

(2) 路基處于擬靜力響應狀態時動力蠕變引發的能量消耗對路基動應力衰減規律的影響可以忽略，路基處于動力響應狀態時動力蠕變引發的能量消耗會減緩路基內部動應力的衰減.

(3) 23 t軸重貨運列車低速運行時，車速對黃土填方路堤內部動應力分布影響微弱，動應力影響深度約為4.2 m.

(4) 隨著地表測點與加載位置間距的增大，軌道不平順對場地環境振動的影響逐漸顯現.車速越低軌道不平順對場地環境振動的影響越明顯.改善軌道短波不平順是控制環境振動的有效措施.