基于合作協議的集裝箱班輪運輸船期設計和加油策略聯合優化

集裝箱班輪運輸是國際工業品和一般消費品海運貿易的主體，承運的貨物具有價值高、種類繁多、交易頻繁、時間性強等特點.為此，船公司需要為客戶提供周而復始的“定線、定船、定期和定港”班輪運輸服務.為了有效地應對集裝箱海運市場需求、燃油價格等因素的變化，通常每隔一段時間(3～6個月)，船公司便需要根據船舶到離掛靠港口時間窗約束進行集裝箱班輪運輸船期設計，以便在滿足客戶集裝箱貨物運輸需求的前提下，實現班輪運輸成本最小化目標.隨著近年來海運供應鏈協同的不斷深化，船公司與碼頭運營商間紛紛簽署船舶到港多時間窗等合作協議，這不僅放松了船舶到港時間窗約束，也為船公司船舶航速調整和加油策略提供了更多的優化空間.尤其是在當前船用燃油價格劇烈波動的新形勢下，研究基于港航合作協議的集裝箱班輪船期設計和加油策略聯合優化問題具有重要的現實意義.

集裝箱班輪運輸船期設計問題最早由文獻[4]提出，在假定航線貨運需求量確定的條件下，其建立了整數線性規劃模型，制定出了船舶到/離港口的船期.文獻[5]進一步探討了在需求隨機波動，但需求均值和方差已知情況下的船期設計問題，構建了非線性混合整數規劃模型.燃油成本在集裝箱班輪運輸成本中占有很大的比例，有文獻研究表明船舶燃油消耗量與速度的立方成正比，故船舶燃油消耗費用與航速成非線性關系，航速優化問題對船公司具有重要的現實意義.據此，文獻[9]建立了以航速為變量的船期問題非線性規劃模型，并設計了線性逼近算法求解.文獻[10]進一步研究了港口具有到達時間限制的航速優化和船期設計問題，建立了非線性規劃模型.考慮燃油價格的波動因素及班輪航線上各加油港燃油價格的差異和折扣情況，文獻[11]以船公司班輪運輸服務總成本最小化為目標函數，建立了船期設計和加油策略的混合整數非線性規劃模型，并選用一條亞歐班輪航線進行了實例研究.上述已有研究，從運輸需求確定到隨機、從船舶航速固定到調整優化、從航線加油港和加油量給定到加油策略選擇等因素方面不斷深化，為班輪運輸經營提供了重要的理論和實踐指導，但研究都是假定船舶到達掛靠港口僅限于某一特定的時間窗內，忽視了船公司與港口碼頭運營商簽署合作協議下的船舶到達港口時間優選問題.

隨著近年來船公司與港口間航運供應鏈融合程度的不斷加深，許多港口碼頭運營商和船公司間簽署了船舶到港多時間窗的合作協議.文獻[13]評估了多時間窗策略，結果發現多時間窗策略不僅能夠影響船舶航速和船期，也能影響班輪運輸服務的總成本.有鑒于此，本文通過引入船公司與碼頭運營商間簽署的船舶到港多時間窗、多起訖時刻和多裝卸速率合作協議，對班輪運輸船期設計和加油策略聯合優化問題開展深入的研究，本文的主要貢獻包括：

(1) 通過分析多時間窗和多裝卸速率下船舶航速與船期設計、加油策略的聯動關系機理，構建基于合作協議的船期設計和加油策略非線性混合整數模型，以實現班輪運輸船期設計和船舶加油的聯合優化.

(2) 引入船舶遲到港口懲罰成本和集裝箱貨物庫存成本，設立包括船舶運營成本、燃油成本、港口裝卸成本、遲到港口懲罰成本和集裝箱貨物庫存成本的班輪運輸服務總成本最小化目標，以實現船公司、港口碼頭運營商和客戶三方共贏.

(1) 班輪航線配置的集裝箱船舶類型相同.

(3) 結合船舶駕駛操縱實際，設計先對船舶航速變量加以離散化、再對模型進行線性化的求解算法.在航運實際背景下進行大規模算例模擬驗證分析，以便為航運供應鏈深度融合新形勢下的集裝箱班輪運輸實踐應用提供決策參考.

1 問題描述及基本假設

1.1 問題描述

在航運供應鏈協同的背景下，為了提高港口碼頭作業和船公司班輪運輸組織的效率和效益，船公司紛紛與各船舶掛靠港口碼頭運營商簽署船舶到港多時間窗、多起訖時刻和多裝卸速率合作協議.某船舶到港時間窗有3個開始時刻和3個結束時刻，如圖1所示.

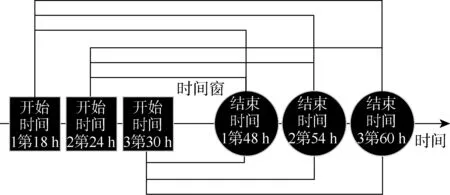
由圖1可知，船舶到港時間窗的3個可選開始時刻分別為第18 h，第24 h和第30 h，3個可選的結束時刻分別為第48 h，第54 h和第60 h.假設第 0 h 為星期一凌晨0點，則到港時間窗的3個開始時刻分別為星期一下午6點、星期二凌晨0點和早上6點；3個結束時刻分別為星期三凌晨0點、早上6點和中午12點，由此可組合出9個不同時段或長度的時間窗.考慮到集裝箱碼頭泊位可用時間資源的稀缺性，這里將船舶到港時間定義為船舶靠泊碼頭的時間.此外，結合碼頭岸橋等裝卸設備的使用情況，港口碼頭運營商還可提供多種不同費率下的集裝箱裝卸速率供船公司選擇.

為了滿足托運人在航線各港口每周的集裝箱運輸需求，船公司在保證發船頻率為周班的條件下，船舶一個往返航次時間(從某一始發港出發，順序途徑各掛靠港裝卸貨物，最終返回始發港所花費的時間)應為周的整數倍，該整數亦應為航線配置的船舶數量.于是，船公司的船期設計和加油策略問題將包含以下決策內容：① 確定航線船舶配置數量和各航段上船舶的航行速度；② 選定船舶到達和離開港口的時間；③ 選定各掛靠港口的集裝箱裝卸速率；④ 選擇加油港口并確定加油量.決策目標是使船公司的班輪運輸服務總成本(包括航線上所有配置船舶的周運營成本、周燃油成本、周港口裝卸成本、周集裝箱貨物庫存成本和周遲到港口懲罰成本)最小化.其中，遲到港口懲罰成本是指船舶未能在港口提供的時間窗內按時到達停靠的泊位，發生時間延遲需要承擔的懲罰成本.

1.2 基本假設

為了便于建模，本文結合實際作出以下基本假設：

作為新型的銀行業金融機構，村鎮銀行具有無歷史包袱、決策鏈條短、貼近市場一線、機制體制靈活等優勢。但由于受到面向的“三農”、產業的弱質性、面對客戶群體的復雜性、所處社會信用環境的脆弱性等因素制約，村鎮銀行強化內部審計策略開展內部審計顯得非常必要。

(2) 班輪航線船舶掛靠港口及順序確定.

(3) 班輪航線發船頻率為周班.

2 優化模型構建

2.1 燃油成本函數

船舶每天燃油消耗量通常與航速的立方成正比，但考慮到其還與動力裝置、自然條件等多種因素密切相關，故可建立船舶在航段燃油消耗量函數為

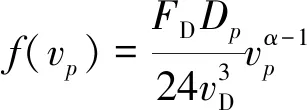
(1)

?∈

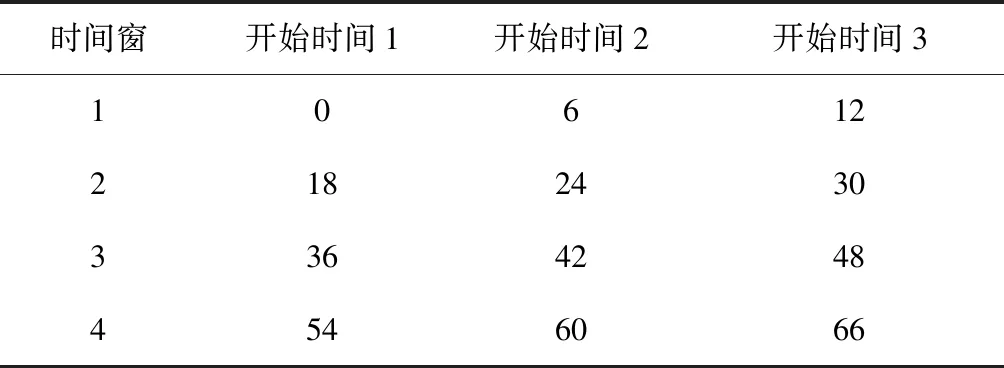
式中：(≈3)為船舶燃油消耗速度函數系數，其與船型及航段航行條件等因素相關，可由船舶實際航行統計數據加以校準確定；為船舶在設計航速下每天的燃油消耗量；為航段(即港口至港口+1)距離；={1, 2, …,}為班輪航線上港口的集合，為港口總數，為港口至港口1的距離；為船舶的設計航速；為船舶在航段(即港口至港口+1)上的航速.

于是，船舶一個往返航次的燃油消耗量應等于加油量，即：

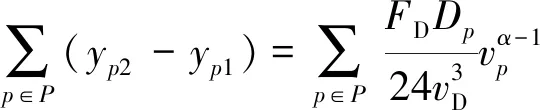
(2)

?∈

式中：1為船舶到達港口時的燃油庫存水平；2為船舶離開港口時的燃油庫存水平.

由于班輪航線上船舶掛靠的加油港口相距較遠，燃油價格差異較大，加之可能存在價格折扣因素，所以，船舶的加油費用與加油港選擇和加油量的確定密切相關.若船舶在港口加油有兩次折扣，則船舶在港口的加油費用函數可以表示為

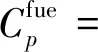
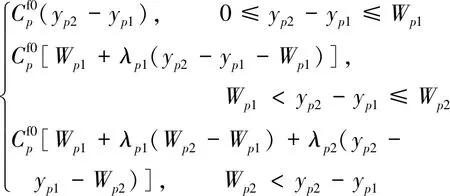
(3)

?∈

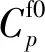
因此，船舶一個往返航次的燃油成本為

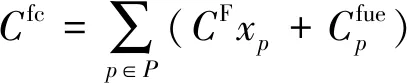
(4)

?∈

式中：為0-1變量，即若船舶在港口加油，則等于1，否則等于0；為船舶加油固定費用.

2.2 目標函數

由式(2)和(4)可建立一個船舶往返航次燃油消耗費用與航速間的聯系，據此便可建立船期設計和加油策略聯合優化模型[M1].

..時間窗長度變化的影響 船舶到港時間窗長度是船公司與各港口碼頭運營商簽署合作協議中的一項重要條款，是船期設計和加油策略問題需要考慮的一項重要因素.本文將時間窗長度由均勻分布[24, 29] h隨機生成，逐漸遞增至由均勻分布[69, 74] h隨機生成，構造11組時間窗長度由小到大的算例，每組算例由 1 000 個按上述規則隨機生成的模擬場景組成，求解得到不同時間窗長度下各模擬場景班輪運輸一個往返航次總時間最優值均為 1 176 h(7周)，最優配船數均為7艘，船舶加油量各模擬場景的平均值如表6所示.

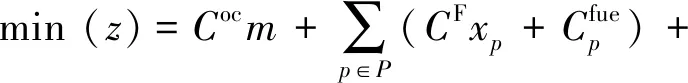
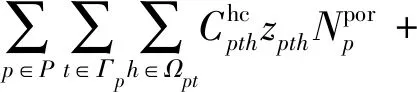
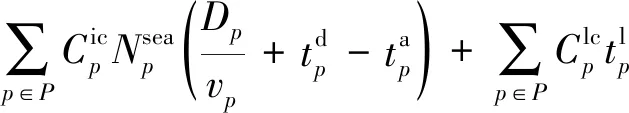
(5)

?∈，?∈，?∈

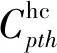
2.3 約束條件

船舶在港口的加油量約束可表示為

01≤2-1≤，?∈

(6)

式中：為船舶油艙的最大容量.

船舶航次的初始燃油量可表示為

=

(7)

式中：為船舶初始燃油量.

船舶在進出港口時的油量約束可分別表示為

中國的磷肥工業“大器晚成”，從過：磷酸鈣、鈣鎂磷肥、硝酸磷肥、磷酸銨到現在的磷復肥，整整摸索了半個世紀之久。在1953年開始的第一個國民經濟“五年計劃”中，國家確定了磷肥工業實行酸法、熱法并舉的方針，重點安排在南京和太原分別建設兩個年產40萬噸和20萬噸的普鈣廠。1958年，南京磷肥廠率先建成投產，宣告了我國磷肥工業的誕生。5年后，利用大煉鋼鐵時代留下的高爐，我國科學家在江西撫州市東鄉磷肥廠成功研制出可以直接使用16%P2O5低品位磷礦作原料的鈣鎂磷肥。

1≥01

(8)

2≤

(9)

?∈

各航段上船舶航行的燃油消耗量可分別表示為

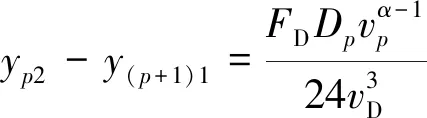
(10)

?∈,<

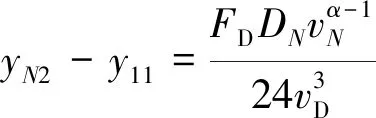
(11)

船舶只選擇一個時間窗到達港口可表示為

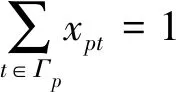
(12)

?∈，?∈

式中：為0-1變量，即若船舶在港口選擇時間窗內到達，則等于1，否則等于0.

由于模型[M1]為一個非線性混合整數模型，目標函數式(5)中既含有航速變量的倒數項，約束條件式(10)和(11)中又含有變量的冪次方項；式(22)～(26)中均含有變量的倒數項，所以難以直接求解為此，本文將模型中的變量替換為其倒數=1，則式(22)～(26)均可變為線性約束，但是式(10)和(11)仍為非線性約束接下來，本文采用先對變量取離散值，再對式(10)和(11)中的燃油消耗量函數線性化處理的方法進行模型求解.

船舶只能在選定的時間窗內選擇一個開始時刻進行裝卸作業，可表示為

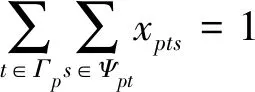
(13)

≤

(14)

?∈, ?∈, ?∈

式中：為0-1變量，即若在港口選擇時間窗的開始時刻，則等于1，否則等于0；={1,2, …,}為港口時間窗開始時刻的集合，為開始時刻總數.

基于圖像技術的破碎卵石指標相關性對比分析…………………………………… 張蘇花，高占須，郭慶林（5-279）

船舶只能在選定的時間窗內選擇一個裝卸作業結束時刻可表示為

根據已有研究，在現澆混凝土中添加HEA-JL型抗裂防水可以保證接觸界面的黏結強度，提高接觸界面的拉拔、劈裂以及抗折強度，減小混凝土的收縮變形，而且可以使局部現澆段有很好的防水能力.選用聚丙烯纖維硅灰水泥漿的界面劑[12]，可以使現澆混凝土與預制混凝土之間緊密結合，二者形成良好的黏結強度，減少混凝土裂縫，將裂縫細化[13].

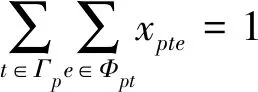
(15)

≤

(16)

?∈, ?∈, ?∈

式中：為0-1變量，即若在港口選擇時間窗的結束時刻，則等于1，否則等于0；={1,2, …,}為港口時間窗結束時刻的集合.

的表情好像在說想想辦法吧。我像美國人似的聳聳肩膀，流露出無可奈何的表情。沉悶而煩躁的氣氛充滿了電梯。好像是壞了。要按緊急鈴嗎？女人焦急地說。那好吧。我點頭說道。女人先是緩慢地，后來幾乎是神經質地去按紅色的“呼叫”按鈕。女人按得手指都紅了，終于放棄了。下面好像沒有人。時間漸漸流走。我和女人用力敲電梯門，想告訴外面的人我們被困在電梯里面了。我們手腳并用，把門敲得咣當咣當。敲著敲著，我說，如果再這樣捶下去，說不定電梯受到沖擊墜落下去。女人滿臉恐懼，停止了敲門。今天早

據此，可對船舶航行燃油消耗量函數()進行離散化，如圖2所示.

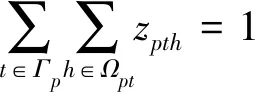
(17)

≤

(18)

?∈, ?∈, ?∈

船舶在港裝卸時間約束可表示為

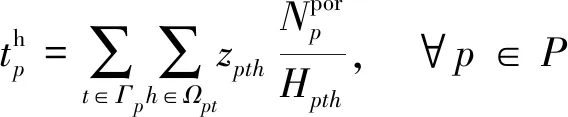
(19)

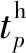
船舶離開港口的時刻約束可表示為

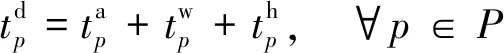
(20)

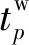
船舶遲到港口的時刻約束可表示為

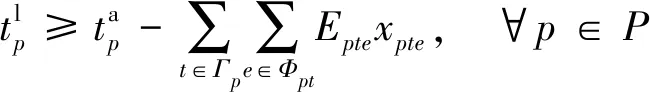
(21)

將本文模型[M2]與文獻[11]的模型[M3](考慮各加油港燃油價格差異和折扣因素，無合作協議)和文獻[15]的模型[M4](不考慮各加油港燃油價格差異和折扣因素，有合作協議)進行算例結果對比分析，以驗證本文模型的有效性和適用性.計算得出3個模型[M2]，[M3]和[M4]在各模擬場景下，船舶一個往返航次總加油量及各項成本的最小值、平均值和最大值優化結果，如表5所示.

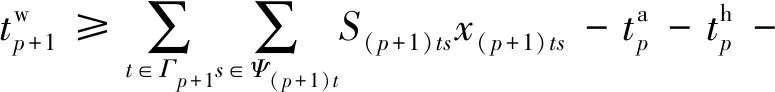
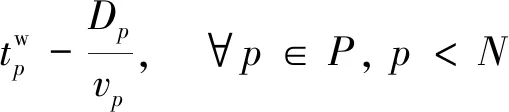
(22)

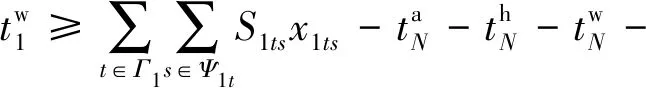
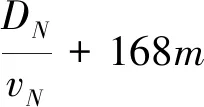
(23)

船舶到達港口的時刻約束可表示為

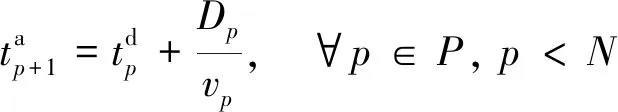
(24)

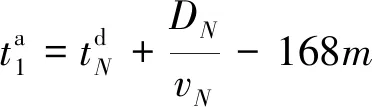
(25)

船舶一個往返航次的時間應為周的整數倍，也等于168 h(1周)乘以航線上配置的船舶數量，則有：

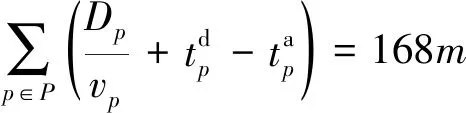
(26)

船舶航速范圍限制可表示為

通過高中數學課程的學習，學生能夠在具體的真實情境中積累經驗，形成抽象思維，把握事情的本質，運用數學抽象的思維方式思考并解決實際問題．在2018年的高考數學命題中，對學生數學抽象核心素養的考查已經落實到具體的題目當中，凸顯高考數學命題鮮明的素養導向和育人導向．

≤≤，?∈

(27)

式中：為船舶最小航行速度；為船舶最大航行速度.

航線上配置的船舶數量約束可表示為

≤

(28)

式中：為航線上允許配置的船舶最大數量.

3 模型求解

3.1 模型分析

本文所開發的電動機適用于上海振華港口機械(股份)有限公司風電齒輪箱試驗臺(ZP11-1627)所用的變頻電動機項目。該項目采用的變頻器為ACS6000，最大輸出電壓為3 100 VAC。用戶對電動機的基本參數要求如下。

3.2 模型轉化

在實際船舶駕駛操縱中，船長設定的航速取值通常到小數點后一位，即到0.1 kn.文獻[15]的研究表明，將航速變量區間[15, 25] kn劃分50等份(即航速間隔長度小于等于0.2 kn)進行離散取值，便可滿足船舶航行燃油消耗量函數離散化的精度要求.因此，本文采用0.1 kn為等間隔長度對變量進行離散取值符合理論和實踐要求，即令

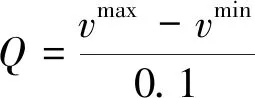
(29)

于是，可將船舶航速等間隔地離散為+1個取值，則有：

=+01,∈{0, 1, …,}

(30)

無人機遙感技術主要由無人機以及無人機遙控器構成，其中主要分為以下三個部分。第一部分是地面系統，包括地面上的無人機遙控器等其他輔助設備。第二部分是任務的載荷系統，其中包括火控系統以及探測目標等有關系統。第三部分是無人機部分，主要指的是無人機主機。無人機一般較為輕盈小巧，結構較為簡單，因此在飛行時極為靈活，操作較傳統的航拍更為簡單，并且可以呈現出更加清晰的畫面以及分辨率更高的反饋圖像[1]。

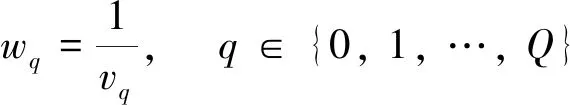
(31)

船舶只能在選定的時間窗內選擇一個集裝箱裝卸費率進行作業，可表示為

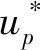
為了便于模型求解，定義0-1變量，則有：

=

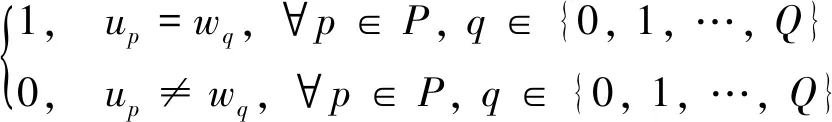
(32)

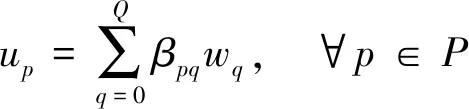
(33)

由此，模型[M1]可以轉化為如下模型[M2].

目標函數：

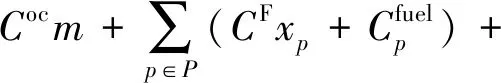
——近日，中共中央辦公廳印發《關于深化中央紀委國家監委派駐機構改革的意見》，對此，中國政法大學副校長馬懷德表示，推進全面從嚴治黨，責任主體在駐在部門黨組（黨委），派駐機構作為紀委監委的重要組成部分，通過實施有效監督，督促駐在部門黨組（黨委）履行應盡之責。（《中國紀檢監察報》11月5日）

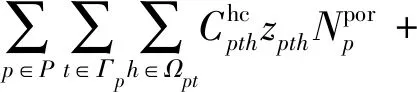
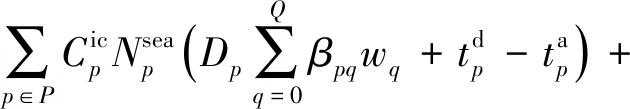
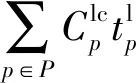
(34)

約束條件：

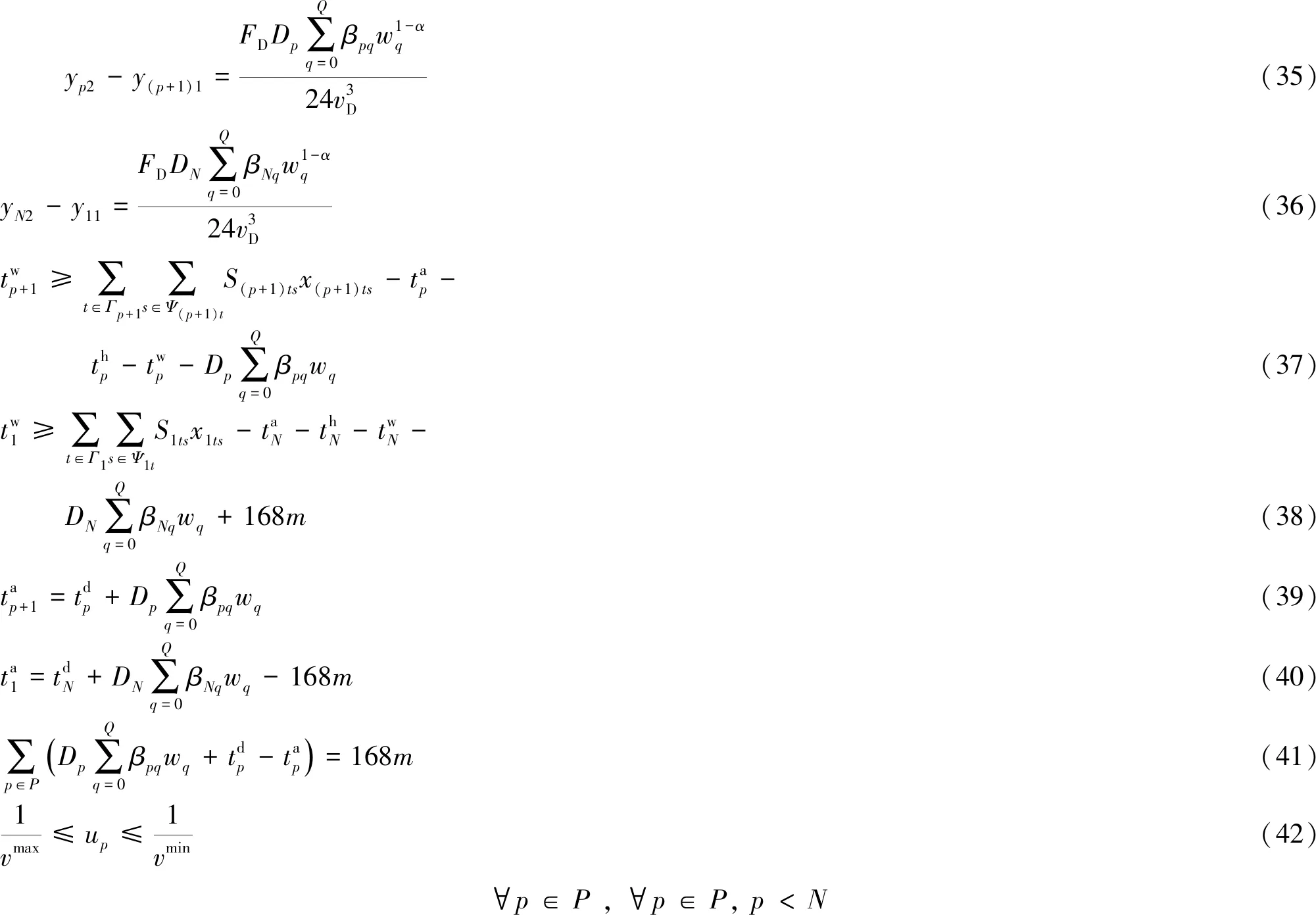
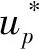
4 實例數值分析

4.1 數據收集與處理

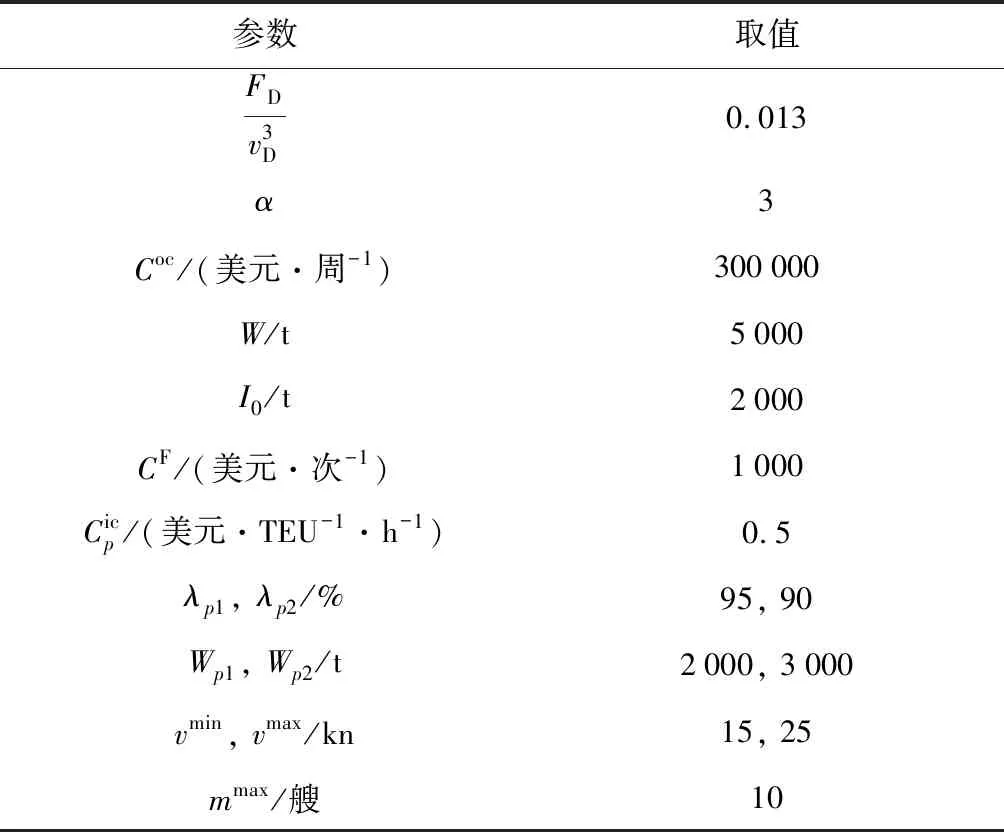
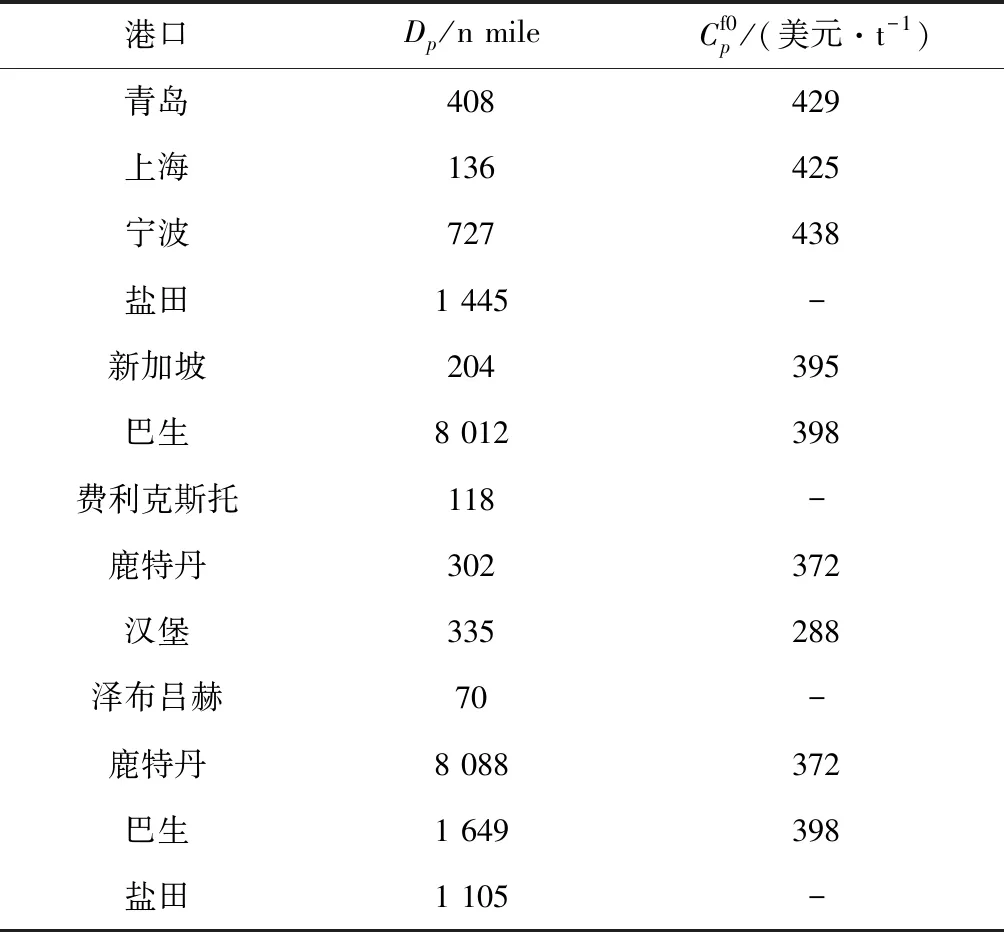
以中國遠洋海運集團有限公司的集裝箱班輪AEX1航線為例，該航線上船舶一個往返航次掛靠港口依次為：青島—上海—寧波—鹽田—新加坡—巴生—費利克斯托—鹿特丹—漢堡—澤布呂赫—鹿特丹—巴生—鹽田—青島，共計掛靠13個港口(船舶掛靠一次計一個港口).參照文獻[11, 16, 19]，本文的相關參數數據設置如表1所示.其中：TEU為以長度為6.096 m的集裝箱為國際計量單位，也稱國際標準箱單位.

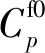
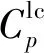
假設各港口向船公司提供4個船舶到港時間窗，每個時間窗分別有3個開始時間和3個結束時間.其中，航線上第1個港口青島港提供的4個船舶到港時間窗，以及每個時間窗的開始時間如表3所示.

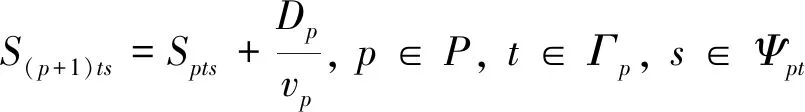
世行：發展中國家近三十年收入階層固化嚴重。5月9日，世界銀行（世行）發布世界各國收入階層流動性報告指出，過去三十年，發展中國家人口從低收入階層向高收入階層流動基本陷于停滯。整體上看，發展中經濟體社會底層人群向上流動性下降，陷于底層人數增加；國別來看，不同發展中國家流動性亦存在巨大差異。

4.2 算例計算

考慮到算例中存在一些隨機產生的數據，故首先按上述規則隨機生成 1 000 個(保證算例數據的充分性)場景，然后在Pentium(R) i5 3.10 GHz 內存為4 GB的電腦上利用ILOG CPLEX 12.6軟件進行算例數值分析，得到在 1 000 個場景中船舶最早、平均和最遲到/離各掛靠港的船期，以及在各加油港最小、平均和最大加油量優化結果，如表4所示.

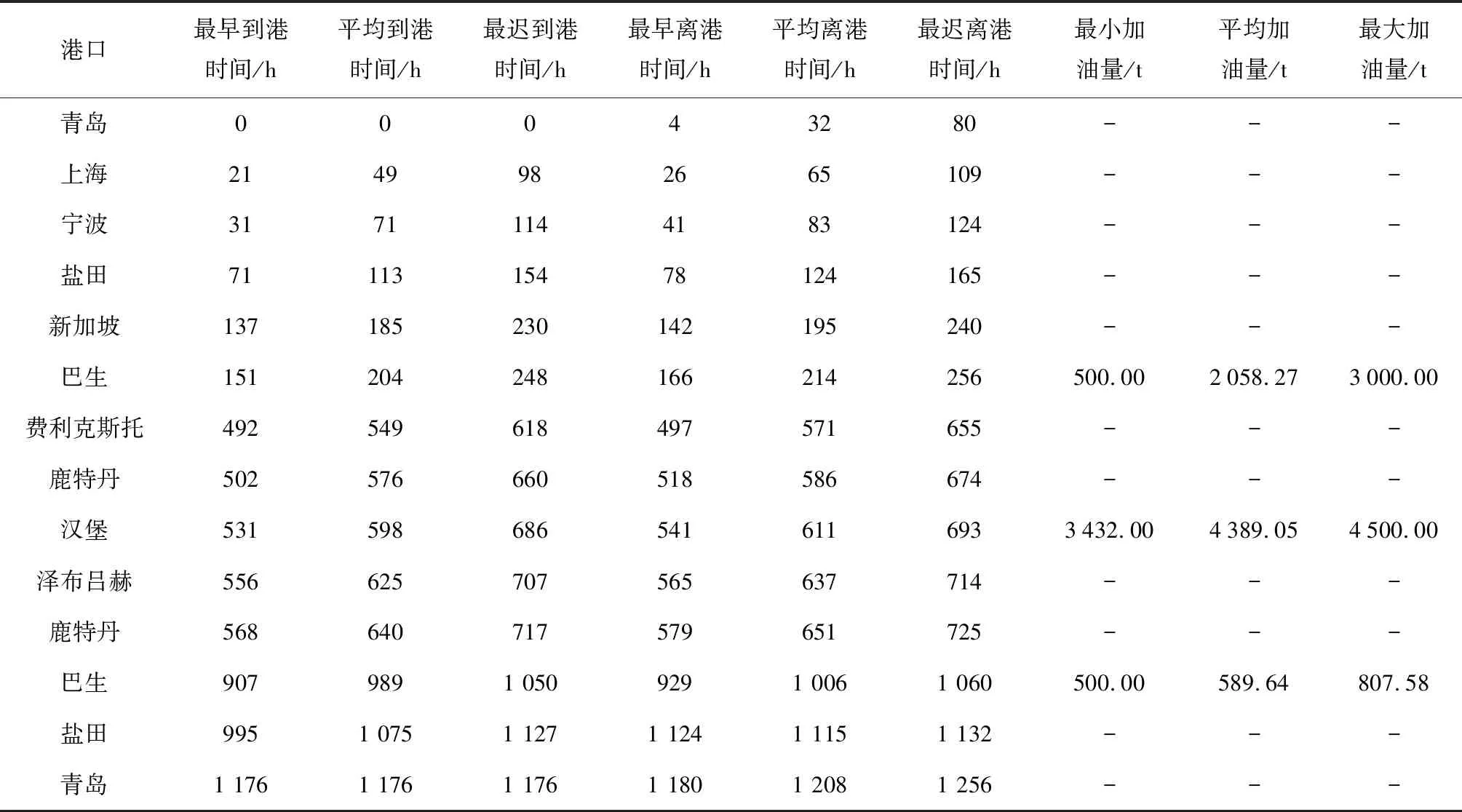
由表4可見，在各個模擬場景下，船舶一個往返航次的總時間均為 1 176 h(7周)，因而該班輪航線的配船數量均應為7艘，且船舶一個往返航次的加油港口也均保持不變，即巴生(去程)、漢堡和巴生(回程).但船舶到/離各港口的最早和最遲時間，以及在各加油港口加油量的最小和最大值均存在較大差異.這表明盡管在上述各個模擬場景下，班輪航線配船數和船舶加油港保持不變，但由于船舶到/離各港口時間及加油量與船舶在各港口裝卸的集裝箱數量、各港口碼頭運營商提供的時間窗和裝卸速率等因素密切相關.因此，在班輪運輸船期設計和船舶加油實際決策中，船公司應通過統計分析船舶在各港口裝卸集裝箱數量真實數據，并與碼頭運營商簽署有效的合作協議，獲取確切的船舶到港多時間窗、多起訖時間和多裝卸速率數據，以確定符合實際的船舶到/離各港口時間及加油量.

近日，2018年聯合國中國美食節暨寧夏賀蘭山東麓葡萄酒走進聯合國活動，在聯合國總部代表餐廳舉辦，來自寧夏21家酒莊的葡萄酒擺上餐桌供各國嘉賓品鑒。賓客們均被寧夏葡萄酒優秀的表現所征服。本次活動聯合國代表餐廳已決定把賀蘭神等20款寧夏葡萄酒作為今后聯合國的采購用酒。

船舶在后一個港口的等待時間約束可表示為

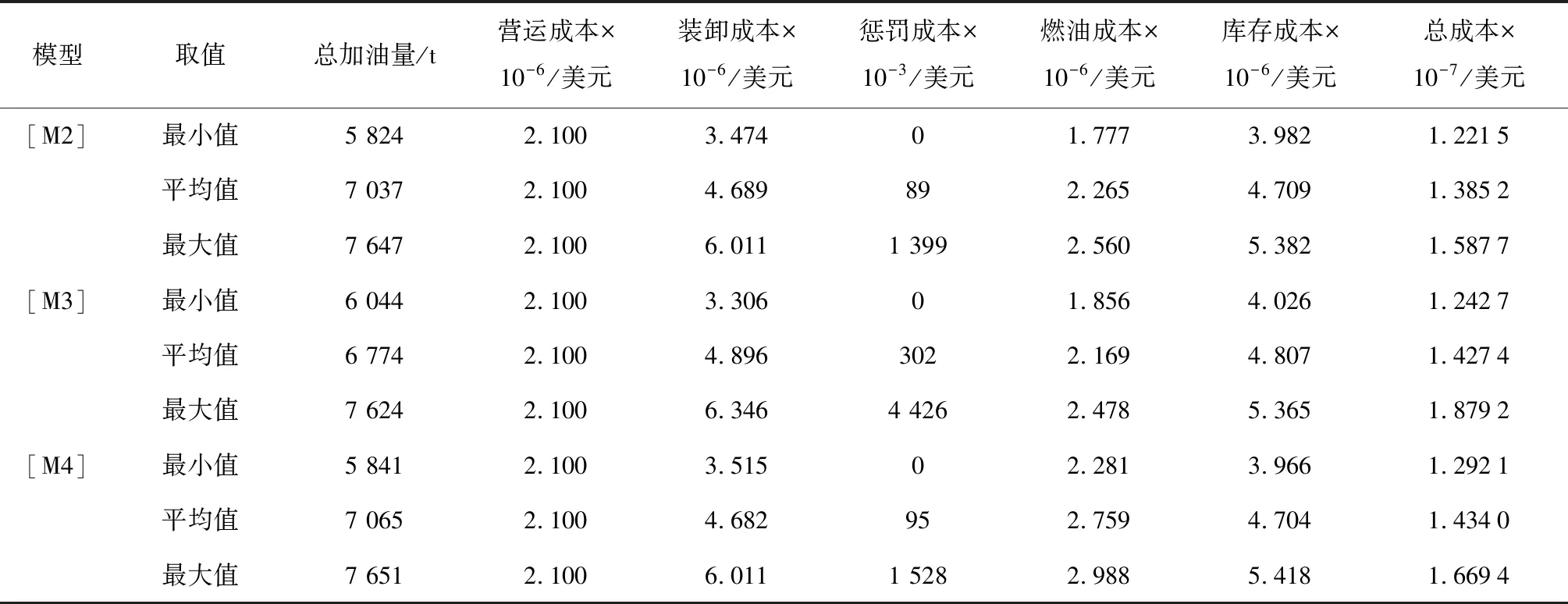
由表5可見，在各模擬場景下各模型得到的船舶營運成本均相同，表明航線配船數量均為7艘.從最小值看，模型[M2]得到的航次總加油量(亦即燃油消耗量)和燃油成本比模型[M3]和模型[M4]的都低；從平均值和最大值來看，模型[M2]得到的航次總加油量(亦即燃油消耗量)和燃油成本比模型[M3]的高，比模型[M4]的低.其他各項結果對比顯示，模型[M2]得到的船舶遲到港口懲罰成本均比[M3]和[M4]的低；模型[M2]得到的裝卸成本、集裝箱貨物庫存成本比模型[M3]的低，比模型[M4]的略高.

此外，模型[M2]得到的所有場景班輪運輸服務總成本最小值、平均值和最大值均最低，從平均值上看，比模型[M3]的節省了3.0%，比模型[M4]的節省了3.4%.究其原因，是由于與模型[M3]相比，模型[M2]考慮了在港口碼頭運營公司與船公司簽署合作協議下，船公司擁有了多時間窗、多起訖時刻和多裝卸速率等多項選擇，這樣船公司便可以通過優化提高船舶航速，雖然使得船舶燃油消耗量和燃油成本有所增加，但卻可以更為靈活地選擇船舶到離港口時刻和裝卸速率，較為明顯地降低了裝卸成本、遲到港口懲罰成本和集裝箱貨物庫存成本，使班輪運輸服務總成本得到顯著降低.與模型[M4]相比，模型[M2]考慮了各港口的燃油價格差異和折扣因素，使得船公司可以選擇在油價較低的加油港加油，且可以選擇多加油以享受油價折扣，使得航次燃油成本得到明顯減少.這樣以來，雖然得到的船舶平均航速、航次裝卸成本、遲到港口懲罰成本和集裝箱貨物庫存成本等結果沒有明顯的差別，但模型[M2]得到的班輪運輸服務總成本明顯降低.由此可見，本文模型比已有文獻研究模型更為有效.

4.3 敏感性分析

值得注意的是，恩替卡韋能更快使ALT復常及HBV‐DNA、HBeAg轉陰，縮短了療程，而阿德福韋酯則需更長的治療時間，所以費用也會隨之增加，而且還可能因用藥時間延長而出現耐藥，耐藥會使HBV變異。前有研究已證明，拉米夫定的耐藥率最高，恩替卡韋最低［11］。照此看來，從長遠考慮，阿德福韋酯的藥物經濟學價值并不一定高，而高效、低耐藥的恩替卡韋可能反而更為經濟，適合長期抗病毒治療。有待進一步研究。

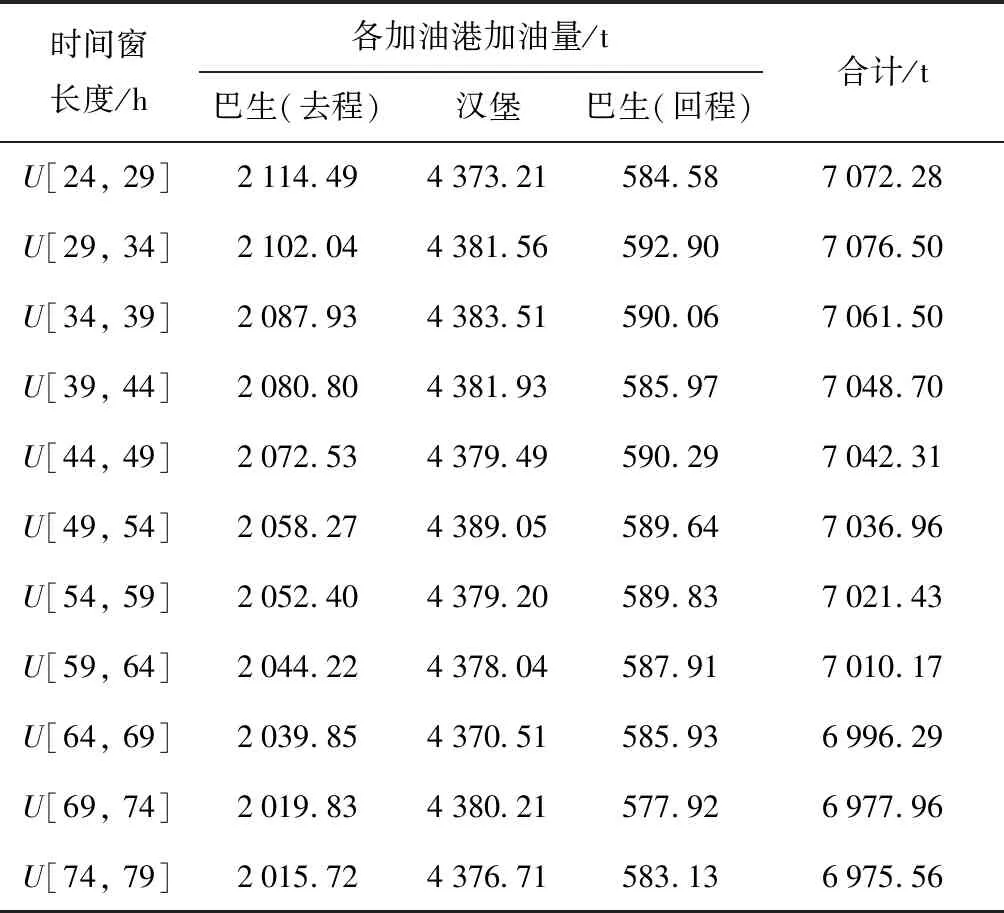
由表6的各模擬場景加油量平均值可以看出，隨著船舶到港時間窗長度的擴大，在巴生(去程)加油量隨著時間窗長度范圍的擴大而不斷減少，其他兩個港口加油量變化不太明顯，船舶一個往返航次的總加油量逐漸減少.究其原因，是因為隨著船舶到港時間窗長度的擴大，船公司可以更加靈活地調慢航速，從而減少燃油消耗量，有助于船舶節能減排.

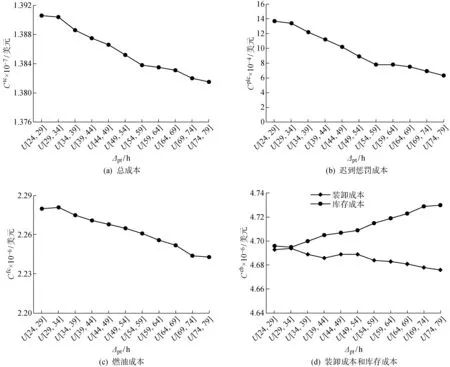
隨著船舶到港時間窗長度的變化，船舶一個往返航次各項成本在各模擬場景下的平均值如圖3所示.其中:為總成本；為遲到懲罰成本；為成本統稱.

農村人口眾多，由此產生的垃圾數量龐大，而且種類繁多，包括生活垃圾、廚余垃圾、生產垃圾等。這些垃圾的成分復雜，有很大一部分很難自然降解，甚至有毒有害，對農村環境有很大影響。

由圖3的各模擬場景平均值可以看出，隨著船舶到港時間窗長度的擴大，船公司班輪運輸服務總成本、船舶一個往返航次遲到港口懲罰成本、燃油成本及裝卸成本都呈降低的趨勢，船舶一個往返航次庫存成本呈升高的趨勢.這是因為，船舶到港時間窗長度越大，船公司便越能靈活地調慢船舶航速，越能減小船舶遲到港口的可能性，并越容易選擇較低的裝卸作業速率裝卸集裝箱貨物，因而越能降低船舶遲到港口懲罰成本、燃油成本和裝卸成本.同時，船舶到港時間窗長度越大，越會容易造成船舶在港裝卸時間的延長，因而越會導致一個往返航次庫存成本的增加.但由于庫存成本所占比例較低，所以隨著船舶到港時間窗長度的擴大，班輪運輸服務總成本仍呈降低的趨勢.

..燃油價格變化的影響 燃油成本是班輪運輸成本的主要構成部分，本文在表2給出的各掛靠港口燃油價格的基礎上，按燃油價格變化率()由 -30%～+60%遞增構造10組算例，每組算例由 1 000 個按上述規則隨機生成的場景組成，求解得到不同燃油價格變化率下班輪運輸一個往返航次總時間最優值均為 1 176 h(7周)，最優配船數均為7艘，船舶加油策略各模擬場景平均優化結果如表7所示.

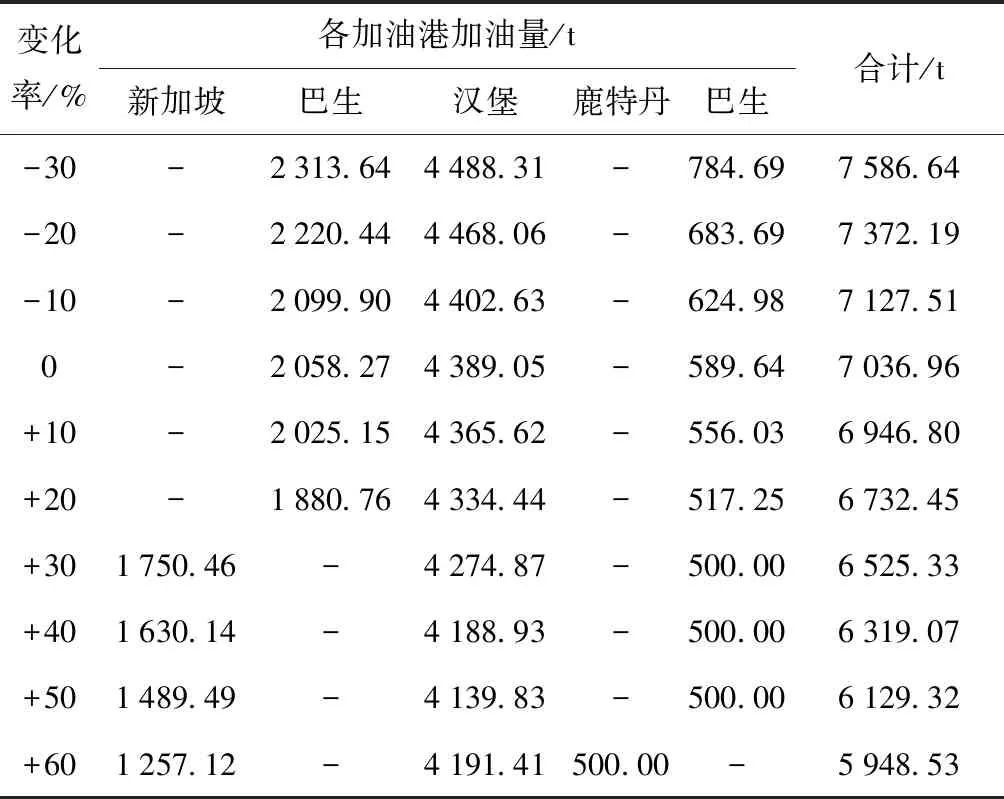
由表7的各模擬場景平均值可以看出，當燃油價格變化率在 -30%～+20%時，隨著燃油價格變化率(亦即燃油價格)的升高，船舶在巴生(去程)、漢堡、巴生(回程)等港口的加油量均呈減少的趨勢；當燃油價格變化率在+30%～+50%時，新加坡取代了巴生(去程)成為新的加油港口，且隨著燃油價格的升高，船舶在新加坡的加油量逐漸減少，在漢堡的加油量有增有減，在巴生(回程)的加油量保持不變；當燃油價格變化率為+60%時，鹿特丹取代了巴生(回程)成為新的加油港口.此外，隨著燃油價格的升高，一個往返航次船舶總加油量呈逐漸減少的趨勢.究其原因，是由于高速航行會造成燃油成本乃至周班輪運輸服務總成本均急劇升高，因此，船公司需要降低船舶航速，從而減少燃油消耗量及一個往返航次船舶的總加油量.

此外，當燃油價格變化率在 -30%～+60%時，隨著燃油價格的升高，計算得出3種模型[M2]，[M3]和[M4]船舶一個往返航次各模擬場景的總成本平均值敏感性分析對比結果如圖4所示.

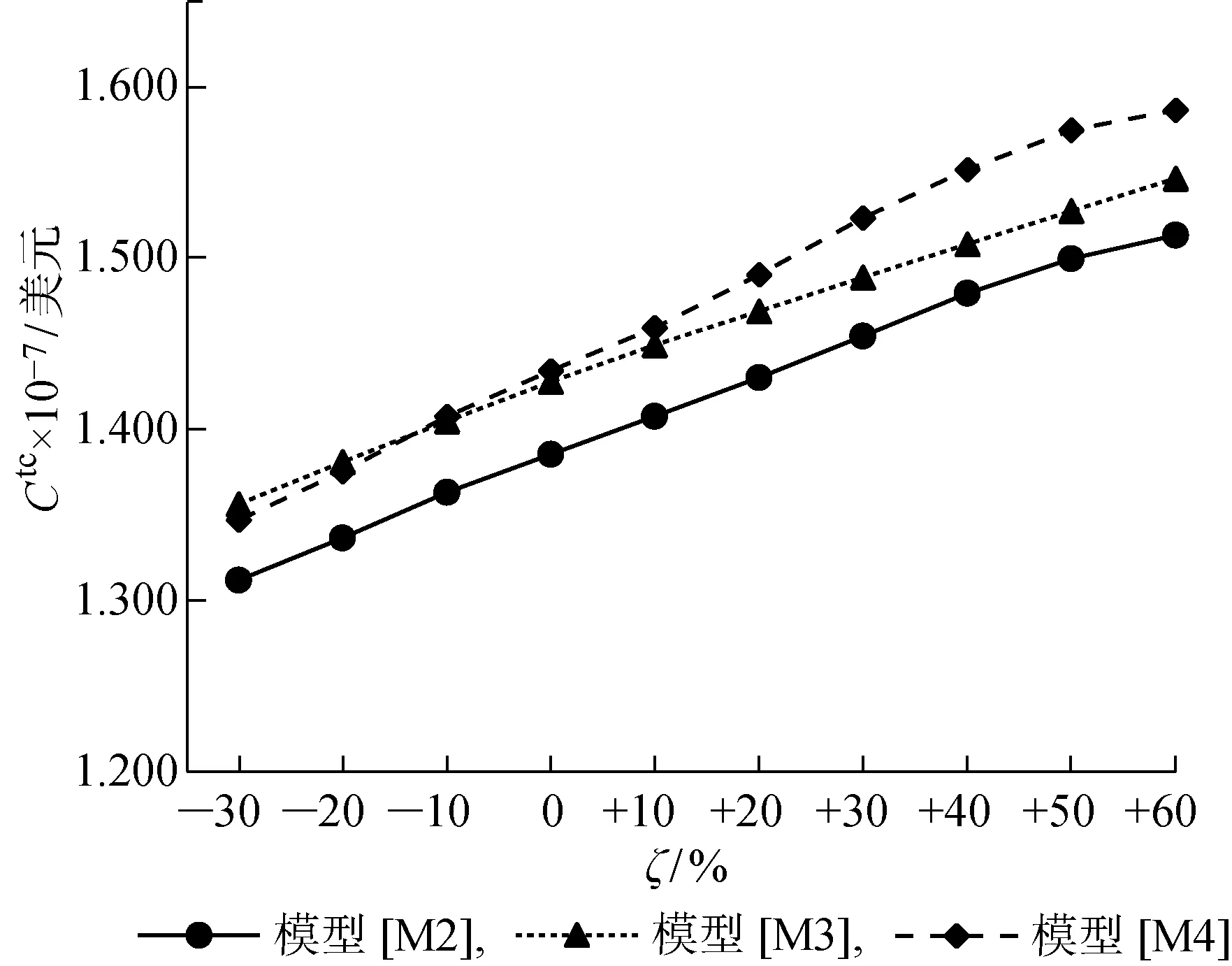
由圖4各模擬場景的總成本平均值可以看出，隨著燃油價格的升高，3種模型得到的船公司周班輪運輸服務總成本都呈增加的趨勢.當燃油價格變化率較低時，模型[M4]得到的總成本低于模型[M3]得到的總成本；當燃油價格變化率較高時，模型[M3]得到的總成本低于模型[M4]得到的總成本.但無論燃油價格怎樣變化，模型[M2]得到的總成本總是最低的.究其原因，是因為當各加油港燃油價格在較低位增加時，盡管燃油成本會有所提高，但船舶到港多時間窗、多起訖時刻和多裝卸速率合作協議能使船公司更加靈活地調整船舶航速，選擇合理的裝卸速率，降低船舶延誤懲罰成本、庫存成本和裝卸成本，從而使得合作協議下不考慮加油策略的模型[M4]得到的總成本低于無合作協議下考慮加油策略模型[M3]得到的總成本；而當各加油港燃油價格處于較高位增加時，燃油成本在班輪運輸服務總成本中的占比必然升高，考慮各加油港燃油價格及其燃油折扣差異的加油策略，可以使船公司選擇合理的加油港和加油量，有效減緩燃油成本的急劇升高，從而使得無合作協議下考慮加油策略模型[M3]得到的燃油成本低于合作協議下不考慮加油策略模型[M4]得到的總成本.合作協議下考慮加油策略的模型[M2]兼具模型[M3]和[M4]的優點，所以不論燃油價格如何變化，本文模型方法都具備明顯的成本優勢.

5 結論

在集裝箱班輪運輸中，設計合理穩定的船期既能較好地滿足客戶集裝箱貨物托運和交付的需求，又是船公司和港口碼頭運營商運營組織優化的需要.本文基于港口碼頭運營商與船公司間簽署的多時間窗、多起訖時刻和多裝卸速率合作協議，構建了班輪運輸船期設計和加油策略聯合優化模型，設計了離散線性化模型求解方法，AEX1航線 1 000 個模擬場景的算例計算結果表明：

(1) 盡管在各模擬場景下得到的船舶到/離各港口時刻及加油量存在明顯差異，但船舶一個往返航次的總時間、航線配船數量和加油港選擇等優化結果均保持不變.

(2) 無論燃油價格如何變化，基于船舶到港多時間窗、多起訖時刻和多裝卸速率合作協議，進行船期設計和加油策略聯合優化所得到的各模擬場景班輪運輸服務總成本最小值、平均值和最大值均低于已有文獻的相對應結果值，平均值可節省3.0%以上.

(3) 在合作協議中的船舶到港時間窗長度越長，越有利于船公司靈活地調整各航段的船舶航速，降低船公司班輪運輸服務總成本.雖然船舶到港時間窗長度并不等同于船舶占用碼頭泊位時間長度，但其長度的增加卻可能會對港口碼頭泊位資源服務其他船公司造成不利的影響，故會給碼頭運營商帶來機會成本損失.因此，確定合理的船舶到港時間窗長度對于船公司與各港口碼頭運營商間簽署共贏的合作協議而言至關重要.

需指出的是，本研究是在假定船公司與各港口碼頭運營商已簽署多時間窗等合作協議前提下開展的，尚未考慮港口服務于多條集裝箱班輪航線下的碼頭泊位時間資源約束因素.如何在考慮港口集裝箱航線間影響及碼頭泊位時間資源約束的條件下，設計船公司與碼頭運營商共贏的合作協議，并據此進行班輪運輸船期設計和加油策略聯合優化，將是一個值得今后深入研究的問題.