基于申威1621數學庫中的非精確結果異常處理①

張天罡,王 磊

(中原工學院 前沿信息技術研究院,鄭州 450007)

CPU 廠商紛紛推出了與自身硬件平臺相對應的數學庫軟件,國產申威芯片同樣需要一個功能完備、性能優越的數學庫軟件. 基礎數學函數庫用以支撐在國產處理器平臺上科學計算方面的應用課題的可靠高效運行,并作為系統核心支持軟件集成到單機編譯器之中. 同時,基礎數學函數庫軟件為基礎語言編譯和優化編程提供支撐. 目前,已經研發了多個面向申威26010眾核處理器[1]深度優化、符合IEEE 754 標準[2]和ISO C99 規范的高效基礎數學函數庫版本,并將其投入到申威1621 多核處理器中使用. 數學函數在浮點運算[3]過程中,會出現浮點異常的情況,如何高效處理則至關重要. 文獻[4,5]充分證明了一個數值計算軟件要達到沒有浮點異常產生的效果,其實現困難程度巨大. 在驗證軟件的可靠性方面,文獻[6–8]提出了測試工具DART,CUTE 等,其中DART 可以對任何編譯的程序進行自動化測試. 文獻[9,10]提出了浮點標準形式化的工具Coq,Gappa 等,文獻[10]提出的Gappa 使用區間算法自動評估和傳播舍入誤差,并且演示了該工具在浮點程序類中的實際使用,即為數學庫中基本函數的實現,遺憾的是缺乏直接針對浮點計算實現的形式化分析方法. Xia 等人[11]依照浮點運算規則計算出了特殊數參與運算后的返回值,從而為浮點數值軟件的異常分析奠定了基石.

文獻[12]提出了一種新的異常處理表示法,該方法能夠以合理的效率同樣很好地滿足故障、結果分類和監控異常的需求. 文獻[13]成功實現應用后,其原理的變化是微乎其微的. 文獻[14,15]對這類與異常領域相關的學術性研究和工程性探索也進行了詳細的對比分析. 文獻[16]對基于IEEE 754 規范下的浮點異常問題進行了深入研究,分析并總結出面向C 語言環境中的不同運算操作的異常產生的條件. 以上的很多研究有一個明顯的局限性,大都基于C++,Java 等面向對象語言實現,缺乏基于面向匯編語言的實現.

此后許瑾晨等人[17]提出了一種分段式異常處理方法,這種方法不僅是面向匯編函數而且是針對浮點運算,恰好彌補了上述研究的局限性. 為了保證方法的高效性,其先進行浮點異常編碼,然后將異常處理過程分為3 個階段,巧妙地將異常處理過程和核心運算分離開來,并應用于申威1621 基礎數學庫. 吳凡[18]在基礎數學庫適配申威1621 的過程中為了解決fcvtdl_z 指令產生的INE 異常問題,提出一種浮點小數取整法,提前將浮點小數轉換為浮點整數,但這種方法有一定的局限性,它只可應用于絕對值大于1 的浮點小數,因此對于像floor 、ceil 、round 等數值函數來說,要保證定義域內所有數據的正確性,就需要用到本文提出的數據集分段處理方法.

申威1621 作為一款高性能的多核處理器,并且具有自主知識產權,近年來已相繼推出了與之對應的國產數學軟件,但是在異常處理方面還并不完善. 而glibc數學庫作為目前最大的開源數學庫,已經形成了一套成熟的功能體系,并且獲得了大多數CPU 廠商的認可.為了使基礎數學庫更好的適配申威1621 芯片,應用于市場用戶的研發以及生態體系的構建,在讓申威數學庫保證功能上的完備性的同時兼顧其高效率,并完全通過glibc 測試集、gcc 工具鏈以及SPEC[19]等市場上主流的測試軟件的測試,需要先將glibc 開源庫移植到申威平臺,再把基礎數學庫集成到glibc 中,并用開源測試數據集對其進行功能測試,最后對其異常處理. 本文將針對申威1621 現有數學庫功能測試出的不精確異常問題從檢測、分析和處理3 個角度詳細展開敘述.

本文主要貢獻:

(1)對主流開源的glibc 測試標準和機制進行理論研究,總結出了一套詳細測試流程,為國產數學庫在不同的架構中進行擴展提供了可能.

(2)提出一種數據集分段式處理的方法,應用于需要消除INE 異常的函數,使基礎數學庫同時符合了IEEE 754 標準和glibc 測試標準,經過算法改進后的函數平均性能加速比達到148%.

為了更加清晰的表述本文問題,第1 節詳細介紹了glibc 的異常檢測機制,總結出一套融合異常檢測的浮點函數算法; 第2 節利用浮點控制寄存器(floatingpoint control register,FPCR)跟蹤定位非精確結果異常(inexact exception,INE)產生的位置并且分析其原因;第3 節提出一種數據集分段處理的思想,對數值函數進行算法改進,高效解決了INE 異常; 第4 節進行正確性測試和性能測試,對比INE 異常在應用此方法前后的區別以及性能的變化情況,以此來說明以上方法的可行性; 第5 節是總結與展望.

1 glibc 異常檢測機制

劉劍[20]提出了一種浮點異常檢測方法,通過詞法與語法來分析源代碼的語義,并利用修改規則模板,對源代碼進行轉化,同時利用狀態標志位記錄其檢測的行號,從而生成含有浮點異常檢測的新程序.以上的過程有一定局限性,它只能通過半自動的代碼轉換程序完成,且只能檢測出異常類型以及出現源碼的位置.

為了更清晰的說明如何檢測出的異常以及后續的處理方法,下面介紹glibc 數學庫的異常檢測機制,該檢測流程在進入具體函數實現之前先將所有異常清除和檢測ULP 是否按照預期的方式進行或者中止; 在經過初始化后正式進入具體函數的測試集進行逐一檢測,針對于某個函數的某個參數先計算其最大能允許的精度誤差; 在正常運算的過程中,通過將調用基礎數學庫計算的值和glibc 給出的期望值進行一系列對比,從而完成異常類型、異常錯誤碼以及計算精度問題的檢測.最后對檢測結果總數進行統計,輸出異常和errno 的測試數量. 其基本流程如圖1 所示.

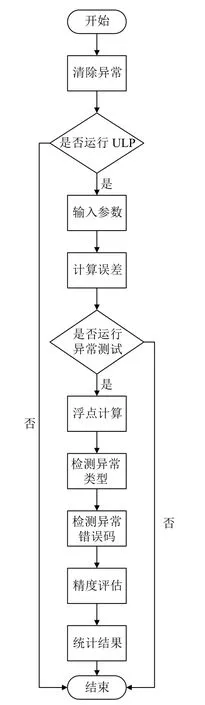
圖1 glibc 數學庫異常測試機制

本文研究的異常檢測機制相比于現有的異常檢測機制,它的創新性在于可以在全自動的程序中快速完成,并且檢測到的異常信息更加全面,主要異常信息包括異常類型、異常錯誤碼以及異常返回值,其基本算法如算法1 所示. 該算法在初始化后對不同異常的類型,不同異常的錯誤碼以及計算精度結果進行檢測.check_ULP 函數驗證ulp()實現是否按預期運行或中止; enable_test 函數根據異常標記參數判斷是否需要進行接下來的一系列的異常測試; check_exception、check_errno、ulpdiff 三個函數都是將實際值和glibc 期望的值進行比較,如果不同則返回相應的異常類型、異常錯誤碼以及誤差范圍; COUNT_ARRAY 為測試集的個數,EXCEPTIONS 為異常標記參數,Computed為實際的值,expected 為glibc 期望的值.

算法1. Exception detection 1. TEST_INIT;//清除異常位的設置2. if check_ULP()≠ 0 then 3. for 1…COUNT_ARRAY do 4. if enabe_test(EXCEPTIONS)≠0 then 5. if check_exception(computed,expected)=true then 6. return E; //返回異常類型7. end if 8. if check_errno(computed,expected)=true then 9. return E; //返回異常錯誤碼10. end if 11. if ulpdiff (computed,expected)=true then 12. return ULP;//返回誤差范圍13. end if 14. end if 15. end for 16. end if 17. TEST_FINISH;//統計檢測結果

2 FPCR 寄存器分析法

glibc 異常檢測機制可以較全面的檢測出程序中的INE 異常,為了更好的處理這些異常,本文提出了基于FPCR 寄存器的分析方法,對觸發異常的指令和算法進行了詳細分析. gdb 作為調試工具,它可以在程序中追蹤查看變量、寄存器、內存及堆棧,更進一步甚至可以修改變量及內存值. 因此,我們在進行浮點運算時,可以依托這樣功能強大的調試器,在不同的舍入模式下,對比FPCR 寄存器第56 位值的變化,從而定位到程序中INE 異常的觸發位置. 經過以上分析,我們可以將觸發的INE 異常分為以下兩類:

(1)指令觸發

fcvtdl_n $f16,$f11 //觸發INE 異常

以floor 函數為例,fcvtdl_n 指令將D-浮點數轉化成長字,結果負無窮舍入,在完成向下取整功能的同時也觸發了INE 異常.

(2)算法觸發

faddd $f16,$f1,$f10 //觸發INE 異常

以ceil 函數為例,faddd 指令計算的結果舍去了小數位,造成了結果的不精確表示. 表1 例舉了特殊數4 503 599 627 370 496 前后部分浮點格式的16 進制和10 進制的數據對應關系,發現一個規律,以浮點數0x4330000000000000 為分界點,對于此浮點數的浮點格式有效位每加1,其10 進制也就加1,比如0.5 加上4 503 599 627 370 496 本該等于4 503 599 627 370 496.5,但浮點格式的有效位已經無法表示如此精確的計算結果,自動將其近似4 503 599 627 370 497,這樣就實現了函數ceil 向上取整的功能,同理原算法中任何一個小數加上這樣一個特殊數,浮點格式的有效位就不足以容納精確的計算結果,從而觸發INE 異常. 后面第4 節將以round函數為例,進一步分析這種由本身算法設計帶來的INE 異常,并提出一種數據集分段處理方法將對現有算法進行改進,以達到消除這種INE 異常的目的.

表1 IEEE 754 數據轉換

3 數據集分段處理

數據集分段處理的核心就是首先進行輸入參數檢測,如果遇到無窮、非數等異常數直接處理并結束程序; 如果檢測到的是浮點有限數,則根據數據集不同的定義域區間分別處理并返回.

依據 IEEE-754 的規范標準,在十進制數運算的四舍五入中,round函數的使用功能介紹為根據四舍五入取整數原則選擇最貼近x的整數. 在申威1621 處理器現有的基礎數學庫中,round函數現有算法流程圖如圖2 所示.

圖2 round 函數現有算法流程圖

現有round函數的算法都是先判斷輸入值是否大于特殊數4 503 599 627 370 496,大于這個特殊數的值寄存器會根據默認的舍入模式進行舍入,因此直接返回即可. 小于這個特殊數的輸入值,會經過加值、修改舍入模式、截斷舍入3 步完成函數的功能.

Step 1. 加值

在輸入值的基礎上加上一個值的大小為0.5 的數,其符號位與輸入值的符號位保持一致.

Step 2. 修改舍入模式

先用rfpcr 指令讀取浮點舍入模式的狀態標志位,然后通過移位、與非等邏輯操作修改浮點舍入模式的狀態標志位,最后用wfpcr 指令將其寫回,從而將四舍五入改為向0 舍入.

Step 3. 截斷舍入

通過加上特殊數4 503 599 627 370 496,舍去小數位.

經過以上3 步,原本是1.0–1.4 的小數加上0.5 再截斷舍入就為1,1.5–1.9 的小數加上0.5 再截斷舍入則為2,從而實現了小數域四舍五入的功能. 然而,在第3 步截斷舍入時,用faddd 指令舍去小數位的同時,也造成了計算結果的不精確表示,引發了INE 異常,下面運用數據集分段處理的思想,詳細闡述如何消除此處的INE 異常. 改進后round 函數算法流程如圖3 所示.

圖3 相比于現有的算法,利用申威1621 處理器的硬件特性,首先通過以下代碼段對異常數檢測并處理,然后根據數據集不同的定義域區間分別處理并返回.

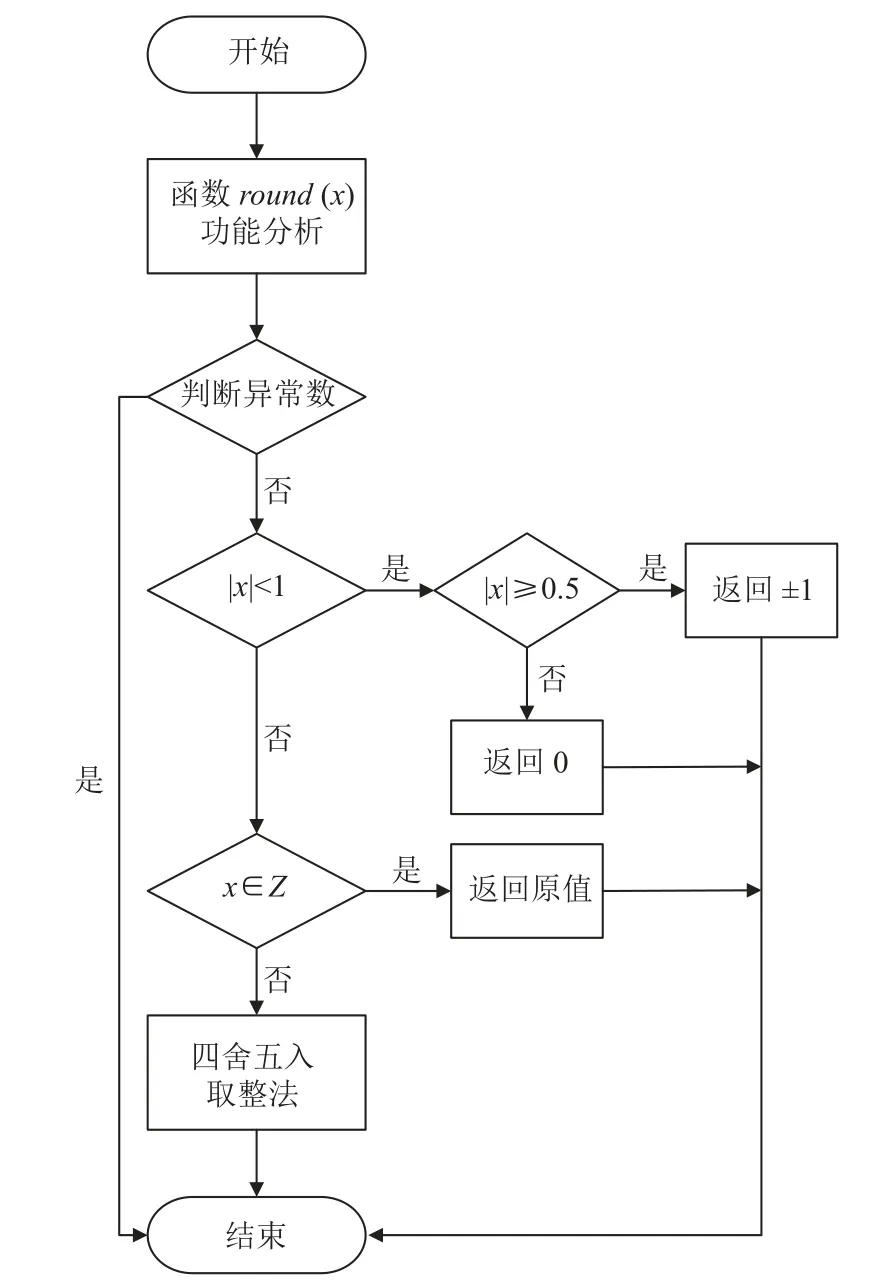
圖3 改進后round 函數算法流程

對于絕對值小于的1 的浮點小數來說,四舍五入的實現主要和指數有關,若浮點數的指數減去1 023 的十進制值是–1,那么浮點小數的絕對值應為[0.5,1),若浮點數的指數減去1 023 的十進制值小于–1,那么浮點小數的絕對值應為[0,0.5).

數值大于 1 的浮點數,整數和小數位共同構建了浮點數的尾數位，其中構成浮點數整數部分的位數和浮點數的指數位密切相關. 從雙精度浮點數的數據類型不難得出,如果浮點數的指數位減去值為1 023 后的數表示為x,那么小數部分占用尾數的 0～(51–x)位,尾數(51–x)+1～51 則用來表示整數. 如果將小數點后的所有數字都更改為零,則會得到小數點后的整數. 同樣相對于絕對值大于1 的二進制數字而言,將小數點后面的位全部置為 0,也就是將雙精度浮點數的[0,51–x]位置0,則該二進制浮點數就變成了一個浮點整數[18].

下面重點介紹round函數數據集分段處理中所使用的整數判斷法和四舍五入取整法的具體步驟.

3.1 整數判斷法

假設是對雙精度浮點數f1 進行整數位的判斷:

Step 1. 將f1 傳進二進制數t1; 再將t1 右移52 位得到t0;生成一個十進制值為2 047 的t2,將t2 與t0 相與得到f1 指數位的十進制值x1.

Step 2. 將x1 和十進制為 1 023 的值相減,計算出浮點數的尾數部分整數占據的位數n.

Step 3. 構造符號位、指數位全0,尾數位全1 的二進制數t3; 再將其右移n位,得到尾數位表示整數位

Step 4. 將t3 和t1 進行邏輯與操作; 如果浮點數f1是整數,那么二進制t1 表示小數的位上應為全0,與操作后得到數也應為全0; 反之,則判斷浮點數f1 不為整數.

3.2 四舍五入取整法

以上算法中浮點小數根據四舍五入原則取最接近x整數的具體步驟如下.

如果遵循四舍五入的原則進行取整的是雙精度浮點小數f1:

Step 1. 取得f1 的指數e1,取得浮點數1 的指數e2; 然后將e1–e2 得到的十進制數值用n表示,從而計算出浮點數的整數部分所占的位數.

Step 2. 構造符號位、指數位全0,尾數位全1 的二進制數t2; 再將t2 右移n位,計算出表示浮點數的整數位上全0 的二進制t3.

Step 3. 構造浮點最小值f2,將其對應的二進制數右移n位得到t4; 接著將t4 加上t1 得到二進制數t1,完成了四舍五入前的加值操作.

Step 4. 將表示浮點數整數位上全0 的二進制t3 按位取反,得到表示小數位上全0 的二進制數t3.

Step 5. 將二進制數t3 與t1 相與,得到的二進制數傳給f1,從而完成了浮點小數f1 的四舍五入.

其他數值函數floor,ceil,nearbyint,nextafter,算法改進的方法和round函數類似. 用開源測試數據集測試的INE 異常不需要設置的所有函數,通過這樣的算法改進,完全可以消除INE 異常.

4 測試結果及分析

為了更直觀地驗證本文采用的數據集分段處理方法的可行性,將測試平臺選為申威 1621 處理器,表2詳盡的例舉出了處理器相關配置信息.

表2 申威1621 實驗平臺

浮點計算程序的正確性和性能都得到了驗證. 正確性測試根據 glibc 異常檢測機制,將異常處理前后的計算結果進行比較; 性能測試分別對異常處理前和異常處理后的測試結果進行對比,并求得經過算法改進后的函數平均加速比.

注意這里性能加速比的計算公式和其他文獻計算的方式不同,具體如下:

性能加速比=(算法改進前節拍/算法改進后節拍)×100%

4.1 正確性測試

在驗證glibc-2.28 libm 和基礎數學庫函數功能是否一致的過程中,用開源測試數據集測試出基礎函數庫中INE 異常需要消除的函數,圖4 以double 類型為例,例舉了5 個不同函數INE 異常需要消除的測試集個數,橫坐標表示了函數名稱,縱坐標表示引發INE 異常的測試集的數目.

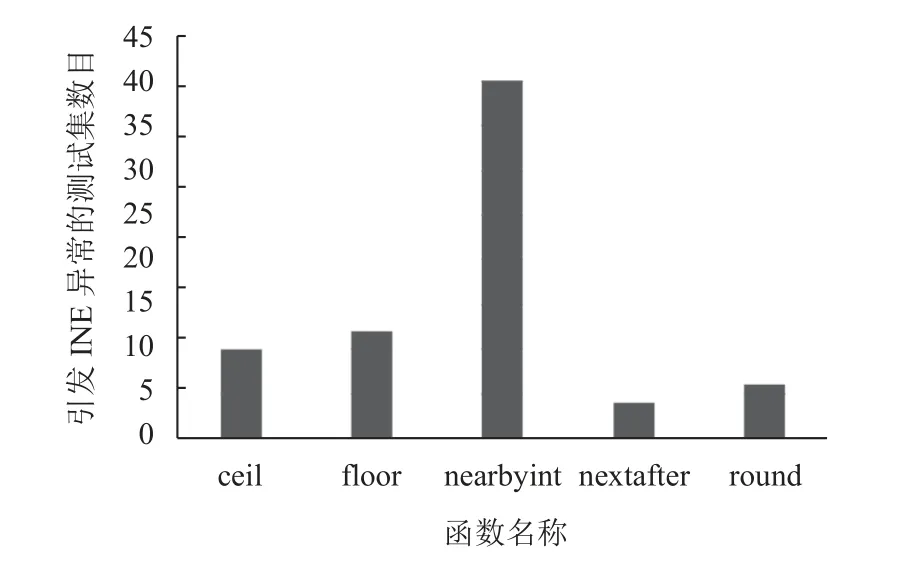
圖4 INE 異常測試集統計

從圖4 中不難發現,INE 異常需要消除的函數全部集中在數值函數中,通過應用以上數據集分段處理的方法,再進行測試則發現將圖4 檢測到的5 個函數不同測試集的所有INE 異常消除.

4.2 性能測試

申威1621 處理器整數部件中有一個控制狀態寄存器TC,作為周期計數器. rpcc 指令作為如今超級計算機衡量性能的通用計時指令,通過插樁采樣來計算被測函數的運算節拍數來判斷性能的高低. 為了保證性能測量結果能夠涵蓋所有被測函數的熱點路徑,首先進行熱點分析,并檢查數據集主要使用的是隨機浮點數,其特點為都在0–1 區間范圍內均勻分布,以測試基礎數學庫中運行上百次以上的總節拍數[18]. 為了排除誤差較大的測試數據對性能測試結果的干擾,采用4D 檢測法[21]對測試結果數據進行相關處理,從而求得算術平均值. 測試結果如圖5 所示,橫坐標表示函數名稱,縱坐標表示函數運行節拍數.

圖5 算法改進前后性能對比

從圖5 的性能測試結果來看,除了ceil,ceilf 以外函數的性能還是有所提升的,并且可以算出平均加速比為148%,以此證明了這種方法的高效性. floor 函數性能提升的效果最為明顯,加速比達到了213.75%,floor 函數原來算法中相比于別的同類數值函數多了一條 SETFPEC0 指令,這個指令會導致流水線中斷,嚴重降低函數性能,因此算法改進前運行節拍數就達到了171 cycles,節拍數遠遠大于其他同類數值函數,從而使得性能提升最為明顯; ceilf 函數算法改進前由于不存在任何斷流水的指令,運行節拍數就為66 cycles,屬于同類函數中節拍數最小,經過數據集分段處理后,判斷分支明顯增多,導致性能加速比為75%,相比于異常處理前性能有一定的下降.

綜合正確性測試和性能測試的測試結果分析,可以得出數據集分段處理的方法,在保證了功能的前提下還兼顧了性能,足以說明這種方法的有效性.

5 總結與展望

本文提出一種數據集分段處理的方法,并應用于floor、ceil、trunc、round 等8 個數值函數,同時以round函數為例進行算法改進,歸納出其中用到的整數判斷法和四舍五入取整法. 測試結果表明,此方法消除了所有INE 異常,且相對于算法改進前平均性能加速比達到了148%. 下一步,我們將試圖從理論檢驗的視角全面證實本文方法的可行性,并且把以上異常處理方式推廣至更多的浮點運算型數值軟件系統之中.