指數Gamma分布在無資料地區水文頻率分析中的應用研究
李 航,易瑞來,廖樸訥
(廣州市增城區中新鎮人民政府,廣州 511365)
1 概述
隨著我國水利事業的蓬勃發展,目前國內水利工程的建設重心已經從大型水利工程向中小型水利工程轉移,而城市化進程的飛速推進、城市防洪排澇體系的不完善和城市布局的不合理,越發凸顯城市中小型水利工程配套建設的落后。水文頻率分析是根據區域內的某種水文現象的統計特征,利用現有水文數據資料,分析和計算水文變量設計值與重現期之間的定量關系,是水利工程規劃、設計與管理的基礎和科學依據,分析結果的精確與否將會直接關系到流域水利工程是否能夠發揮其應有的作用[1]。然而,中小流域作為近年來水利工程的建設重心,常常會因為自然條件和人為因素的限制,出現無法取得基礎性水文數據的狀況,為水資源的科學管理和水利工程的規劃建設造成很大困擾。根據世界氣象組織的統計數據,最近20年間,世界上的水文站點數量正在迅速減少,尤其是前蘇聯和一些發展中國家,作為最大的發展中國家,中國現有的設站條件面臨著同樣的難題[2]。
為解決無資料地區的水文頻率分析和水文預報問題,促進水文科學理論研究和技術研究應用于解決實際性問題,2003年7月國際水文科學學會(IAHS)正式啟動無資料地區水文預測計劃,即PUB計劃(Prediction in Ungauged Basins)[3]。經過十幾年的研究對比,目前常用的無資料地區水文頻率分析和水文預報的方法可以大致分為四類:隨機模擬法[4-6]、區域化方法[7-8]、徑流系數法[9-10]和參數等值線圖法[11],分別適用于不同資料缺失程度的研究區域。在工程所在流域找不到參證流域且無降雨資料的情況下,參數等值線圖可以根據已繪制的各省市水文特征等值線圖經過計算得到設計年徑流量[12]。因此,參數等值線圖法成為中小流域水利工程建設過程中實際應用最多的方法。
目前,參數等值線圖法中最為常用的水文頻率計算模型為皮爾遜Ⅲ型分布。然而,皮爾遜Ⅲ型分布并不能適用于各種自然條件,且近年來隨著水文極值的不斷出現[13],在水文頻率分析過程中時常出現皮爾遜Ⅲ型分布與經驗點據明顯脫離的不合理現象[14]。為了提高水文頻率分析模型的適用性和彈性,同時兼容現有皮爾遜Ⅲ型分布的設計標準,1985年,中國水利水電科學研究院孫濟良先生等[15]提出指數Gamma分布模型,該模型可以通過改變參數轉化為包括P-Ⅲ型分布、對數正態分布在內的10余種常見分布模型。
受限于當時的計算機技術及模型計算方法,具有4個參數的指數Gamma分布參數估計計算較為復雜,因此并沒有得到廣泛的應用。隨著計算機的廣泛應用和模型方法的研究,指數Gamma分布優秀的擬合效果和適用性得到越來越多水文學者的關注。
在我國現有條件下,基層水文工作缺乏足夠技術力量支持,水文測站無法短時間內在全國范圍內普及。在缺少技術力量和水文資料的情況下,將指數Gamma分布應用于參數等值線圖法,并開發配套的水文設計值計算工具,能夠免去篩選合適擬合曲線的繁瑣過程,有效解決各種水文自然條件下無資料地區的水文頻率分析問題,并提高水文設計值計算精度。
本文選取江谷河流域作為研究區域,以指數Gamma分布作為頻率分布曲線,通過廣東省水文局頒布的《廣東省暴雨參數等值線圖》(2003年版)采用參數等值線圖法進行水文頻率分析,得出暴雨設計值與采用優化適線法的指數Gamma分布計算結果和采用參數等值線圖法的P-Ⅲ型分布計算結果進行對比研究,分析指數Gamma分布在無資料地區的水文頻率分析結果的可靠性。文中分析結果以期為我國無資料地區水文頻率分析的研究和應用提供支撐。
2 指數Gamma分布的參數估計方法
設隨機變量X服從指數Gamma分布,其概率密度函數為:
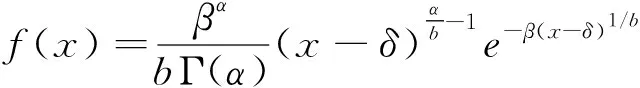
(1)
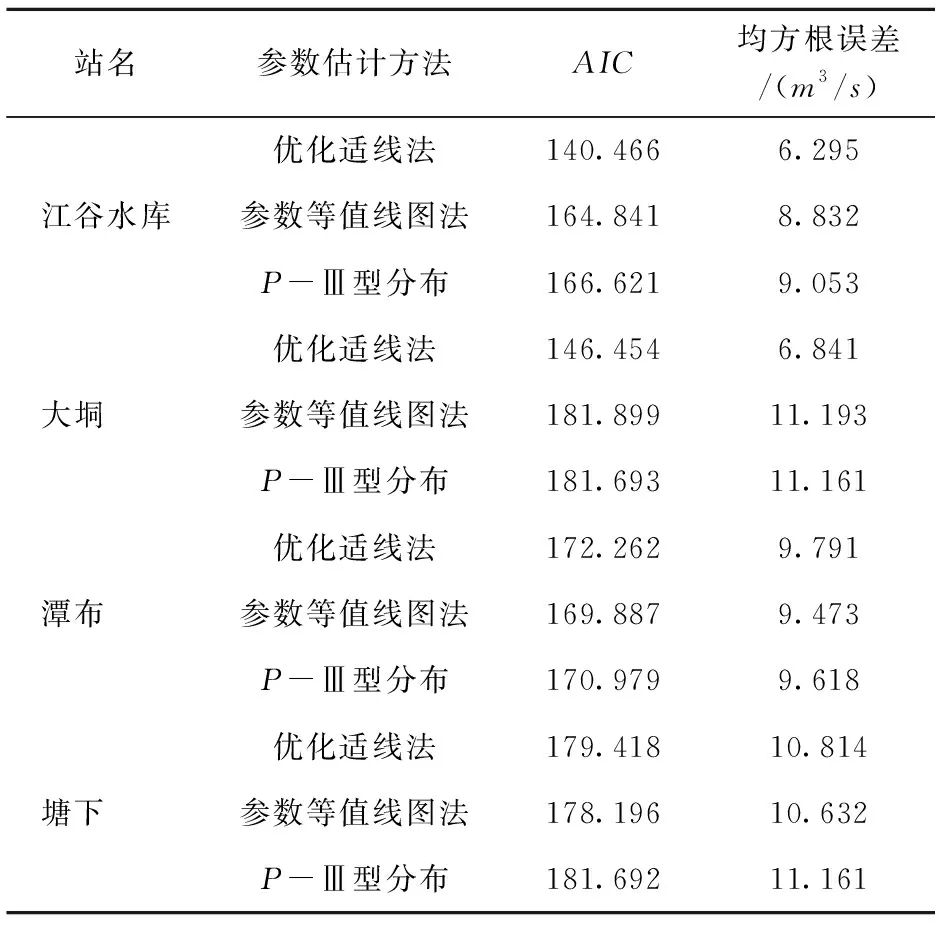
α>0,β>0,δ 式中: α,b,β,δ——分別為指數Gamma分布的形狀參數、變換參數、比例參數和位置參數。 變換參數b的取值范圍一般為0≤b≤10,其中位置參數δ為模型隨機變量X的下限,同時也為保證隨機變量X不會出現負值的情況,在某一研究區域的頻率分布模型中,δ表示為隨機變量X在該研究區域的最小值。將指數Gamma分布采用積分法進行積分,可以得到指數Gamma分布的超越概率分布函數F(x)。在水文頻率分析中,通常使用超越累計頻率P代表F(x),即: (2) (3) (4) (5) (6) 式中: v1——一階原點矩; μ2——二階中心矩; μ3——三階中心矩; μ4——四階中心矩。 其中: (7) (8) μ3=[Γ2(α)Γ(α+3b)-3Γ(α+b)Γ(α+2b)+2Γ3(α+b)]/β3bΓ3(α) (9) μ4=[Γ3(α)Γ(α+4b)-4Γ2(α)Γ(α+b)Γ(α+3b)+6Γ(α)Γ2(α+b)Γ(α+2b)-3Γ4(α+b)]/[β4bΓ4(α)] (10) 應用矩法,可以得到指數Gamma分布設計值的計算公式[1]: (11) 式中: (12) 離差絕對值和最小準則為: (13) 式中: xi——經驗頻率Pi下的水文實測值; xi*——相應頻率下估計值。 以α、b、β、δ作為未知參數,選用離差絕對值和最小準則作為目標函數求解各參數值。 設樣本序列長度為n,將樣本序列按降序排列為xi(i= 1, 2,…,n),頻率計算公式為: (14) (15) (16) (17) (18) 查閱《廣東省暴雨參數等值線圖》(2003年版),獲取江谷水庫、大垌、潭布、塘下的水文頻率特征參數,分別以指數Gamma分布和P-Ⅲ型分布作為頻率分布曲線,采用參數等值線圖法進行水文頻率分析。選取江谷水庫、大垌、潭布、塘下4個水文測站的年最大3 d暴雨實測序列,以指數Gamma分布作為頻率分布曲線,采用優化適線法進行水文頻率分析。對比基于指數Gamma分布的參數等值線圖法分析結果與其余兩種方法的擬合情況,分析指數Gamma分布在無資料地區水文頻率分析的適用性。本文所選暴雨資料通過了“三性審查”,符合水文頻率計算的要求,研究區域的水文資料系列長度見表1所示。 表1 暴雨資料系列長度 表2 各站點指數Gamma分布參數估計結果 本文選取4個雨量站的年最大3 d暴雨實測序列作為研究對象,對比分析2種參數估計方法下指數Gamma分布和參數等值線圖法下P-Ⅲ型分布對經驗點據的擬合情況,擬合情況如圖1所示。由圖1可知,優化適線法、參數等值線圖法和P-Ⅲ型分布確定的頻率曲線均能夠很好的擬合經驗點距的各個部分,且表現穩定。其中,優化適線法確定的頻率曲線對經驗點距的上部和中部具有更好的擬合效果,2種分布曲線的參數等值線圖法擬合效果次之;而對于經驗點距的下部,2種分布曲線的參數等值線圖法表現出更好的擬合效果。 a 江谷水庫 b 大垌 c 潭布 d 塘下 采用AIC準則和均方根誤差為評價標準,進一步對比分析指數Gamma分布2種參數估計方法與P-Ⅲ型分布的擬合效果,計算結果見表3所示。 綜合表3與圖1的對比分析結果可以得出,4個雨量站暴雨頻率分析中,指數Gamma分布2種參數估計方法計算結果的AIC指數和均方根誤差普遍較小。指數Gamma分布2種參數估計方法中,部分站點優化適線法的結果明顯優于參數等值線圖法,這與參數等值線圖精度不足,參數只能取大概數值有關。作為無資料地區的暴雨頻率分析方法,參數等值線圖法的結果雖然部分站點不如由暴雨實測序列計算出的結果,但其結果仍具有很大參考價值,甚至在取值準確的情況下,結果還要優于優化適線法。 表3 指數Gamma分布設計值誤差比較 本文以江谷水庫、大垌、潭布和塘下4個雨量站的年最大3d暴雨資料為例,將基于指數Gamma分布的參數等值線圖法應用于無資料地區的暴雨頻率分析,并對優化適線法、參數等值線圖法和基于P-Ⅲ型分布的參數等值線圖法進行了頻率曲線的擬合效果評價與誤差分析,評價分析結果如下: 1) 優化適線法、參數等值線圖法和基于P-Ⅲ型分布的參數等值線圖法均能夠很好地擬合經驗點據各個部分,且指數Gamma分布2種參數估計方法計算結果的AIC指數和均方根誤差普遍較小。表明在暴雨頻率分析中,基于指數Gamma分布的參數等值線圖法是一種可選的參數估計方法。 2) 對比優化適線法,參數等值線圖法確定的頻率曲線能夠更好的擬合經驗點距的下部,更適合做為小頻率水文設計值的計算方法,能夠很好的擬合經驗點據的上部。 3) 文中研究了無資料地區基于參數等值線圖法指數Gamma分布的頻率計算。對于隨機模擬法、區域化方法和徑流系數法在指數Gamma分布上的應用有待進一步研究。2.1 矩法
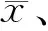
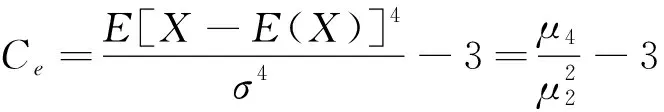
2.2 優化適線法
2.3 參數等值線圖法
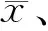
2.4 指數Gamma分布樣本矩的計算
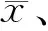
3 應用實例
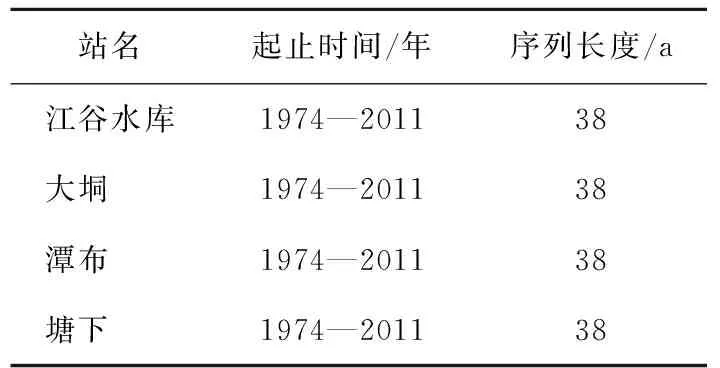
3.1 參數估計及曲線擬合

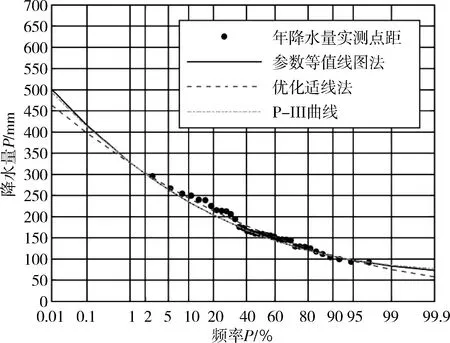
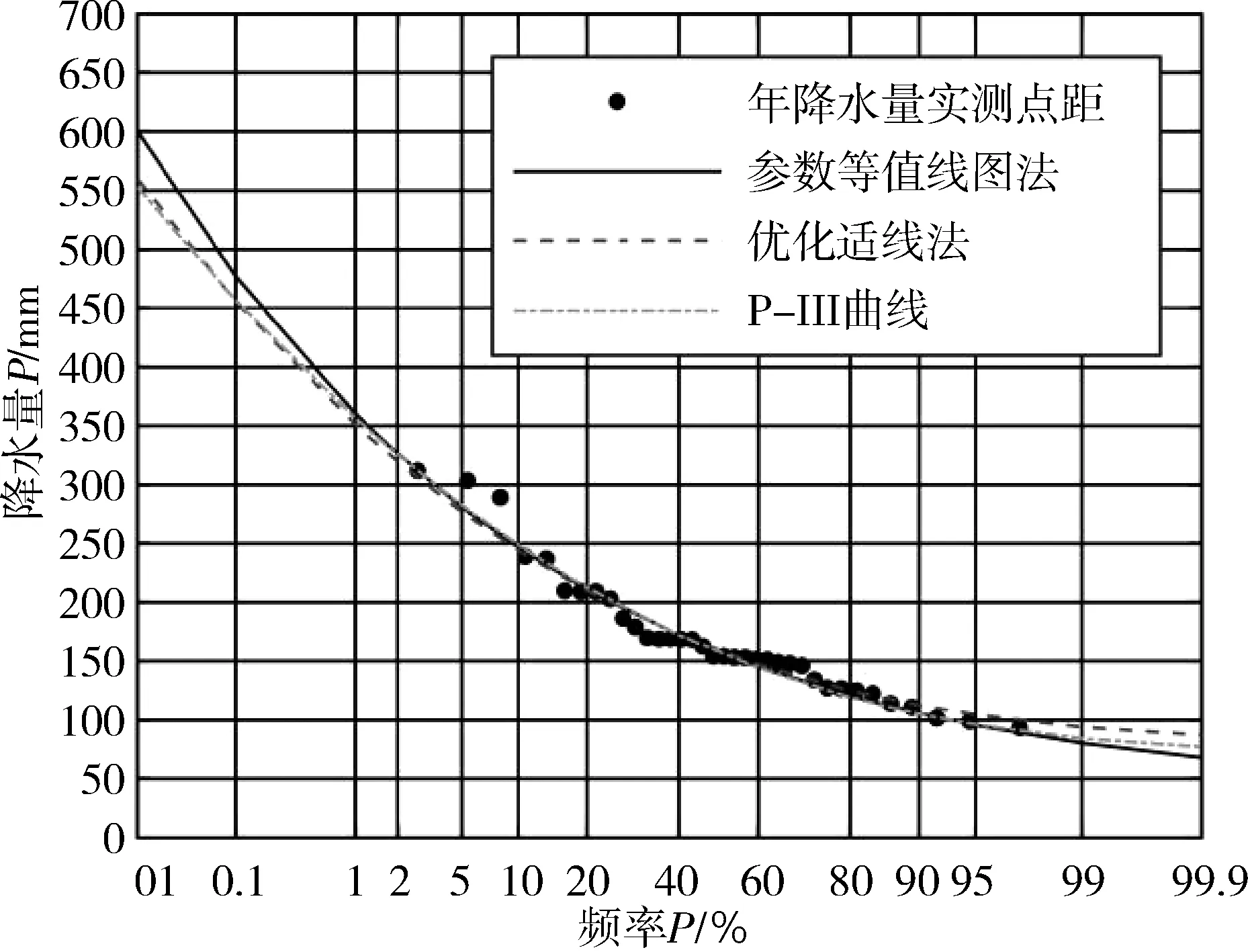
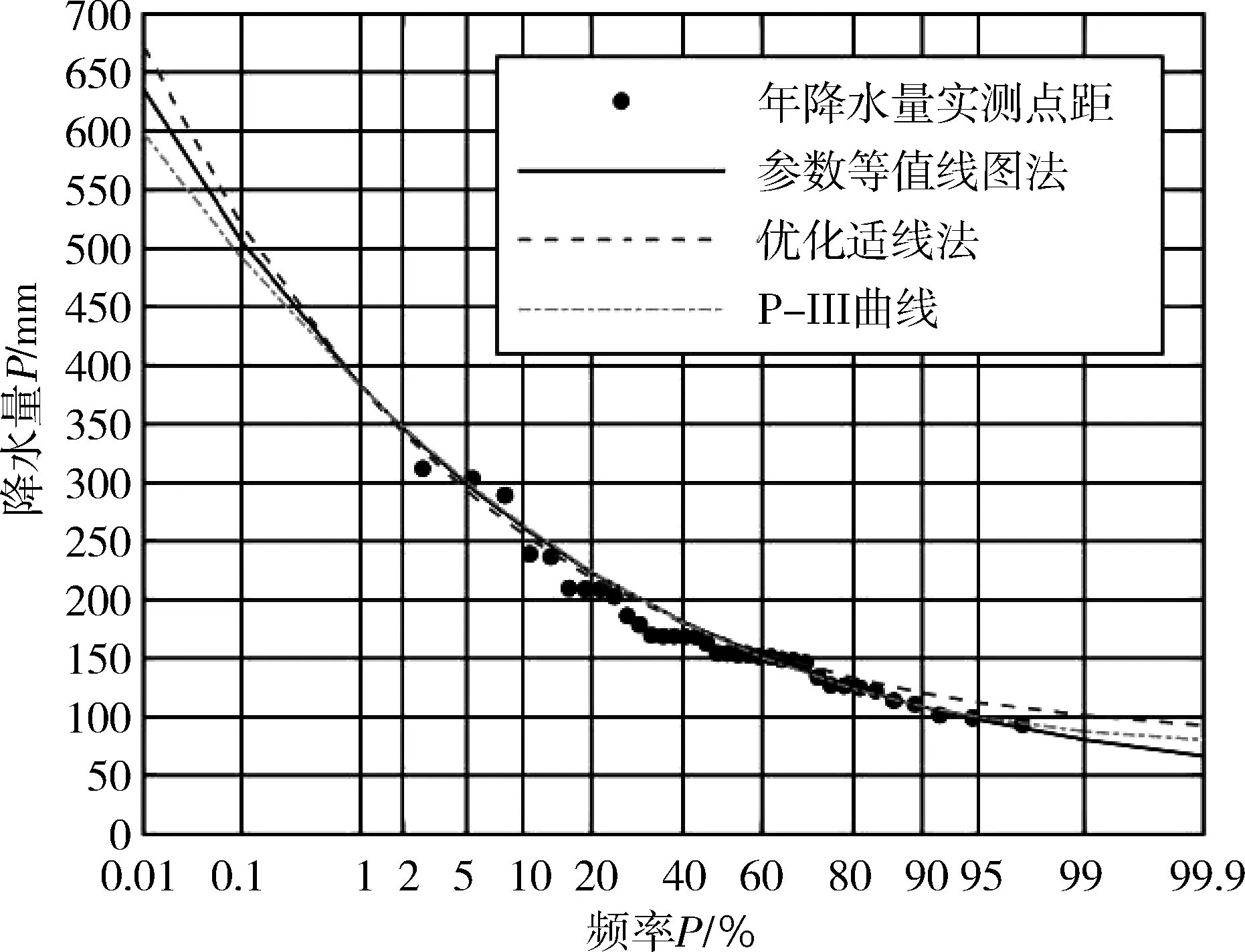
3.2 誤差分析
4 結語

