基于多頭注意力機制和卷積模型的超短期風電功率預測

李俊卿，胡曉東，秦靜茹，張承志

（華北電力大學 電力工程系，河北 保定 071003）

0 引言

隨著“碳達峰”和“碳中和”目標的提出，風力發(fā)電逐漸呈現(xiàn)出高增長的發(fā)展趨勢[1,2]。截至2020年底，我國風電并網(wǎng)裝機容量達到2.8153×1011W[3]。

由于風電具有較強的隨機性，風電的大規(guī)模入網(wǎng)勢必會影響電網(wǎng)的安全穩(wěn)定運行[4,5]。準確的風電功率預測，可以降低電網(wǎng)備用容量和運行成本，有利于電網(wǎng)調(diào)度部門及時準確調(diào)整運行計劃，避免大量棄風[6]。

按照時間尺度來劃分，風電功率預測主要分為長期預測、短期預測和超短期預測[7]；按照預測方法來分，主要包括物理建模方法和統(tǒng)計方法。

物理建模方法主要通過建立數(shù)學模型來研究氣象的演變，根據(jù)風電轉(zhuǎn)換模型進行預測。此種方法模型復雜、計算量大、抗干擾能力弱[8]。

諸如支持向量機（SVM）[9]、BP 神經(jīng)網(wǎng)絡[10]等統(tǒng)計方法已經(jīng)在風電功率預測方面得到了廣泛應用。由于風電功率的預測與當前和歷史數(shù)據(jù)相關(guān)，而傳統(tǒng)的機器學習模型難以處理長時間序列的數(shù)據(jù)，并且存在梯度爆炸、梯度消失等問題，所以其預測的效果尚有待提高。

近年來，深度學習方法因其強大的特征提取和擬合能力在包括風電功率預測的諸多領(lǐng)域得到了廣泛應用[11,12]。常見的深度學習模型主要有卷積神經(jīng)網(wǎng)絡（convolutional neural networks，CNN）、循環(huán)神經(jīng)網(wǎng)絡（recurrent neural network，RNN）、長短期記憶網(wǎng)絡（long-short-term memory，LSTM）等。文獻[13]針對風電功率的預測提出了一種多尺度隱馬爾可夫-RNN 模型，并取得了一定的效果；但是RNN 在處理較遠時間序列時會產(chǎn)生梯度消失的問題，這將導致預測效果不佳。為解決傳統(tǒng)RNN 所存在的問題，文獻[14]考慮利用CNN 強大的特征提取能力，采用GRU 模型，建立了CNN-GRU 預測模型，取得了較高的預測精度；相比于LSTM，此模型大大縮短了預測時間。文獻[15]將卷積神經(jīng)網(wǎng)絡CNN 應用于區(qū)域風電功率的預測，在一定程度上取得了良好的效果；但是，卷積神經(jīng)網(wǎng)絡的池化層會造成大量有價值的信息流失，并且會忽略整體和局部之間的關(guān)聯(lián)性，這導致了預測結(jié)果不夠準確。多頭注意力機制（multi-head attention）算法能夠捕獲序列中的重要信息，并且能夠?qū)崿F(xiàn)并行計算。該算法已經(jīng)在機器翻譯[16]、文字識別[17]等領(lǐng)域得到了廣泛應用。

本文提出超短期風電功率預測建模方法：先利用皮爾遜相關(guān)系數(shù)（Pearson correlation coefficient，PCC）從原始數(shù)據(jù)中挑選出與風電功率相關(guān)性程度高的特征；然后，將經(jīng)過相關(guān)性分析之后的數(shù)據(jù)輸入到多頭注意力機制和CNN 中進行訓練，從而獲得高精度的風電功率預測模型。

1 模型原理

1.1 皮爾遜相關(guān)系數(shù)

用皮爾遜相關(guān)系數(shù)衡量X與Y這2 個變量的相關(guān)程度[18]，其計算公式為：

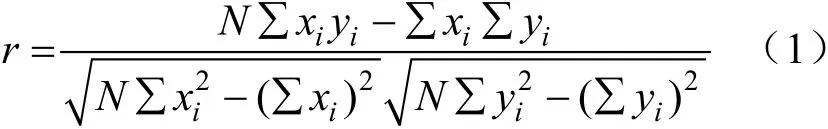
式中：r為X與Y的相關(guān)性系數(shù)；N為樣本數(shù)。

相關(guān)系數(shù)越接近于-1 或1，則相關(guān)度越強；相關(guān)系數(shù)越接近0，則相關(guān)度越弱。

相關(guān)程度與相關(guān)系數(shù)的對應關(guān)系如表1所示。

表1 相關(guān)系數(shù)和相關(guān)程度對應關(guān)系Tab. 1 Correspondence between correlation coefficient and degree of correlation

1.2 多頭注意力機制

注意力機制模擬了人腦注意力的資源分配機制：通過概率分配的方式，對序列中的重要信息賦予足夠的關(guān)注，從而突出重要信息，減少甚至完全忽略不重要的信息[19]。

自注意力公式為：

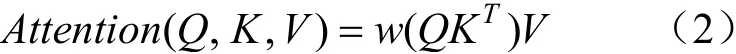
式中：Attention(Q，K，V)為得到的注意力的值；Q、K、V分別為查詢量（query）、鍵（key）和值（value）。

自注意力中，Q、K、V通常通過將序列X分別乘以WQ、WK、WV得到。可以認為，查詢Q是輸入樣本的特征，鍵K是信息的特征、值V是信息的內(nèi)容。

多頭注意力機制是注意力機制的一個變體。與單獨使用一個注意力不同，多頭注意力機制可以獨立學習得到H組不同的線性投影來變換查詢（query）、鍵（key）和值（value）。變換后的查詢、鍵和值并行地進入注意力層，然后將H個注意力層的輸出拼接起來，最后通過一個線性層得到最終輸出。

多頭注意力與單頭自注意力的區(qū)別在于：多頭是復制多個單頭，但權(quán)重系數(shù)不同，類似于單個神經(jīng)網(wǎng)絡模型與多個同樣的網(wǎng)絡模型堆疊。由于初始化不同，其權(quán)重也勢必有所差異。

給定查詢Q∈R、鍵K∈R以及值V∈R，每個頭hi(i=1,···,H)的計算方法為：

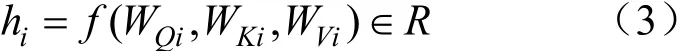
多頭注意力機制函數(shù)為：

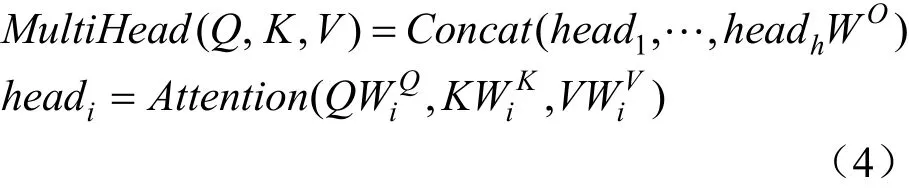
式中：WO為最后一層全連接層的權(quán)重。

在多頭注意力機制中，本文采用的是縮放點積注意力。點積操作要求查詢和鍵具有相同長度。假設查詢和鍵都是相互獨立的隨機變量，且均值為0、方差為1，則這2 個向量點積均值為0，方差與鍵長度一致。假設Q、K、V∈R，則縮放點積注意力為：

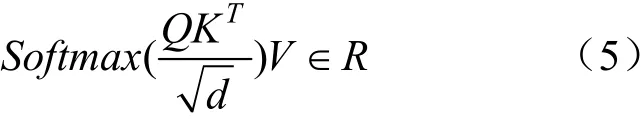
式中：Softmax函數(shù)用于對注意力得分做歸一化處理，以得到的每個鍵的權(quán)重。

1.3 CNN

CNN 主要包括輸入層、卷積層、池化層、全鏈接層和輸出層。卷積層中存在很多卷積單元，即卷積核。每個卷積單元的參數(shù)都通過反向傳播算法不斷優(yōu)化得到。卷積核通過有規(guī)律地“掃描”提取特征，然后經(jīng)過激活函數(shù)的作用來增強非線性的擬合能力，即：

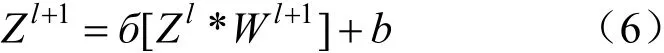
式中：“*”表示卷積運算；b為偏差量；Zl和Zl+1分別表示第l+1 層的輸入和輸出；W為權(quán)重；б(?)為激活函數(shù)，一般采用ReLu 函數(shù)。

原始輸入經(jīng)過卷積層之后，仍然攜帶較多的特征；此時再進入池化層，將特征矩陣分塊，取其最大值（即最大池化）或取其平均值（即平均池化）。該過程可以表示為：

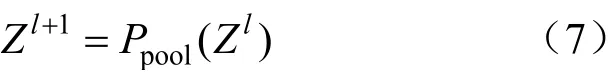
式中：Ppool(?)表示池化層的輸出。

經(jīng)過池化層降維后的數(shù)據(jù)被整合成固定長的特征向量。然后，全鏈接層對提取的特征進行非線性組合以得到輸出。該過程可表示為：

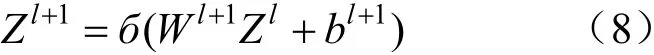
CNN 的輸出層為一個線性層，最終輸出一個向量。

1.4 損失函數(shù)

在模型訓練過程中，使用隨機梯度下降優(yōu)化算法不斷更新權(quán)重和偏置。

采用的損失函數(shù)為均方誤差函數(shù)：

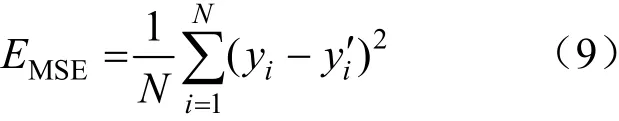
式中：N為樣本數(shù)量；分別為實際值和預測值。

1.5 預測效果評估

本文選用均方誤差和平均絕對誤差對預測的結(jié)果進行評估。平均絕對誤差的計算公式為：

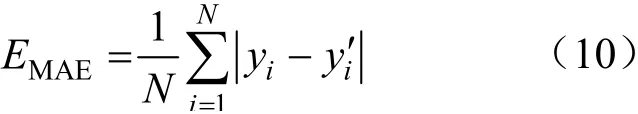
2 模型設計

如圖1 所示，本文提出的超短期風電功率預測模型主要包括數(shù)據(jù)相關(guān)性分析和功率預測2 個部分。首先將歸一化后的數(shù)據(jù)通過皮爾遜相關(guān)性分析對原始樣本中的特征進行篩選；然后構(gòu)建多頭注意力和CNN 模型；將篩選后的數(shù)據(jù)輸入模型中進行訓練，以此獲得高精度的風電功率預測模型。

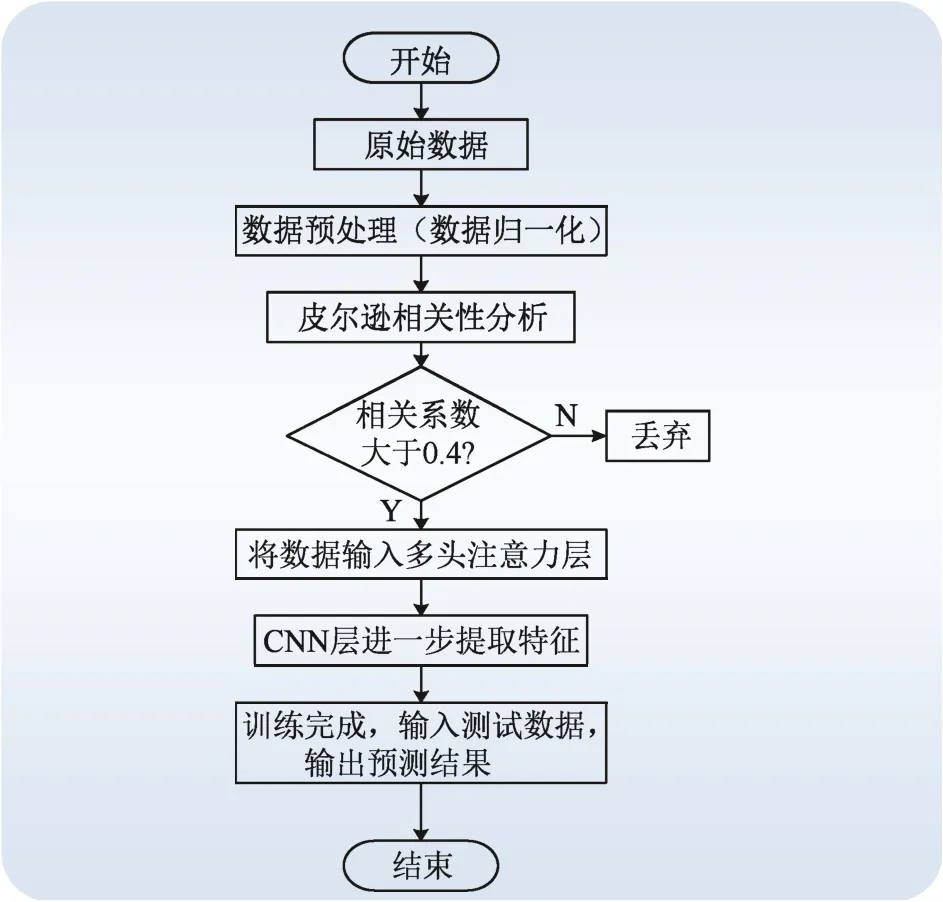
圖1 本文方法的流程圖Fig. 1 Flowchart of the proposed method

本文使用 Python 語言和 Pytorch 框架在Pycharm2021 中進行模型訓練和驗證。

CNN 各層的程序設計如下。

（1）一維卷積層1：卷積核大小設置為3；為了保持輸入的形狀，將填充設置為1，且定義10 臺濾波器。

（2）最大池化層：池化層的大小設置為3，填充設置為1。

（3）一維卷積層2：卷積核大小為3，同樣填充設置為1。

（4）全鏈接層、輸出層：通過2 個線性層得到輸出。

3 實驗驗證

3.1 數(shù)據(jù)準備和實驗設計

本文采用的數(shù)據(jù)為某風電場2015 年01 月01日—2015 年05 月14 日的實測數(shù)據(jù)。數(shù)據(jù)中，包含壓力、溫度、速度、角度等多個連續(xù)監(jiān)測項目，采樣時間間隔為10 min。

采用與文獻[20]相似的處理方法。經(jīng)標準化并1 h 平均化處理后，共得到2 923 條數(shù)據(jù)。將數(shù)據(jù)按6:2:2 的比例分為訓練集、驗證集和測試集。

為了進一步考量本文模型的預測能力，將其在測試集上的預測結(jié)果分別與單一CNN 網(wǎng)絡、單一LSTM 網(wǎng)絡和CNN-LSTM 網(wǎng)絡進行比較。

3.2 Pearson 相關(guān)性分析

共選取40個可能影響風電機組輸出功率的變量，如風速、部件溫度和轉(zhuǎn)子速度等。

為了深入了解各個變量對風電機組輸出功率的影響程度，在Pycharm 中對各個變量和風電機組輸出功率進行皮爾遜相關(guān)性分析，按公式（1）計算數(shù)據(jù)集中各個監(jiān)測項目與風電機組輸出功率之間的相關(guān)系數(shù)。計算結(jié)果如圖2 所示。

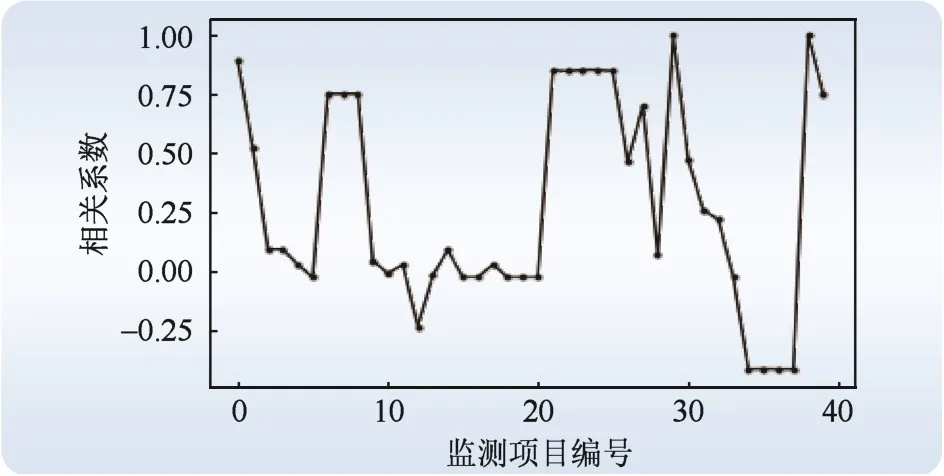
圖2 Pearson 相關(guān)性程度Fig. 2 Degree of Pearson correlation

為了兼顧預測的準確性和計算速度，只保留相關(guān)系數(shù)大于0.4 的變量。最終保留的數(shù)據(jù)變量個數(shù)為20，包括風速、轉(zhuǎn)子速度、發(fā)電機各相繞組溫度、發(fā)電機軸承溫度、機艙室外溫度、機艙溫度、塔底柜溫度、機頂盒柜溫度、主軸承轉(zhuǎn)子側(cè)溫度、換流器功率和變頻器電機速度等。

3.3 多頭注意力頭數(shù)的選擇

由于要將輸入的特征平均分配給多頭注意力的每個頭，因此多頭注意力的頭數(shù)必須能夠被輸入特征數(shù)整除。

由于篩選后特征僅剩下20 維，因此頭數(shù)只能在1、2、4、5、10 或20 中選擇。各種數(shù)量的頭數(shù)預測結(jié)果如表2 所示。

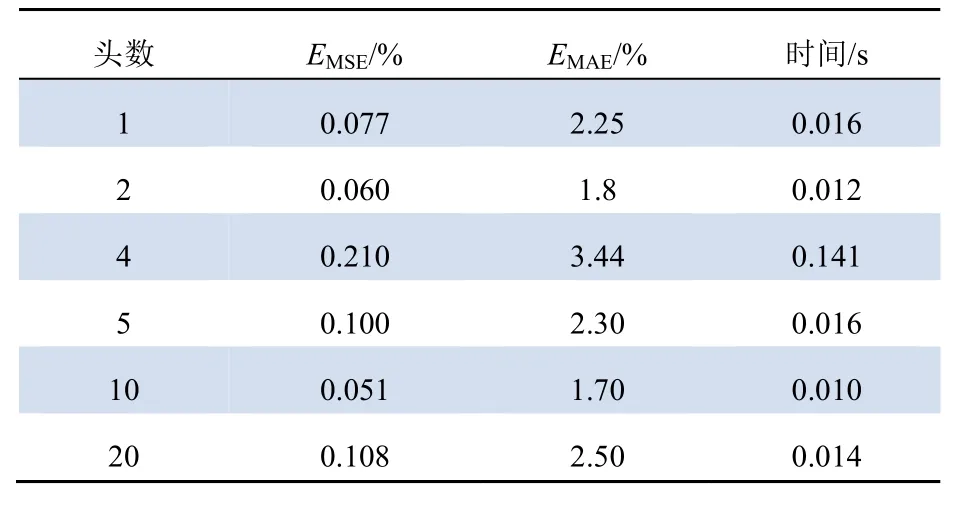
表2 不同頭數(shù)預測結(jié)果比較Tab. 2 Comparison of prediction results with different numbers of heads

當頭數(shù)增加至20 時，注意力機制將關(guān)注更多的輸入序列的特征，有可能會導致學習過多的冗余信息，從而造成模型預測效果大大降低。經(jīng)過比較，當頭數(shù)為10 時，模型的預測效果最優(yōu)。

3.4 預測結(jié)果

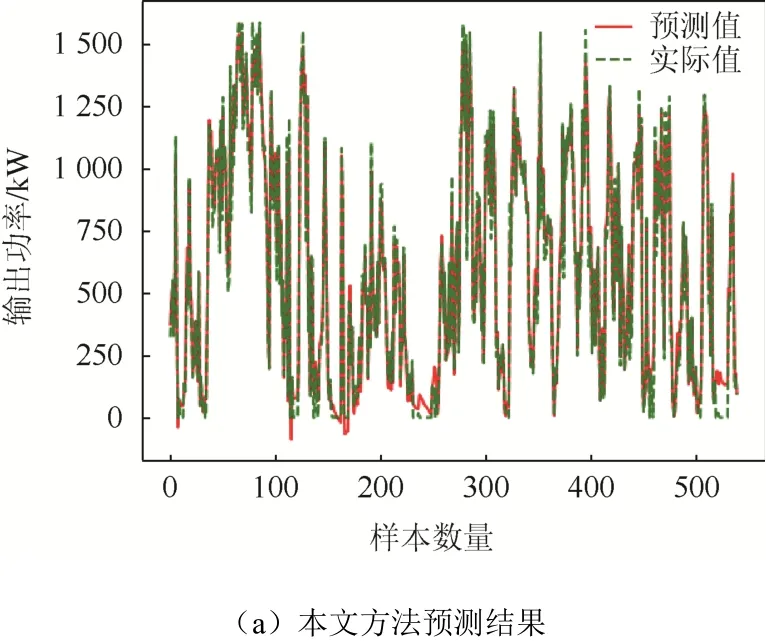
本文方法和CNN、LSTM 和CNN-LSTM 預測結(jié)果對比如圖3 所示。

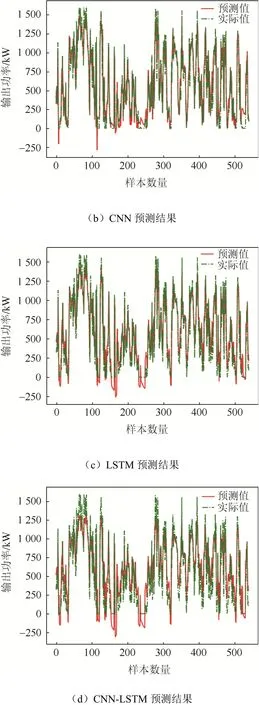
圖3 各模型的風電功率預測對比結(jié)果Fig. 3 Wind power forecasting results with the proposed method, CNN, LSTM and CNN-LSTM

3.5 各模型預測結(jié)果比較

本文方法、CNN、LSTM 和CNN-LSTM 的預測誤差對比如表3 所示。

從表3 所呈現(xiàn)的預測結(jié)果來看，本文所提模型的預測精確度和預測時間明顯優(yōu)于CNN 模型、LSTM 模型以及CNN-LSTM 模型。本文模型的EMSE值對比CNN 降低了69%，比LSTM 模型降低了90%，比CNN-LSTM 模型降低了90%；EMAE也相應降低了43%、72%、74%。

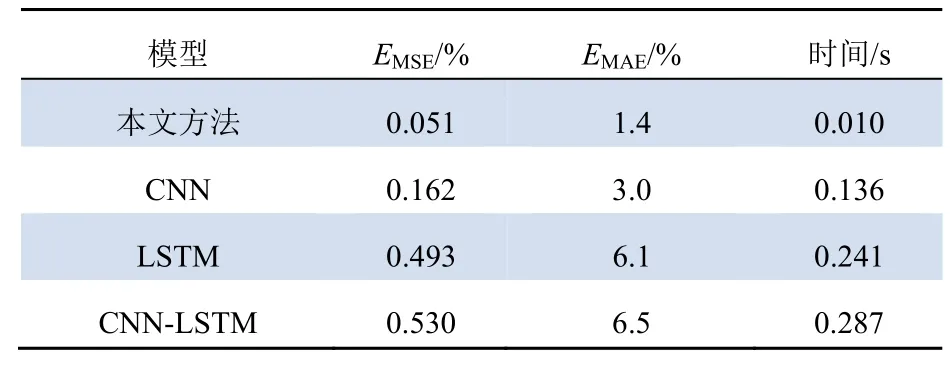
表3 各模型預測誤差和預測時間對比Tab. 3 Comparison of prediction errors and prediction time of models

綜上所述，本文模型的擬合效果遠比CNN、LSTM 和CNN-LSTM 的擬合效果理想得多，這說明：本文模型足夠充分地提取了輸入序列中的信息，預測精度達到了要求；本文提出的超短期風電功率預測模型能夠比較精確地預測風電功率。

4 結(jié)論

本文所提模型的主要優(yōu)勢在于：

（1）充分考慮了與風電功率相關(guān)的變量，對輸入序列的分析更細致，從而有效地提高了預測精度。

（2）采用注意力機制中的多頭注意力機制，彌補了CNN 池化層會丟失信息的缺點，有效地增強了模型的非線性擬合能力。

（3）與CNN、LSTM、CNN-LSTM 模型相比，該模型的預測精度更高。