基于模型預測控制的水電制氫系統優化調度研究

鄭之杰，黃靜思，黃元生

（華北電力大學 經濟管理系，河北 保定 071003）

0 引言

我國西南地區水資源儲量豐富，但利用率較低，具有進一步開發的潛能[1]。例如，大渡河、金沙江等大型水電站的水能利用率只有不到80%，小水電甚至不足60%。其原因，一是本地負荷有限，二是送出通道能力不足、網架局部阻塞嚴重[2]。

水庫承擔著供水、發電、蓄水等多種功能。提高水資源和水能資源利用率，關鍵是提高水庫的調配能力，減少棄水的發生[3]。

在碳達峰、碳中和發展目標下，我國積極推動能源改革，發展包括水電、氫能在內的綠色能源[4]。可再生能源發電制氫為解決可再生能源消納問題提供了一條實踐途徑[5]。

電解水制氫生產成本較高，在工業上難以實現規模化。利用“棄水”制氫，不僅能夠降低制氫成本、增強水電消納能力[6]，而且達到了提高水能資源利用效率的目的[7]。因此，有必要探討水電制氫系統的優化調度問題。

在可再生能源制氫系統的優化調度方面的研究中，學者們更多關注于風能、光伏與氫能系統的優化調度。文獻[8]對含氫儲能的風電系統優化調度進行了研究。文獻[9]研究了風電制氫系統的優化運行模式。文獻[10]研究了風光耦合發電中的制氫、儲氫問題，構建了日前優化調度模型。

在梯級水庫的優化調度方面的研究中，學者們對梯級水庫群的優化調度進行了大量的研究和實踐。文獻[11,12]研究了以最大化水資源利用效益為優化目標的梯級水庫單目標優化調度。文獻[13]研究了同時考慮水位控制、缺水和發電的多目標梯級水庫優化調度問題。此外，防洪風險、洪水損失率、水力發電量和滿儲率等指標在文獻[14]中被應用于評估調度策略。文獻[15]以火力發電站的發電成本和水庫棄水量最小化為優化目標，提出了梯級水庫的最優調度策略。

目前，結合棄水制氫研究水庫優化調度問題的相關文獻較少。在可再生能源制氫方面的相關研究中，關于水電制氫策略的水資源與水能資源優化調度的相關文獻也相對較少。

模型預測控制（model predictive control，MPC）是一種可用于求解耦合性強、多變量多約束優化問題的控制算法[16]。MPC 在多能系統中應用廣泛，能夠有效減少調度誤差對系統的影響，有效提高調度策略的實施效果。文獻[17]提出一種的區域綜合能源系統與電網協同的雙層多目標優化模型，并利用MPC 進行求解。文獻[18]基于MPC 建立了園區型綜合能源系統多時間尺度優化調度模型。文獻[19,20]對MPC 應用于樓宇微網開展研究，討論了可再生能源預測誤差對樓宇能量管理方案的影響。文獻[21]利用MPC 建立火電-光伏-抽水蓄能優化調度模型，以解決“大機小網”的電網結構性問題。目前，關于MPC 在水電制氫系統中應用的研究較少。

為優化梯級水庫的調度策略，提高水資源利用率和水電消納率，本文結合棄水制氫方案，建立了涵蓋經濟目標與棄水目標的水-電-氫多目標日前優化調度模型。為提高調度策略的準確性，減少日前調度模型中由于負荷不確定性造成的誤差，在日前調度模型的基礎上引入MPC 算法，建立日內滾動優化調度模型。以某河流域水庫群為算例，驗證了日前優化模型的有效性與MPC 算法對模型的改進效果，并驗證了豐水期棄水制氫方案的有效性。

1 梯級水庫日前優化調度模型

1.1 目標函數

（1）經濟效益目標

式中：Pw,i,t為t時段i水庫的對外傳輸功率；pw(t)為分時電價；Δt為時間步長；PH2,i,t為制氫功率；pH為售氫單價；ηH2為電解槽的效率；ρ是每kW·h電能產生的氫氣量。

（2）棄水目標

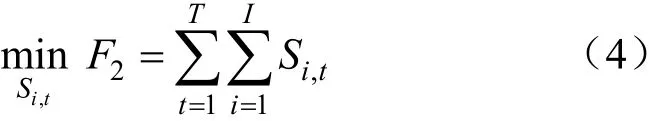
式中：Si,t為i水庫t時段的棄水量。

（3）總目標函數

本文建立的目標函數都是線性函數，目標之間的沖突與計算量較小；因此，本文選擇線性加權法進行優化求解[22]。

首先，將原目標函數進行縮放處理，如公式（5）所示：

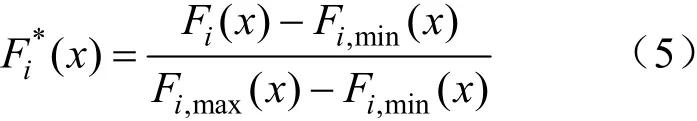
對各目標函數進行加權匯總，得到總目標函數如式（6）所示：

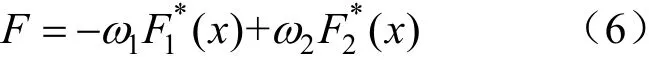
式中：ω1、ω2為目標權重；一般認為ω1+ω2=1。

1.2 約束條件

（1）混聯梯級水庫水量平衡約束

上游水庫水量平衡公式：

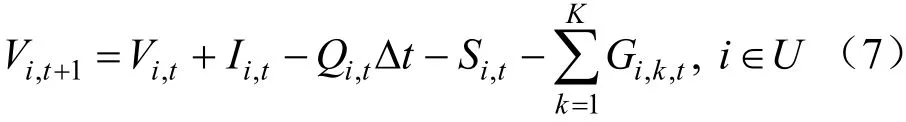
式中：U為上游水庫群；Vi,t與Vi,t+1為上游i水庫t時段的末庫容和出庫容；Ii,t為i水庫t時段的天然來水量；Qi,t為i水庫t時段的發電流量為i水庫t時段的供水量；K為水庫供水的目標城市群。

下游水庫水量平衡公式：

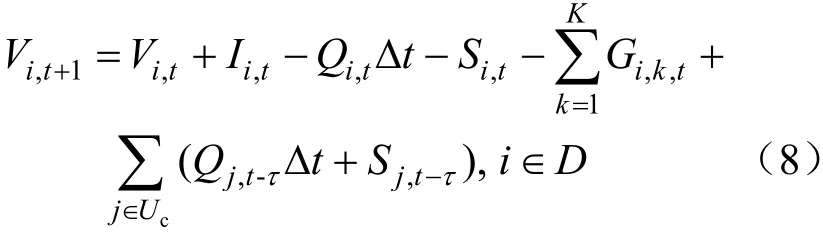
式中：D為下游水庫群；Uc為與i水庫水量相關的上游水庫群；τ為i水庫和上游j水庫之間的水流滯時。

（2）初庫容與末庫容約束

（3）供水量約束

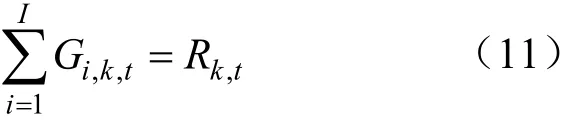
式中：Gi,k,t為i水庫t時段對k地區的供水量；Rk,t為k地區t時段的需水量。

（4）功率平衡約束

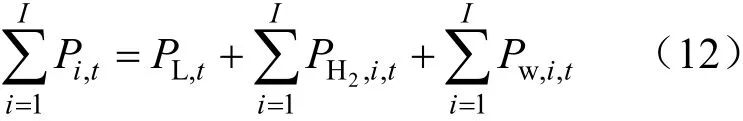
式中：Pi,t為i水庫t時段內產生的功率；PL,t為t時需滿足的常規載荷；PH2,i,t為i水庫t時段用于制氫的功率；Pw,i,t為i水庫t時的對外傳輸功率。

（5）水電站出力模型

式中：Qi,t為i水庫t時的發電流量；Hi為i水電站的水頭；ηi為i水電站的出力系數。

在水力發電公式中，發電水頭一般與上下游水位相關。上下游水位可過上下游水庫庫容推導。出力系數也是一個與水頭相關的變量。根據文獻[23,24]得：

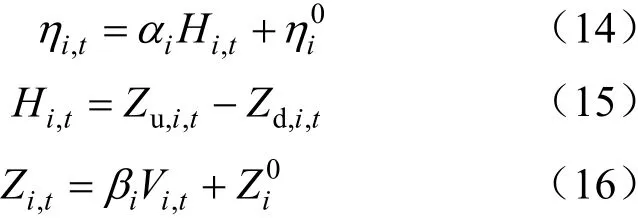
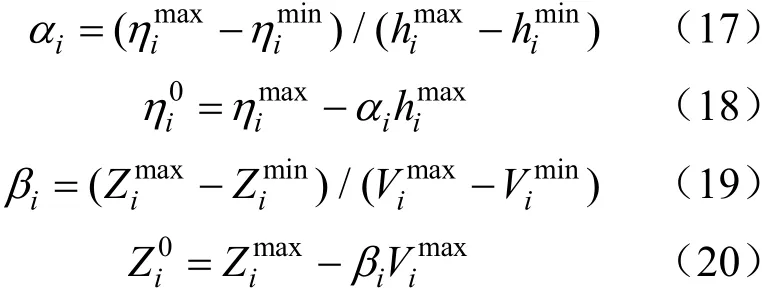
將公式（15）—（21）代入公式（14），可以得到水力發電的非線性表達式：

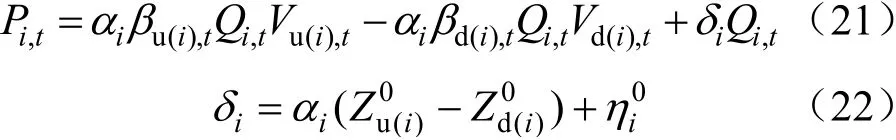
（6）非負約束

模型中所涉變量均為非負變量。

2 梯級水庫日內滾動優化調度模型

2.1 MPC 滾動優化策略

MPC 是一種滾動優化的控制算法，主要包括模型預測、滾動優化、反饋矯正3 個環節。

為解決日前調度中因負荷不確定性造成的誤差問題，本文提出一種基于MPC 的滾動優化策略，如圖1 所示。

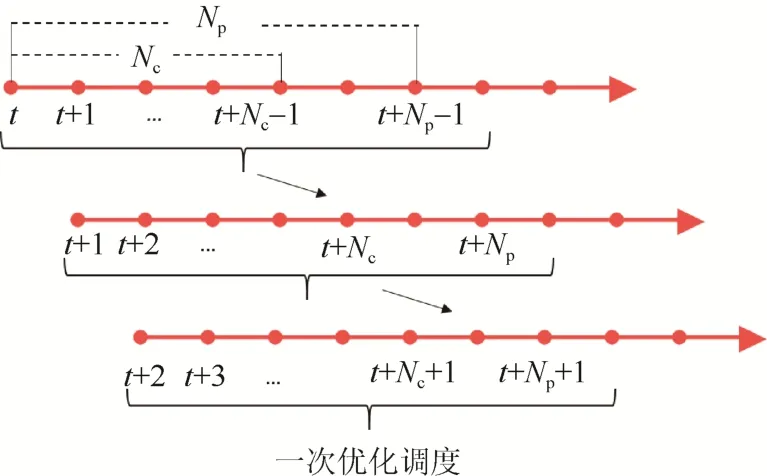
圖1 MPC 滾動優化策略示意圖Fig. 1 Diagram of MPC rolling optimization strategy

圖中，Np為預測時域，Nc為控制時域，Np≥Nc。在t時，利用預測時域內的預測數據，在控制時域內進行多目標優化調度，得到控制時域內的最優控制序列；但在當前t時段，只執行第一個控制序列的指令。令t=t+1，重復進行上一過程，直至完成整個時間軸的優化。

2.2 基于MPC 的滾動優化調度

模型計算流程見圖2。

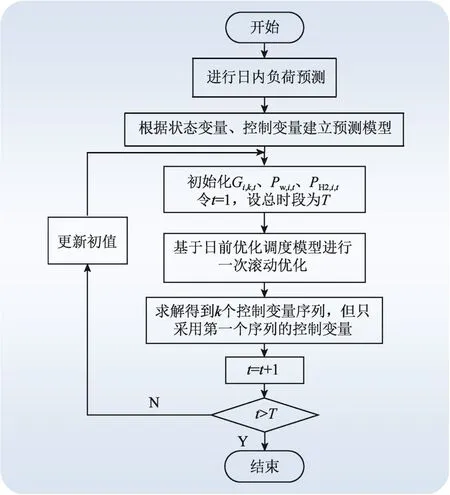
圖2 MPC 優化調度流程圖Fig. 2 Flowchart of MPC optimization scheduling

2.2.1 預測模型

在滾動優化調度中，將負荷的預測值作為模型的輸入變量。

本文采用疊加隨機預測誤差來模擬負荷預測值[20]，具體表達如下：

式中：PL,t為負荷的日前預測值；為負荷日內的短期預測值；表示輸入變量日前預測值在t時段的預測不確定閾值；R(t)為一個服從均勻分布U(-1,1)的隨機數。

預測模型的狀態變量為各水庫調度中的供水量、制氫功率與對外傳輸功率。

控制變量為供水量、制氫功率與對外傳輸功率的增量值。優化后，可得到一個控制周期內幾個控制變量的取值。利用第一個控制變量序列可得到新的預測值，預測模型建立如下。

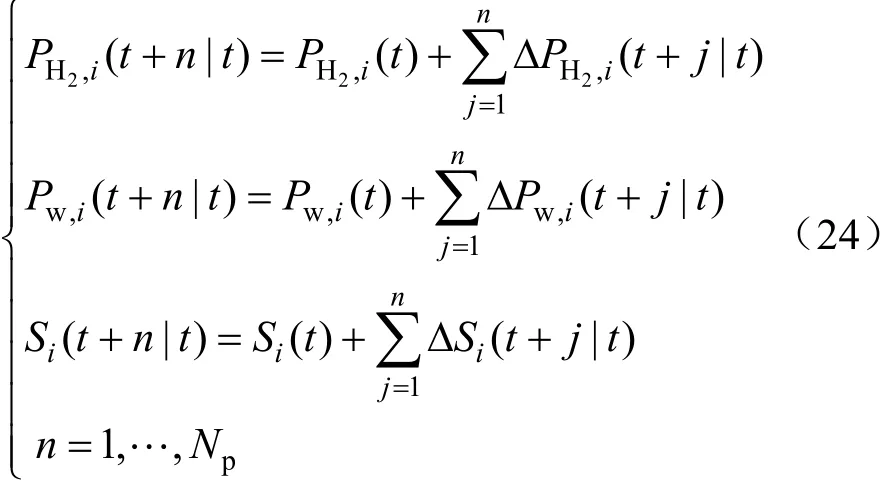
2.2.2 滾動優化

在日前優化調度模型的基礎上建立滾動優化模型。目標函數改進為如下形式：

（1）經濟效益目標

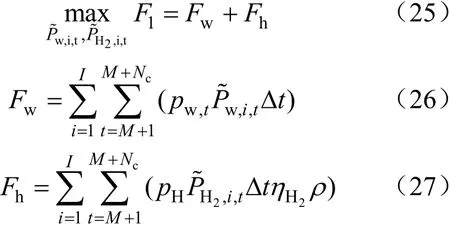
式中：pw,t為分時電價；分別為當前時刻對未來對外傳輸功率與制氫功率的最優決策值。

（2）棄水目標

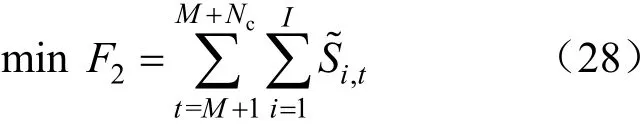
為適應模型在Nc時域的滾動優化，將約束時域從整體時域改為局部控制時域即Nc，具體形式如下：

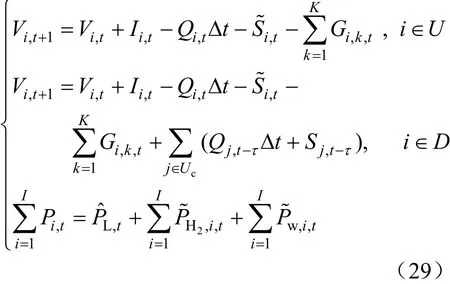
其余相同約束不再贅述。

2.2.3 反饋矯正

在第t時刻進行一次優化調度，可得到k個決策變量序列。只采用第一個序列的決策變量值，并在t+1 時刻利用實測值來更新預測模型中的初始值，即從而進行新一輪的滾動優化。

3 算例分析

3.1 基本數據

本文以洪汝河流域的梯級水庫群數據為例來驗證模型的有效性；利用MATLAB 軟件通過Yamlip語言建模并調用fmincon 求解器求解非線性模型。

洪汝河流域涵蓋石漫灘水庫、板橋水庫、薄山水庫和宿鴨湖水庫4 個水庫。這4 個水庫需要對流域周邊的10 個城市進行供水。每個水庫都配有一個制氫站，用于進行水電制氫。4 個水庫的基本參數如表1 所示。

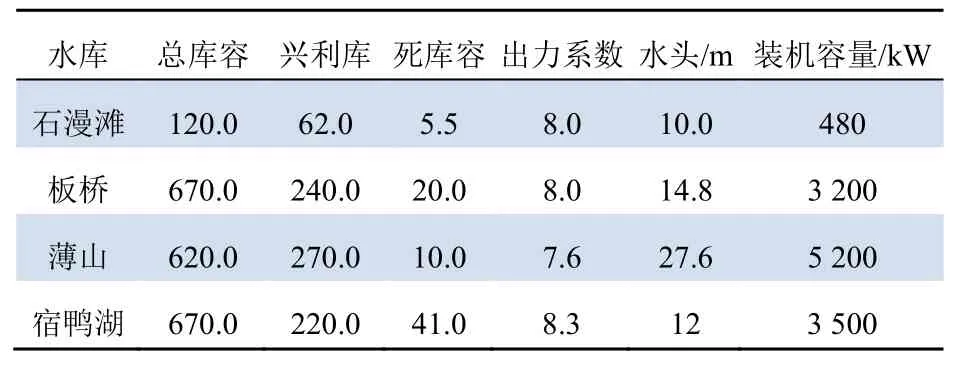
表1 水庫參數Tab. 1 Reservoir parameters×105 m3

如圖3 所示，4 個梯級水庫為混聯結構，其中石漫灘水庫與其他3 個水庫并聯，板橋水庫與薄山水庫并聯，宿鴨湖水庫與板橋、薄山水庫串聯。

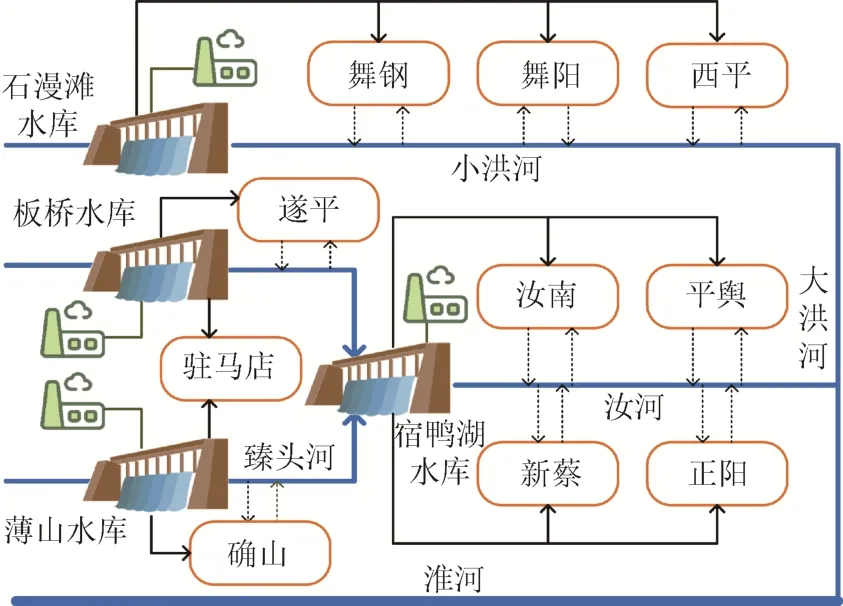
圖3 洪汝河流域示意圖Fig. 3 Schematic diagram of Hongru River Basin

各水庫在提供供水服務的同時承擔發電任務，其日負荷需求曲線如圖4 所示。

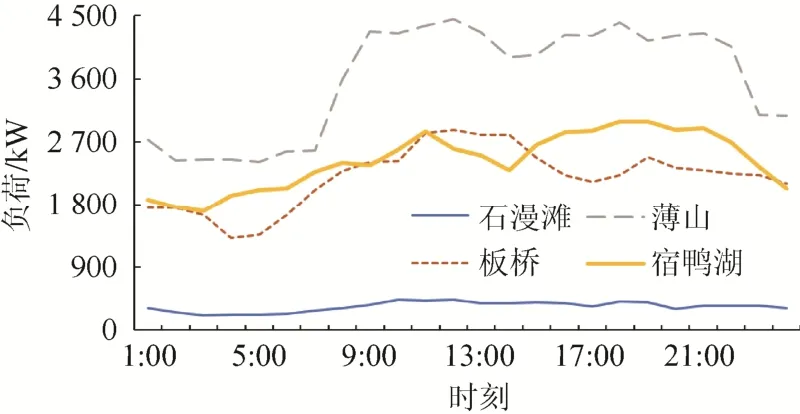
圖4 各水庫日負荷曲線Fig. 4 Daily load curve of each reservoir

為更好地模擬模型優化情況，本文采用分時電價策略。發電側與售電側分時電價峰谷時段劃分一致[25]。分時電價設定參考該省電網峰谷分時電價的數據。設定電價：高峰，0.89 元/kW·h；平段，0.58 元/kW·h；低谷，0.31 元/kW·h。同時，氫價設定[26]為3.3 元/m3。

3.2 優化目標權重分析

從提高經濟效益和減少棄水2 個方面進行優化。

為驗證單目標優化是否能達到最優，根據單目標分別進行優化求解，結果見表2。

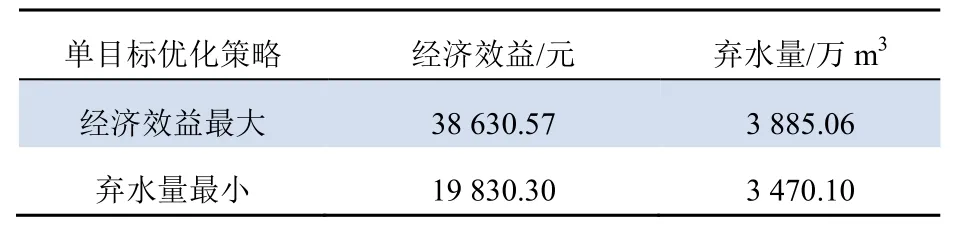
表2 單目標優化結果Tab. 2 Single objective optimization results

從表2 可以看出：當以經濟效益最大化為目標進行優化時，優化后可以獲得更高經濟效益；但是，該結果對棄水量的優化并不明顯。以最小棄水量為優化目標時，雖然較大程度地減少了棄水，但不能兼顧經濟效益的提高。因此，需要進行多目標優化調度。

經濟效益與棄水量存在相關影響，因而目標權重的差異會致使不同的優化結果。基于目標函數中ω1+ω2=1，本文提出9 種權重組合的調度方案，優化結果如表3 所示。

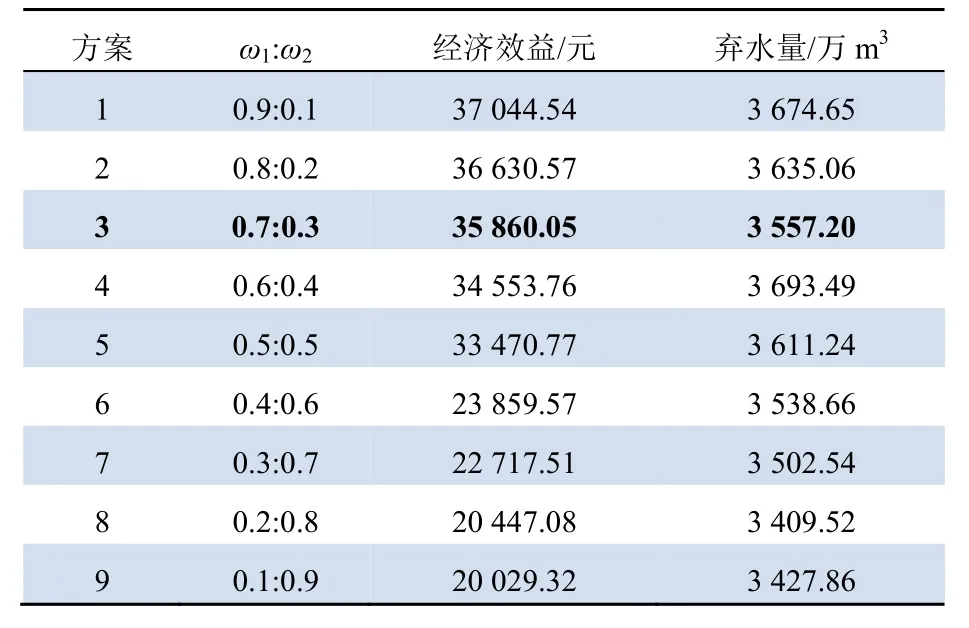
表3 不同權重組合調度方案的優化結果Tab. 3 Optimization results of different weight combination scheduling schemes

表3中，方案3：ω1=0.7，ω2=0.3。該方案在提高經濟效益的同時，較好地兼顧了各水庫間的水能利用效率。因此在接下來的案例分析中，將把權重設定為ω1=0.7，ω2=0.3 來進行分析。

3.3 日前優化調度結果分析

若按照常規運行，水庫不包括棄水制氫。假設可消納水電全部售出，則可獲得的單日經濟效益約為24 116 元。

加入包含棄水制氫的優化調度后，可得到用于制氫和對外傳輸的功率，如圖5 所示。此時的經濟收益包括售電與售氫2 部分，單日經濟效益為35 860 元，較優化前增加了11 744 元。

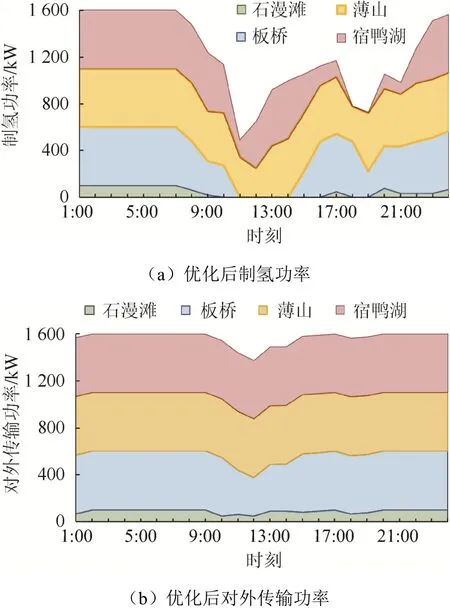
圖5 優化后的水電調度計劃Fig. 5 Optimized hydropower dispatching plan

由圖5（a）和圖5（b）可以看出，為獲得最大收益，水庫在早晨的1:00 至8:00 優先進行電解水制氫消納多余水電。在該時間段，售氫單價要大于分時電價。由于余下時間段電價較高，多余的水電將優先出售給電網。

根據數據估計，優化前豐水期的單日棄水量約為3 755.5 萬m3。在將氫氣生產整合到水庫調度系統的情況下，水電的消納能力有效提高，梯級水庫的棄水量明顯減少。優化后，棄水量為3 637.2 萬m3。其中，薄山水庫與石漫灘水庫可達到零棄水，宿鴨湖水庫與板橋水庫較優化前可減少198.5 萬m3的棄水量，棄水情況如圖6 所示。

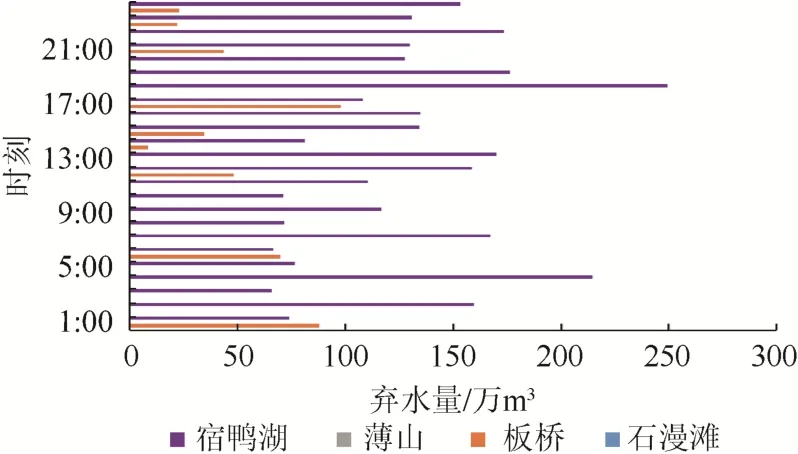
圖6 各水庫棄水量Fig. 6 Amount of abandoned water by each reservoir

優化前后各目標對比結果如表4 所示。

表4 優化前后對比結果Tab. 4 Comparison results before and after optimization

3.4 日內滾動優化調度結果分析

負荷的不確定性，使得模型優化的實施效果與計劃存在偏差，主要體現于系統的經濟效益目標。

假設日前調度的負荷曲線與實際負荷曲線存在10%誤差。若將日前調度計劃按照實際負荷進行實施，下發的發電計劃則與實際用戶負荷不匹配，這會使得用電調度無法完全按照最優方案進行，因此會導致收益減小。

為應對負荷不確定性，減少經濟損失，本文進行了基于MPC 的日內滾動優化。

優化后，得到新的制氫與對外傳輸功率調度方案。基于MPC 的優化調度模型在經過滾動預測后，其負荷曲線精度更高，與實際負荷曲線的誤差可減小至3%。

MPC 調度策略調度結果如圖7 所示。基于MPC的優化調度模型得出的發電計劃更貼近實際用電情況。

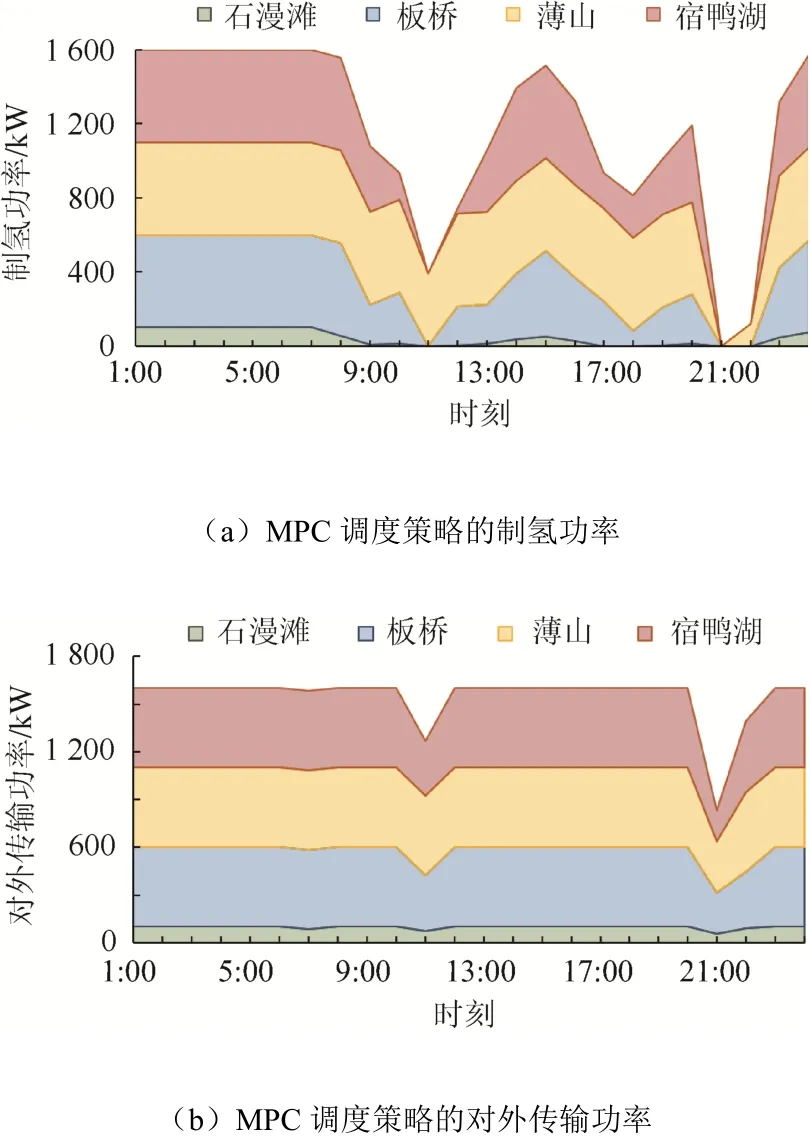
圖7 MPC 策略水電調度計劃Fig. 7 MPC strategic hydropower dispatching plan

將日前調度策略與基于MPC 的調度策略的總體實施情況進行對比，結果如表5 所示。

通過表5 結果對比可以得出：按照日前策略可得的實際總經濟效益為32 827.82 元；按照MPC策略實施所得的實際總經濟效益為33 841.8 元，較日前調度方案的經濟效益增加了1 013.98 元。

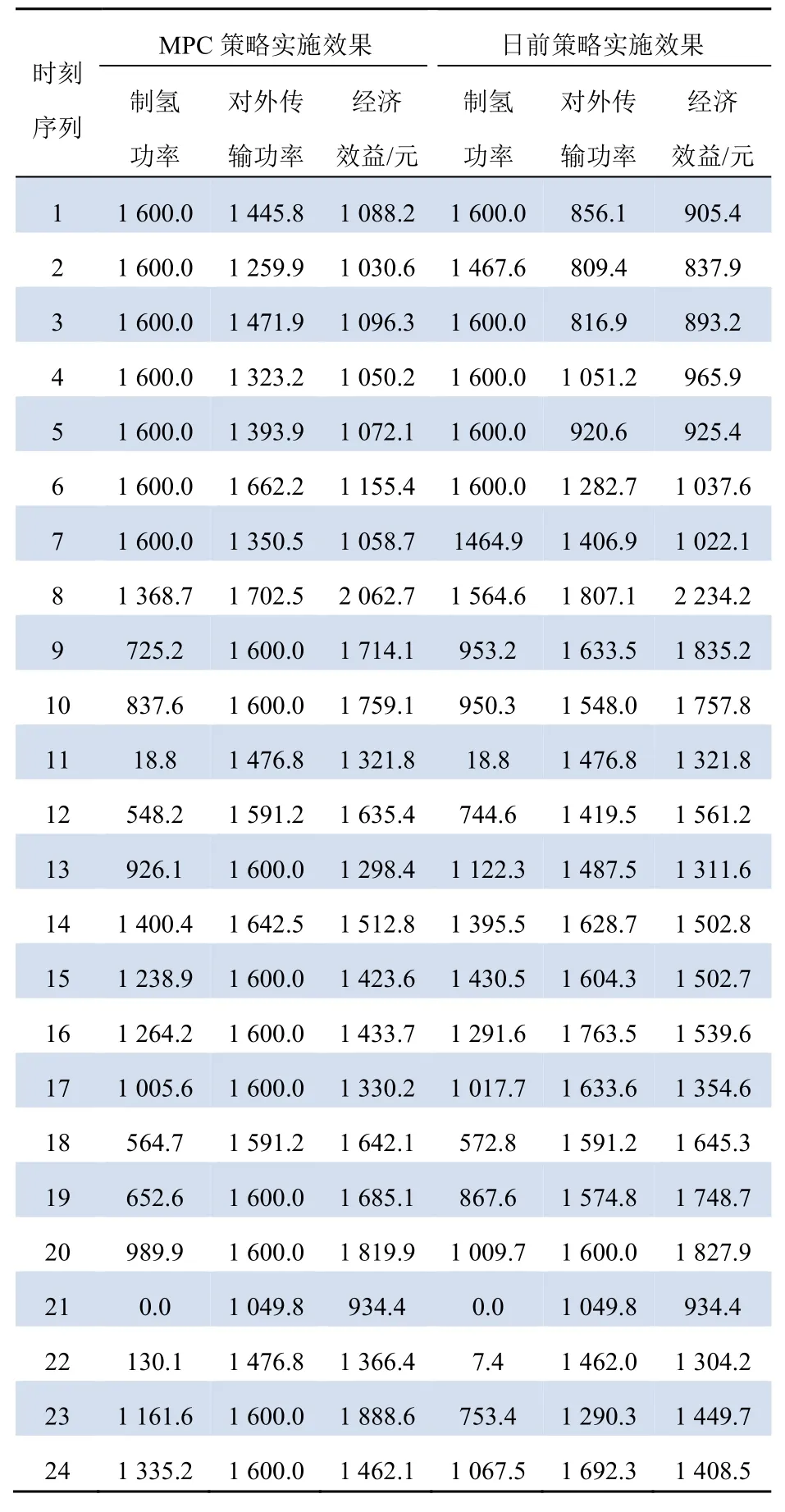
表5 MPC 策略與日前策略實施效果對比Tab. 5 Comparison of the effect of MPC strategy and day-a-day strategy kW

4 結論

本文在已有水庫發電系統運行方案的基礎上，接入電解水制氫系統，開展了水-電-氫多能系統的日前優化調度研究。考慮到負荷不確定性，引入MPC 對多目標優化模型進行日內滾動優化。算例驗證結果表明：

（1）水-電-氫多能聯合優化調度系統可顯著提高流域的經濟效益。與優化前相比，系統單日經濟效益增加11 744 元。在用電低峰期開展棄水制氫，能有效提高經濟效益。

（2）接入水電制氫后，水電消納能力得到有效提高，發電流量增加，棄水量減少。優化后的單日棄水量可減少198.5 萬m3。

（3）MPC 算法的應用有效降低了因負荷不確定性造成的經濟效益損失。經滾動優化后，負荷預測精度有所提升，使制氫與對外傳輸功率計劃更貼近實際情況，所得實際效益比日前調度策略增加了1 013.98 元。