大直徑鉆孔灌注樁優化設計研究

孔凱歌，伍曉偉，王 曉，石忠利

(廣西交通設計集團有限公司，廣西 南寧 530029)

0 引言

開展樁基設計時，在滿足基本力學性能及變形性能的基礎上，往往存在一個最佳經濟效益的尺寸。但目前我國的設計仍以承載力、耐久性等作為主要因素[1]，而在考慮經濟性時依賴于經驗來確定最佳方案。

樁基的優化設計涉及結構、巖土等多個領域，并借助數學及邏輯推理等方法來使得設計方案能夠在可行范圍內得到最大程度的優化。實踐表明[2-3]，借助樁基的優化設計能夠顯著改善其設計的科學性與可行性，并將設計周期控制在合理范圍內，使得方案的綜合效益得到有效提升。本文基于我國現行行業規范對灌注樁設計暴露出的問題進行分析，并以此為基礎深度優化設計方案，同時利用Matlab軟件分析來得到優化方程組的解，從而確定樁基設計優化后的尺寸。

1 大直徑鉆孔灌注樁單樁非線性最優解

目前，我國灌注樁的設計主要采用經驗法進行計算，并與靜載試驗相結合，以樁的計算長度作為計算參數，以此來優化樁的設計。其單樁豎向極限承載力計算如式(1)所示：

(1)

由此可以得到大直徑單樁豎向極限承載力的設計值如式(2)所示：

(2)

式中，γs、γp分別為樁側阻和端阻抗力分項系數。

根據式(1)、式(2)即可發現單樁承載力的主要影響因素有樁基尺寸u、l、Ap及樁周土體承載力qski、qpk。

1.1 模型的目標函數

在其他各項參數滿足要求的基礎上，當單樁承載力達到設計承載力R時對應的體積V最小，此時施工所需的材料也最省，達到最為經濟的狀態，其計算如式(3)所示：

(3)

1.2 承載力約束下的單樁優化設計準則

基于最優化非線性準則而展開的單樁優化設計，不僅計算過程比較繁雜，而且適用范圍也比較有限，無法很好地滿足具體需求，難以在實際工程中得到廣泛應用[4]。在這樣的背景下，本文提出了遺傳算法下的大直徑鉆孔灌注樁優化設計。

2 基于遺傳算法的樁基優化

上文所論述的設計過程是我國橋梁工程傳統設計中比較常用的一種方法。值得注意的是，該方法在優化時僅僅考慮了預期承載力的目標要求，而對其他約束條件未能加以考慮，且只能用于均質土體中樁基的設計[5]。但遺傳算法的引入能很好地解決這一問題，可以滿足多約束條件的限制，對目標函數進行求解，方程組如式(4)所示：

(4)

作為數學求解中常用的高級語言，Matlab軟件語言在工程分析中發揮著至關重要的作用，其不僅具有豐富的功能，同時運算邏輯比較簡單，適用性較強。內嵌于Matlab軟件中的遺傳算法工具箱能夠綜合調用多重函數，以此來適應不同優化條件及需求下的計算工作[6]。

在借助Matlab軟件進行遺傳計算之前，首先需要編制M文件，在該文件接收行向量的同時能夠相應地返回標量，所接收的行向量應當與適應度函數相對應。

在開展大直徑鉆孔灌注樁優化工作時，適應度函數可按照式(3)確定，同時也可改寫為式(5)：

(5)

在編制M文件時應當將其設定為能夠接受長度為2的行向量X，且其分別與變量l和d相對應，向量所返回的標量與函數值保持相等。

在以遺傳算法對大直徑鉆孔灌注樁展開優化設計時，可以轉化為在相應約束條件下的數學模型，并對其進行多元多峰適應度函數的優化求解[7]。這一計算過程可借助Matlab軟件完成。

優化設計開始前，首先需要將適應度函數M存儲在相應的文件目錄中，且其至少需要囊括約束條件M文件、適應度函數M文件和遺傳算法源程序M文件三類文件[8]。為便于計算，本文將有約束的優化計算轉變為無約束條件下的適應度函數尋優求解，所以在M文件中僅有適應度函數M文件。適應度函數M重命名為fitness.m，設計優化所需的源程序可由Matlab軟件自動運算得到，M文件編制完成后即可求解目標函數的最優解。

3 靜載荷試驗研究

3.1 工程概況

本文以我國某橋梁工程為例展開分析。該項目設計全長約為6 851.4 m，橋面設計寬度為42 m。在橋梁設計范圍內共有1 614根鉆孔灌注樁，為便于標準化施工，將其樁徑設為1.2 m、1.3 m、1.8 m三類，符合大直徑鉆孔灌注樁的要求。本研究設置有Z1、Z2兩根試樁，兩根樁的長度分別為36.0 m、25.0 m，樁體材料選用C20級混凝土。按照灌注樁樁側及樁端的土體即可初步判定樁的承載力主要由樁側阻力構成，可視為摩擦型樁。樁孔開挖選用旋挖鉆成孔的施工方式，且借助膨潤土來形成泥漿護壁以建立穩定的施工環境。泥漿各項設計指標滿足相關規范標準要求，且在鉆孔施工中開展二次清孔。

3.2 試驗結果分析

借助試樁試驗實測數據，可初步分析得到樁基的承載能力，并以此為基礎明確極限狀態下樁側及樁端阻力的工作狀態，為樁基設計優化提供基礎數據指導，盡可能提升項目整體的經濟效益[9]。

試驗過程采取逐級加載的原則，對于逐級荷載的加載量可按最大加載量的1/10進行確定。在每一級加載結束后的第5 min、10 min分別讀數一次，隨后可按15 min的間隔時間進行讀數，在加載結束1 h后按照30 min的間隔時間進行讀數。在加載過程中，應將每小時沉降量控制在0.1 mm以內，連續三次觀測值得到每小時沉降量滿足要求時，即可認為已經達到穩定狀態，可開始下一級荷載的施加。當加載環節結束之后，即可開始逐級卸載直至荷載為零。其中，每一級的卸載量以加載量的2倍為宜，在每級卸載完成后的第15 min、30 min、60 min各讀取一次殘余沉降量，隨后開始下一級卸載。當卸載全部結束后的第3 h還應再讀數一次。如有必要，可在樁體內埋置滑動測微計來實時獲取樁的內力水平，同時還應在樁頂之下約40 cm的位置處以正交的方式布置兩個百分表來獲得樁基實際沉降量。

3.2.1 荷載-沉降曲線

根據兩根試樁的荷載、沉降變化數據即可得到如圖1、圖2所示的荷載-沉降曲線。

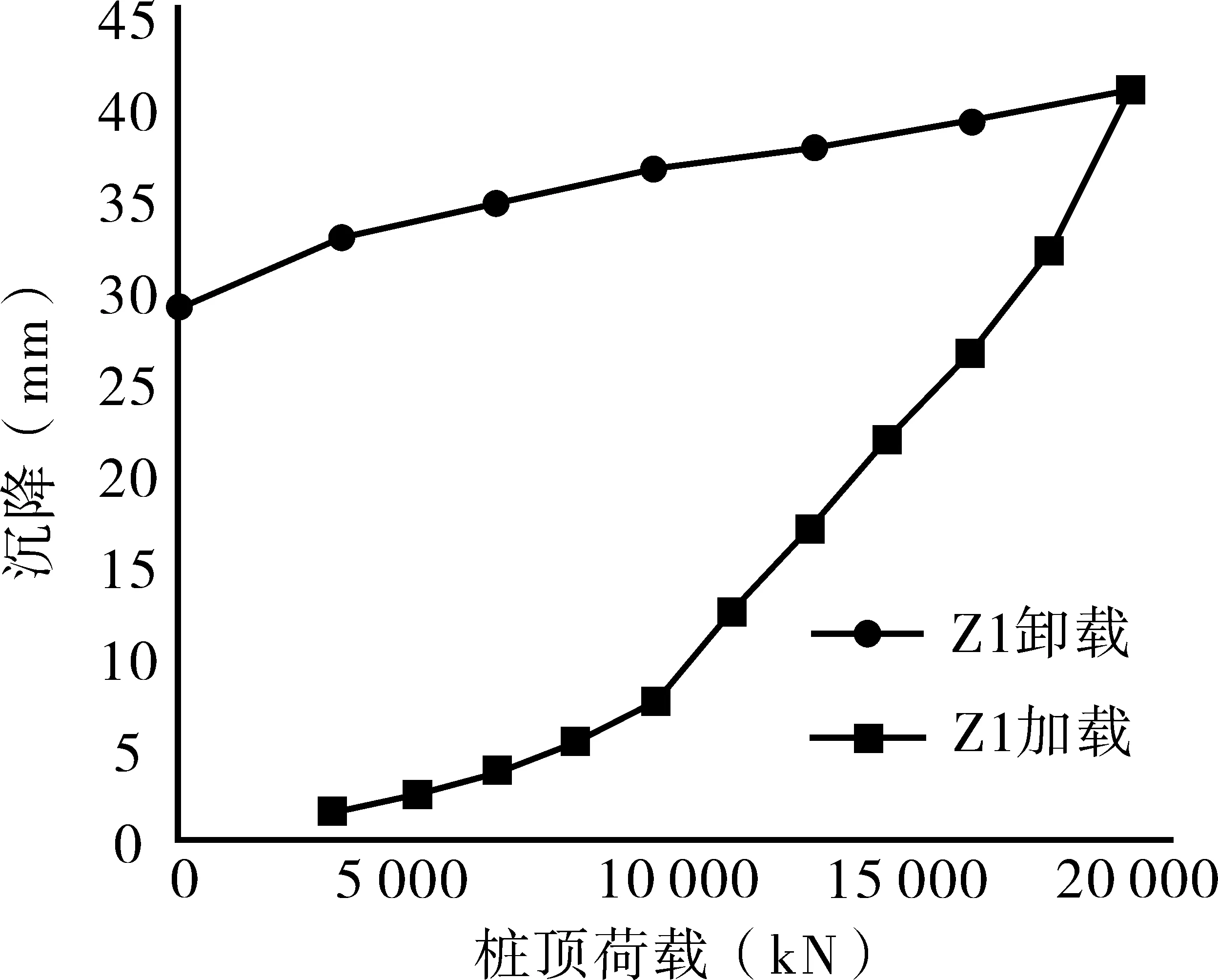
圖1 Z1樁的荷載-沉降曲線圖

圖2 Z 2樁的荷載-沉降曲線圖

試驗測得Z1試樁的最大加載量、最大沉降量及最大回彈量分別為24 000 kN、40.525 mm及11.387 mm，計算得到其回彈率約為28.1%；Z2試樁的最大加載量、最大沉降量及最大回彈量分別為28 000 kN、40.969 mm及6.689 mm，計算得到其回彈率約為16.3%。

圖1、圖2分別展示了試樁實測的極限承載力，且根據圖中曲線能夠初步判斷得出不同樁長下單樁極限承載力的變化趨勢。樁長的增加對于單樁極限承載力而言有著積極作用。當兩組試件的樁長從25 m提升至36 m時，樁長增加幅度為44%，而其單樁極限承載力的增幅分別為33%及22%。由于摩擦型樁的承載力主要由樁側阻力構成，同時樁側阻力與樁土相對位移大致存在正相關關系，若樁長保持增長趨勢，荷載在樁體中傳遞時會逐漸向著樁周土中擴散，在樁底位置的荷載水平一般較小，且樁土位移也將處于較低水平。

3.2.2 樁身軸力及樁端阻力的發揮

由Z1、Z2試樁的樁身軸力分布情況可知，樁內軸力在樁體不同位置處的分布可以基本體現出荷載作用下樁側及樁端阻力的發揮程度。根據本試驗中所用的兩種不同尺寸試樁可以發現，軸力沿樁身的分布基本相同，即在樁體越深的位置軸力越小，且呈現出線形變化的趨勢。若在樁頂施加的荷載水平較低，則在內力傳遞過程中樁端位置的軸力水平可近似看作為零。在這樣的情況下，樁身及樁周土都是彈性狀態，所以軸力呈現出線形減少的分布狀態。而隨著施加在樁頂的荷載不斷增加，樁體內軸力的減小速度也隨之提升，樁周土逐漸表現出更加顯著的塑性性質，樁端土對內力的分擔作用也越來越顯著。

3.2.3 樁側摩阻力的發揮

由Z1、Z2試樁的樁側阻力分布情況可知，在不同水平的樁頂荷載作用下，沿樁體分布的樁側摩阻力大致呈現出拋物線的形狀，且在樁身上的一定區段內，樁側摩阻力可被看作線形遞增。所以，樁側摩阻力整體的分布可描述為“單峰狀”，其承載能力的最大值位于樁身的0.5～0.7L處。在計算時，可以將該點簡化至樁頂下2/3L位置，其中L為樁的計算長度。由此可以發現，樁側摩阻力的大小及分布與土體性質有著顯著關聯性。在樁體的上側，由于受到樁頂荷載作用，樁體會發生一定程度的彈性變形導致樁土間的相對位移持續增大，甚至可能達到極限位移量，在這一狀態下樁側摩阻力也將達到極限，其值與土體對樁體的側壓力呈現出正相關關系。而在樁體的下側，由于樁體內軸力不斷向下傳遞至土體中，樁土間的相對位移會產生一定程度的減小，在低于極限位移時，樁土相對位移越小則樁側阻力越小，且與樁的入土深度有著正向關系。

4 樁基優化設計

4.1 設計參數

在M文件編制完成后，即可對Z1、Z2試樁的幾何尺寸展開優化，并基于試驗實測數據得到相應的參數，如表1所示。

表1 優化設計中的已知參數表

在優化試樁的幾何尺寸時，需要忽略樁長、樁徑以及長徑比的限制作用，并且確保優化后的單樁體積小于原試樁體積，那么就需要附加約束函數式(6)：

(6)

式中：d、d0——分別為優化樁和原試樁的樁徑，對于Z1、Z2均取d0=1.3 m；

l、l0——分別為優化樁和原試樁的樁長，Z1中l0=36 m，Z2中l0=25 m。

將上述參數引入適應度函數中進行計算。

4.2 計算結果分析

借助Matlab軟件的遺傳工具箱對原試樁進行優化設計，計算結果如圖3～4所示。

(a)適應度值

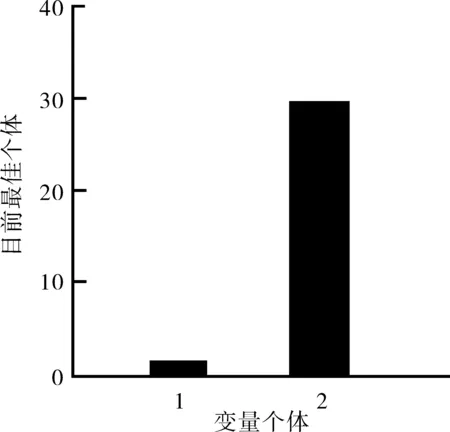
(b)目前最佳個體

(a)適應度值

(b)目前最佳個體

表2 遺傳算法優化計算結果對比表

由于鉆孔灌注樁在施工時涉及成孔、扎筋、澆筑等多個環節，在通過遺傳算法對設計方案進行優化時給出了相應的樁長及樁徑建議值。對比優化方案與原方案發現，在得到最優解時所對應的樁長較原方案更短，樁徑較原方案更大(見表2)。同時，經計算發現，試樁優化后的體積較原方案分別減少約3.35%及5.13%。由此可以認為，借助遺傳算法優化設計方案，能夠在保證承載能力、沉降量均符合要求的同時，有效減少材料的用量，進而取得更高的經濟效益。同時，根據表2中的方案對比可以發現，原設計中的試樁體尺寸符合要求。

基于表2中的數據，假定在優化設計時保持原有方案的配筋不變，不考慮方案變更帶來的鋼筋用量減少，可得到優化方案的成本節約量，如表3所示。

表3 單樁混凝土節約量計算結果表

樁基工程涉及內容比較復雜且工序繁多，在具體的工程中優化設計方案不僅能夠達到節約資源、降低成本的目的，同時還對施工的其他方面產生著影響，譬如降低人工作業需求、縮減工期等[10]。由此可見，該樁基設計方案的優化具有突出的綜合效益優勢。

5 結語

(1)借助試驗確定樁基的荷載-沉降曲線以及樁身軸力和樁側阻力分布曲線，對其進行分析即可總結得到樁頂荷載作用下樁體內力傳遞規律，發現荷載-沉降曲線整體較為平緩。而隨著樁長的不斷增加，樁體承載力表現出逐漸上升的趨勢，且其增幅逐漸減小。

(2)基于最優化準則建立鉆孔灌注樁的優化分析模型，同時按照非線性規劃法能夠得到目標函數Vmin，借助Matlab軟件對其進行分析即可獲得優化方程組。

(3)實踐表明，遺傳算法不受土體性質、截面形式等的影響，在不同工程中均具有較好的適應性。

(4)在完成目標函數及M文件的編制后，借助Matlab軟件模型進行優化分析，得到Z1、Z2的優化后尺寸，并結合工程實際條件給出相應的建議值。分析數據表明，優化后的單樁體積較原方案分別減少了3.35%及5.13%，表明Matlab軟件的優化具有充分的合理性及可行性。