后向臺階繞流低頻脈動特性的強化傳熱研究

謝緯安，喜冠南，李驕承

（1.南通職業大學汽車與交通工程學院，江蘇 南通 226007；2.南通大學機械工程學院，江蘇 南通 226019）

1 引言

后向臺階結構引發的后向臺階繞流具有豐富的流動現象，在工程中也有廣泛的應用，例如流體流過建筑、換熱器、燃燒室以及電子設備的冷卻系統中均有涉及。國內外學者對該流動現象開展了大量的研究，其中文獻[1]的實驗研究具有代表性，對推動臺階繞流研究的發展起到了一定作用。他們通過激光多普勒實驗得到了不同流動狀態下后向臺階繞流的分離與再附位置，并根據再附位置的變化特征對流動狀態進行了區分。

在層流區域，文獻[2]數值模擬了進口擾動條件下后向臺階繞流的流動傳熱，結果表明共振頻率的進口來流增強了臺階下游4倍臺階高范圍內的傳熱，非共振頻率的進口擾動未能強化傳熱。文獻[3]的實驗研究同樣得出，脈動進口來流能夠部分恢復穩定層流流動在臺階下游損失的傳熱性能。關于脈動進口來流的作用，文獻[4]還指出在層流混合對流時，雷諾數、理查德森數和振動頻率對流動和傳熱都有明顯影響。文獻[5]研究了頂面布置振動翅片對后向臺階繞流傳熱特性的影響，具體分析了振幅和頻率的作用。文獻[6]研究了三維后向臺階繞流的努塞爾數的峰值分布特征。文獻[7]模擬了內插固定圓柱對后向臺階繞流傳熱的影響，結果表明內插固定圓柱可以使底面努塞爾數峰值最大提高155%，但底面平均努塞爾數略有下降。文獻[8]模擬了進口脈動來流、內插固定圓柱條件下的后向臺階繞流的流動傳熱，結果表明傳熱性能隨脈動頻率的增大而增強。此外，文獻[9]利用微流量傳感器和高速攝像機對低雷諾數下的后向臺階繞流進行了流動實驗，發現底面和頂面附近的流動都存在一定的周期特征。

過渡流區域，文獻[10]模擬了過渡流下后向臺階進口掃流的分離再附流動，主回流區的尺度隨著掃流入射角度的增大而減小，尤其是入射角度大于40°后，再附著長度顯著減小。文獻[11]的研究也表明在掃流入射角度達到40°時，再附著長度顯著減小。文獻[12]對后向臺階繞流中旋渦的主動控制進行了模擬，分析了進口脈動來流和臺階垂直面上振動射流的作用。

在湍流區域，文獻[13]通過PIV實驗研究了層流到湍流下后向臺階繞流的流動特性，分析了后向臺階繞流中的旋渦結構和后向臺階繞流起動流的發展與演變。

發現隨著雷諾數的增大，剪切層中大尺度旋渦的數量逐漸減少，并將后向臺階繞流起動流的發展過程分為4個階段。文獻[14]采用等離子發生器控制湍流下的后向臺階繞流的流動，發現在臺階分離點上游設置等離子發生器比在主回流區內設置能更有效地減小主回流區大小。

文獻[15]的實驗研究結果也得出在臺階分離點上游設置等離子發生器對減小再附著長度最為有效。文獻[16]通過PIV實驗研究了臺階邊緣上的周期射流擾動對湍流下后向臺階繞流的影響，得出該擾動最多能夠將回流區長度減小20%。

文獻[17]實驗研究了不同頻率擾動下后向臺階流的湍流流動特性，得出外加擾動的斯特勞哈爾數為0.19時，對減小再附著長度最有效。

通過對以上后向臺階繞流研究現狀的分析可以發現，關于流體振動特性對流動傳熱影響的研究多集中在層流和湍流區域。且這些研究均是采用主動控制的方式來實現流體的振動。而關于過渡流下后向臺階繞流自激震蕩對流動傳熱影響的研究很少。因此，本文針對過渡流下后向臺階繞流自激振蕩引起的低頻脈動特性，重點分析該流動特性對臺階底面傳熱的作用。

2 研究方法

2.1 物理模型及邊界條件

在本文所研究的雷諾數（Re）范圍內，不考慮側壁效應，流動主要表現為二維特征，因此建立了物理模型，如圖1所示。其中，臺階高度S=15mm，是定義Re的特征長度；流道高度H=2S，流道進口段長度L0=S，流道總長度L=101S；坐標原點位于臺階垂直面與底面的交點處，紅色壁面為被加熱面。該模型的邊界條件表達如下：

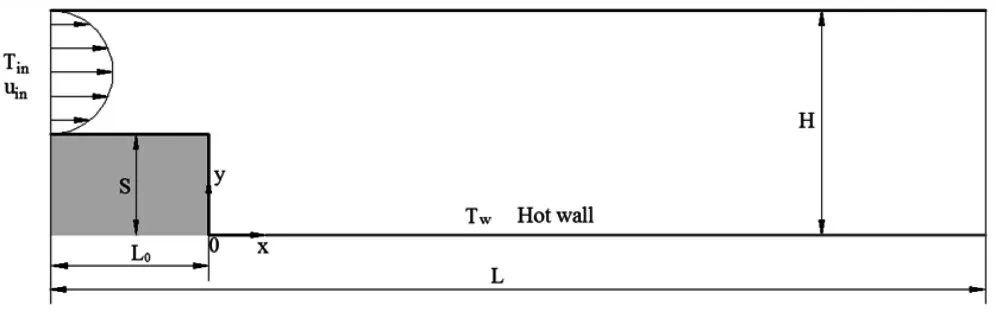
圖1 后向臺階繞流的物理模型Fig.1 Geometry Domains of the Backward-Facing Step

進口邊界，進口流向速度（uin）為充分發展，滿足拋物線分布，進口法向速度（vin）為0。進口處流體的溫度均勻分布Tin=283K。

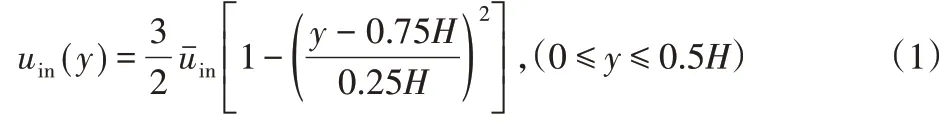
式中：uin—進口流向速度；y—坐標值；H—流道總高度。

出口邊界，流道出口處的速度場和溫度場符合邊界層近似理論。

[6][7][8][9][10][26][36][37][38][44][45][46][49][50][51][52]《馬克思恩格斯文集》(第1卷)，北京：人民出版社，2009年，第220、221、195、530、528、500、499、499、499、500、500、192、162、501、532、501頁。

壁面邊界，固體壁面均為無滑移邊界，被加熱面的溫度恒定為Tw=313K，其它壁面為絕熱邊界。

2.2 控制方程及求解方法

在這里的數值模擬研究中，做出了以下假設：流體為不可壓縮牛頓流體，流動為二維流動，流體物性值為常量。控制方程表達如下：

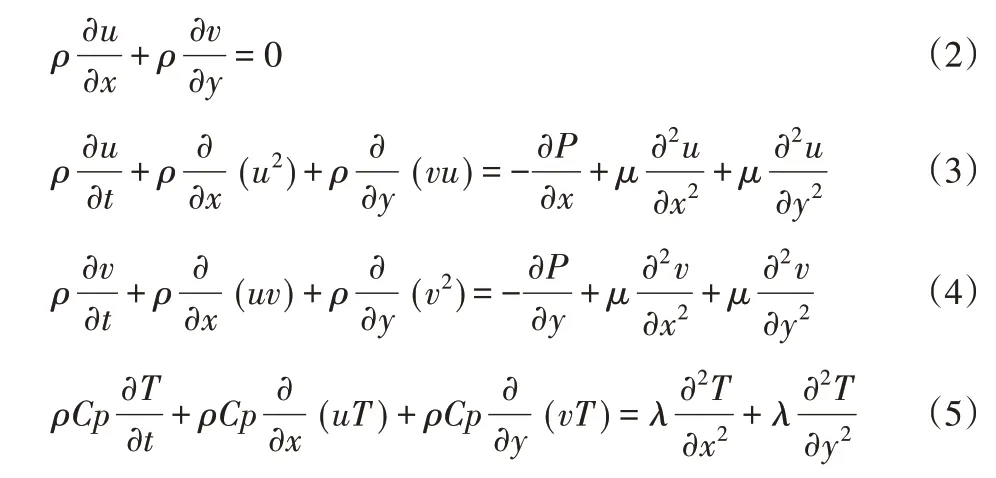
式中：式（2）是連續性方程，式（3）和式（4）是動量守恒方程，式（5）是能量守恒方程。其中，u、v、P和T分別代表x方向速度、y方向的速度，壓力和溫度。ρ、μ、λ和Cp分別代表流體密度，動力粘度，導熱系數和定壓比熱容，這些物性參數的取值：ρ=1.247kg·m-3、μ=1.76×10-5kg·m-1·s-1、λ=0.0251W·m-1·K-1和Cp=1.005 kJ·kg-1·K-1。

對于控制方程的求解，通過FORTRAN語言編程，采用有限容積法進行求解。QUICK格式用來離散對流項，ADI算法用來求解全隱式的差分方程。在每個時間步長里，進行反復迭代計算并采用SIMPLE算法進行速度壓力耦合修正。計算求解中，時間步長以最小網格為基準的Courant數等于1時的時間來定義。

2.3 網格無關性驗證及實驗驗證

這里選取后向臺階底面的時均努塞爾數（Num）來驗證網格無關性。Re=1000時臺階底面的Num，采用了4種不同的網格（網格雷諾數Reg分別設定為8、10、12、14）進行計算，如圖2所示。

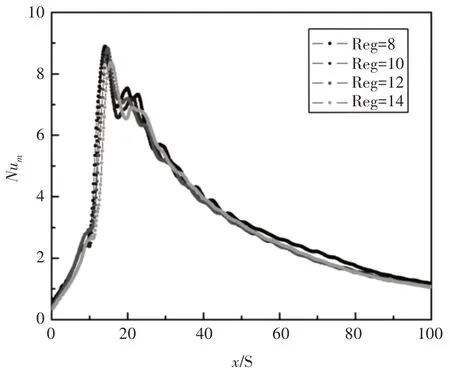
圖2 網格無關性驗證結果Fig.2 Grid Independence Test Results

通過對比發現，不同網格計算的結果均較為一致，這表明Reg≤12時網格已經能夠進行準確的計算。從保證計算結果準確性和提高計算效率兩方面考慮，這里選取Reg=12時的網格來進行數值模擬。

式中：ρ、μ流體—密度；動力粘度；Δxmin—最小網格間距；uin—進口流向速度。

在驗證了網格無關性的基礎上，將再附著點位置與已有的研究結果進行對比，發現模擬研究結果與文獻[18]的二維數值模擬結果吻合較好，與文獻[1]的實驗結果在Re大于400后出現了一定差異。存在該差異的原因可以歸結為：Armaly等的實驗在的三維流道內完成，存在固體側壁效應的影響。而本文為二維流動邊界條件，因此隨著Re的增大主回流區再附著點位置出現差異。

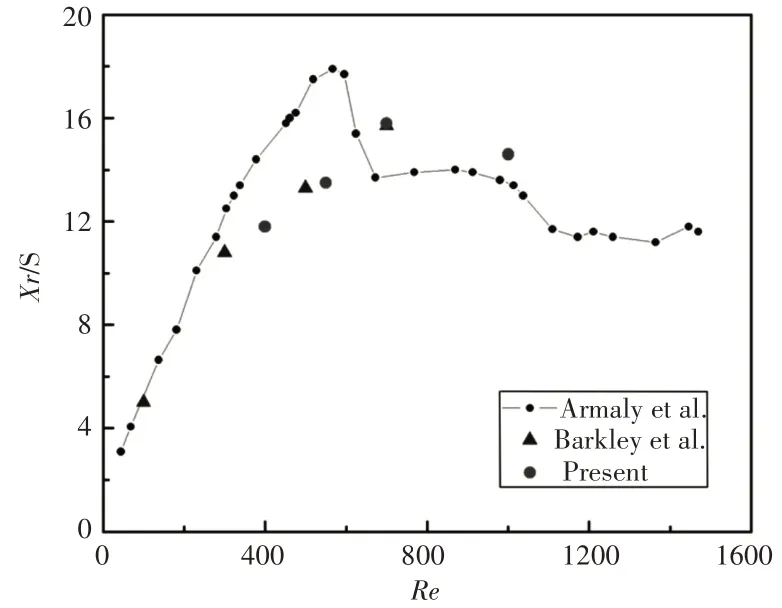
圖3 不同Re下后向臺階繞流再附著點位置Fig.3 Reattachment Length of the Backward-Facing Step Flow for Different Reynolds Numbers

這里還通過后向臺階閉式循環水槽實驗臺，結合PIV系統，開展實驗對典型工況的流動結果進行了驗證，如圖4所示。

圖4 閉式循環水槽實驗臺的實物圖Fig.4 Physical Map of the Closed Loop Water Tunnel

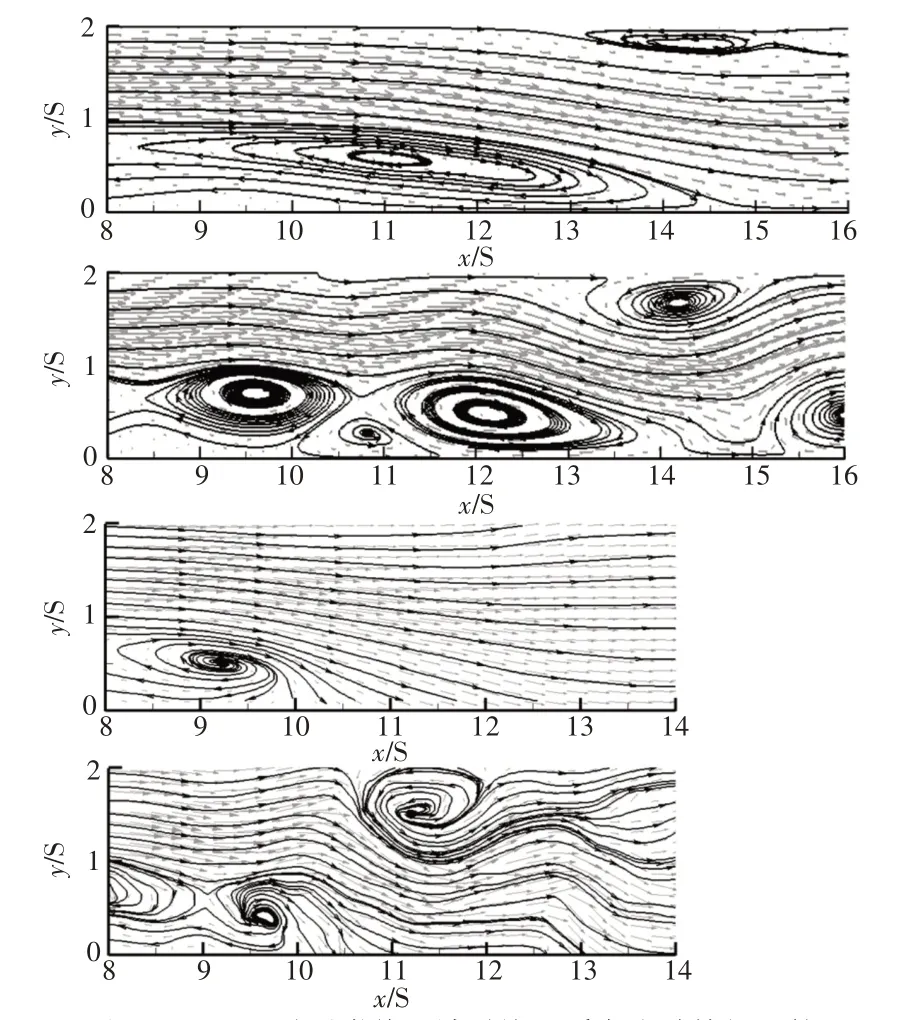
圖5 Re=1000時再附著區域時均及瞬態流動特征比較Fig.5 Time-Mean and Instantaneous Flow Characteristics in the Reattachment Region at Re=1000

3 結果與討論

3.1 時均流動傳熱特性

不同Re時后向臺階繞流臺階底面的時均努塞爾數和時均摩擦系數（Cfm）曲線，如圖6所示。

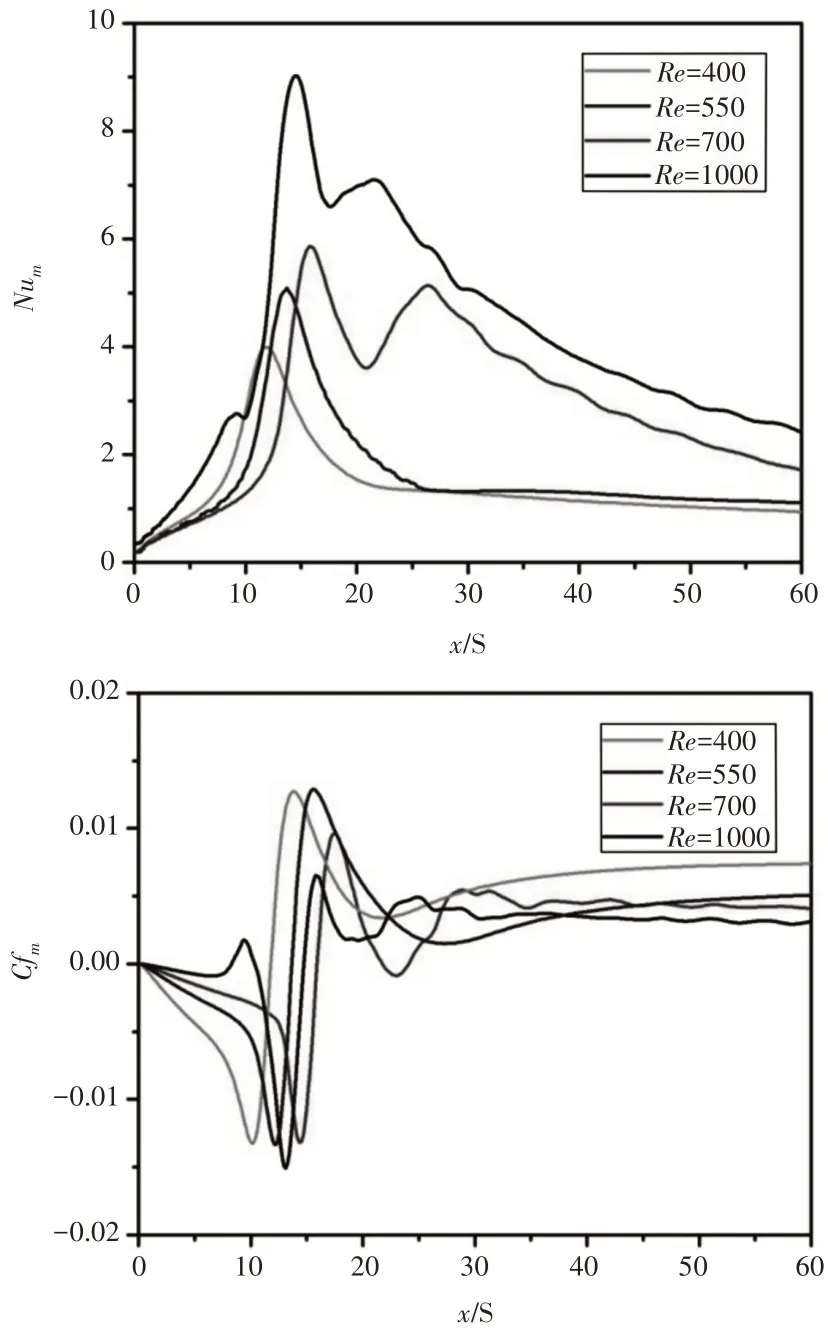
圖6 不同Re時臺階底面的時均努塞爾數和時均摩擦系數Fig.6 Distributions of Time-Mean Nusselt Number and Time-Mean Friction Coefficient for Different Reynolds Numbers

當Re=400 時，Num在再附著點附近形成一個峰值后迅速下降并趨于平穩。當Re=550時，Num曲線的變化趨勢與Re=400時相似，峰值有所增大，下游曲線平穩段Num的數值變化很小。隨著Re的繼續增大，在Re≥700后，Num曲線在再附著區域及其下游的傳熱相比Re=400和550時大幅提升，尤其是下游局部區域的增長超過3倍。而Cfm曲線在不同Re下的變化趨勢均較為相似，Re=700時的Cfm曲線相比Re=400和550時在再附著區有所下降，在下游區域相差不大。

以上流動傳熱現象表明：隨著Re的增大，流動從層流進入過渡流后，后向臺階繞流再附著區域及其下游產生了明顯的傳熱增強，且過渡流下局部區域的時均流動傳熱存在非相似性（Num增大時Cfm減小）。因此，過渡流下分離再附流動的強化傳熱機理值得深入分析，下文將對壁面強化傳熱的影響因素展開研究。

3.2 流動傳熱不穩定性的形成原因

為了理清過渡流下臺階底面再附著區域下游傳熱得到強化的原因，將Re=400與Re=1000時臺階底面的瞬時努塞爾數（Nu）曲線進行了比較，如圖7所示。當Re=400時，Nu曲線和Num曲線在不同位置均保持重合，再附著點附近形成單一峰值，再附著點下游的瞬態傳熱穩定，整體表現為典型層流傳熱特征。當Re=1000時，Nu曲線在臺階底面的各區域出現了不同程度的波動，其中再附著點下游局部區域的波動最為強烈，隨著向下游的推移，波動逐漸減弱。這表明在過渡流下，分離流體再附著后在下游流動中引發了明顯的流動傳熱不穩定性。

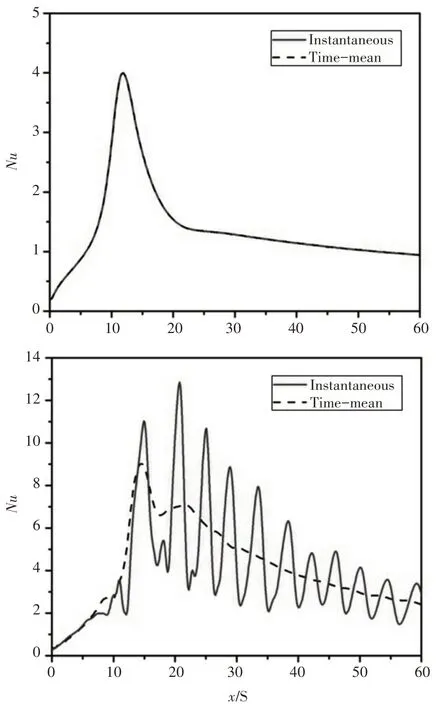
圖7 Re=400與Re=1000時臺階底面的努塞爾數Fig.7 Distributions of Nusselt number at Re=400 and Re=1000

進一步分析后向臺階繞流再附著點下游流動傳熱不穩定性的特征，Re=1000時后向臺階流道中兩個模擬點y方向速度（v）隨時間的變化特征，如圖8所示。圖8中速度數據計算所得的能量譜密度，如圖9所示。模擬點設置在再附著區域的下游，坐標分別為A（x/S=30，y/S=0.66）和B（x/S=40，y/S=0.66）。從圖8中可以看出，兩個模擬點的速度變化都表現出了較為規律的波動特征，為了確定波動的主頻率，需要結合模擬點速度的能量譜密度進行分析。

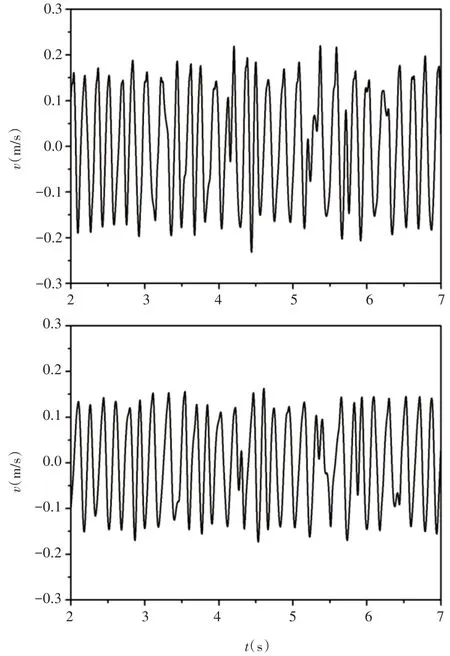
圖8 Re=1000時不同模擬點的y方向速度變化Fig.8 Velocity Component in y-Direction of Test Points at Re=1000

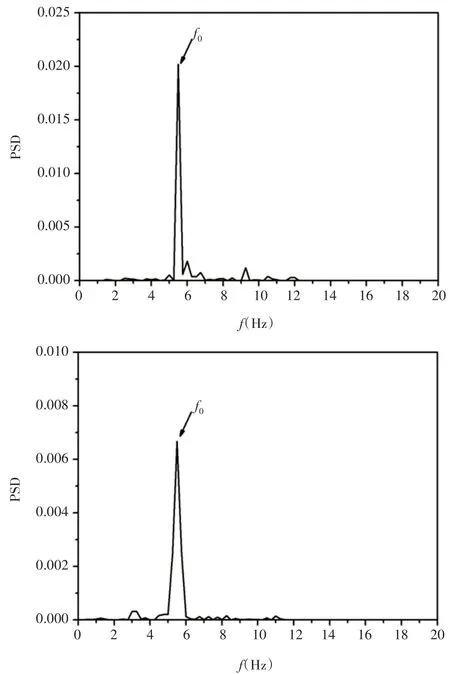
圖9 Re=1000時y方向速度的能量譜密度（由圖8的速度數據計算得到）Fig.9 Power Spectral Density of v at Re=1000（Calculated for the Data from Fig.8）

從圖9中可以看出，兩個模擬點y方向速度的能量譜密度均出現一個峰值，該峰值所對應的振動頻率都是5.5Hz，這表明Re=1000時后向臺階繞流在再附著點下游存在著振動主頻為5.5Hz的低頻脈動流動特征。

確定了過渡流下后向臺階繞流再附著點下游流動的低頻脈動特征后，在此基礎上，考察對應Re時再附著點下游的速度場和溫度場，如圖10所示。

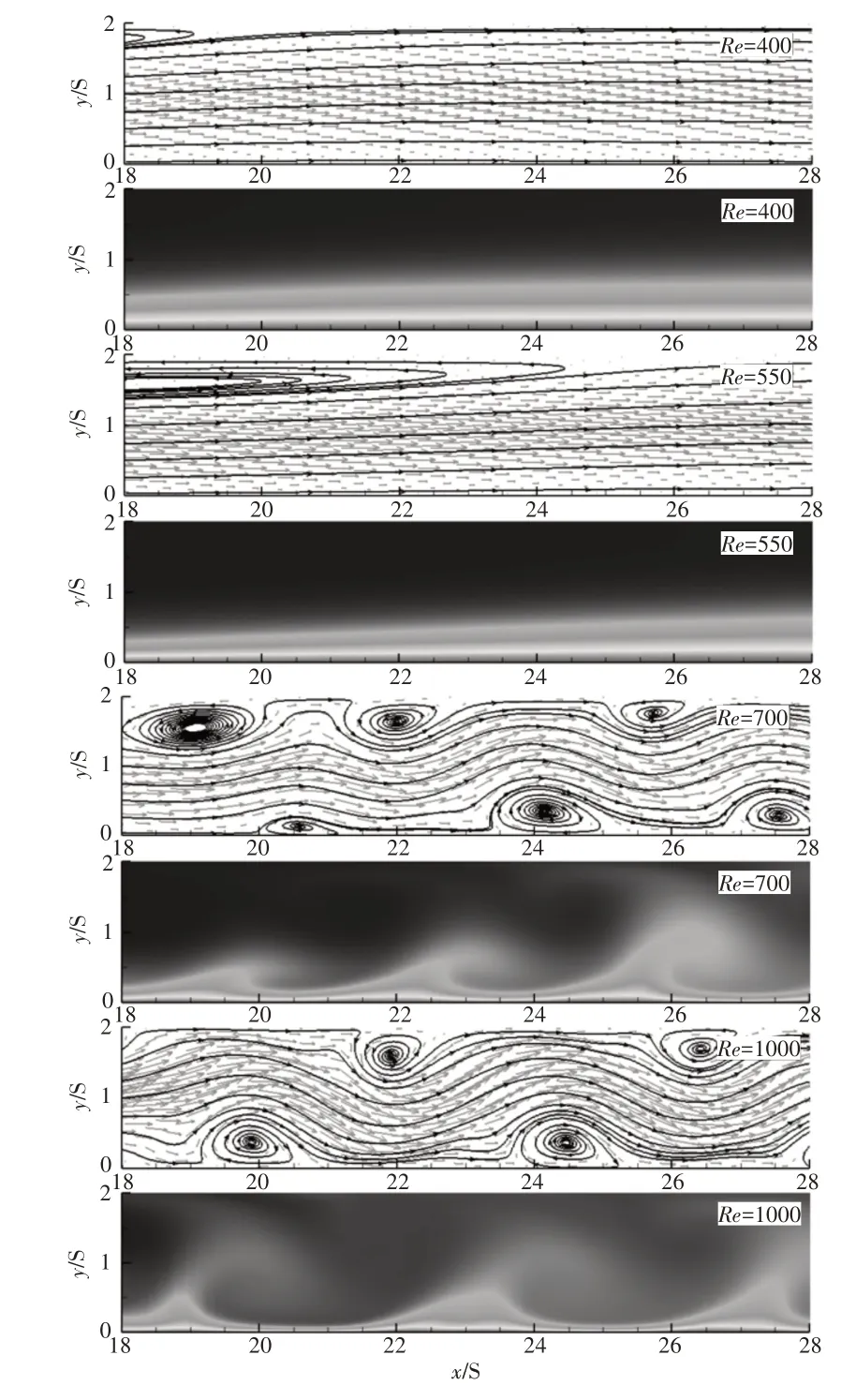
圖10 不同Re時再附著區域下游的瞬時速度場與溫度場Fig.10 Instantaneous Velocity and Temperature Fields Downstream of the Reattachment Region for Different Reynolds Numbers

從圖中可以看出，當Re=400時，再附著點下游的流動穩定，主流流動穩定，速度邊界層以及溫度邊界層內均為產生波動，整個流道內的溫度均勻分布，底面不同位置的溫度梯度變化不大。當Re=550時，整體流動形態及溫度分布與Re=400時相似，再附著區下游流動穩定，二次回流區的尺度有所增大，底面再發展的溫度邊界層厚度略有減薄。當Re=700時，再附著點下游的流動特征出現明顯變化，流道的上下壁面附近交替形成了多個旋渦。旋渦的形成促使主流產生明顯波動，流動表現出了不穩定性。伴隨流動不穩定性的形成，再附著點下游溫度邊界層不再穩定發展，產生了較強的溫度波動，表明近壁旋渦可以有規律地將主流的低溫流體引入至底面附近。當Re=1000時，整體上的流動結構相比Re=700時變化不大，流道壁面附近旋渦的形態略有變化，流體對壁面的沖擊角度增大。再附著點下游的溫度波動增強，冷流體與熱流體進一步混合，主流內的流體溫度明顯上升。

總體上，隨著Re的增大，再附著點下游從穩定流動轉變為非穩定流動，主要表現為流動進入過渡流（Re=700、1000）后，流道中上、下壁面附近交替形成近壁旋渦，并引起主流的波動。同時再附著區域下游溫度邊界層的發展也由穩定變為不穩定，該不穩定性的強度隨Re的增大而增強。

4 結論

這里對層流到過渡流狀態下后向臺階繞流的流動傳熱特性進行了研究，重點分析了主回流區再附著點下游的低頻脈動特性及其對壁面傳熱的影響。主要得到以下結論：

（1）當流動從層流進入過渡流后，后向臺階繞流主回流區再附著點下游形成區域性的強化傳熱，局部范圍內的傳熱提升超過3倍，且該區域的流動傳熱產生非相似性。

（2）后向臺階繞流再附著點下游的流動出現了明顯的低頻脈動特征，該流動不穩定性誘導流體在上、下壁面附近交替形成旋渦。這些旋渦的準周期性運動是強化底面傳熱的直接原因。

（3）強化傳熱的具體特征可以歸結為：從Re=400到Re=700，低頻脈動特性誘導的旋渦運動破壞了底面的速度邊界層，同時加強了冷熱流體的混合，從而形成了區域性的強化傳熱。從Re=700到Re=1000，旋渦形態的變化，促使旋渦運動沖擊底面的角度增大，近壁的低速回流區域減小，因此傳熱產生進一步的增強。