利用車輛狀態估計的客車防側翻控制

康小鵬，董 浩，祁傳琦，王 輝

（1.成都大學機械工程學院，四川 成都 610106；2.成都大學高等研究院，四川 成都 610106）

1 引言

近年來，我國客車在重大交通事故中的占比較高，這類事故往往造成群死群傷的嚴重后果，客車的事故形態中，側翻是危害較大的一種，約占重大事故總數一半[1]。據美國公路交通安全管理局（NHTSA）2013年統計數據表明：美國有568.7萬車次交通事故，汽車側翻事故僅占1.7%，但汽車側翻傷亡人數占交通事故總傷亡人數的19.1%，且大部分來自客車側翻事故。汽車側翻大體上可分為兩類：一類是由曲線運動時汽車過大的側向加速度引起；另一類是由汽車行駛時產生側向滑移后與路面障礙物的側向撞擊所致，稱為絆倒側翻[2]。由于絆倒側翻具有隨機性、難預測、難控制等特征，很難對其進行有效的主動防范，所設計的主動防側翻控制系統只針對第一類側翻。

目前，汽車主動防側翻控制的方法主要有差動制動控制[3]、主動懸架控制[4]、主動轉向控制（AFS）[5]以及主動防側傾穩定桿控制[6-7]。主動懸架控制由于成本高、結構復雜，目前實際應用較少。而主動防側傾穩定桿雖然結構簡單，但其結構功能相對獨立，不便于汽車現有穩定性控制系統集成。差動制動由于可以利用目前比較成熟的汽車動力學控制系統（VDC）進行集成，在不額外增加硬件負擔的情況下只需要對上層控制器進行設計，因此具有很強的實用價值和廣泛的應用前景[8]。

2 整車三自由度側翻模型

為設計主動防側翻控制器，需要建立客車的整車數學模型。考慮到研究對象為中小型客車，其非簧載質量通常較小，對車輛的側翻影響權重較小，在綜合分析計算精度和運算效率后建立包含側向、橫擺、側傾運動的三自由度整車模型[9]。三自由度參考模型，如圖1所示。

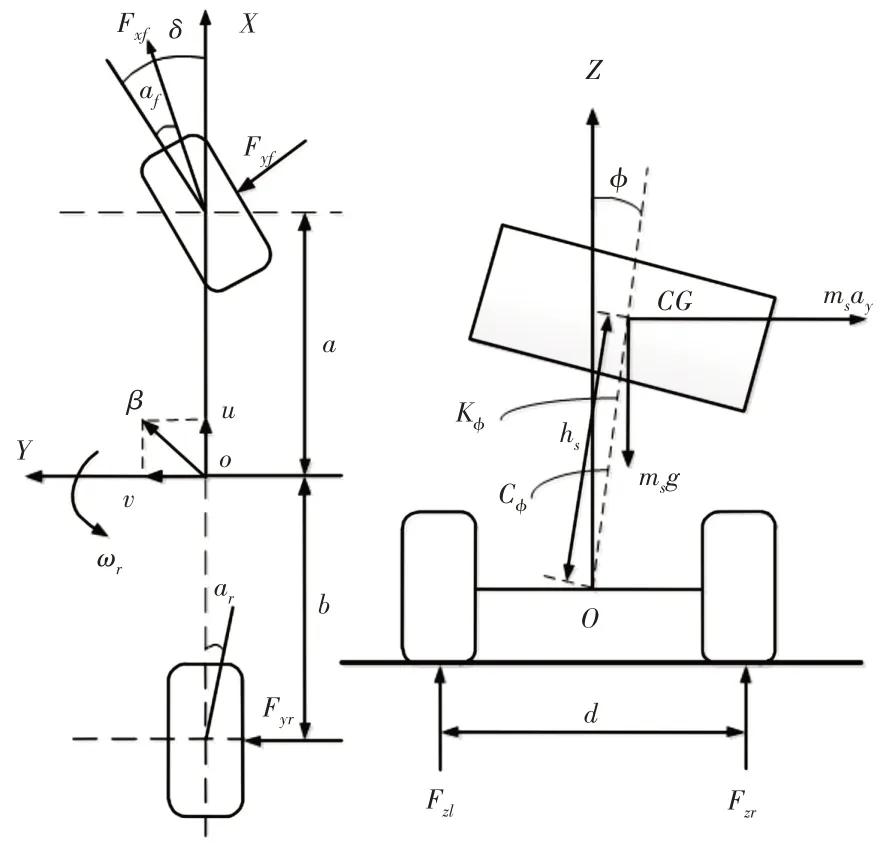
圖1 三自由度參考模型Fig.1 3-DOF Reference Model

圖中：ms—車輛簧載質量；ay—車輛側向加速度；?S—車輛簧載質量側傾中心到質心的距離；φ—車輛側傾角；Fxf、Fxr—車輛前后輪所受到的縱向力；Fyf、Fyr—車輛前后輪所受到的側向力；Fzf、Fzr—車輛左、右車輪的垂向載荷；δ—車輛前輪轉向角；β—車輛質心側偏角；u—車輛縱向速度；v—車輛側向速度；αf、αr—車輛前、后輪輪胎側偏角；ωr—車輛橫擺角速度；a、b—車輛質心到前后軸的距離；d—輪距；Cφ—車輛等效側傾角阻尼系數；Kφ—車輛等效側傾角剛度；g—重力加速度。

將上述三個方向的動力學方程寫成狀態空間方程，如式（1）所示，即：

式中：A—模型固有參數矩陣；B—輸入矩陣；x—狀態向量。

式中：Ix—車輛簧載質量繞側傾軸的轉動慣量；

Iz—車輛繞Z軸的轉動慣量；

Ixeq—車輛簧載質量繞X軸的等效轉動慣量；

Cf、Cr—車輛前后輪總側偏剛度。

3 側翻工況判定

3.1 側翻指標選擇

目前車輛側翻的判定指標主要有靜態穩定因子（SSF）、穩定裕度（SM）、橫向載荷轉移率（LTR）和側翻時間（TTR）等[10-11]，選擇橫向載荷轉移率（LTR）作為側翻判定因子，其計算表達式如下：

式中：DLTR—LTR計算值，滿足DLTR∈[-1，1]。

由LTR定義可知，當有一側車輪的垂向載荷為0時，即Fzl=0或Fzr=0時，車輛將發生側翻。受限于傳感器技術和測量難度等因素，DLTR無法直接觀測，通常利用車輛本身傳感器進行間接測量。對式（6）進一步展開，忽略前后輪輪距差、非簧載質量，并假定客車處于小側傾角范圍，以圖1中側傾中心為參考點列力矩平衡方程。

式中：m—整車質量，將式（7）～式（11）式帶入式（6）可得：

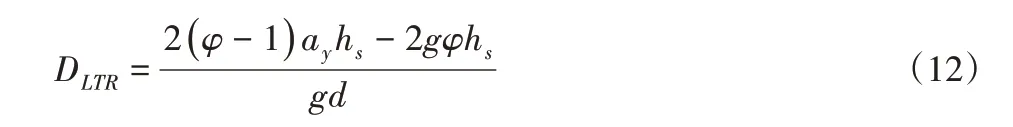
根據式（12）可知：DLTR只與車輛的結構參數和行駛狀態參數相關，結構參數車輛出廠時已知，動態變化的只有側向加速度和車身側傾角。

3.2 橫向載荷轉移率計算

考慮到行駛狀態參數測量的精度和難度，采用UKF的方法對車輛行駛狀態參數進行估計。

根據建立的三自由度車輛模型，定義系統狀態變量X()

t=；定義系統量測變量為Z(t)=[φ ay]；輸入變量為u(t)=[δ]。在任意時刻t，非線性系統均可由狀態變量X和觀測變量Z（t）表示，即：

式中：f—狀態轉移函數；h—量測函數；w（t）、v（t）—零均值高斯白噪聲，其協方差陣分別為Q，R。

使用UKF算法對車輛狀態參數估計步驟如下。

（1）UKF 使用無跡變換（Unscented Transform，UT）來處理均值和協方差的非線性傳遞問題。其本質是對非線性函數的概率密度分布進行近似，用一系列確定樣本來逼近狀態的后驗概率密度，不要需要對雅克比矩陣進行求導，對非線性分布的統計量具有較高的計算精度[12]。UT變換的實現方法如下：

式中：n—狀態變量的維數；、P—變量的均值和方差；下標m—均值；c—協方差；上標—第幾個采樣點；λ—縮放比例參數，作用是降低總的預測誤差。其計算公式如下：

根據式（14）和式（15）獲得一組采樣點（稱為Sigma點集）及其對應權值。

（3）計算系統狀態變量的一步預測及協方差陣，它由Sigma點集的預測值加權求和得到，權值ω(i)通過式（15）獲得：

（4）根據一步預測值，再次使用UT變換，產生新的Sigma點集。

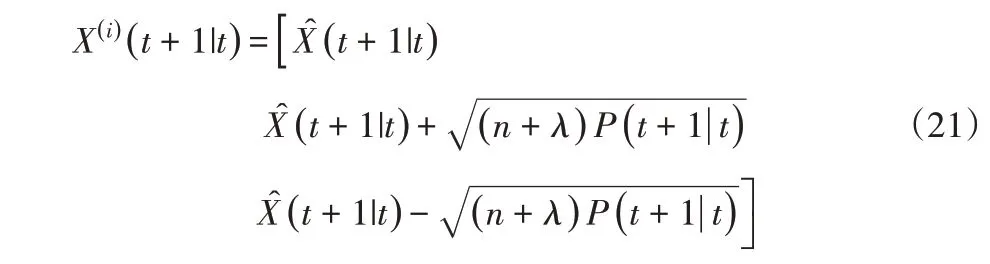
（5）將式（21）預測的Sigma點集帶入觀測方程，得到預測的觀測量，i=1，2，…，2n+1。

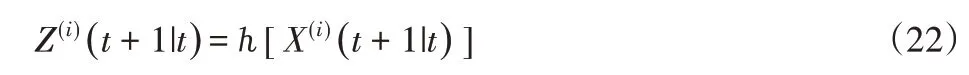
（6）對式（22）得到的觀測預測值，通過加權求和得到系統預測的均值及協方差：

（7）計算卡爾曼增益矩陣：

（8）更新系統的狀態和協方差：

4 防側翻控制器設計

該控制策略分為4個模塊：三自由度參考模型、UKF估計器、側翻工況判定、側翻控制，控制原理，如圖2所示。

圖2 控制原理圖Fig.2 Control Schematic Diagram

三自由度參考模型接受車輛縱向車速及前輪轉角信號后計算理論車身側傾角；UKF估計器對車輛行駛過程的狀態參數進行估計后用于側翻工況的判定；選擇0.85作為橫向載荷轉移率絕對值的閾值，側翻工況判定模塊在識別側翻工況為真以后，計算出控制需要的補償橫擺力矩；側翻控制模塊根據計算的補償橫擺力矩和前輪轉向的符號選擇施加差動制動的車輛并計算制動輪缸壓力。

采用柔性PID控制算法對側翻控制最優補償橫擺力矩進行決策，并通過差動制動的方式實現，補償橫擺力矩的計算過程，如圖3所示。

圖3 補償橫擺力矩計算流程圖Fig.3 Flow Chart of Compensation Yaw Moment Calculation

補償橫擺力矩的計算公式為：

式中：eφ—側傾角差；Kp0—初始比例系數；Ti0—初始積分時間常數；Td0—初始微分時間常數。

執行器對制動車輪的選擇根據橫向載荷轉移率的數值范圍實施，其具體情況，如表1所示。

表1 制動車輪選擇策略Tab.1 Selection Strategy of Braking Wheel

5 仿真驗證

防側翻控制系統的開發需要大量的試驗數據支撐，考慮到汽車側翻是一種非常危險的工況，選擇Trucksim作為驗證平臺，建立整車動力學模型，并在Matlab/Simulink中建立控制器模型和理論參考模型。整車參數，如表2所示。

表2 整車主要參數Tab.2 Main Vehicle Parameters

選擇魚鉤試驗（Fish Hook Test）對所設計的控制器的有效性進行驗證。試驗車速為55km/h和80km/h，方向盤轉角，如圖4所示。

圖4 魚鉤試驗方向盤轉角Fig.4 Steering Wheel Angle of Fish Hook Test

55km/h魚鉤試驗結果，如圖5所示。

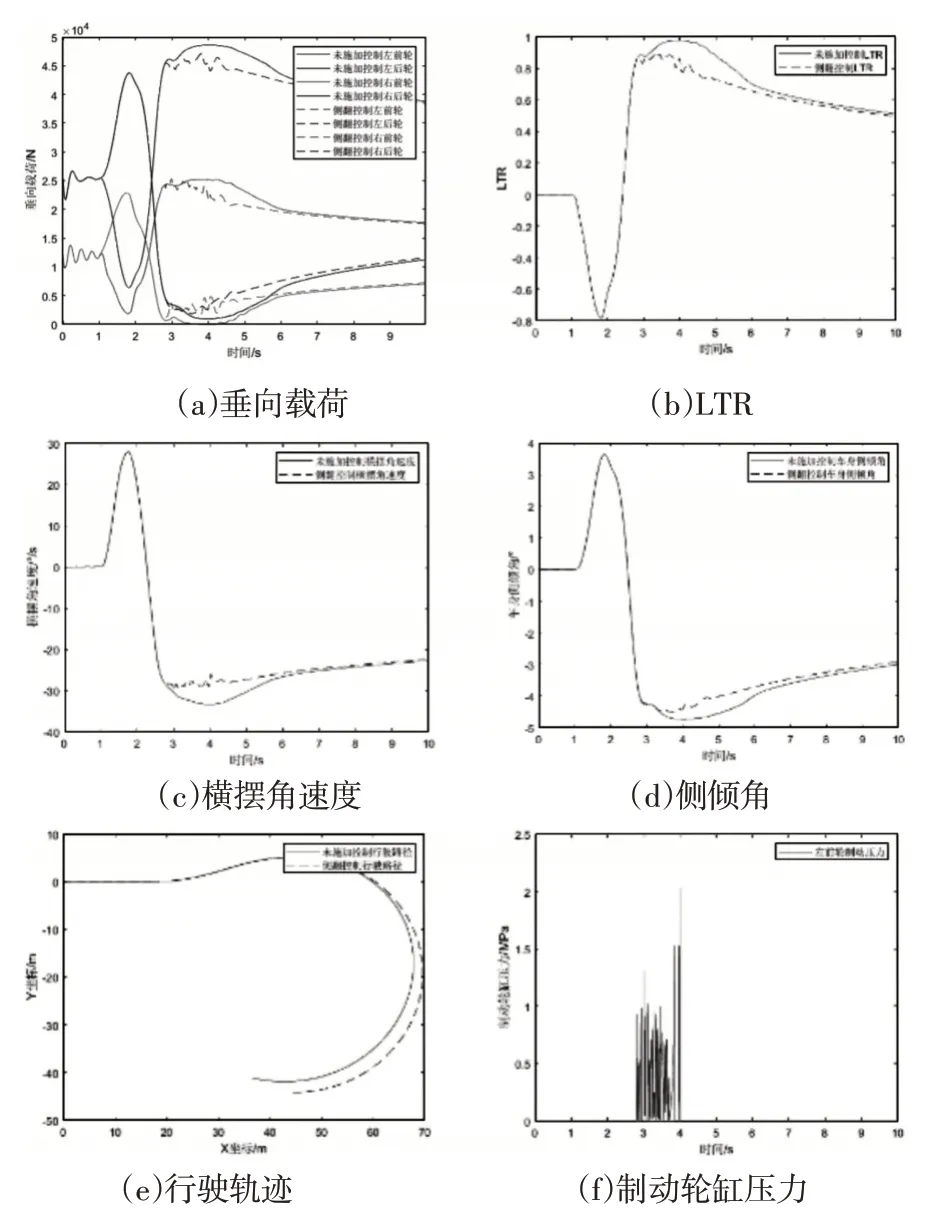
圖5 55km/h試驗結果Fig.5 55km/h Test Results

由圖5可以看出，未施加控制時，車輛在運行2.8s時LTR值已經達到側翻閾值0.85，右前輪載荷降低至初始載荷46.3%，右后輪載荷降低至初始載荷32.3%；車輛在運行4.0s時LTR值達到最大的0.97，右前輪載荷已經降低至初始載荷0%，右后輪載荷降低至初始載荷3.7%，車輛即將發生側翻。通過施加主動防側翻控制后，LTR最大值降低了20.1%，始終處于安全閾值0.85以下，側傾角最大值降低了12.3%，確保車輛始終處于穩定狀態。

80km/h魚鉤試驗結果，如圖6所示。

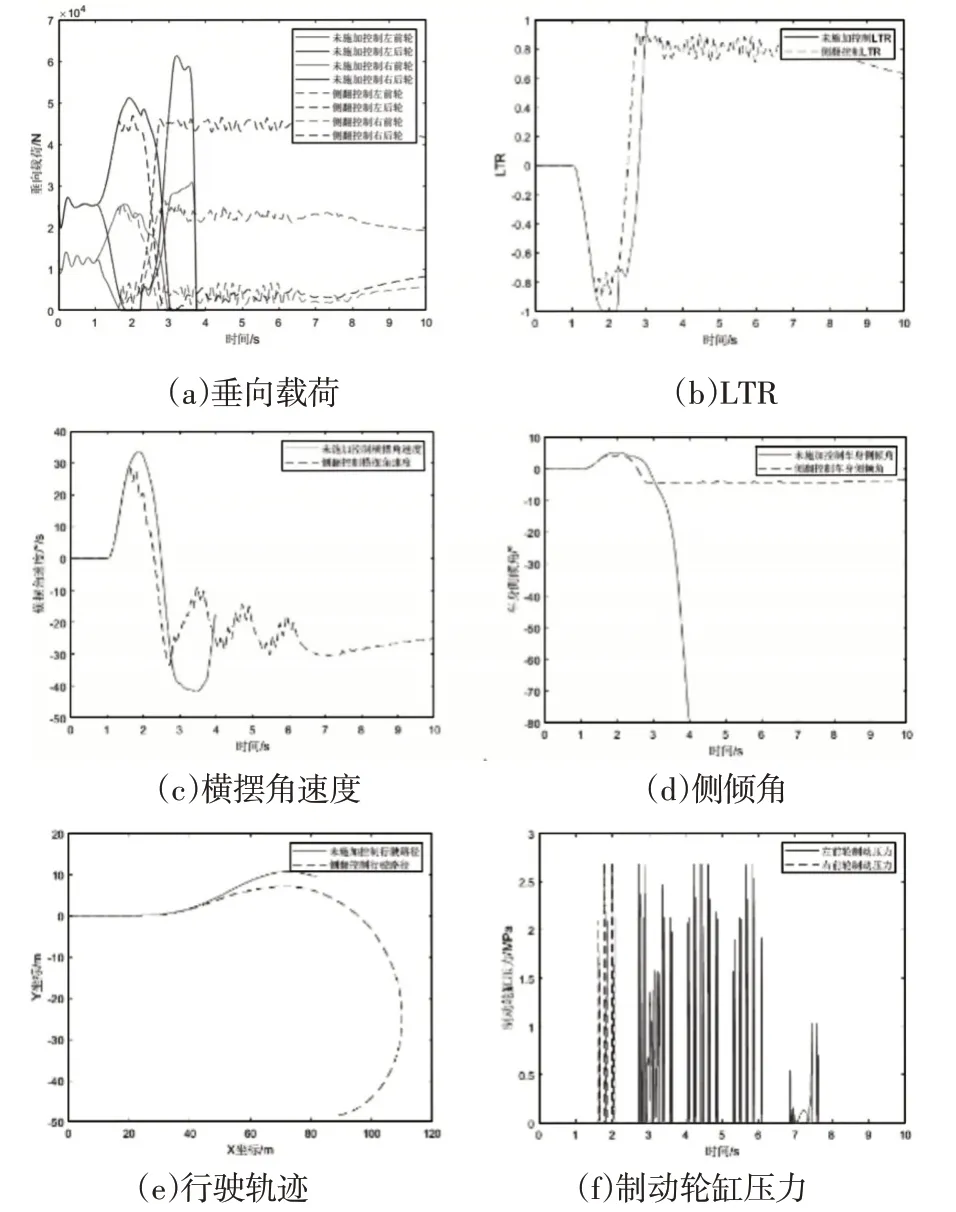
圖6 80km/h試驗結果Fig.6 80km/h Test Results

由圖6可以看出，未施加控制時，車輛在運行1.6s時LTR值已經達到側翻閾值-0.85，在0.2s后LTR值達到極限值-1，雖然汽車未發生側翻，但此時右側車輪已完全脫離地面，垂向載荷降低至0，處于非常危險的工況；車輛在運行2.9s時LTR值達到側翻閾值0.85，在0.1s后LTR值達到極限值1，在運行至3.7s時車輛發生側翻事故。施加主動防側翻控制后，左轉向時LTR 最大值降低到-0.88，右轉向時LTR 最大值降低到0.86，始終處于安全閾值0.85附近震蕩，車身側傾角控制在4.5°以內，確保車輛始終處于穩定狀態。

6 結論

針對以LTR為側翻判定因子的主動防側翻控制中狀態參數獲取困難的問題，基于無跡卡爾曼濾波原理設計了車輛狀態參數估計器，對車輛行駛過程中的LTR值進行了實時估計；基于直接橫擺力矩控制的原理設計了柔性PID主動防側翻控制器，并通過差動制動對附加橫擺力矩進行補償。選擇魚鉤試驗在兩種車速下對設計的控制系統進行了仿真分析，結果表明，在中、高車速下，對LTR值和側傾角的控制均有非常好的效果，且對車輛的預期行駛狀態干預較小，能夠有效的提高客車的側翻穩定性。