柔性薄壁軸承的周期性沖擊背景特性及其分離

趙學智，葉邦彥，陳統堅

（華南理工大學機械與汽車工程學院，廣東廣州 510641）

引言

柔性薄壁軸承是諧波減速器的重要部件。諧波減速器具有傳動比大、傳動精度高、傳動效率高、體積小等優點，被廣泛應用于空間飛行器、工業機器人、雷達設備以及醫療設備等器械的傳動系統中［1-2］。諧波減速器的核心元件之一是柔性薄壁軸承，與普通滾動軸承相比，柔性薄壁軸承內外圈的壁厚很薄且具有較大的韌性和彈性，這種軸承裝配在橢圓凸輪上，內、外圈發生彈性變形成為橢圓，因此它是一個橢圓軸承。在諧波減速器中，柔性薄壁軸承的外圈上裝有帶外齒的柔輪，它與帶有內齒的剛輪相嚙合，當橢圓凸輪旋轉時，凸輪周期性擠壓柔性薄壁軸承以及柔輪，使得柔輪的外齒與剛輪的內齒周期性地嚙合和脫開，實現將旋轉運動從橢圓凸輪軸傳遞到剛輪［1-2］。柔輪的齒數比剛輪的齒數少兩個，橢圓凸輪旋轉一周，柔輪與剛輪的相對位移為其齒差所對應的角度，因此諧波減速器可以獲得很高的單級減速比。

柔性薄壁軸承介于橢圓凸輪與柔輪之間，是諧波減速器傳遞動力的關鍵部件，它與普通滾動軸承的典型區別是：它的內、外圈是橢圓，這使得它的振動具有非常獨特的特點。目前對于柔性薄壁軸承的研究主要是關于其疲勞壽命分析［3］、內外圈應力-應變以及載荷分布規律［4］、軸承結構參數對柔性軸承變形及應力的影響［5］以及軸承元件制造誤差對柔性薄壁軸承和柔輪之間的應力影響［6］等方面的研究，而對這種軸承的振動分析和故障診斷的研究較少。目前只有Adams 等提出了一種橢圓軸承的有限元振動模型［7］，但是他們只是對橢圓軸承的振動進行有限元數值模擬分析，沒有對此類軸承進行實際振動檢測。筆者對這種特殊軸承的振動進行了實際檢測和分析，結果表明Adams 等的這種有限元模擬分析結果并不準確。實際振動檢測結果表明，在健康的柔性薄壁軸承的振動中，存在著一種周期性沖擊，經研究發現這種沖擊是由于橢圓長短軸的旋轉造成的，這和普通滾動軸承完全不同，普通軸承只有在損傷后才會出現周期性沖擊，而當柔性薄壁軸承損傷后，這種正常的周期性沖擊和故障引起的周期性沖擊混合在一起，形成一種復雜的沖擊信號，對柔性薄壁軸承的故障周期性沖擊特征是一個極大的干擾。本文分析了這種正常周期性沖擊的頻率分布特點，為了消除這種正常的周期性沖擊對故障沖擊特征提取的影響，提出利用奇異值分解方法將柔性薄壁軸承正常的周期性沖擊從原始振動信號中分離出來，從而消除其對故障周期性沖擊的干擾。在消除正常周期性沖擊的影響后，采用連續Morlet 小波變換對故障周期性沖擊進行提取，通過最大峭度確定最佳小波尺度。信號處理結果表明，SVD 能準確分離出柔性薄壁軸承振動信號中的正常周期性沖擊，改善Morlet 小波對柔性薄壁軸承故障周期性沖擊特征的提取效果。

1 實驗裝置和設備

針對柔性薄壁軸承的特點，設計了專門的柔性薄壁軸承振動檢測試驗臺，其原理如圖1所示，其中柔性薄壁軸承安裝在高精度橢圓凸輪軸上。因為柔性薄壁軸承的內外圈都很薄，且有很大的韌性和彈性，裝在橢圓凸輪軸上后，其內外圈發生彈性變形，被脹成橢圓。橢圓凸輪軸由電主軸驅動，其轉速非常穩定。檢測臺還設計有徑向力加載機構，便于在檢測時對柔性薄壁軸承施加徑向壓力。PCB 加速度計安裝在徑向加載塊上，振動信號由LMS 數據采集系統采集。試驗臺實物如圖2所示。

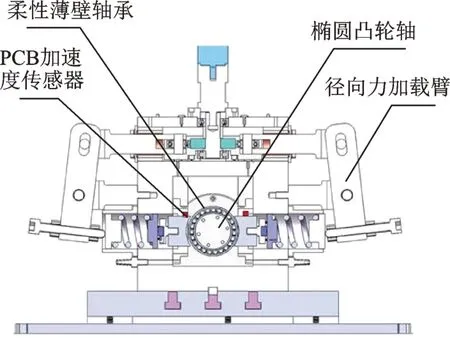
圖1 柔性薄壁軸承振動檢測試驗臺原理Fig.1 Principle of vibration detection bench of flexible thinwall bearing

圖2 柔性薄壁軸承振動檢測試驗臺Fig.2 Vibration detection bench of flexible thin-wall bearing

本文實驗中檢測的柔性薄壁軸承型號為SHF-32-120，其主要參數如表1所示。

表1 型號為SHF-32-120 的柔性薄壁軸承參數Tab.1 Parameters of flexible thin-wall bearing with type SHF-32-120

2 健康柔性薄壁軸承周期性沖擊特性

首先對一個健康柔性薄壁軸承的振動進行檢測，檢測時橢圓凸輪軸的轉速為750 r/min，即轉頻為12.5 Hz，采樣頻率為6400 Hz，采樣點數為4096點，檢測到的振動加速度信號及其頻譜如圖3所示。

圖3 健康柔性薄壁軸承的振動信號及其頻譜Fig.3 Vibration signal of healthy flexible thin-wall bearing and its spectrum

從圖3 可見振動信號中存在著非常明顯的周期性沖擊，但是需要注意的是：這是一個健康的柔性薄壁軸承。對于普通滾動軸承來說，只有在滾道或滾動體損傷后才會產生周期性沖擊，健康的普通軸承振動信號中不存在周期性沖擊，而圖3 的結果表明，健康的柔性薄壁軸承中卻存在周期性沖擊，可見柔性薄壁軸承具有非常獨特的振動特性，和普通滾動軸承完全不同。從圖3 的頻譜可見原信號在頻域表現為一系列等間隔的頻率成分。這種時、頻域特征是周期性沖擊的典型特征，對于理想的周期性沖擊∑δ（t-nT）（其中T為沖擊的周期），其在頻域是一系列等間隔的譜線（1/T）∑δ（f-n/T）。因為這是健康的柔性薄壁軸承，因此把這種沖擊稱為柔性薄壁軸承的正常周期性沖擊。由圖3 可知，這種正常周期性沖擊的基頻是25 Hz，這正好是轉頻12.5 Hz 的兩倍，而頻譜中的其他頻率是基頻25 Hz 的一系列倍頻，圖3 中顯示出了其1～13 階的倍頻。

正常周期性沖擊的基頻是轉頻的兩倍這一現象不是偶然的，結合柔性薄壁軸承的特點，可知健康柔性薄壁軸承振動信號中的周期性沖擊是橢圓的長、短軸造成的。因為柔性薄壁軸承內外圈是橢圓，隨著內圈橢圓的旋轉，橢圓長軸經過加速度計時，加速度計會受到一次向外的沖擊，短軸經過加速度計時，加速度計會受到一次向內的沖擊，方向與長軸的沖擊方向相反。凸輪旋轉一轉，長軸經過加速度計兩次，因此長軸引起的沖擊頻率是轉頻的兩倍，短軸也經過加速度計兩次，其引起的沖擊頻率也是轉頻的兩倍。給出凸輪軸旋轉一轉時軸承受到的沖擊，如圖4所示（凸輪軸旋轉一轉的時間是1/12.5 Hz=0.08 s），可見在一轉之內存在四個沖擊，其中兩個沖擊是長軸引起的，兩個沖擊是短軸引起的，長軸和短軸引起的沖擊方向相反，二者交替出現，其頻率都是轉頻的兩倍。在文獻［7］中，Adams 等通過有限元數值模擬方法分析了橢圓軸承的振動，他們的模擬結果表明健康橢圓軸承的振動中存在正沖擊和負沖擊，這和本文作者的實測結果相符合，但是Adams等認為正沖擊和負沖擊的頻率與圓形軸承的故障特征頻率一致［7］，但作者的實測結果表明，健康橢圓軸承振動信號中正、負沖擊的頻率都是轉頻的兩倍，這種實測結果表明文獻［7］的有限元數值模擬結果并不準確。

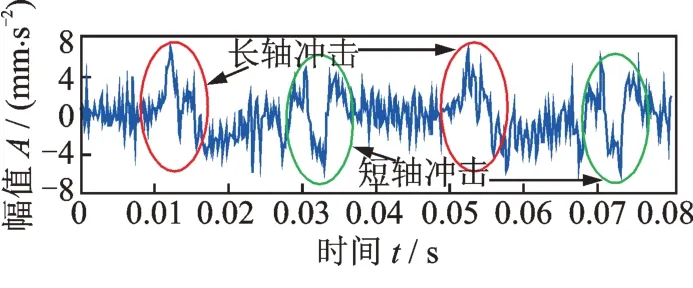
圖4 凸輪軸旋轉一轉時柔性薄壁軸承受到的沖擊Fig.4 Impacts on flexible thin-wall bearing when camshaft rotates one revolution

因為健康柔性薄壁軸承的振動信號中存在周期性沖擊，而當柔性薄壁軸承損傷后，滾動體經過損傷點也會引起周期性沖擊，正常周期性沖擊和損傷周期性沖擊混在一起，構成了一種非常復雜的沖擊信號。對于普通滾動軸承而言，其內外圈是圓形，所以不會產生正常周期性沖擊，不存在需要消除正常周期性沖擊的問題，但柔性薄壁軸承完全不同，橢圓長短軸產生的正常周期性沖擊較強烈，掩蓋了損傷周期性沖擊，因此在故障軸承的振動信號中必須設法消除這種正常周期性沖擊。

3 SVD 分離正常周期性沖擊的原理

奇異值分解是一種矩陣分解方法，近年來在信號消噪中有很多的應用。對一個實際采集到的柔性薄壁軸承振動信號［x（0），x（1），…，x（N-1）］，N為信號長度，為了對它進行奇異值分解，首先需利用這個振動信號構造如下矩陣［8-9］：

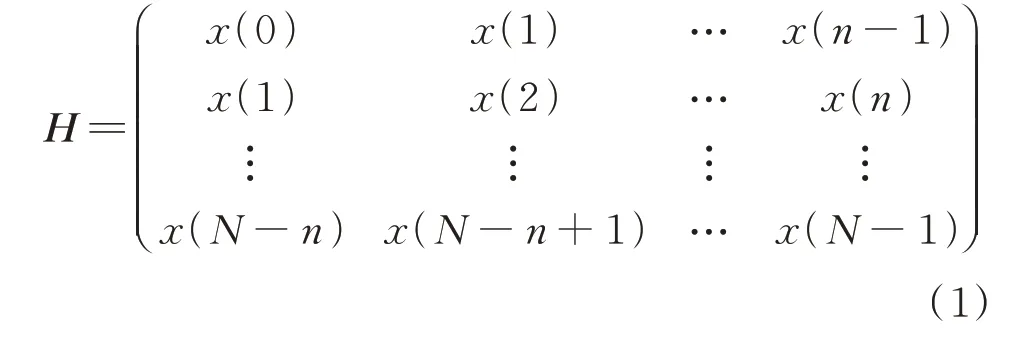
式中 1＜n＜N。令m=N-n+1，則H為一個m×n的矩陣，此矩陣又稱為Hankel 矩陣［10-11］。對柔性薄壁軸承振動信號構造的矩陣H進行SVD 分解，得到：

式中U為一個m×m的單位正交矩陣，V為一個n×n的單位正交矩陣，D為一個m×n的對角矩陣。當m＜n時，D=[diag(σ1，σ2，…，σq)，0]；當m＞n時，D=[diag(σ1，σ2，…，σq)，0]T，0 表示零矩陣。q=min（m，n），且σ1≥σ2≥…≥σq≥0，它們是矩陣H的奇異值，也是信號x（i）的奇異值。

在信號處理中，SVD 一般是用來消噪的，SVD的消噪結果波形失真小，無相移，對機械振動信號［12-13］、磁共振信號［14］、生物醫學信號［15-16］等不同性質的信號都有很好的消噪效果。但是SVD 除了消噪外，還可以提取原始信號中任意的單個或多個頻率成分，這一特性源自于信號中頻率和奇異值的一種內在聯系［17］。由文［17］發現，利用原始信號x（i）構造Hankel 矩陣，當矩陣維數q大于原始信號中頻率數量的兩倍時，原始信號中的每一個頻率成分將產生而且只產生兩個非零奇異值，利用某個頻率成分對應的兩個非零奇異值進行SVD 重構，可以分離出這個頻率成分［17］。在實際構造Hankel 矩陣時，對于確定的信號長度N，應使矩陣維數q最大［12］。由式（1）可見，原信號構造的Hankel 矩陣行數和列數存在約束關系m=N-n+1，當行數m增大時，列數n將變小，而矩陣維數q=min（m，n）。為了使q最大，如果信號長度N為偶數，取行數m=N/2+1、列數n=N/2 來構造Hankel 矩陣，此時q可取到最大值N/2；如果N為奇數，取行數m=（N+1）/2、列數n=（N+1）/2 來構造Hankel 矩陣，此時q可取到最大值（N+1）/2。實際處理信號的長度N一般至少為512，這樣矩陣維數q至少為256，一般會大于原始信號中頻率數量的兩倍。

而為了分離出信號中一個具體的頻率成分，必須選擇出這個頻率對應的兩個奇異值。設原始信號x（i）是通過采樣周期Ts得到的，對x（i）構造的m×n的Hankel 矩陣進行SVD 分解，設x（i）中的頻率分量ajsin(ωjTsi+φj)對應的兩個奇異值是σk和σk+1，可以證明，這兩個奇異值的平方和與頻率分量ωj的參數存在下面的關系：

式中aj為頻率ωj的幅值，φj為相位，m×n為矩陣階數，Ts為原始信號的采樣周期。對于確定的矩陣階數和采樣周期，由式（3）可見，頻率分量ωj產生的兩個奇異值的能量與ωj的幅值aj的平方成正比，幅值aj越大，則ωj對應的兩個奇異值也越大，此外頻率值ωj及相位φj也對奇異值的大小有一定影響，但幅值的影響是最大的［18］。在實際中，通過對x（i）做頻譜分析，可以獲得幅值aj、頻率值ωj和相位φj，則可以利用式（3）計算頻率分量ωj對應的兩個奇異值的能量和。這樣可以計算原始信號x（i）各個頻率的奇異值能量和，因為奇異值序列是降序排列的，如果頻率分量ωj的奇異值能量和在原始信號各個頻率的奇異值能量和序列中排在第l位，則ωj對應的兩個奇異值是σ2l-1和σ2l。將式（2）中正交矩陣U用列向量表示為U=（u1，u2，…，um），ui為m×1 的列向量，正交矩陣V用列向量表示為V=（v1，v2，…，vn），vi為n×1 的列向量，則選擇奇異值σ2l-1和σ2l及矩陣U和V中對應的向量進行SVD 重構，可以得到：

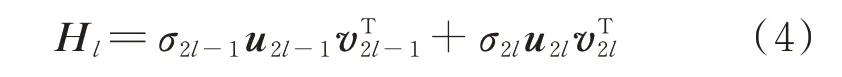
從矩陣Hl中恢復出信號，它就是原始信號x（i）中的頻率分量ωj。為了分離出多個頻率成分，只需按照這樣的方法選擇這些頻率對應的奇異值進行SVD 重構，就可從原信號中分離出它們。

因頻率幅值對奇異值的影響是最大的，在實際中選取奇異值可采用一種比較簡單的方法：一個頻率產生兩個非零奇異值［17］，而奇異值的大小主要是由頻率的幅值決定的，幅值最大的前I個頻率對應的奇異值一般是前2I個非零奇異值［18］。設原信號x（i）的頻率總數是J，并且含有噪聲，現需要從x（i）中分離出其中的I個頻率，為了說明問題方便，以幅值最大的前I個頻率的分離來說明。幅值最大的前I個頻率對應的是前2I個非零奇異值，因此可將原始信號x（i）構造的矩陣H的SVD 分解分為三個部分，寫成用列向量ui和vi表達的形式如下：

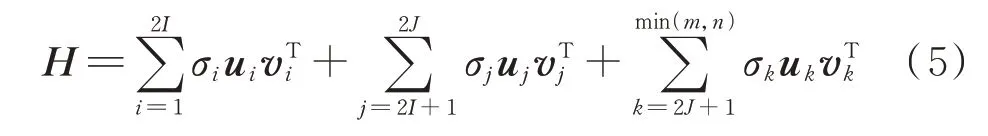
如果所需分離的I個頻率的幅值并不是幅值最大的那幾個，則只需利用式（3）計算每個頻率對應的奇異值能量和，根據所需分離頻率的奇異值能量和的大小順序，選擇相應的奇異值進行SVD 重構。通過這樣的奇異值選擇，得到重構矩陣共有2I個奇異值參與重構，從H1恢復的信號x1（i）就是所需分離的I個頻率。

對于柔性薄壁軸承振動信號中的正常周期性沖擊，從第2 節的分析可見它們的頻率是以2 倍轉頻為基頻的一系列倍頻，根據這些頻率的奇異值能量和的大小順序，選擇對應的奇異值進行SVD 重構，就可以從原始信號中分離出正常周期性沖擊，從而消除它們對故障周期性沖擊的影響。

4 故障沖擊特征的Morlet 小波提取

消除了正常周期性沖擊的干擾后，還必須進一步提取柔性薄壁軸承的故障周期性沖擊。這種故障周期性沖擊是快速衰減的調制沖擊，提取這種調制沖擊需要確定其調制頻帶，這是SVD 無法做到的。小波分析由于其良好的時頻局部化分解特性［19］，可以用來實現這一目的。這里采用Morlet 小波來提取柔性薄壁軸承的故障周期性沖擊，因為Morlet 小波的波形本身也是一個迅速衰減的調制沖擊，它和軸承以及齒輪的故障沖擊波形很相似，因而可以使故障沖擊在Morlet 小波基上獲得較大的投影，因此Morlet 小波很適合用來提取軸承和齒輪的故障周期性沖擊特征信息［20-22］。Morlet 小波的表達式為：

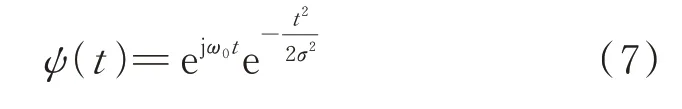
式中ω0為Morlet 小波的中心頻率，σ為高斯函數的窗寬參數。連續Morlet 小波變換是信號x（t）和Morlet 小波在連續尺度s下的伸縮函數的卷積：

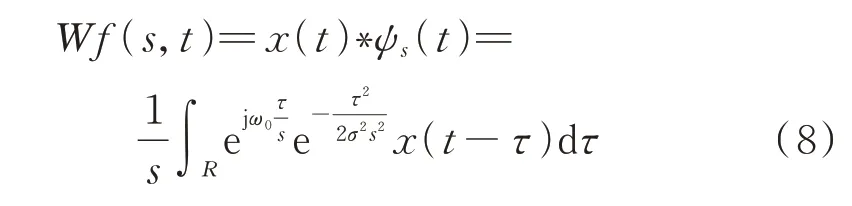
式（8）是模擬信號x（t）的連續Morlet 小波變換。對于采樣得到的柔性薄壁軸承振動的離散數字信號x（i），其連續Morlet 小波變換是x（i）和小波基ψs(i)的數字卷積，如下式所示：

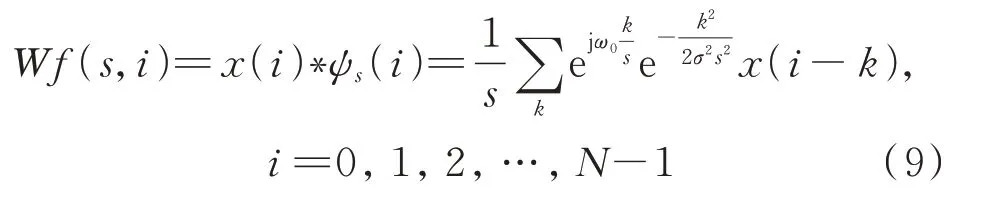
當尺度s連續變化時得到的一系列Wf（s，i）就是連續Morlet 小波變換的結果，尺度s和頻率f具有一一對應關系，如下式所示：

式中fs為對原始信號x（t）的采樣頻率。

Morlet 小波尺度對柔性薄壁軸承的故障沖擊特征提取結果有重要影響。不同尺度s下的Wf（s，i）反映了柔性薄壁軸承振動信號不同的細節特性，為了從一系列尺度下的Wf（s，i）中確定出含有柔性薄壁軸承故障沖擊特征的尺度，可以通過計算各尺度下Wf（s，i）的峭度來解決這問題。峭度是一個對沖擊信息比較敏感的參量，能夠反映信號中的沖擊特征［23-24］，如果某一個信號中含有沖擊，則這個信號的峭度值會比較大［25-26］，峭度在旋轉機械的故障診斷中有重要的應用。因此這里利用峭度來確定含有故障沖擊特征的小波尺度，對于柔性薄壁軸承振動信號的連續Morlet 小波變換結果，尺度s下的Wf（s，i）的峭度按下式計算：

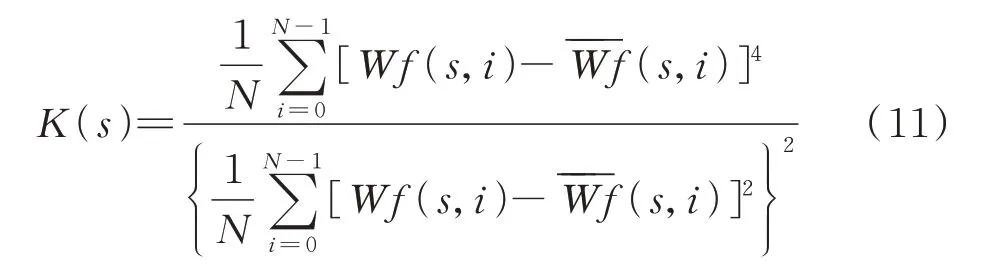
5 柔性薄壁軸承背景沖擊消除實例

5.1 正常周期性沖擊的SVD 分離

采用電火花加工對型號為SHF-32-120 的柔性薄壁軸承的外圈加工出一個深度和寬度都是1 mm的缺陷，如圖5所示。從圖5 可見柔性薄壁軸承的內外圈都非常薄，正是因為這種很薄的壁厚，使得這種軸承安裝在橢圓凸輪軸上后很容易變形成為橢圓軸承，其參數如表1所示。在圖2所示的振動測試系統上檢測這個外圈損傷的柔性薄壁軸承的振動，檢測時軸承轉速及其他檢測參數如表2所示。

圖5 外圈損傷的柔性薄壁軸承Fig.5 Flexible thin-wall bearing with injured outer ring

表2 外圈損傷柔性薄壁軸承振動檢測參數Tab.2 Vibration detection parameters of flexible thinwall bearing with damaged outer ring

檢測得到的振動信號如圖6所示。從圖6 中可看到信號中有強烈的周期性沖擊，但是這種沖擊并非缺陷產生的故障沖擊，而是橢圓長短軸產生的正常沖擊。從圖6 的頻譜可見這個沖擊是由以59.4 Hz 為基頻的一系列倍頻構成，59.4 Hz 正好是軸承轉頻29.7 Hz 的兩倍，根據第2 節對健康柔性薄壁軸承的振動分析可知，這種以二倍轉頻為基頻的周期性沖擊是橢圓長短軸旋轉產生的交替性沖擊，并非缺陷產生的故障沖擊。從圖6 可見，這種正常周期性沖擊很強烈，是柔性薄壁軸承振動的主要成分，缺陷產生的故障周期性沖擊完全被這種正常周期性沖擊掩蓋了。普通滾動軸承是沒有這種周期性沖擊的，這種沖擊是柔性薄壁軸承所特有的，它掩蓋了故障周期性沖擊，因此必須設法消除。

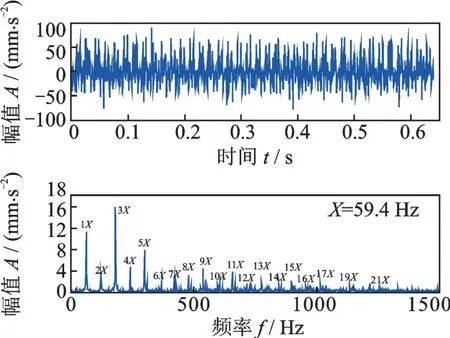
圖6 外圈損傷柔性薄壁軸承的振動信號及其頻譜Fig.6 Vibration signal of flexible thin-wall bearing with injured outer ring and its spectrum

現在用SVD 來分離這種正常周期性沖擊。圖6的原始信號長度是4096 點數據，因此利用原始信號構造一個2048×2049 的Hankel 矩陣并對其進行SVD 分解，得到正交矩陣U，V和奇異值對角矩陣D。從圖6 可見，正常周期性沖擊的頻率是以59.4 Hz 為基頻的一系列高次倍頻，圖6 的頻譜中標識出了這些頻率成分，它們分別是1～17 階頻率以及19和21 階頻率，一共有19 個頻率分量。這些頻率是頻譜中的主要頻率成分，它們的幅值在整個幅值譜中都是較大的。因為一個頻率產生兩個奇異值［17-18］，則19 個頻率分量對應38 個奇異值。根據式（3）所示頻率參數和奇異值大小的關系，選擇出相應的38 個奇異值進行SVD 重構，然后采用平均法［27］從重構矩陣中恢復出信號，結果如圖7所示。從圖7 的時域波形可見提取到非常明顯的周期性沖擊，其頻譜顯示提取到的信號就是由以59.4 Hz 為基頻的一系列倍頻組成的，分別是1～17 階頻率以及19 和21 階頻率，共19 個頻率分量，這和原始信號中正常周期性沖擊的頻率一致，而與故障周期性沖擊無關，這表明原始信號中的正常周期性沖擊成分被準確地分離出來了。還可以看到，分離出的周期性沖擊的頻譜中，兩兩相鄰的譜線之間沒有噪聲頻率存在，而且靠近沖擊各個倍頻的一些緊鄰的譜線也沒有混入進來，這是SVD 頻率提取的一個優點。對于常規的濾波器而言，它通過設定頻率范圍進行頻率提取，濾波器會把這個頻率范圍內的所有頻率都提取出來，但SVD 是通過選擇與每個頻率相對應的奇異值來實現頻率提取的，因此SVD 提取的頻率不會有其他頻率干擾。

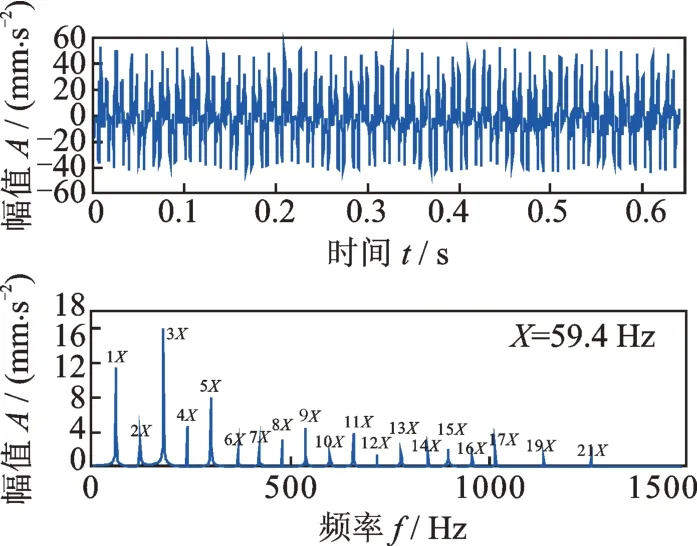
圖7 SVD 提取到的正常周期性沖擊背景信號及其頻譜Fig.7 Normal periodic impulse background signal extracted by SVD and its spectrum

根據式（6），只需從原始信號中簡單地減去所提取到的正常周期性沖擊背景信號，就可以消除正常周期性沖擊的干擾，這樣得到的結果如圖8所示。從圖8 的頻譜可見，在消除了正常的周期性沖擊干擾后，此時頻譜中已可觀察到外圈故障特征頻率307.8 Hz，但還是存在一些其他干擾頻率，為了得到更準確的故障周期性沖擊，還需要進一步提取故障沖擊。

圖8 消除了正常周期性沖擊干擾的柔性薄壁軸承振動信號及其頻譜Fig.8 Vibration signal of flexible thin-wall bearing in which the normal periodic impulses are eliminated and its spectrum

為了直觀地觀察正常周期性沖擊的消除效果，給出內圈旋轉一轉時周期性沖擊消除前后的振動信號對比（內圈旋轉一轉的時間是1/29.7 Hz=0.0337 s），如圖9所示，可見一個旋轉內由長軸引起的兩個沖擊和由短軸引起的兩個沖擊都已被針對性地消除了，沖擊消除效果非常好。

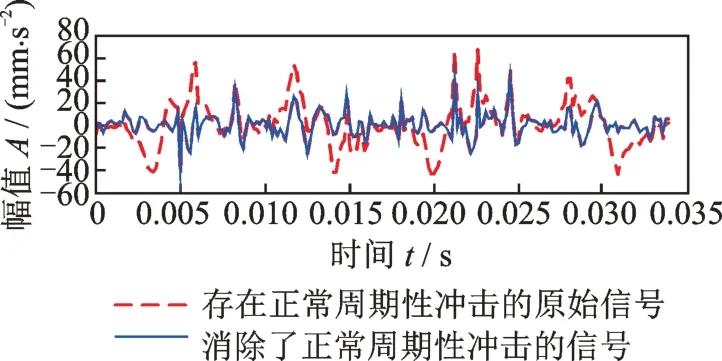
圖9 內圈旋轉一轉時正常周期性沖擊消除前后振動信號對比Fig.9 Comparison of vibration signals before and after the normal periodic impulses are eliminated when the inner ring rotates one revolution

也可以采用濾波器方法來分離這種正常周期性沖擊。從圖6 中的原始信號頻譜可見，正常周期性沖擊的諧波分量主要是1～21 階諧波，而第21 階諧波的頻率為21×59.4=1247.4 Hz，因此采用截止頻率為1248 Hz 的低通濾波器來分離這種周期性沖擊，結果如圖10所示，可見也分離出了正常周期性沖擊，但是和SVD 分離的正常周期性沖擊相比（圖7），濾波器分離出的正常周期性沖擊的各階諧波譜線之間還含有其他頻率成分，這當中包括故障特征頻率307.8 Hz，如圖10所示。因此濾波器方法分離出的周期性沖擊并不是純粹的正常周期性沖擊，部分故障特征信息也被分離出去了，故障特征信息有損失。而SVD 是利用頻率分量和奇異值的內在聯系點對點地將正常周期性沖擊的各階諧波分離出來，各階諧波的譜線之間沒有其他頻率成分，也不含有故障特征頻率（見圖7），是純粹的正常周期性沖擊。

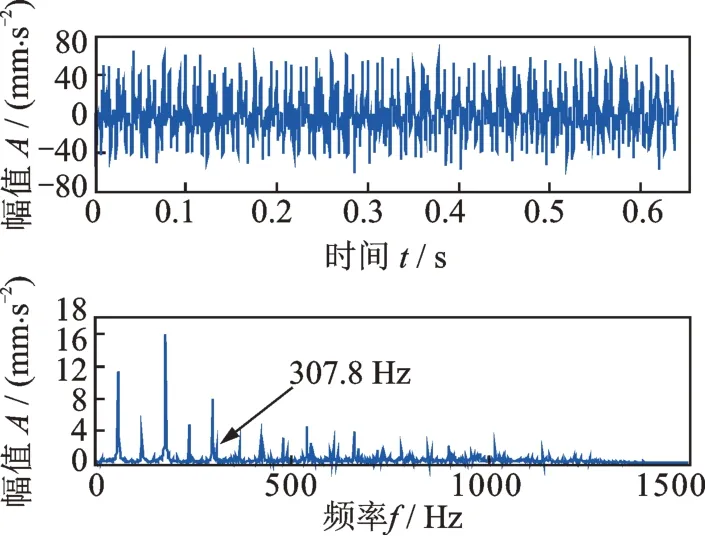
圖10 濾波器分離出的正常周期性沖擊背景信號及其頻譜Fig.10 Normal periodic impulse background signal extracted by the low pass filter and its spectrum

采用濾波器方法消除了正常周期性沖擊背景干擾后的振動信號如圖11所示，從其頻譜可見，前面一大頻段的信息都已經完全被濾波器消除了，而故障特征頻率307.8 Hz 卻并沒有在消除正常周期性沖擊后顯示出來。而利用SVD 方法消除正常周期性沖擊得到的結果中（圖8），只是準確地、點對點地消除了正常周期性沖擊的各階諧波頻率，并不影響其他頻率，其他頻率信息包括故障特征信息依然還保留在信號中，此時故障特征頻率307.8 Hz 已經顯示出來了（見圖8）。

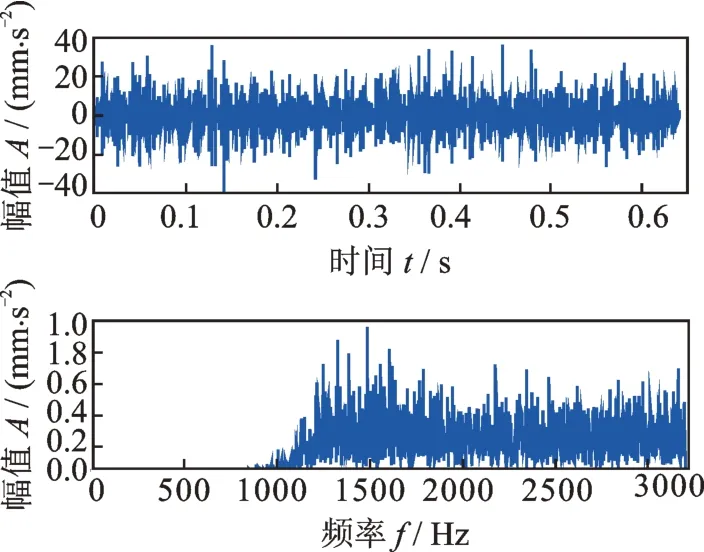
圖11 利用濾波器方法消除了正常周期性沖擊背景后的柔性薄壁軸承振動信號及其頻譜Fig.11 Vibration signal of flexible thin-wall bearing in which the normal periodic impulses are eliminated by the filter method and its spectrum

5.2 故障周期性沖擊特征的提取

利用連續Morlet 小波變換來提取柔性薄壁軸承的故障周期性沖擊特征，連續Morlet 小波變換的尺度數是1024 個。首先，對于沒有消除正常周期性沖擊的原始振動信號、其連續Morlet 小波變換結果如圖12所示，計算各個尺度的峭度，結果如圖13所示，可見最大峭度位于第969 個尺度，峭度值為11.47，這個尺度的Morlet 小波變換結果如圖14所示，其包絡譜顯示，外圈故障特征頻率307.8 Hz 雖然被提取出來了，但是故障特征頻率的高倍頻并不明顯，只有二倍頻相對明顯，并且故障特征頻率基頻及其二倍頻周圍還存在較多的頻率干擾，如圖14 中紅色圈內所示，這些頻率是正常周期性沖擊產生的干擾頻率。

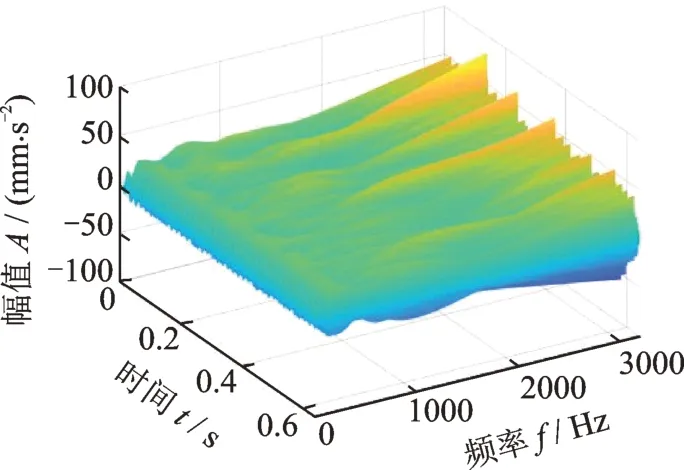
圖12 原始振動信號的連續Morlet 小波變換結果Fig.12 Continuous Morlet wavelet transform result of the original vibration signal

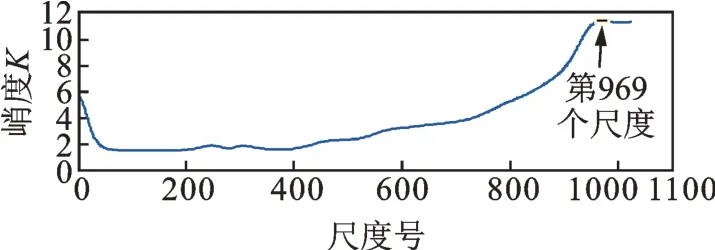
圖13 原始振動信號的連續Morlet 小波變換各個尺度的峭度Fig.13 Kurtosis of continuous Morlet wavelet transform results of original vibration signal at various scales

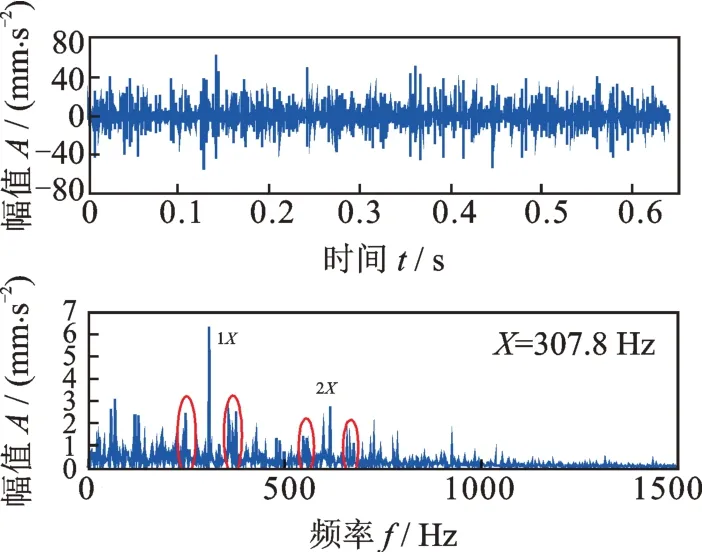
圖14 未消除正常周期性沖擊時提取到的故障特征Fig.14 Fault feature extracted when the normal periodic impulses are not eliminated

而對于消除了正常周期性沖擊的振動信號，其連續Morlet 小波變換結果如圖15所示，可見它和圖12 的連續Morlet 小波變換結果存在明顯區別。這種變換結果的各個尺度的峭度如圖16所示，其中最大峭度位于第971 個尺度，其峭度值為11.32，這低于未消除正常周期性沖擊時的最大峭度值11.47，分析其原因，是因為正常周期性沖擊也會對峭度值產生貢獻，當正常周期性沖擊消除后，振動信號的峭度值就減小了。消除正常沖擊后最大峭度值所在尺度的Morlet 小波變換結果如圖17所示。

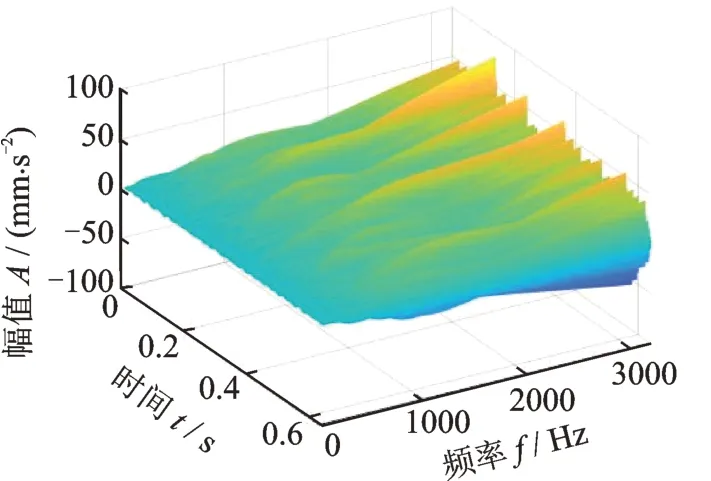
圖15 消除正常周期性沖擊后的連續Morlet 小波變換結果Fig.15 Continuous Morlet wavelet transform result after the normal periodic impulses are eliminated

圖16 消除正常周期性沖擊后的連續Morlet 小波變換各尺度的峭度Fig.16 Kurtosis of continuous Morlet wavelet transform result at various scales after the normal periodic impulses are eliminated

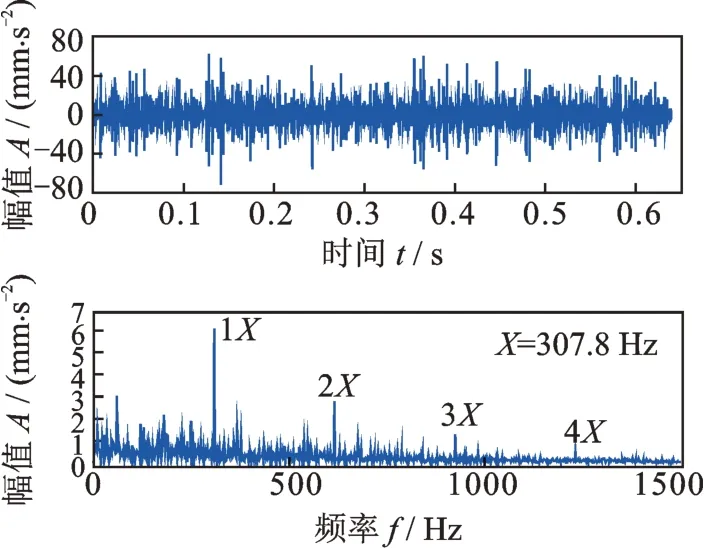
圖17 消除正常周期性沖擊后的故障特征提取結果Fig.17 Fault feature extraction result after the normal periodic impulses are eliminated

和沒有消除正常周期性沖擊的包絡譜相比（圖14），可見圖17 的包絡譜中故障特征頻率更加突出，故障特征頻率307.8 Hz 時的2，3 和4 階高倍頻非常明顯，并且故障特征頻率及其倍頻周圍的干擾頻率更少，而圖14（b）中只有基頻及2 倍頻，其周圍的干擾頻率也較多。無論是正常周期性沖擊還是故障周期性沖擊，其在頻域都是由基頻和一系列倍頻構成，倍頻多，說明周期性沖擊提取效果好。這可從正常周期性沖擊的結果來說明（圖7），它是很強烈的周期性沖擊，其在頻域內，基頻及其倍頻達到19 個（參見圖7）。對于消除了正常周期性沖擊的故障周期性沖擊提取結果，其特征頻率及其倍頻比沒有消除正常周期性沖擊的特征頻率及其倍頻多。這種結果表明，在消除了正常周期性沖擊的干擾后，柔性薄壁軸承的故障沖擊特征被更加突出地顯示出來了。

定義故障特征頻率能量比率作為特征提取的定量評價指標，設所提取到的故障周期性沖擊的包絡譜用es（i）表示，i=0，1，2，…，int（N/2），N為原始信號長度，int（x）表示對x取整，不四舍五入，取int（N/2）是表示取包絡譜的正頻率部分即可，因為頻譜是對稱的。設包絡譜中第k階故障特征頻率的幅值用ak表示，則故障特征頻率的能量比率定義如下：

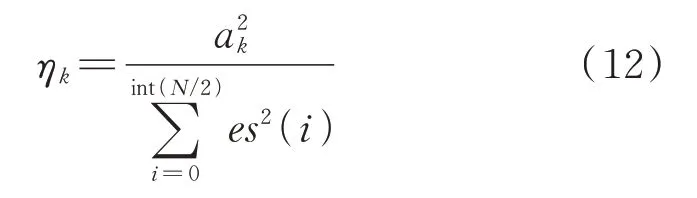
這個參數反映了所提取的故障特征頻率的能量占總頻譜能量的比例。對于消除了正常周期性沖擊和未消除正常周期性沖擊的振動信號，所提取的故障特征頻率的能量比率如表3所示。可以看到消除正常周期性沖擊后，故障特征頻率的能量比率明顯提高。

表3 故障特征頻率的能量比率對比Tab.3 Comparison of energy ratio of fault feature frequency

6 結論

（1）柔性薄壁軸承的內外圈是橢圓，在軸承旋轉時橢圓的長短軸會對軸承造成周期性沖擊。內圈旋轉一圈，長軸產生兩個沖擊，短軸也產生兩個沖擊，長、短軸產生的沖擊方向相反，其頻率都是轉頻的兩倍。這種正常的周期性沖擊掩蓋了軸承元件缺陷引起的故障周期性沖擊，使得柔性薄壁軸承的故障沖擊特征不明顯。

（2）正常周期性沖擊的頻率是柔性薄壁軸承振動的主要頻率成分，利用奇異值和頻率的內在聯系，采用SVD 來分離柔性薄壁軸承的正常周期性沖擊，選擇正常周期性沖擊的頻率成分所對應的奇異值進行SVD 重構，就可從原始振動信號中分離出正常周期性沖擊，實例結果表明SVD 分離出的正常周期性沖擊波形清晰，無其他頻率干擾。

（3）利用連續Morlet 小波變換對消除了正常周期性沖擊的柔性薄壁軸承振動信號進行故障特征提取，并選擇最大峭度對應的尺度為最佳特征尺度，實例分析結果表明，消除正常沖擊后提取到的故障沖擊特征頻率更加清晰，其高倍頻非常明顯，干擾頻率少，優于沒有消除正常周期性沖擊情況下的故障特征提取效果。