交互偏移支持矩陣機及其在滾動軸承故障診斷中的應用

徐海鋒，潘海洋，鄭近德，童靳于

（安徽工業大學機械工程學院，安徽馬鞍山 243002）

引言

滾動軸承作為機械設備中的一類重要零部件，其工作時往往處于高速旋轉的運行狀態，長時間工作會致使滾動軸承等部件出現一定的疲勞損傷。因此，如何對滾動軸承的健康狀況進行智能監測和診斷，已成為眾多學者研究的熱點內容與方向。

隨著人工智能的發展，基于模式識別的滾動軸承智能故障診斷方法得到了廣泛的研究和應用，如人 工 神 經 網 絡（Artificial Neural Networks，ANN）［1］、K-最近鄰（K-nearest Neighbor，KNN）［2］和支持向量機（Support Vector Machine，SVM）［3］等。上述方法通過不斷完善，已被應用于故障診斷、文本分類、圖像識別等領域。SVM 作為其中最穩定的一種分類方法，擁有良好的泛化能力和稀疏性。在解決二分類問題時，傳統的SVM 通過將原始數據映射到一定維度特征空間，構造兩個平行超平面來分割不同類型樣本。當原始數據線性不可分時，如異或（Exclusive OR，XOR）問題，SVM 很難找到一對線性超平面對數據樣本進行有效分割。針對該類問題，Li 等［4］提出多目標近似支持向量機（Multi-task Proximal Support Vector Machine，MPSVM），其通過求解兩個廣義特征值問題，構造出兩個非平行的分類面對不同數據進行分割，能夠較好應對異或問題；Chen 等［5］以經驗風險最小化作為基本框架提出了孿生支持向量機（Twin Support Vector Machine，TWSVM），其將SVM 的優化問題轉變為求解兩個較小的線性規劃問題，構造一對非平行的分類面，實現了分類效率的提升。為提高TWSVM 算法的泛化能力，Wang 等［6］在構造目標函數的過程中引入正則項，提出孿生有界支持向量機（Twin Bounded Support Vector Machine，TBSVM），其使用連續過度松弛技術（Successive Over-Relaxation，SOR）［7］和正則項解決模型凸優化和魯棒性問題。

上述方法本質上都是基于向量進行建模和分類，當處理微弱故障信號的診斷問題時，僅提取若干故障可能無法完成故障的有效識別。為了解決該問題，Luo 等［8］受核范數的啟發提出支持矩陣機（Support Matrix Machine，SMM），以矩陣樣本作為直接輸入，充分挖掘了矩陣行列間的結構信息，這為后續研究提供了新的思路，如魯棒支持矩陣機（Robust Support Matrix Machine，RSMM）［9］、稀疏支持矩陣機（Sparse Support Matrix Machine，SSMM）［10］、多分類支持矩陣機（Multiclass Support Matrix Machine，MSMM）［11］等。但這類矩陣分類器通常是線性的，無法解決矩陣數據線性不可分的問題，同時，還存在訓練誤差大、過擬合等不足。鑒于此，Gao等［12］基于矩陣數據構造非平行分類器的思想，利用左右奇異值向量構造目標函數提出了一種孿生多秩支持矩陣機（Twin Multiple Rank Support Matrix Machine，TMRSMM）；Jiang 等［13］利用多秩左右投影矩陣替換左右投影向量來構造目標函數，提出了多秩多線性孿生支持矩陣機（Multiple Rank Multi-Linear Twin Support Matrix Machine，MRMLTSMM）。TMRSMM 和MRMLTSMM 利用左右投影思想解決了非線性矩陣數據的分類問題，且作為非平行超平面分類器（Nonparallel Hyperplane Classifier，NHC）的一類方法，它們在構造分類超平面時，遵循“尋找一對非平行的超平面，使得每一類樣本聚集在相應超平面的附近，同時，另一類樣本盡可能地遠離該平面”的思想，提高了模型的分類精度。但是，當數據樣本存在XOR 問題時，僅依靠非平行超平面和難以完成復雜數據的有效分割。

基于上述研究，考慮矩陣擁有保持數據結構信息完整的優勢以及提高模型泛化能力的問題，本文提出一種新的矩陣數據分類方法——交互偏移支持矩陣機（Interactive Deviation Support Matrix Machine，IDSMM）。IDSMM 以矩陣作為輸入與建模元素，通過構造一對交互超平面將兩類復雜樣本分割開來，使得正類樣本靠近超平面b1=1，負類樣本盡可能遠離此平面。同時，引入多秩左右投影矩陣構造目標函數，使IDSMM 具有更好 的 數 據 擬 合 能 力 。 與 TMRSMM 和MRMLTSMM 方法相比，IDSMM 構造兩個交互偏移超平面和，從幾何學上看，兩平面間的“間隔”將變大，每一個超平面距離異類樣本更遠，提高了模型的泛化能力。最后，為了驗證所提方法的性能，采用兩種不同的滾動軸承故障數據集進行驗證，實驗結果表明，與其他分類器相比，IDSMM 在滾動軸承故障診斷中具有更優異的分類性能。

1 交互偏移支持矩陣機原理

1.1 支持矩陣機

支持矩陣機是一種基于經驗風險最小化的矩陣分類器，其利用鉸鏈損失和正則項組合解決一個凸優化問題。同時，SMM 的核心思想是尋找兩個平行超平面，將正負兩類樣本分割開來。為了得到兩個超平面，構造目標函數如下式所示：

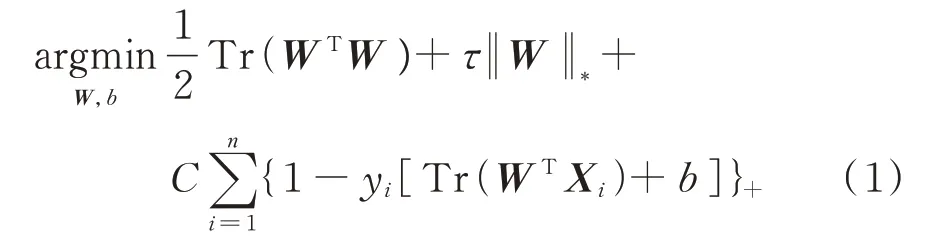
式中W∈Rm×m為權重矩陣，{Xi∣i=1，…，n}∈Rm×n為矩陣樣本，yi=(-1，1)為對應類別標簽，b為偏移量，為正則項，τ為正則項系數，為鉸鏈損失函數，C為損失參數。

利用交替方向乘子法ADMM 可以解決目標函數（1）的求解問題，得到權重矩陣W和偏移量b。然后構建如下決策函數，對于新的未知樣本，有：

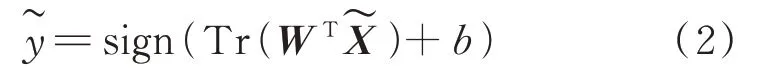
SMM 是一種可以充分利用輸入矩陣樣本結構特征的分類器，其核心思想還是尋找兩個平行的分類面，面對一些復雜數據時，很難有效地找到兩個平行分類超平面去劃分兩類樣本。

1.2 交互偏移支持矩陣機

SMM 方法的核心在于尋找一個最優分類面Tr(WTX)+b=0 對不同數據進行劃分，根據VC間隔理論，在距離超平面處，分別存在上下邊界Tr(WTX)+b=1 和Tr(WTX)+b=-1，兩個邊界間的距離稱為最大間隔。由于這種平行超平面的構造形式，使得SMM 無法有效處理一些復雜數據。為了解決這個問題，IDSMM 采用一對交互偏移超平面，同時，不同于以往NHC 方法的超平面構造形式，IDSMM 擬將交互偏移超平面構造為和為了實現這個目標，盡可能使目標函數中的和最小。這兩項在目標函數中表示每一類樣本與相應超平面的平方距離的和。通過最小化這兩項，使得正類樣本盡可能地接近并遠離，同時，負類樣本盡可能的接近并遠離b1=1。IDSMM 方法的詳細步驟如下：

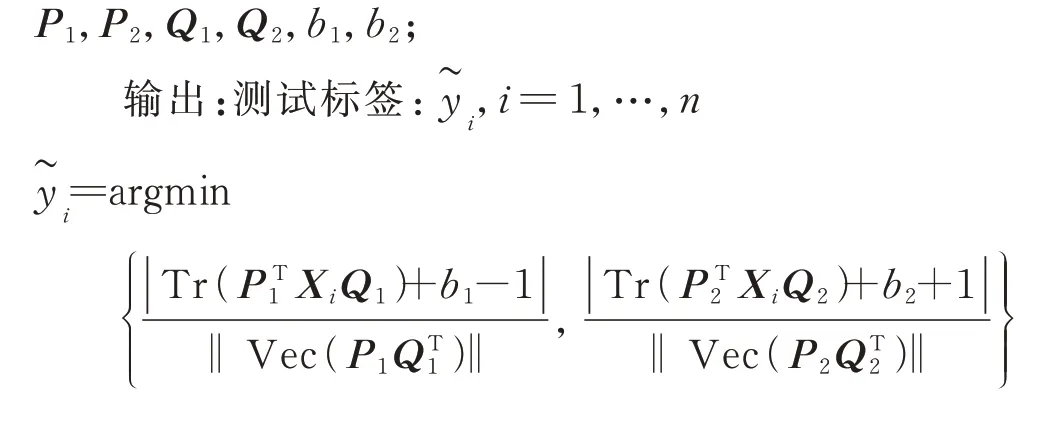
2 實驗分析

為了驗證本文提出的IDSMM 的分類性能，本節分別使用安徽工業大學滾動軸承故障振動信號數據集和湖南大學錐齒輪-滾動軸承故障振動信號數據集對其進行測試和分析，采用Accuracy，Recall，Precision，F1-score 和Kappa 作為模型評價指標。Accuracy 為正確率，是最常用的分類性能衡量指標，表示所有測試樣本中分類器能正確分類的占比；Recall 表示召回率，指在實際的測試樣本中，被分類器正確識別出來的正類樣本占比；Precision 表示精確率，指測試的正類樣本中，真正能被模型識別出來的屬于正類的樣本占比；F1-score 為精確率和召回率的調和值；Kappa 系數常用于一致性檢驗，用于判斷模型的分類精度。以上五種指標在一定范圍內，值越大，表示模型的分類性能越好。

同時，為了驗證所提方法的優越性，選擇SMM，SSMM，RSMM 和MRMLTSMM 作為對比（所有實驗均在Intel（R）Core（TM）i5（2.20 GHz），RAM 8 GB 計算機上的Matlab2019b 運行）。由于SMM，RSMM，SSMM，MRMLTSMM 和IDSMM 等方法的輸入元素為矩陣，需要構造輸入矩陣來完成分類和建模。辛幾何相似變換方法［15］作為一種新的信號降噪與分析方法，已被證明具有良好的特征提取能力，因此，本文擬采用辛幾何相似變換分析原始信號，以獲得可以保存完整結構信息的辛幾何系數矩陣。

IDSMM 的分類流程結構如圖1所示：1）將不同狀態的數據作為訓練集，通過辛幾何相空間重構后輸入到主程序，得到決策函數（30）；2）將不同狀態的數據作為測試集輸入到決策函數（30）；3）對不同的模型采取同樣的方法完成測試，并進行對比分析。

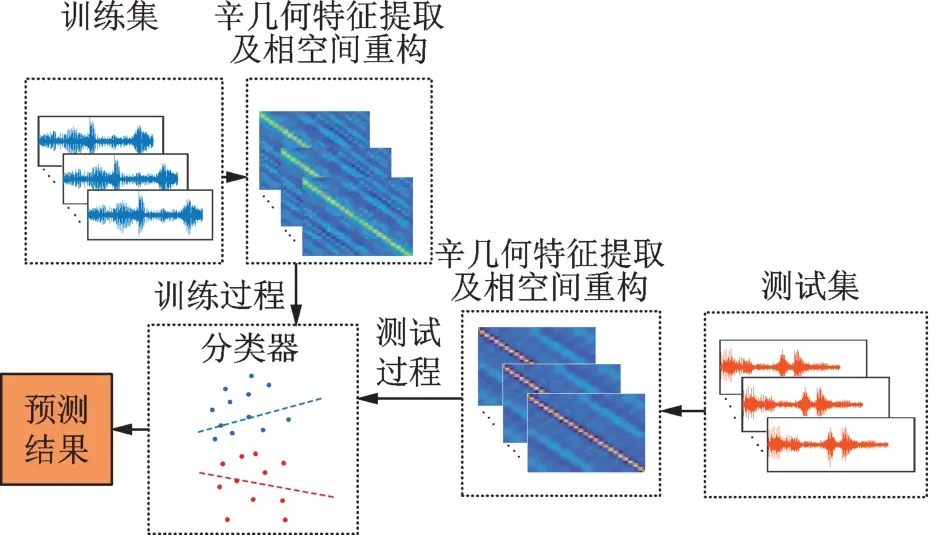
圖1 分類流程圖Fig.1 Classification flow chart

2.1 實驗1

為了驗證本文所提方法的分類性能，選擇安徽工業大學滾動軸承故障振動信號數據集進行分類測試。滾動軸承故障模擬試驗臺如圖2所示。試驗所用軸承型號為SKF 6205 深溝球軸承，使用電火花加工技術分別在軸承上布置出內圈故障、外圈故障和滾動體故障。試驗過程中，設置負載為5 kN，主軸轉速為900 r/min，采樣頻率為10240 Hz。同時，利用加速度傳感器分別采集滾動軸承在正常狀態、內圈故障狀態、外圈故障狀態及滾動體故障狀態下的加速度信號，詳細試驗滾動軸承狀態和試驗參數見表1（實驗選擇260 組訓練和測試樣本）。

圖2 滾動軸承故障模擬試驗臺Fig.2 Roller bearing fault simulation test bench

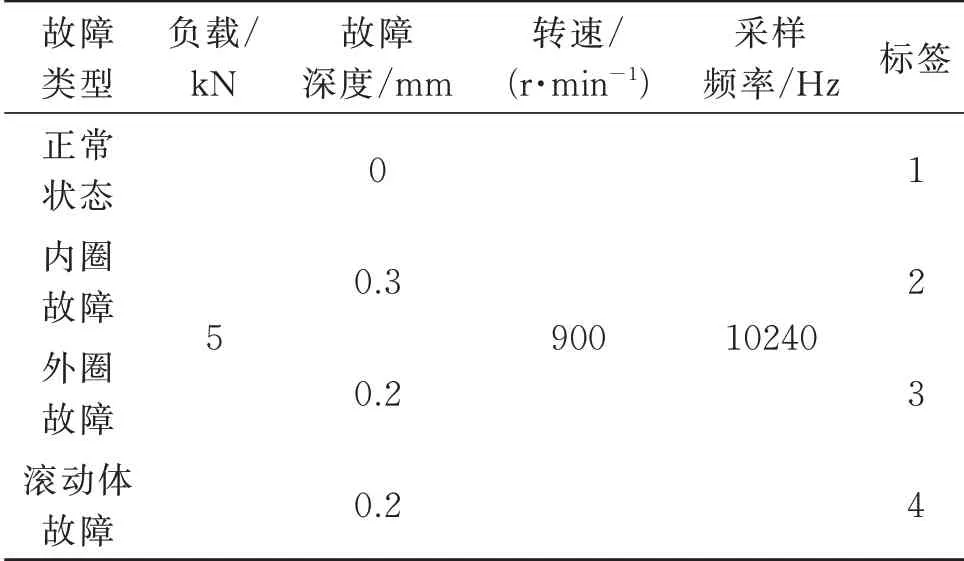
表1 滾動軸承試驗參數Tab.1 Experimental parameters of rolling bearings

IDSMM 的性能與參數K，C1，C2，C3和C4相關，因此需要在訓練前選擇最優值。首先，根據文獻［6，13］相關取值方法，通過實驗取C1=0.1，C2=0.1，C3=0.01 和C4=0.01。此外，對于參數K，設置K的取值范圍為1～10，選取180 組訓練和測試樣本并采用5 折交叉驗證進行實驗。圖3 為IDSMM 在K為1～10 范圍內得到的五種指標對比，表2 為訓練時間。

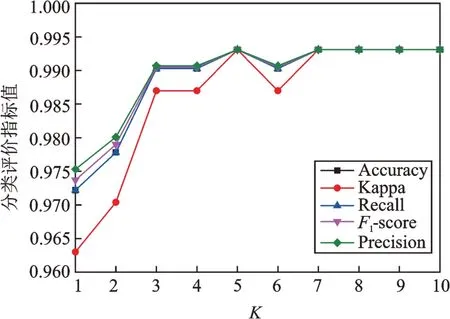
圖3 不同K 的IDSMM 五種指標對比Fig.3 Comparison of five indicators of IDSMM in different K

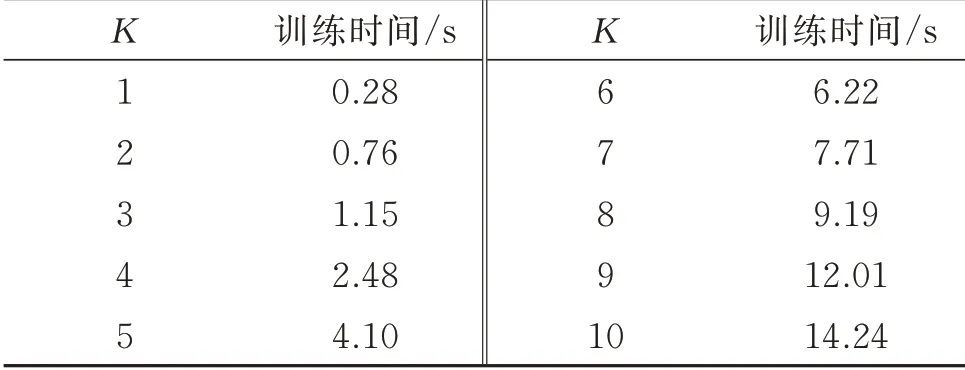
表2 不同K 的IDSMM 訓練時間Tab.2 IDSMM training time in different K

從圖3 中可以看出，IDSMM 分類器在不同的K下均能夠保持較高的準確率。總體上，隨著K的增大，各個指標逐漸增大，最終保持平穩狀態，且K=5或K≥6 時分類準確率最高。IDSMM 采用交替迭代求解左右投影矩陣，隨著K值的增大，P1，P2，Q1和Q2的矩陣尺寸增大，模型計算的復雜度增大，從而使得耗時越來越長。因此，為了使IDSMM 分類性能達到最佳的同時縮短訓練時間，選擇K=5 作為模型的輸入參數，此時五種指標均處于較高水平，訓練用時相對較短。

IDSMM 采用SOR 方法求解對偶問題，通過交替迭代求解最優P1，P2，Q1和Q2。圖4 展示了該模型在訓練過程中交替求解P1，P2，Q1和Q2的收斂過程曲線。由于P1，Q1和P2，Q2分別求解，所以會有兩條不同的收斂曲線，其中，P1和Q1表示求解P1和Q1過程中目標函數（5）的收斂曲線，P2和Q2表示求解P2和Q2過程中目標函數（6）的收斂曲線。從圖4 可以看出，IDSMM 經過較少的迭代次數可以快速達到收斂狀態。

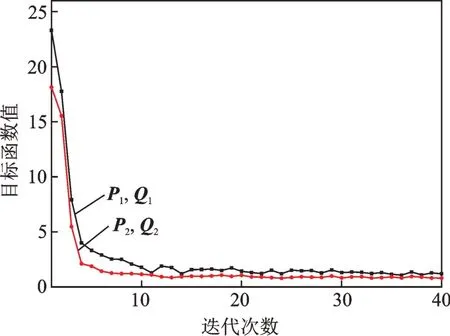
圖4 IDSMM 收斂曲線Fig.4 IDSMM convergence curve

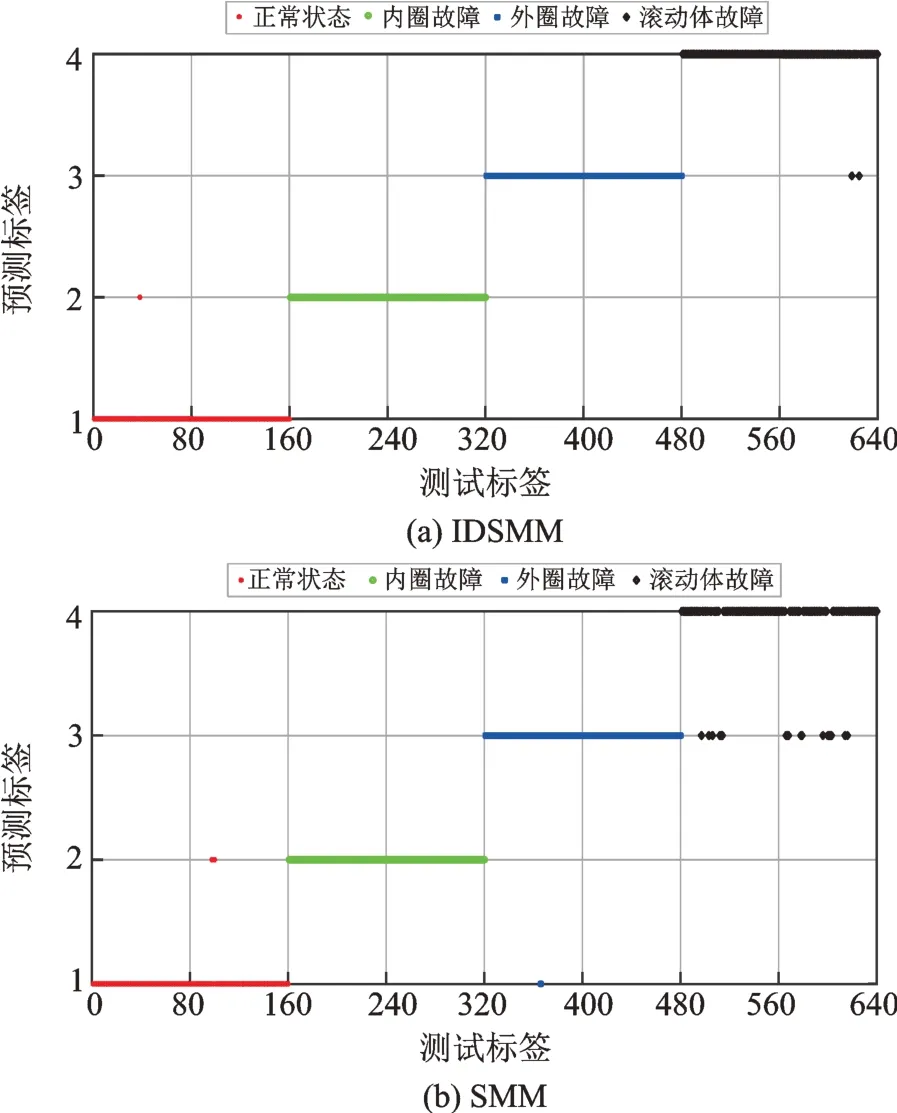
SMM，RSMM，SSMM 和MRMLTSMM 模型中均具有不同的參數，為了保障測試的客觀性，采用5 折交叉選擇各個參數，五種分類器的最終參數選擇如表3所示。然后，分別使用IDSMM，SMM，RSMM，SSMM 和MRMLTSMM 對100 個樣本進行訓練，得到五種預測模型，再用160 個樣本進行測試，識別結果如圖5所示，從圖中可以看出，IDSMM將第1 類和第4 類的樣本錯分，其他類別全部被正確分類。SMM，RSMM 和SSMM 存在較多第4 類錯分給第3 類的樣本，MRMLTSMM 方法錯分率較低。表4 為五種分類器的五種指標對比，從表中可以看出，IDSMM 五個指標均最高，表示IDSMM 模型有著最好的分類性能。

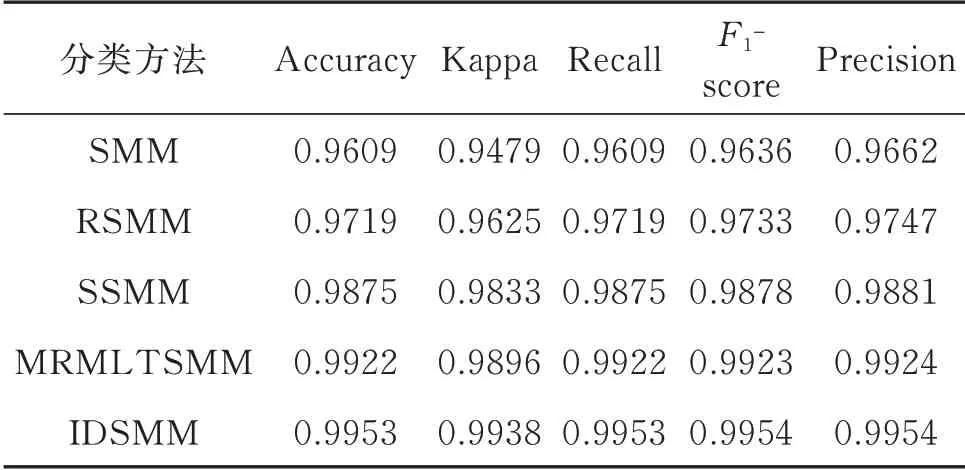
表4 五種方法的分類性能對比Tab.4 Comparison of classification performance of five methods

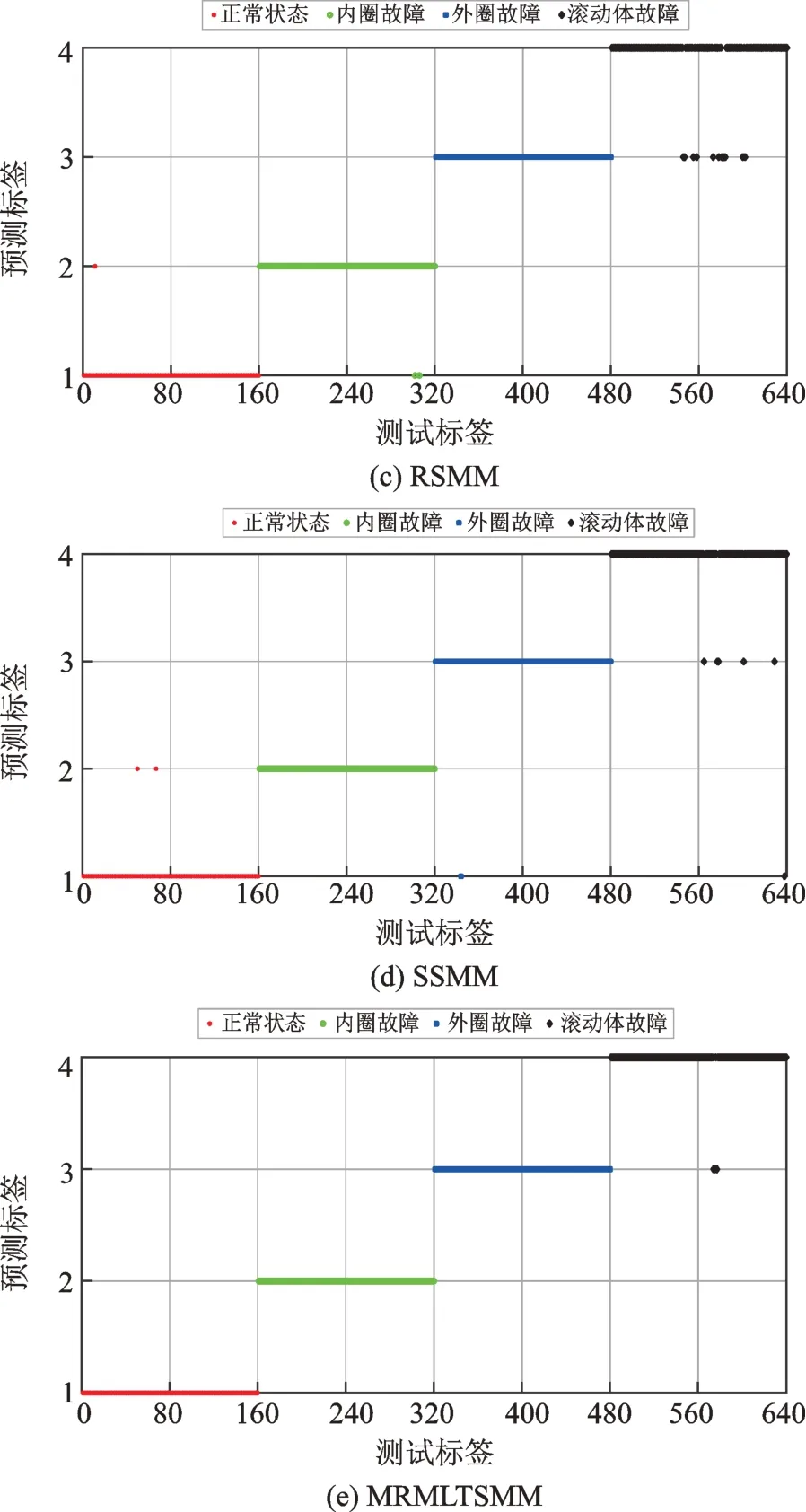
圖5 五種方法分類結果Fig.5 Classification results of five methods

表3 五種方法的參數Tab.3 Parameters of five methods

為避免偶然因素的發生，得到更好的測試結果，選擇260 個樣本采用5 折交叉驗證方法再次進行測試。圖6 展示了五種分類器分別在5 折交叉驗證下得到的結果（1～5表示每次的分類準確率）。從圖6中可以看出，IDSMM 分類性能最好，平均分類正確率達到99.62%，SMM，RSMM，SSMM 和MRMLTSMM的平均分類正確率分別為96.25%，97.89%，98.56%和99.04%。IDSMM 方法在構造分類面時，其為不同的樣本分別構造對應的分類面，得到一對交互偏移分類超平面，能夠更有效地處理復雜數據，同時，IDSMM 采用左右投影矩陣方法，降低了過擬合的影響。其次，相比MRMLTSMM，IDSMM 的分類面間的間隔增大，從而使分類性能提高。SSMM 方法同樣采用構造一對交互超平面進行分類，同時其模型本身具有稀疏屬性，也實現了較為出色的分類性能。盡管RSMM 在建構模型時提高了魯棒性，但在此復雜數據下未表現出良好的分類性能。SMM是一種基于經驗風險最小化的分類器，其使用常規的方法來構造兩個平行的分類超平面，模型的泛化能力較差，因此分類結果不佳。

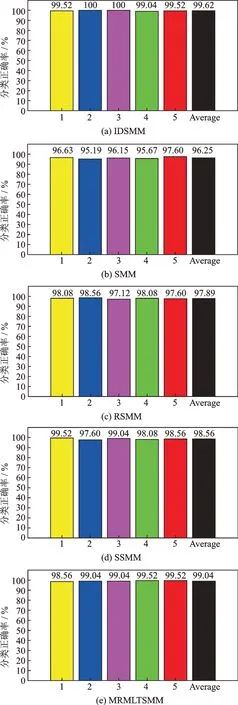
圖6 5 折交叉驗證下五種方法的結果Fig.6 Results of five methods in 5-CV

綜上所述，IDSMM 分類方法具有良好的分類性能，其模型參數在一定范圍內，對整體模型的影響有限。同時，實驗驗證了其收斂的有效性，在較短的時間內，該方法能夠得到最優解并完成訓練和測試。

2.2 實驗2

IDSMM 在安徽工業大學滾動軸承故障振動信號數據集上展示了良好的分類性能，為了進一步驗證論文提出方法的性能，選擇湖南大學錐齒輪-滾動軸承故障振動信號數據集再次進行分類測試。試驗采用的軸承為型號SKF 6206。試驗過程中，設置載荷為4 kN，電機轉速為900 r/min，采樣頻率為8192 Hz。軸承故障信息和試驗參數如表5所示（選擇350 組訓練和測試樣本）。

表5 滾動軸承試驗參數Tab.5 Experimental parameters of rolling bearings

圖7 展示了IDSMM 方法在K為1～10 范圍內選擇180 組訓練和測試樣本進行實驗得到的五種指標對比，表6 為訓練時間。從圖7 中可以看出，當K=4，模型分類正確率達到100%。隨著K增大，IDSMM 分類性能明顯提升，K≥3 以后，分類準確率、召回率、F1-score 和Kappa 均處于較高水平。說明該模型在K≥4 的情況下能達到最佳的分類性能，但K值越大，訓練用時越久。基于以上分析，選擇K=4 作為模型的輸入參數。

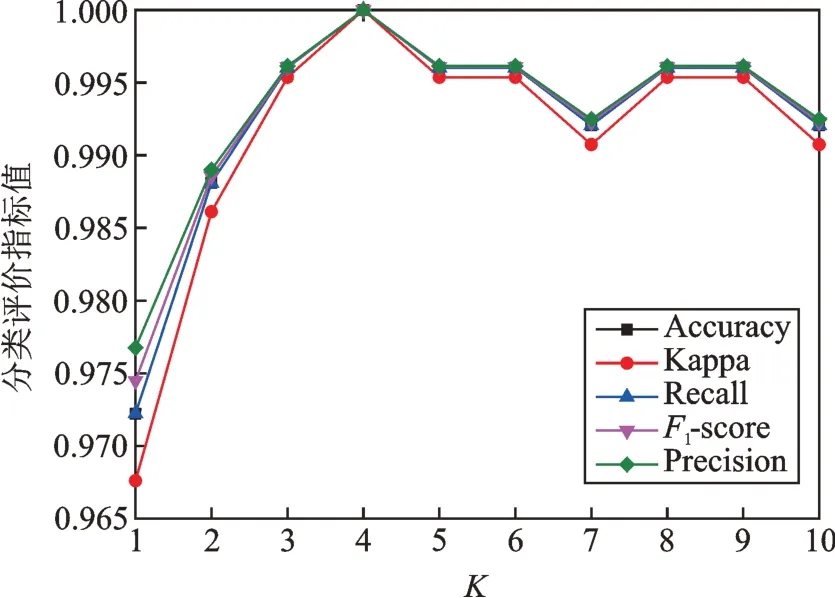
圖7 不同K 的IDSMM 的五種指標對比Fig.7 Comparison of five indicators of IDSMM in different K

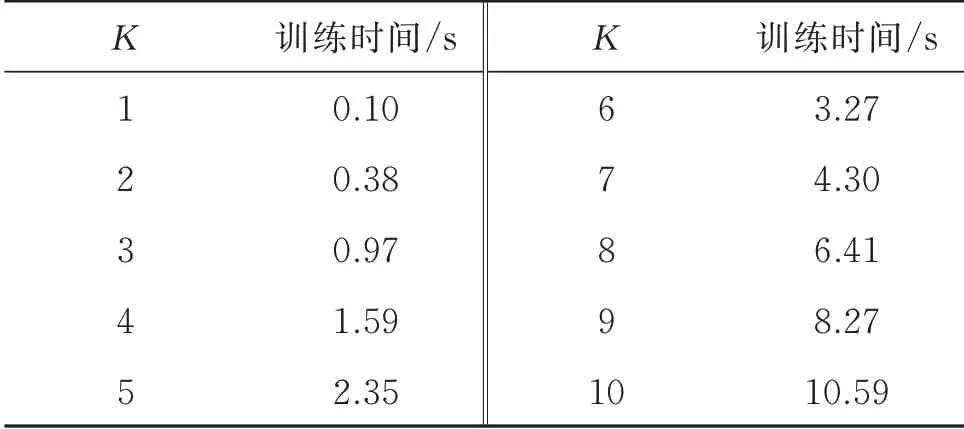
表6 不同K 的IDSMM 訓練時間Tab.6 IDSMM training time in different K

選擇150 組樣本作為訓練集，剩余200 組作為測試集，分別使用五種方法進行實驗，實驗結果如表7、圖8 和9所示。從表7 和圖8 中可以看出，IDSMM 五種指標均高于SMM，RSMM，SSMM 和MRMLTSMM，再次證明了該方法有著良好的分類性能。圖9 為根據分類結果得到的混淆矩陣。從圖中可以清楚看出，在增加故障類別，提高數據復雜度后，IDSMM 存在較少的錯分現象，但第1 類和第5類仍被全部正確區分。考慮到偶然因素的存在，再次選擇350 組樣本進行5 折交叉驗證測試，圖10 展示了五種方法在5 折交叉驗證下的測試結果。從圖中可以看出，IDSMM 方法具有較高的分類正確率，平均正確率可以達到99.80%，SMM，RSMM，SSMM 和MRMLTSMM 的平均分類正確率分別為97.43%，98.53%，99.14%和99.63%。相比其他四種方法，IDSMM 方法在5 次分類中的正確率均穩定在99%以上，識別效果最佳。究其原因在于，SMM利用輸入的特征樣本構建目標函數，特征數的增加對其模型的影響較大，使得分類準確率波動較大。SSMM 和RSMM 通過增加稀疏屬性和約束使得模型具有魯棒性以及冗余特征的抗干擾能力，但是，SSMM 和RSMM 本質上還是構造平行超平面，對復雜數據難以完成有效的樣本分割。

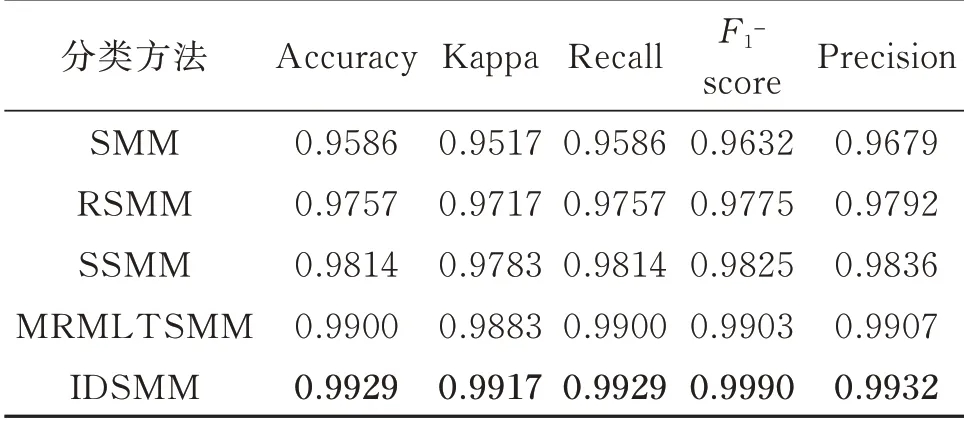
表7 五種方法的分類性能對比Tab.7 Comparison of classification performance of five methods

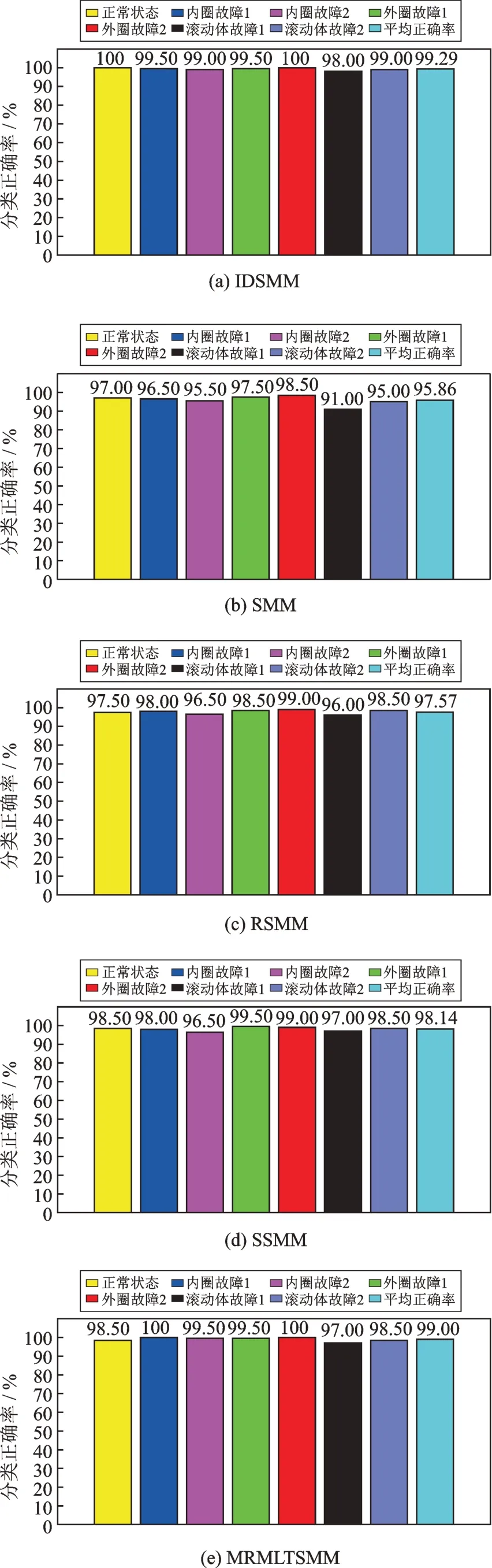
圖8 五種方法的分類結果Fig.8 Classification results of the five methods

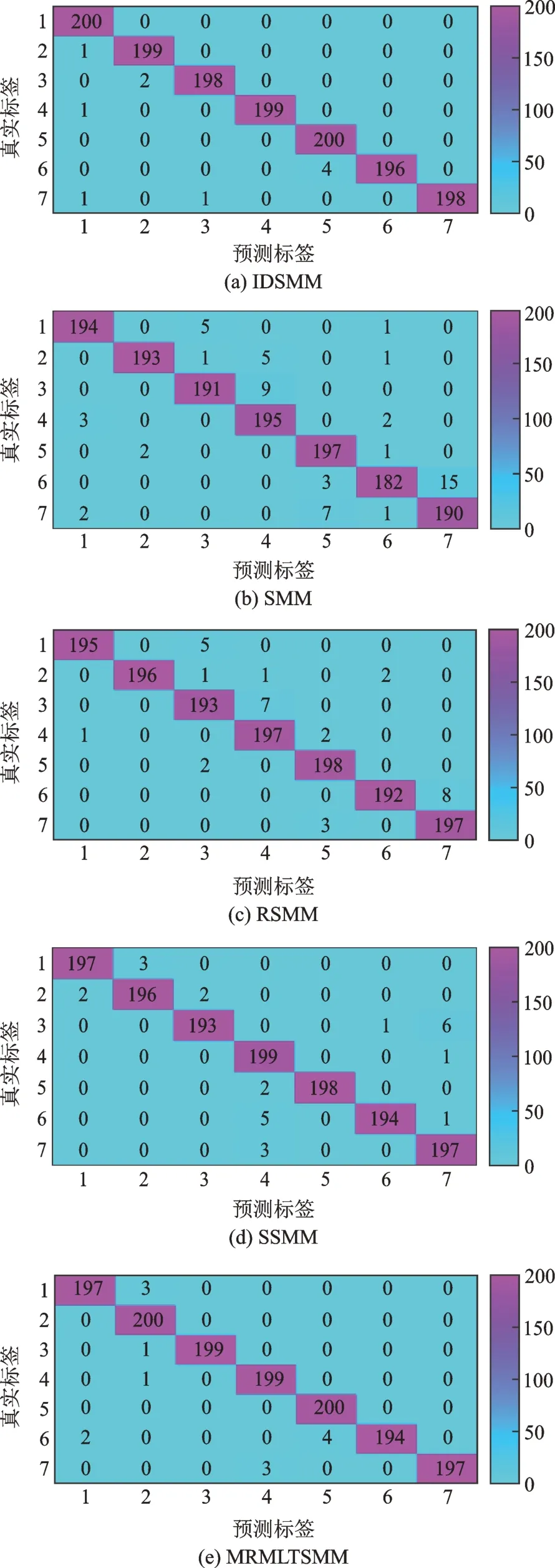
圖9 五種方法的混淆矩陣Fig.9 Confusion matrix of five methods

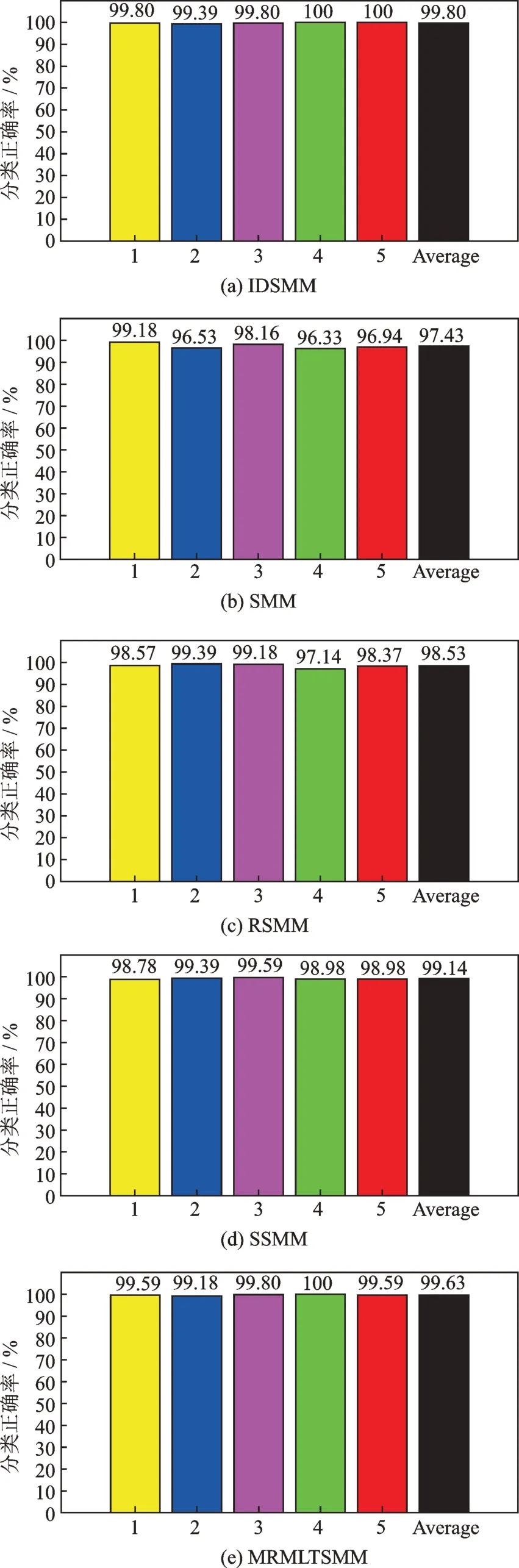
圖10 5 折交叉驗證五種方法的結果Fig.10 Results of five methods in 5-CV

為了判斷IDSMM 方法的小樣本分析能力，隨機抽取10，20，30，40，50，60，70，80，90，100 個樣本作為訓練樣本，150 個測試樣本。IDSMM，SMM，RSMM，SSMM 和MRMLTSMM 五種方法得分類結果如圖11所示。從圖11 中可以看出，IDSMM 和MRMLTSMM 方法都具有優異的小樣本數據分析能力，當訓練樣本數為10～40 時，IDSMM 分類正確率比MRMLTSMM 略高。總的來說，無論訓練樣本數多少，IDSMM 和MRMLTSMM 分類準確率都高于其他三種方法。SSMM 和RSMM 的識別性能低于IDSMM，但也表現出了良好的小樣本分析能力。由于SMM 模型具有較差的魯棒性和泛化能力，其在任一訓練樣本數下的分類正確率都比其他四種方法低，表明SMM 小樣本分類性能最差。

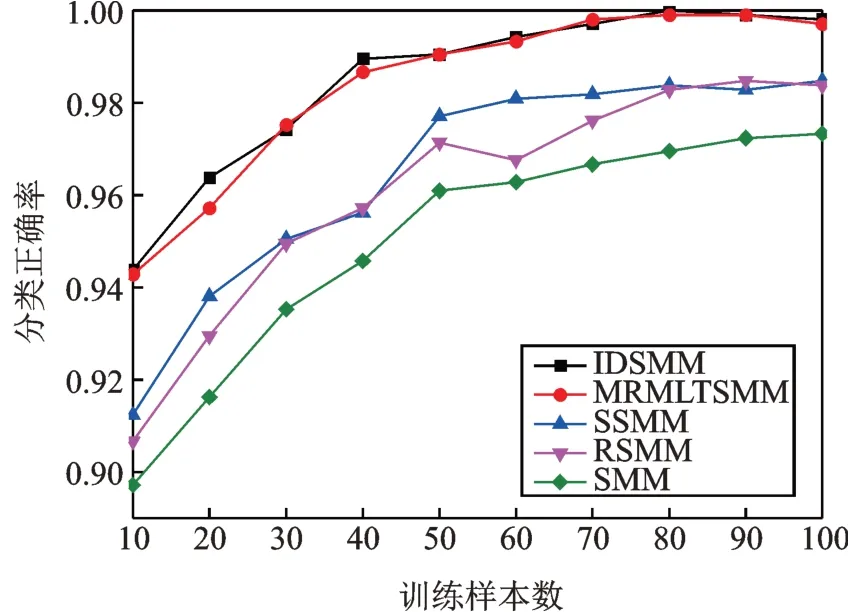
圖11 不同訓練樣本數的分類正確率Fig.11 Classification accuracy of different numbers of training samples

綜上所述，根據五種方法在5 種衡量指標下的對比結果可知，IDSMM 的診斷性能明顯優于SMM，RSMM，SSMM 和MRMLTSMM。IDSMM采用一種交互偏移超平面的方式構造兩個超平面，當數據較為復雜時，可以為每一類特征樣本構造一類超平面。同時，由于本類樣本所屬平面與異類樣本的距離被拉大，因此具有更好的分類性能。SMM作為一種平行超平面分類器，當輸入數據包含多種特征信息時，其無法有效構造合適的超平面。SSMM 構建模型的前提是回歸矩陣具有低秩特性，因此在面對大多數矩陣是多秩的情況下很難發揮模型本身的優勢，而IDSMM 引入了左右多秩投影矩陣，可以更好地解決該問題。相比其他平行超平面分類器，IDSMM 因其借助NHC 思想構造超平面的方式，在處理二分類問題尤其是復雜問題時具有明顯的優勢。

3 結論

本文提出一種交互偏移支持矩陣機（IDSMM）的矩陣分類方法。不同于傳統非平行超平面的構造形式，IDSMM 在建模過程中，在每個目標函數中加入偏移參數，以改變約束，構造出一對交互偏移超平面Tr(WT1X(1))+b1=1 和Tr(WT2X(2))+b2=-1。交互偏移超平面克服了復雜數據間的有效分割問題，并且每一個超平面距離異類樣本更遠，提高了模型的泛化能力。同時，IDSMM 使用左右投影矩陣構造目標函數，避免了數據過擬合問題。通過對兩個滾動軸承數據集進行實驗驗證，實驗結果表明，與SMM，RSMM，SSMM 和MRMLTSMM 相比，IDSMM 在滾動軸承故障診斷中具有更優異的性能。