含常數激勵非對稱Duffing系統的主共振響應及鞍結分岔研究

羅 鋼，侯 磊，任雙興，陳予恕

（哈爾濱工業大學航天學院，黑龍江哈爾濱 150001）

1 概述

在非線性振動系統中，常數激勵［1-2］是導致非對稱性的主要因素之一，例如，在旋轉機械中，裂紋轉子系統受重力作用［3-4］、軸承轉子系統受徑向載荷作用［5-7］、基礎運動及機動飛行轉子系統承受慣性載荷［8-11］等。非對稱性使得非線性振動系統的動力學特性相比于一般的對稱系統更加復雜，尤其是在非對稱因素十分顯著的情況下。

Carnegie 等［12］研究了重力對Duffing 系統2 次超諧共振的影響，表明重力使得恢復力產生不對稱性，勢能函數的冪律指數由奇數特征變為偶數特征。

含常數激勵非對稱Duffing 方程的一般形式如下：

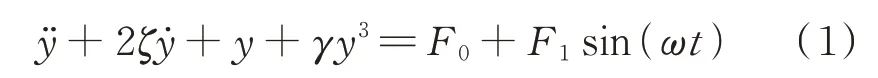
Hayashi［13］研究了參數取γ=ω=1 的情況，表明在一定參數條件下，當常數激勵F0在某一范圍內取值時，系統最多有5 個穩態解，能夠產生多次跳躍現象。

對于帶有平方非線性項的Helmholtz-Duffing方程：

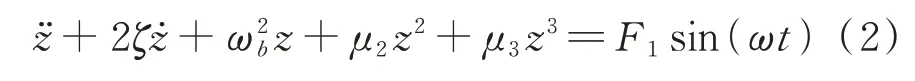
Ravindra 等［14］通過平移變換將其轉化為方程（1），通過解析求解表明平方非線性的存在使得具有硬特性的Duffing 系統產生剛度增強效應，使其幅頻曲線峰值點發生右移。Benedettini 等［15-17］系統研究了振動方程形如式（2）的懸索主共振響應、2 次和3 次超諧共振響應，以及1/2 次和1/3 次亞諧共振響應，表明這些共振響應中均存在軟硬特性變化和多值現象，并且由于平方非線性項的存在，2 次超諧共振顯著強于3 次超諧共振，1/2 次亞諧共振顯著強于1/3 次亞諧共振。Murata 等［18］利用突變理論研究了方程（2）的分岔特性，闡釋了跳躍現象及滯后現象的發生機制。Yagasaki［19-20］分別針對原子顯微鏡的尖端部分——微型懸臂梁和受線性反饋控制的單擺建立了形如方程（2）的動力學方程，利用二階平均法分析了主共振響應的分岔性質，并給出產生亞臨界鞍結分岔及超臨界鞍結分岔時的激勵幅值［21］，還采用一種推廣的亞諧Melnikov 方法研究了方程中出現的退化共振行為，表明退化共振一般會導致尖點分岔［22-23］。TIAN 等［24-25］發現在常數激勵作用下，光滑非連續振子的混沌吸引子與SD 振子有顯著區別。Kovacic 等［26-28］將一個準零剛度非線性隔振器模型的振動用方程（1）描述，對其主共振響應進行了細致的研究，表明在常數激勵的作用下，系統能夠表現出4 種不同的幅頻曲線類型，除了近似線性的單解類型和具有3 個穩態解的單彎曲類型，還存在具有3 個穩態解的雙彎曲類型以及具有5 個穩態解的雙彎曲類型。侯磊等［29］對方程（1）描述的非對稱Duffing 系統的骨架曲線和幅頻響應進行了研究，發現骨架曲線的形態表現為先向左微偏后轉為向右彎曲，對應的幅頻曲線在簡諧激勵幅值較小時表現為軟特性，當簡諧激勵幅值增大時表現出軟硬特性共存現象。此外，通過奇異性分析給出了該系統在常數激勵與簡諧激勵幅值不同組合下的6 種分岔模式［30］。

本文以形如方程（1）的含常數激勵的非對稱Duffing 系統為研究對象，求解強非線性Duffing 方程在常數激勵與簡諧激勵聯合作用下的主共振響應，重點研究常數激勵對系統鞍結分岔的影響規律。

2 主共振響應的近似解析求解與穩定性分析

2.1 諧波平衡法求解主共振響應

采用諧波平衡法求解方程（1）的主共振響應。由于方程（1）中存在常數激勵F0，其振動響應中會產生直流分量，其一階近似解具有如下形式：

式中A0為直流分量，A1為諧波響應的幅值，θ為初相位。

將式（3）代入式（1），令常數項、余弦項和正弦項系數分別為零，可得幅頻響應方程組：

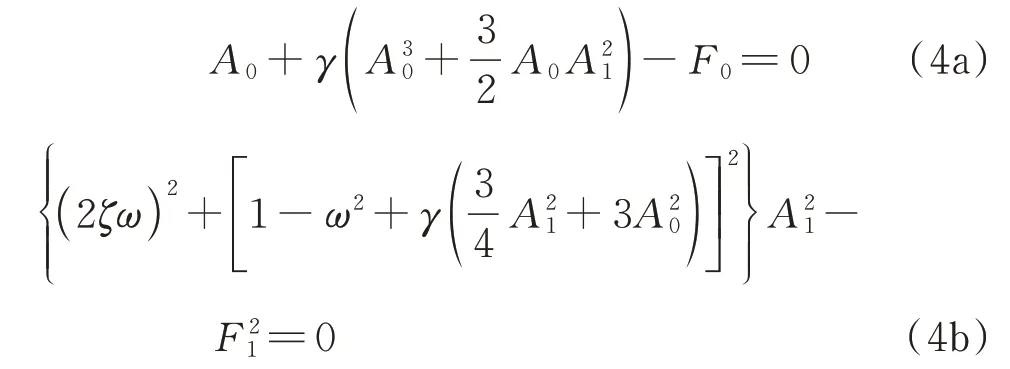
根據式（4a），A1與A0有如下關系：

將式（5）代入式（4b），可得關于A0的方程：

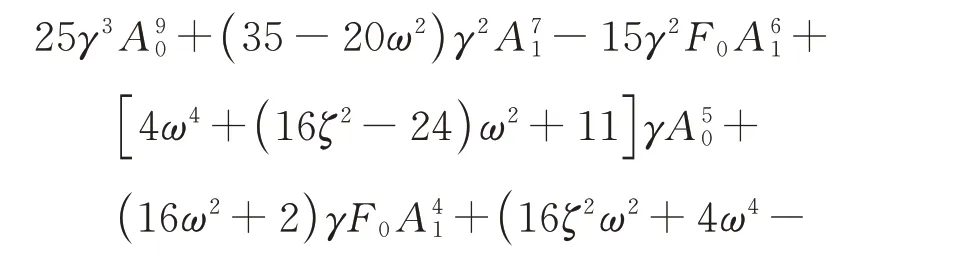
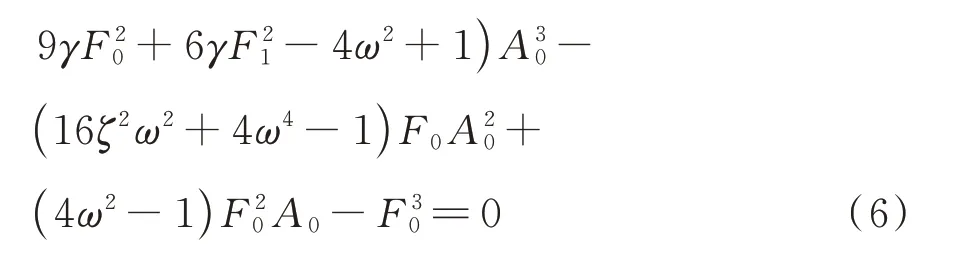
可見式（6）是關于A0的9 次方程。

根據笛卡爾符號法則，一元多項式方程具有正數解的個數要么等于其系數符號改變次數，要么比此次數小一個偶數。式（6）系數符號改變次數為5次，其具有正數解的數目為5 或3 或1，因而式（1）的主共振響應最多有5 個。

2.2 穩定性分析

采用Floquet 理論分析周期解的穩定性。在式（3）的基礎上增加一個小擾動u形成的擾動解如下：

將式（7）代入式（1），注意到y也是式（1）的解，可得基于解y的線性變分方程如下：

其中：

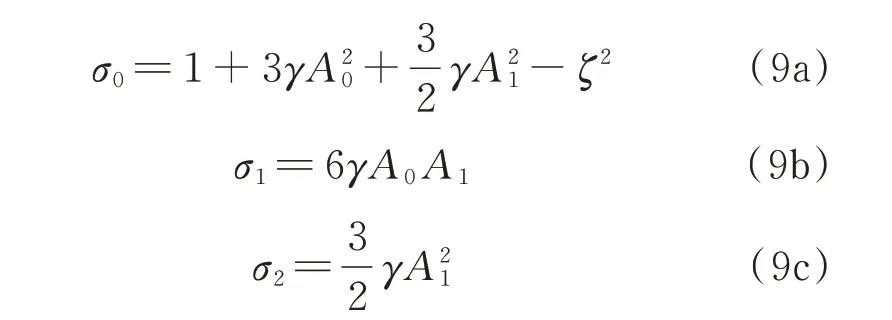
對式（8）作如下變換：

得到如下形式的Hill 方程：

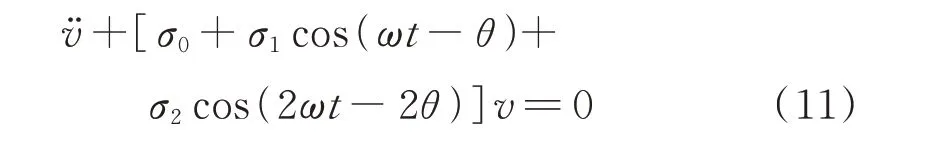
根據Hill 方程的相關理論，當激勵頻率與規范化固有頻率具有如下關系：

時，式（11）所代表的參激系統將在第n個不穩定區域發生共振。為了考察形如式（3）的解的穩定性，本文考慮第二個不穩定區域。可設式（11）的解的形式為：

式中μ為Floquet 特征指數，其實部符號決定式（11）零解的穩定性。

仍采用諧波平衡法，取一階近似，令常數項、余弦項和正弦項系數為零，得到如下方程組：

由于式（13）為非零解，則有：

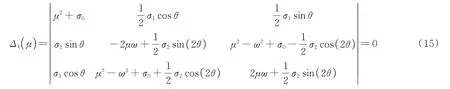
由Floquet 理論可知，方程（1）形如式（3）的周期解的穩定條件為-ζ±μ的實部小于零，又由于阻尼系數ζ＞0 且μ為實數或虛數，則穩定條件等價于ζ2＞μ2。結合式（15），可知穩定條件為Δ1(ζ)＞0，穩定邊界為Δ1(ζ)=0，其中：

將式（9）代入式（16）并整理，得穩定邊界：

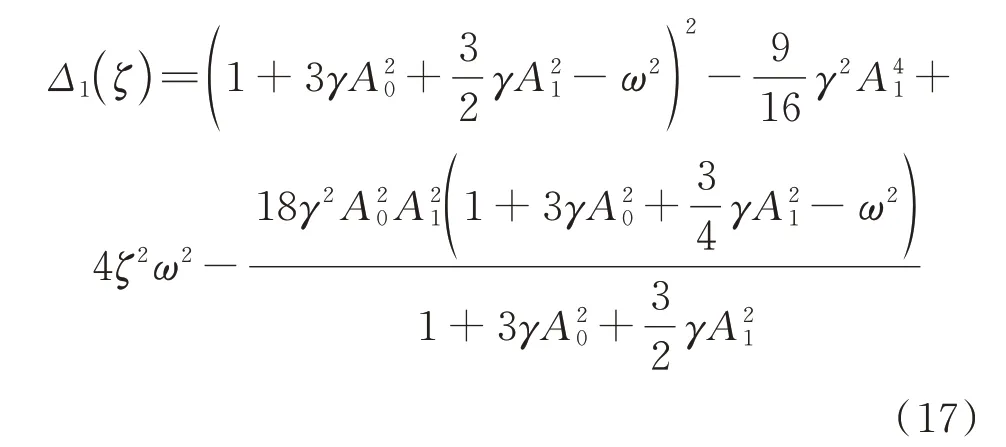
為了將周期解的穩定性反映到幅頻響應曲線上，將幅頻響應方程重新符號化如下：

傳說，對著樹洞講出你的心事，心情會釋然。找到你的樹洞，埋藏進所有的眼淚和哭聲，讓我為你守望。不知不覺中你就會長大。

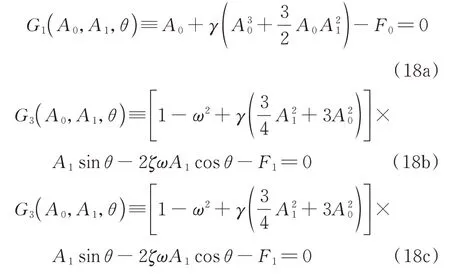
將式（18）關于頻率ω求全導數，并從中解出未知數?A0/?ω，?A1/?ω和?θ/?ω，得：

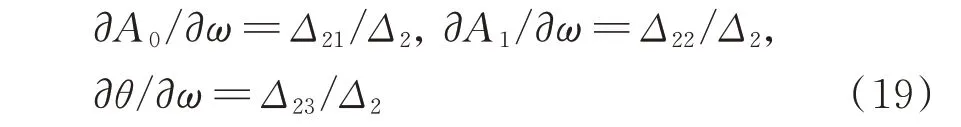
其中：

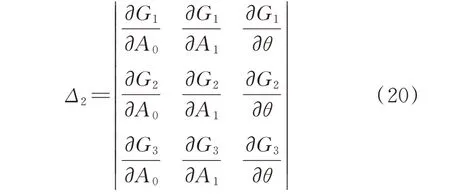
Δ2i(i=1，2，3)是用?G1/?ω，?G2/?ω和?G3/?ω的相關項替換行列式Δ2中第i列得到的新行列式。計算行列式Δ2并整理，得到：

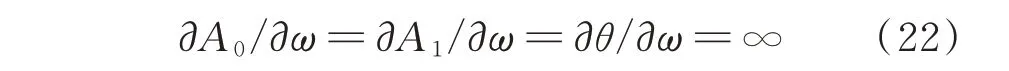
因此，當Δ1(ζ)=0 時，Δ2=0。結合式（19），在穩定邊界上有：也就是說，在幅頻響應曲線上，在穩定邊界點處的切線斜率為無窮大，即垂直于頻率軸。穩定邊界將穩定解所在區域與不穩定解所在區域分隔開，可以通過式（17）來判斷特定解的穩定性。

3 主共振響應中的非線性振動特性分析

3.1 主共振下的幅頻響應

以系統參數取ζ=0.015，γ=4，F1=0.05 為例，在常數激勵作用下，方程（1）主共振下的幅頻響應曲線會出現軟特性共振滯后區，隨著常數激勵的增大，軟特性共振滯后區不斷擴大，而原有的硬特性共振滯后區逐漸收縮直到完全消失，在這個演化過程中系統會表現出6 種類型的幅頻響應曲線，這在文獻［30］中有詳細論述。本文以F0=0.8 為例，給出系統最典型的具有5 解共存情況的幅頻響應曲線，如圖1所示，其中實線代表穩定解，虛線代表不穩定解，箭頭標示了正反向掃頻時幅值的變化方向及跳躍現象。由圖1 可見，隨著簡諧激勵頻率ω的增大，幅頻響應曲線先向左彎曲，后向右彎曲，形成一個軟特性共振滯后區和一個硬特性共振滯后區，且兩個共振滯后區有一部分重合區域，在重合區域內特定ω下系統有5 個周期解，其中3 個為穩定解，2個為不穩定解，而在兩個共振滯后區的非重合區域，特定ω下系統有3 個周期解，其中2 個為穩定解，1個為不穩定解。

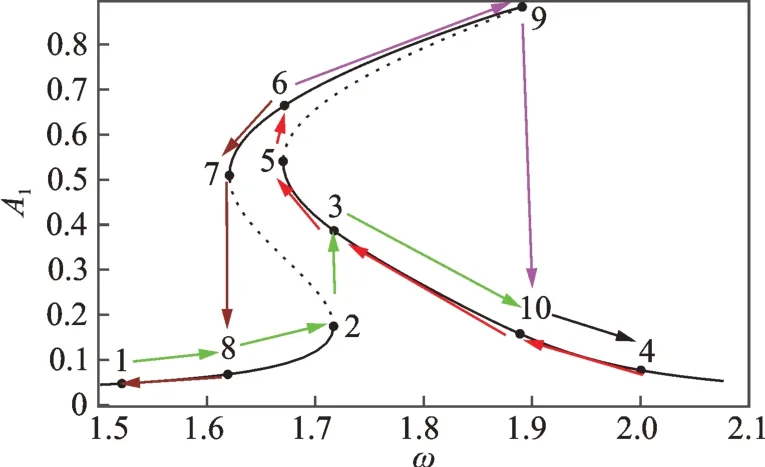
圖1 F0=0.8 時系統的幅頻響應曲線(ζ=0.015，γ=4，F1=0.05)Fig.1 Amplitude-frequency response when F0=0.8(ζ=0.015，γ=4，F1=0.05)

此外，圖1所示系統還存在復雜的跳躍現象。從點1 出發正向掃頻時，隨著簡諧激勵頻率ω的緩慢提高，系統振幅逐漸增大，經過點2 時振幅將跳躍到點3，此時若繼續提高ω，則振幅逐漸減小，直到點4。從點4 出發反向掃頻時，隨著ω的緩慢降低，系統振幅逐漸增大，經過點3 時不發生跳躍現象，而是振幅繼續逐漸增大，直到經過點5 時發生跳躍現象，系統振幅將跳躍到點6，此時若繼續降低ω，則系統振幅逐漸減小，直到點7 再次發生跳躍現象，系統振幅將跳躍到點8，隨著ω的進一步降低，系統振幅逐漸減小，回到點1。當系統振幅達到點6 時，若緩慢提高ω，則系統振幅會逐漸增大，直到點9 發生跳躍現象，系統振幅跳躍到點10。以ω=1.71 為例，此時系統為典型的5 解共存，通過四階龍格-庫塔法對系統求穩定解，得到系統在不同初始條件下的相圖和時間歷程曲線如圖2所示。

圖2 ω=1.71 時系統的相圖與時間歷程(ζ=0.015，γ=4，F0=0.8，F1=0.05)Fig.2 Phase diagrams and time histories when ω=1.71(ζ=0.015，γ=4，F0=0.8，F1=0.05)

Duffing 系統主共振下幅頻響應曲線上的跳躍點均是鞍結分岔點，軟特性共振滯后區和硬特性共振滯后區的左右邊界分別對應一個鞍結分岔點，即圖1 中的點2、點5、點7、點9 四個點。因此，研究系統的鞍結分岔特性有助于認識其復雜跳躍現象的機理。

3.2 鞍結分岔特性分析

鞍結分岔，也稱切線分岔或折疊分岔，是非線性動力學中最為基本的局部分岔模式之一，在分岔圖中分岔點處的切線鉛直是其典型的幾何特征，利用該特征可通過幅頻響應方程計算系統的鞍結分岔集，并據此對幅頻響應曲線進行分類。關于分岔分析更為詳細的方法，可參考文獻［31］。

圖3所示為系統參數取ζ=0.015，γ=4，F1=0.05 時，ω-F0平面上的鞍結分岔集。可見，鞍結分岔集由曲線ABC 和曲線FGH 組成，其中曲線ABC 為軟特性共振滯后區對應的鞍結分岔集，曲線FGH 為硬特性共振滯后區對應的鞍結分岔集。圖中還在每段分岔集曲線左右標示出了經過相應分岔點時系統周期解數目的變化情況，因此通過分析這些分岔集曲線可以掌握系統周期解數目增加或減少的具體情況。

圖3 ω-F0 平面上的鞍結分岔集Fig.3 Saddle-node bifurcation set on the ω-F0 plane

若以簡諧激勵頻率ω為分岔參數，則隨著ω的增大，當經過曲線AB 和DF 時，系統周期解的個數由1 個變為3 個，增加1 個穩定解和1 個不穩定解，此時系統共有2 個穩定解和1 個不穩定解。隨著ω的進一步增大，當經過曲線BD，CE 和EH 時，增加的2個周期解消失，系統周期解的個數由3 個變回1 個。

在鞍結分岔集曲線ABC 和曲線FGH 的交叉區域，隨著ω的增大，當經過曲線DG 時，系統周期解的個數由3 個變為5 個，增加1 個穩定解和1 個不穩定解，此時系統共有3 個穩定解和2 個不穩定解。隨著ω的進一步增大，當經過曲線DE 和EG 時，增加的2 個周期解消失，系統周期解的個數由5 個變回3 個。

因此，曲線DF，DE 和EH 圍成的區域為硬特性共振滯后區，系統的幅頻響應曲線有3 解，這與傳統的無常數激勵的Duffing系統的主共振特性一致。曲線AB，BD，DG 以及曲線CE，EG 圍成的區域為軟特性共振滯后區，系統的幅頻響應曲線有3 個解。曲線DE，DG，EG 圍成的區域為軟特性共振滯后區和硬特性共振滯后區的重疊區域，系統的幅頻響應曲線有5 個解。

當常數激勵F0較小時，系統幅頻響應曲線隨著ω的增大其解的個數會經歷1-3-1 的變化，此時系統僅有一個硬特性共振滯后區，與傳統的無常數激勵的Duffing系統的主共振特性一致。當F0的取值處于曲線BD 在縱軸的投影區域時，系統幅頻響應曲線隨著ω的增大其解的個數會經歷1-3-1-3-1 的變化，此時系統同時具有硬特性共振滯后區和軟特性共振滯后區，但兩個共振滯后區處于分離狀態。當F0的取值處于曲線DG 在縱軸的投影區域時，系統幅頻響應曲線隨著ω的增大其解的個數會經歷1-3-5-3-1 的變化，此時硬特性共振滯后區與軟特性共振滯后區有交叉。當F0更大時，硬特性共振滯后區消失，系統僅具有軟特性共振滯后區，幅頻響應曲線隨著ω的增大其解的個數會經歷1-3-1 的變化。

4 參數對鞍結分岔集的影響分析

4.1 阻尼的影響

圖4所示為系統參數取γ=4，F1=0.05，阻尼系數ζ分別取0.01，0.015，0.03，0.04 和0.06 時，ω-F0平面上的鞍結分岔集。可見，隨著阻尼系數的增大，系統的鞍結分岔集發生顯著變化，軟特性共振滯后區和硬特性共振滯后區均收縮變小，同時軟特性共振滯后區向平面的右上方移動，硬特性共振滯后區向平面的左下方移動，兩個共振滯后區的重疊區域也逐漸變小，直到兩個共振滯后區完全分離；當ζ=0.06 時，軟特性共振滯后區完全消失。表明阻尼的增大有利于抑制Duffing 系統的多解及振幅跳躍現象。

圖4 不同阻尼大小下ω-F0 平面上的鞍結分岔集(γ=4，F1=0.05)Fig.4 Saddle-node bifurcation sets with different damping on the ω-F0 plane(γ=4，F1=0.05)

4.2 簡諧激勵幅值的影響

圖5所示為系統參數取ζ=0.015，γ=4，簡諧激勵幅值F1分別取0.05，0.03，0.018，0.01 和0.008時，ω-F0平面上的鞍結分岔集。可見，隨著簡諧激勵幅值的減小，系統的鞍結分岔集發生顯著變化，其變化趨勢與阻尼系數增大時的變化趨勢相似，軟特性共振滯后區和硬特性共振滯后區均收縮變小，同時硬特性共振滯后區向平面的左下方移動，但軟特性共振滯后區向平面的右下方移動，兩個共振滯后區的重疊區域也逐漸變小直到兩個共振滯后區完全分離；當F1=0.008 時，軟特性共振滯后區完全消失。結果表明簡諧激勵幅值的減小也有利于抑制Duffing 系統的多解及振幅跳躍現象。

圖5 不同簡諧激勵幅值下ω-F0 平面上的近似鞍結分岔集Fig.5 Approximate saddle-node bifurcation sets with different harmonic excitation on the ω-F0 plane

5 結論

本文針對含常數激勵非對稱Duffing 系統開展了鞍結分岔特性研究，采用諧波平衡法求得系統在主共振下的周期解，采用Floquet 理論分析周期解的穩定性，利用幅頻響應曲線上鞍結分岔點處具有切線鉛直的幾何特征，計算了系統關于常數激勵和簡諧激勵頻率的鞍結分岔集，并分析了阻尼和簡諧激勵幅值對鞍結分岔集的影響規律，得到結論如下：

1）在特定參數條件下，系統的幅頻響應曲線先向左彎曲后向右彎曲，形成一個軟特性共振滯后區和一個硬特性共振滯后區，在兩個共振滯后區的重合區域內，系統具有5 解共存現象，5 個周期解中3個為穩定解，2 個為不穩定解。

2）在5 解共存情況下，系統幅頻響應曲線上表現出復雜的振動跳躍現象，在軟特性共振滯后區和硬特性共振滯后區的左右邊界上共形成4 個振動跳躍點，均為鞍結分岔點。

3）在常數激勵與簡諧激勵頻率構成的參數平面上，鞍結分岔集由兩條曲線組成，其中一條為軟特性共振滯后區對應的鞍結分岔集；另一條為硬特性共振滯后區對應的鞍結分岔集。兩條曲線包圍的參數區域為多解參數區，其中兩條曲線的交叉區域為5 解共存參數區。

4）隨著常數激勵的增大，系統幅頻響應曲線上表現出軟特性逐漸增強、硬特性逐漸變弱的現象，兩者對應的共振滯后區從分離到交叉，直到硬特性共振滯后區消失，其中在共振滯后區交叉的參數區存在5 解共存現象和復雜的振動跳躍現象。

5）增大系統阻尼或減小簡諧激勵幅值，系統的鞍結分岔集發生顯著變化，軟特性共振滯后區和硬特性共振滯后區均收縮變小，并且兩個共振滯后區的重疊區域也逐漸變小直到兩個共振滯后區完全分離，表明增大系統阻尼或減小簡諧激勵幅值有助于抑制系統主共振響應中的多解及復雜振動跳躍現象。