導管架用結構管應變時效試驗中應變量的計算
1 概述
應變時效是指金屬材料在加工生產過程中產生塑性變形,在高溫時效或長時間室溫時效作用下金屬材料的強度增加而韌性下降的現象
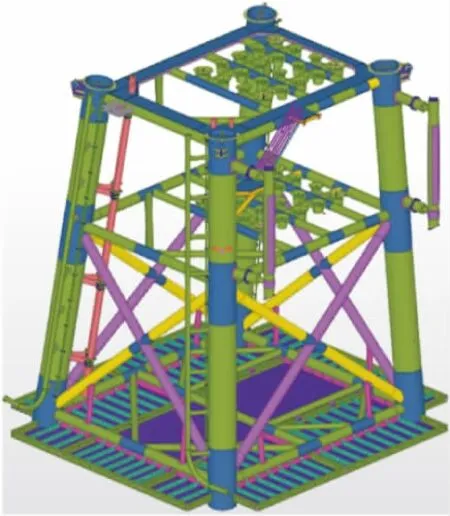
。導管架主要由大直徑結構鋼管構成,如圖1所示。導管架結構管采用三輥卷板機對鋼板進行卷管,采用埋弧焊進行焊接,鋼板在卷制成管的過程中會產生一定的應變量,焊接高溫會對周圍鋼材產生時效作用,因此導管架結構管在生產制造過程中必會產生明顯的人工應變時效現象。
后張法懸臂澆筑預應力連續梁張拉伸長值計算與分析……………………………………………………… 郭迎賓(8-98)
(2)數據挖掘階段,對于采集和預處理后的數據,首先要確定是數據挖掘目標和類型。在確定挖掘具體的任務后,可以采用相應的數據挖掘算法進行數據的挖掘,具體的算法接下來會詳細介紹數據挖掘的主要算法。經過數據挖掘過程后,會對挖掘的結果保存到數據庫后,以便于接下來的處理。
為了評價卷管工藝產生的應變時效對金屬材料性能的影響,導管架建造過程中需要依據相應的試驗標準進行應變時效試驗。應變時效試驗原理是分別測定鋼未經受規定應變和經受規定應變并人工時效后的沖擊吸收能量,采用公式計算出鋼的應變時效敏感性系數,表征鋼的應變時效敏感性
。
根據導管架常用的應變時效試驗標準GS EP STR 201和BV NR426—2006,應變時效試驗可采用工程應變時效和實驗室模擬兩種方法。實驗室模擬應變時效試驗主要采用實驗室設備儀器將被測樣品軸向拉伸至規定的最大線應變后進行250℃時效,工程應變時效試驗主要采用相同工藝卷制成品管后再進行250℃時效。工程應變時效試驗由于需要卷管、焊接等作業,存在試驗成本高和周期長等缺陷,因此應變時效試驗主要采用實驗室模擬試驗方法。應變量為實驗室模擬應變時效最重要的試驗參數,應變時效試驗標準給出的應變量計算公式均將厚度中心層作為應變中性層,這與現有鋼板彎曲過程中應變中性層內移理論相矛盾
,因此本研究針對卷管工藝應變量計算進行分析研究。
小學生處于人身心發展的初期階段,身心發展不成熟,但可塑性較強,所以,德育與心理健康教育相融合具有重要的現實基礎。另一方面,現代社會生活節奏較快,生活壓力較大,為了更好地適應將來的社會生活,也需要重視對學生的品格塑造與心理健康教育。教師要通過一定的德育工作與心理健康教育工作,掌握學生的心理發展走向與道德現狀,轉變傳統的教育方式,用宣泄法、疏導法等,有效地與學生進行溝通,這樣學生才能卸下心靈的重擔,主動接受教師的德育工作。
2 應變量計算假設及方法
2.1 基本假設
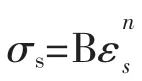
2.2 計算方法
將公式(16)整理后得
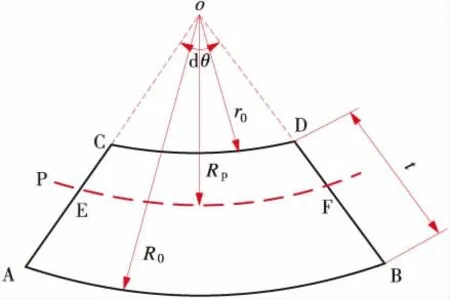
應變中性層在彎曲過程中由于應變量為零,其長度在彎曲過程中保持不變,因此可作為應變量計算的原始長度。在卷管上取一圓弧段,圓弧角度為θ,管外徑為R
,管內徑為r
,中性層半徑為R
,壁厚為t,如圖2所示。
蘇維埃文學的成功,是由于社會主義建設的成功而成功的。它的成長,就是我們社會主義建設的成功和成績的反映。我們的文學是各民族、各國家的文學中最年青的一種文學。然而它卻是最有思想、最先進和最革命的文學。這種先進的、有思想的而又革命的文學,能夠成為而且已經成為現實的,這就只有蘇維埃的文學——這是蘇聯社會主義建設所產出來的骨肉。[1]
應變中性層P的長度

沿AC橫截面外徑往內徑方向任一位置處的長度
表1中極差數據表明:單一因素的影響程度依次為:單體配比>反應溫度>引發劑加量>pH值。水泥堵劑的配方為:G級油井水泥60g+15%硅粉+2.0%緩凝劑+水,水灰比0.44,以下簡稱配方A。
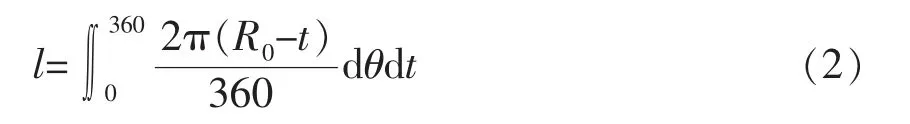
線應變量
東陽市境內以丘陵與盆地為主,會稽山大盤山、仙霞嶺延伸入境,形成三山夾兩盆的獨特地理環境。截至2017年底,東陽市擁有省級森林城鎮5個,市森林覆蓋率達到59.1%,林木覆蓋率為60.0%,為省級森林城市。為了能夠更好地了解東陽市森林古道的現狀,挖掘森林古道的價值,發現森林古道存在的問題,筆者對東陽市境內的森林古道進行了調查研究與分析,希望能為森林古道的保護與修復提供參考。
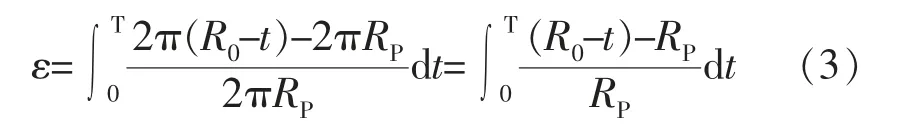
卷管平面彎曲的平衡方程式為
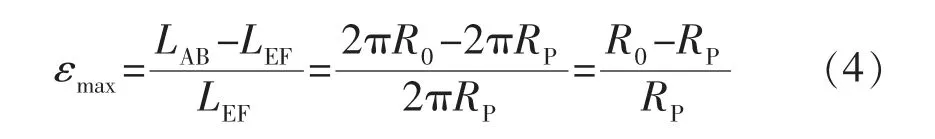
對于管徑和壁厚等卷管參數已知的情況下,從公式(4)中可以看出,最大線應變量計算的核心在于確定中性層半徑。
3 中性層理論計算分析
根據材料力學原理,對受力物體內的一般空間受力狀態進行分析,卷管過程中應變分布情況如圖3所示,分別產生切向、徑向和寬度三個方向的主應變
,根據應變量定義進行理論推導計算。

根據公式(2)推理,寬板彎曲時在寬度方向變形近似為零,其寬度方向應變,即鋼板彎曲可簡化為只有切向應變和徑向應變的平面應變狀態,其中:
切向應變

其中,當r>R
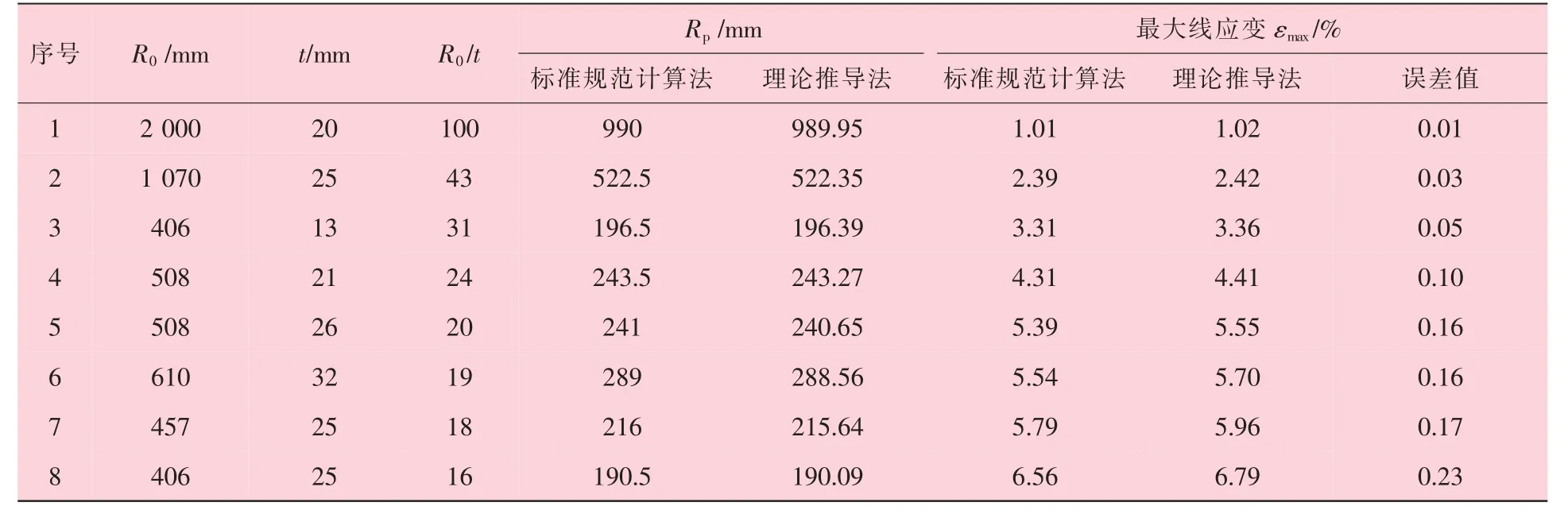
時取“+”號,當r 時取“-”號。 (4)選擇適宜間距的導向裝置緊貼試件表面,握住刀具,使刀垂直于試樣表面,對刀具均勻施力,并以均勻的切割速度移動刀具,使其在涂層上形成規定的切割數。所有切割都應劃透至基材表面; 由于鋼板在卷制彎曲過程中滿足金屬材料塑性變形時體積保持不變原則,即 將公式 (5)和 (6)代入 (7)中,其徑向應變,即 由于卷管過程中金屬材料處于兩向或三向應力狀態,需采用屈服準則判定所有應力分量。根據米塞斯屈服準則 根據米塞斯屈服準則定義的等效應力σ 和ε 等效應變表達式為 比爾會在那里等他的,他們會順著狄斯河向南劃到大熊湖。接著,他們就會在湖里朝南方劃,一直朝南,直到麥肯齊河。到了那里,他們還要朝著南方,繼續朝南方走去,那么冬天就怎么也趕不上他們了。讓湍流結冰吧,讓天氣變得更凜冽吧,他們會向南走到一個暖和的赫德森灣公司的站頭,那兒不僅樹木長得高大茂盛,吃的東西也多得不得了。 將公式(11)和公式(12)合并后,得 將公式(8)代入公式(13),得 Policeman:Why didn't you shout for help when youwere robbed ofyourwatch? 鋼板在外載荷作用下發生彎曲,其外側發生拉伸變形,而內側發生壓縮變形。當某一截面處于拉伸變形向壓縮變形過渡時,該截面既不產生拉伸應變也不產生壓縮應變,即為應變中性層P 。從應變中性層分別向外徑和內徑延伸,其應變量分別為拉應變和壓應變,且應變量具有連續性。 教師根據各小組合作學練情況,通過隨機抽組或小組自薦的形式按一定的順序展示各自的學練成果,并針對展示中存在的問題,進行點評與啟發,提升學生的技能水平。所以此環節,展示是主線,點評是關鍵。 徑向應變 從公式(3)中不難看出,無論是壓應變還是拉應變,均沿著應變中性層具有連續性。依據應變時效試驗標準要求,對于實驗室模擬應變時效試驗,取實際工況下的最大應變量值。根據公式(2),在t=0時,即卷管外表面處,此時為最大線應變量 隨著人力資源越來越緊張,目前市場上臨時工薪酬也在水漲船高,而隨著各大醫院的不斷發展壯大,醫院后勤所使用臨時工的人數也越來越多,而且基本上所從事的也是比較辛苦的體力需求較大的工作,如食堂、洗衣房、水電維修、衛生保潔等。工作時間長、工作量大、工作內容枯燥乏味,并且還經常會有投訴等問題產生。但醫院由于管理體制的緣故臨時工還不能從醫院的發展壯大中得到充分的實惠,薪酬普遍偏低。而且薪酬結構也不盡合理,傳統的“大鍋飯”政策,導致平均主義盛行,干好干壞,干多干少薪酬基本都一樣,造成臨時工心理上的不平衡,很容易像消極怠工的員工學習并在工作中產生馬虎敷衍的情緒,嚴重影響了臨時工工作的積極性和熱情。 將公式(17)代入公式(18)中,對r積分得 將公式(14)和(15)代入公式(3),得 式中:C——積分常數。 在卷管彎曲的外邊界上,當r=R 時,σ =0,由公式(19)積分可得 在卷管彎曲的內邊界上,當r=r 時,σ =0,由公式(19)積分可得 對于邊界條件處等效應力均為0,因此公式(20)和公式(21)相等,可得 依據上述應變中性層理論推導結果,將公式(22)帶入公式(4)中,最大線應變計算公式為 應變時效試驗常用的標準規范中采用簡化公式進行應變量計算,常見的標準規范計算公式參照道達爾公司標準GSEPSTR 201《海洋結構鋼材料》,標準中明確規定應變量應為冷成型所達到的最大應變量,計算公式為 式中:t——鋼板厚度,mm; D ——卷管后鋼板中心厚度對應的直徑。 法國船級社規范BV NR426《海上鋼結構構筑物和安裝建造規范》中,對于冷成形應變量計算公式為 公式(24)和公式(25)的分析推導在標準中均未給出詳細的過程,但根據公式中采用厚度中心層等參數,上述公式推導極有可能是基于應變中性層與厚度中心層一致的情況下進行理論推導。不妨假設上述公式是基于應變中性層為厚度中心層位置,即D =2R 成立,進行簡單的反向推導,其公式推導過程如下 最大線應變 將上述公式整理簡化,得 推導出來的公式(27)和公式(28)與標準計算公式(24)和公式(25)完全一致,因此,可以確定標準計算公式則是簡單的將厚度中心層作為應變中性層簡化處理后進行計算。 現有的大量理論研究均表明應變中性層在鋼板彎曲過程中會產生一定的內移 ,標準計算公式(24)和(25)是簡單地將厚度中心層作為應變中性層進行計算,必將導致計算公式(23)、(24)、 (25)的計算結果存在一定的差距,以某一導管架項目的卷管工藝參數進行計算比對分析,見表1。 水庫樞紐由大壩、溢洪道、輸水洞、泄洪洞和水電站等五部分組成。大壩為漿砌石重力墻式堆石壩,壩高46 m,長350 m。 從表1的數據可知,理論推導法計算出的最大線應變大于標準規范計算法,且隨著卷管外徑與壁厚比值越小,兩種方法計算出的最大線應變誤差值越大。理論推導法計算出的應變中性層位置小于厚度中心層位置,與板彎曲過程中應變中性層會產生內移的研究理論是一致的,表明理論推導的公式具有一定的科學性和合理性,而采用標準規范計算法進行計算存在一定的計算誤差。 應變時效試驗作為一項評價應變時效現象對金屬材料力學性能影響的重要檢測內容,隨著我國海洋石油工程裝備不斷向深水發展,應變時效試驗在海洋石油工程行業逐漸被重視。采用實驗室模擬應變時效試驗時,最重要的一項環節就是應變量的計算及試驗過程中應變量的控制。 通過對卷管彎曲應力應變分析,理論推導出最大線應變計算公式,并與現有標準中應變量計算方法進行對比分析。采用理論公式推導法計算的結果更加趨于實際情況,也符合應變中性層內移這一普遍認可的研究理論。因此,本研究推導出的理論公式在卷管工藝應變量計算中更加科學合理,可在應變時效試驗過程中予以推廣運用。 [1]張才毅,許中華,高珊.40 kg級高強度低溫韌性船板鋼的應變時效試驗研究[J].寶鋼技術,2015(2):18-22. [2]潘中德,龔娜,武會賓.S355厚規格鋼板應變時效行為研究[J].熱加工工藝,2017,46(24):119-121. [3]溫永紅,唐獲,武會賓,等.F40級船板鋼的應變時效行為[J].北京科技大學學報,2008,30(11):1244-1248. [4]侯登義,徐洪慶,陳曄.NVB級船板應變時效敏感性試驗[J].鋼鐵釩鈦,2008,29(1):34-37. [5]彭寧琦,史術華,羅登,等.應變時效對大口徑X80管線鋼拉伸性能的影響[J].機械工程材料,2018,42(6):42-45. [6]吳海鳳,鄭磊.預應變量和時效溫度對X80管線鋼性能的影響[J].材料熱處理技術,2009,38(10):166-169. [7]徐衛星,徐惟誠,陸海兵.預拉伸樣坯尺寸對應變時效敏感性試驗結果的影響[J].理化檢驗-物理分冊,2017,53(3):185-187. [8]中華人民共和國國家質量監督檢驗檢疫總局,中國國家標準化管理委員會.鋼的應變時效敏感性試驗方法(夏比沖擊法):GB/T 4160—2004[S].北京:中國標準出版社,2004. [9]官英平,趙軍.板料彈塑性彎曲應力應變中性層位置關系探討[J].塑料工程學報,2002,9(2):39-41. [10]張子騫,楊會林,田永利.薄壁管材矯直過程應變中性層偏移模型與分析[J].中國機械工程,2013,24(10):1390-1395. [11]鄒錫鈞,楊清春.彎曲件中性層的位于與展開長度的計算[J].機械工程師,1992(4):11-12. [12]戴宏勝,龔曙光,彭炎榮,等.寬板塑性彎曲應變增量中性層的分析[J].塑性工程學報,2010,17(3):81-84. [13]孫訓芳,方孝淑,關來泰.材料力學(1)[M].北京:高等教育出版社,2009.



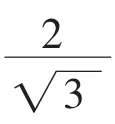

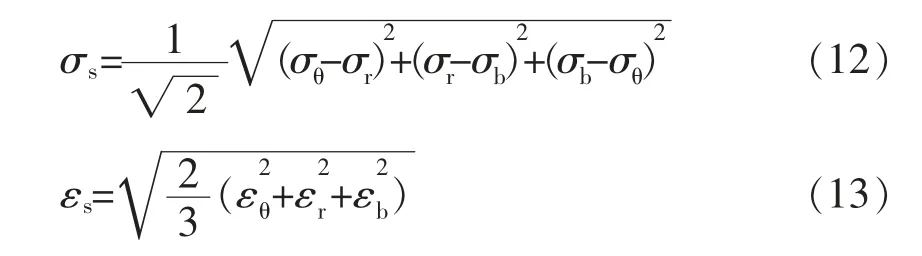
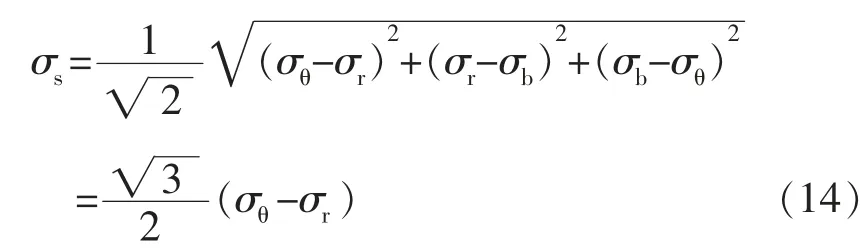
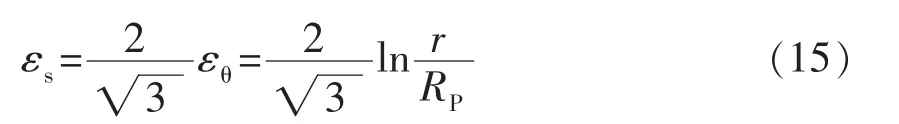
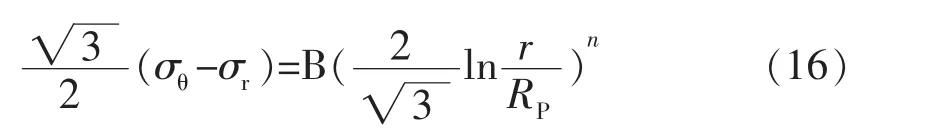



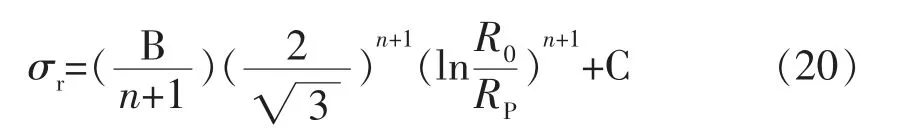
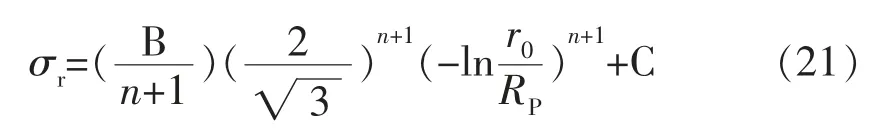

4 應變量計算方法對比分析
4.1 理論公式

4.2 標準公式


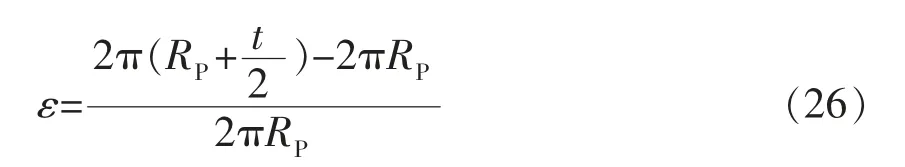


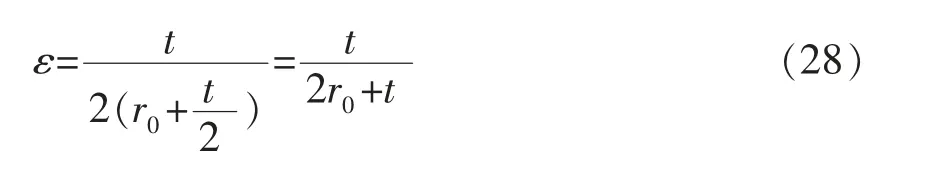
4.3 計算數據對比
5 結束語

