基于NSGA-Ⅱ的老舊小區改造方案優選

何琴琴， 李希勝， 萬寅子

(南京林業大學土木工程學院， 南京 210037)

老舊小區指建成于2000年以前的居民住宅，這類小區受當時建設條件的限制，建筑質量問題突出，基礎設施老化且落后[1]。隨著時間的推移，老舊小區嚴重影響了居民的生活質量。近年來，國家及各地方出臺了老舊小區改造的相關政策。2020年7月，國務院辦公廳印發《關于全面推進城鎮老舊小區改造工作的指導意見》，提出到“十四五”期末，結合各地實際，力爭基本完成城鎮老舊小區改造任務。老舊小區改造工程在政策引導、時代需求下如火如荼地展開。

在改造過程中，改造方案的選擇涉及多方利益，并對小區后期的管理產生深遠影響。針對改造方案的優選，中外學者已有相應的研究。李奕锜等[2]運用蒙特卡洛模擬探索老舊小區改造潛力測算與“保留、更新、重建”三種更新方案之間的聯系；李強年等[3]將多屬性決策與節能改造方案優選聯系，建立基于上升有序加權歐式平均算子的方案優選模型，求解指標屬性決策值，確定方案；劉龍等[4]利用模糊綜合評價法，對冷熱源改造方案進行優選；田穩苓等[5]以凈現值為目標對圍護結構節能改造方案進行優選；高源等[6]以采暖碳排放、采暖季室內熱舒適及改造全局成本增量為目標，對農宅低碳化改造進行方案優選；Mejjaouli等[7]利用混合整數線性規劃，以預算、熱舒適度和照明水平作為約束條件，以生命周期成本為目標，對節能改造策略進行方案優選；Fan等[8]提出一種用于建筑圍護結構改造的多目標優化模型，利用加權求和法將多目標轉換為單目標，并通過遺傳算法進行求解；李義廣[9]利用層次分析法及熵值法組合賦權對既有砌體結構抗震加固方案進行優選；高英博等[10]利用DeST-h軟件模擬分析不同墻體隨保溫層厚度的增加實現的節能效果，為確定墻體選用保溫層材料的厚度提供參考。

從以往有關老舊小區改造方案優選研究來看，存在以下特點：其一，目標單一，大多研究圍繞節能、成本、經濟效益等單個目標或者將多目標轉化為單目標展開研究；其二，研究內容單一，僅針對某一分部分項工程，如針對圍護結構、砌體抗震等，未從改造項目總體角度出發，考慮項目改造內容的具體方案。為此，本文研究在老舊小區改造內容優先級分析的基礎上[11]，進而確定改造項目分部分項工程的工期、成本和質量目標，從建設者和居民需求角度出發，建立工期、質量、成本的多目標優化模型，利用非支配排序遺傳算法(NSGA-Ⅱ)對多種方案進行方案優選，為決策者提供依據。

1 老舊小區改造方案優選

1.1 改造方案及目標的多樣性

老舊小區因其地緣、建造時間等不同，選擇的改造內容有所不同。在確定改造項目的改造內容后，每一個改造內容，由于其材料、工藝方式、功能等有多種選擇，從而組成多種改造方案。例如，某改造工程需要對外墻、窗戶、屋面三項進行改造，其中外墻有m種改造方案，窗戶有n種改造方案，屋面有i種改造方案，則經組合后，該改造工程有m×n×i種改造方案。

以目標為導向，進行方案優選，能夠有效地提高方案質量。從項目管理的角度看，類似于新建項目，老舊小區改造方案的工期、成本、質量三大目標通常作為方案綜合決策的依據[5]。改造項目的工期、成本、質量三個目標之間的關系是互斥的，適用帕累托最優法則進行方案優選。

1.2 方案優選程序

對改造方案進行優選，可有效避免改造方案同質化，而且有助于吸引老舊小區改造利益相關者的積極參與，提高改造質量。

方案優選流程圖如圖1所示，具體步驟如下。

(1)多方案構造。依據小區建筑設施部位與功能將改造內容進行分類[11]，結合擬改造項目的具體情況，對隸屬層級內容進行初步設計。

(2)多方案屬性定義。所謂屬性定義，就是預估擬改造內容的工期、成本、質量等信息，即擬改造項目的分部分項工程的預估工期、成本和質量信息。工期、成本可按定額法、統計法或經驗法確定；質量通過專家打分法確定。本文案例中工期主要由工程師依據現有的資源(機械臺班、人工等)及自身經驗確定；成本劃分為直接費和間接費，直接費由定額法進行計算，間接費由工程師依據經驗確定單日工程間接費；質量由5位經驗豐富的專家對各改造內容進行打分，求解平均值。

(3)建立多目標優化模型。通過改造方案描述、相關規范、問卷調查等對決策目標定量，建立目標函數。在進行方案優選時，選用工期、成本、質量為決策目標變量，項目分部分項工程即具體改造內容構成模型的決策變量。

圖1 方案優選程序圖Fig.1 Diagram of the program optimization program

(4)優化模型求解。基于第三步的目標函數及相關參數信息，利用非支配排序遺傳算法(NSGA-Ⅱ)進行多目標優化，得出Pareto最優解集。

(5)確定項目方案。決策者依據Pareto解集，結合自身偏好，選擇最終方案。

2 基于NSGA-Ⅱ算法的老舊小區改造多目標優化模型

針對多目標的求解常用的方法包括兩種：一是將多目標轉換為單目標，但這種方法難以統一各個函數量綱，易造成優化問題魯棒性差；二是求帕累托解集，可以求得多個最優解，解的優劣性可以得到較好的保證。從改造項目總體角度出發，以工期、成本、質量為目標，建立老舊小區改造方案優選的工期-質量-成本均衡優化的數學模型，并利用快速非支配排序遺傳算法(NSGA-Ⅱ)對模型進行求Pareto最優解集。

2.1 模型基本假設

由于改造內容所屬類別不同，從而存在引起各類復雜問題的可能，為了便于問題優化，做出如下假設。

(1)假設相鄰改造內容在改造過程中無時間間隔和距離間隔。

(2)假設每種改造內容只能選擇一種改造方案。

(3)假設改造過程中不存在人員窩工現象。

(4)假設每日所耗費的間接費用相同，一個項目的間接費用取決于其工期。

(5)假設改造成本計算不考慮通貨膨脹、匯率浮動等情況。

(6)假設工程在改造過程中無不可抗力的意外發生。

2.2 目標函數及約束條件

(1)工期最短。老舊小區在改造過程中，對小區居民的日常生活造成影響，同時對于建設方來說，工期的延長可能會造成成本的提高，因而工期最短為目標之一。關鍵路徑為網絡計劃圖中工期最長的路徑，其目標函數為

(1)

約束條件為

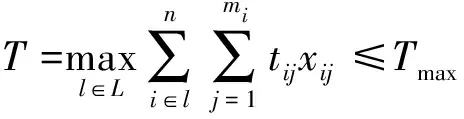
(2)

(3)

式中：T為項目總工期；i為改造內容；j為改造內容方案；n為改造內容總數；mi為改造內容i有m種改造方案；L為網絡圖中所有的線路；l為網絡圖中的關鍵路線；tij為第i項改造內容第j個改造方案；xij為索引變量，當xij=1時，表示第i項改造內容采用第j種改造方案，當xij=0時，表示第i項改造內容不采用第j種改造方案；Tmax為改造項目規定的最大工期。

(2)成本最低。老舊小區改造資金需求量大、居民出資意愿低、吸引社會參與難[12]。合理地控制成本能夠幫助利益相關者之間避免爭端。總成本指完成改造項目所花費的各項費用之和，歸類為直接費和間接費。其中直接費包括人工費、材料費、機械使用費；間接費包括項目管理費、利息、稅金等相關費用。其目標函數為

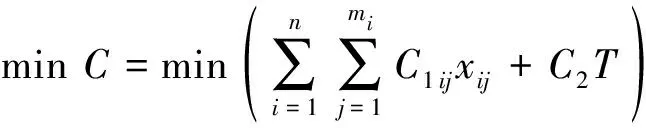
(4)

約束條件為

(5)

式中：C為改造總成本；C1為改造內容的直接成本；C2為改造內容的間接成本；C1ij為第i項改造內容第j種改造方式的直接成本；Cmax為改造項目規定的最高成本。

(3)質量最高。老舊小區改造工程由于各改造方案的工藝、材料不同，質量也有所差異。本文采用專家打分法，將改造方案的質量量化。邀請5位專家對不同的改造內容的質量權重以及對不同的改造方案進行打分，最后進行加權求和。其目標函數為

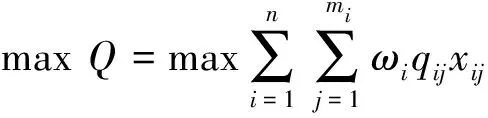
(6)

約束條件為

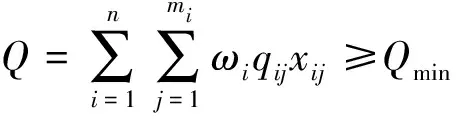
(7)

qij≥qi0

(8)

式中：Q為工程總質量；ωi為第i項改造內容占所有改造內容的權重系數；qij為第i項改造內容第j個改造方案的質量得分；qi0為第i個改造內容的質量標準；Qmin為項目所要求的最低質量。

3 多目標遺傳算法求解

3.1 非支配排序遺傳算法(NSGA-Ⅱ)基本原理

遺傳算法主要借鑒生物的進化思想，模擬自然選擇和自然遺傳的過程。遺傳算法能夠搜索解決方案空間的不同區域，使我們可以找到針對非凸、連續等問題的多樣化解決方案集。1994年Srinivas等[13]提出非劣分層演化算法，依據Pareto最優概念進行多目標演化。基于此，2002年Deb等[14]提出了非支配排序遺傳算法(NSGA-Ⅱ)，該算法能夠對種群中每個個體按Pareto優先順序進行排序。NSGA-Ⅱ采用精英策略，擇優保留當前為止所獲得的非支配解，且其中部分優秀的個體也能夠通過選擇策略被復制到下一個種群。使用NSGA-Ⅱ具有運行速度快，解集的收斂性好的優點，求解多目標問題能夠使帕累托最優前沿附近更好地收斂。

3.2 算法流程

采用整數編碼的方法。每條染色體表示為該改造工程的一種改造方案，基因的位置及基因的值分別表示為改造內容編號及該改造內容所選擇的改造方案編號，每個改造內容的方案數量作為基因的選擇。具體如圖2所示。流程圖如圖3所示，算法流程如下。

(1)產生初始種群。讀取老舊小區改造方案的目標函數，將決策變量初始化種群。

(2)非支配排序和擁擠度計算。

(3)選擇。選用錦標賽選擇函數，確定每次選擇的個體數量，保證每個個體被選擇的概率相同，同時避免選擇相同的個體，通過序值和擁擠距離的計算，選擇適應度最好的個體進入下一代種群。

(4)交叉與變異。新的個體結合父代的個體特性以及以一定概率隨機的改變串結構中某個串的值，得到新一代的個體。

(5)子代和父代個體融合。

(6)融合種群非支配排序和擁擠度計算。非支配排序的目的是為了使得解更加接近Pareto最優解，這是一個適應值分級過程。經過一輪輪排序，種群中的個體被分配到不同的前端。接著計算前端的擁擠距離，擁擠距離是指同一前端內個體與其相鄰個體的距離。

(7)終止條件。設Gen為迭代參數，當Gen達到程序設定的迭代次數時，終止條件，輸出結果。

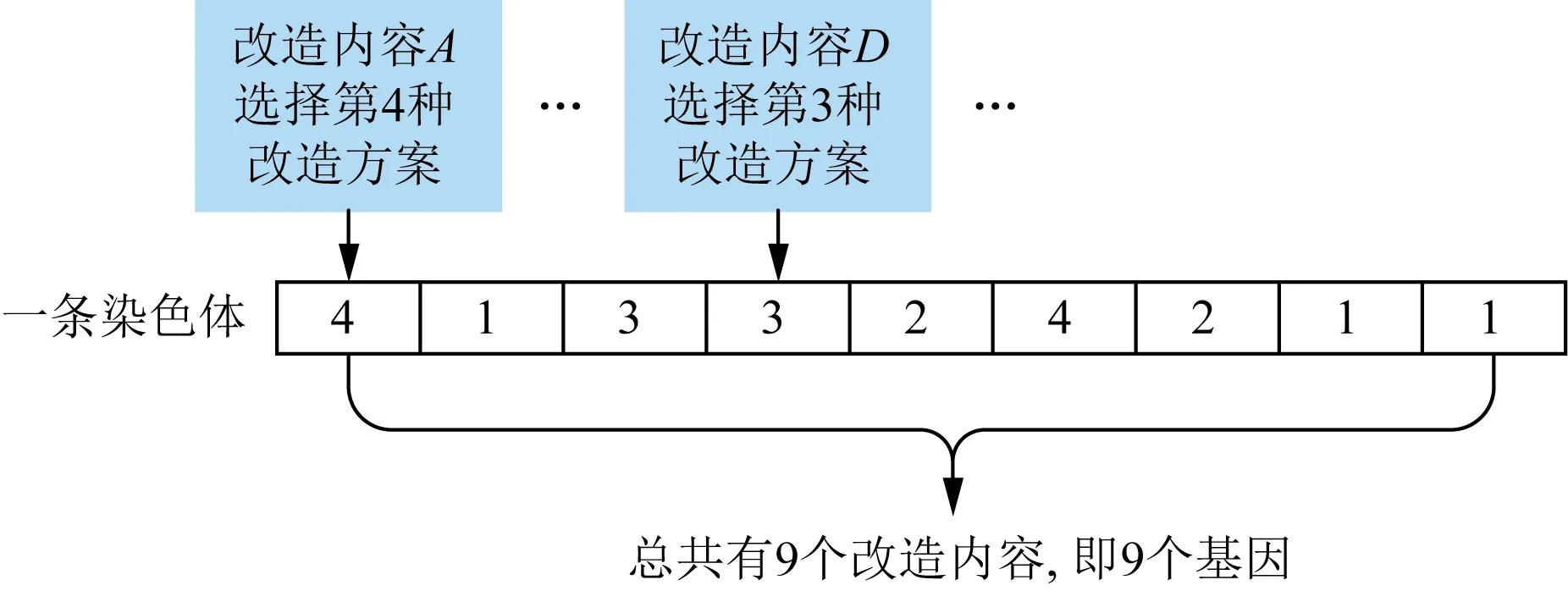
圖2 染色體整數編碼Fig.2 Chromosome integer coding

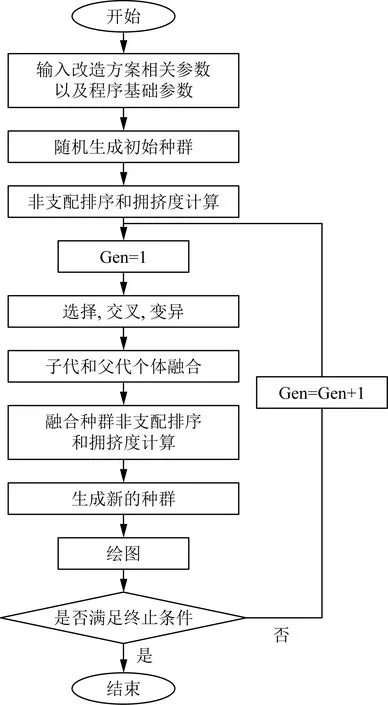
圖3 算法流程圖Fig.3 Algorithm flow chart

4 案例分析

4.1 項目概況

以南京市某老舊小區為例，該小區建于1992年，占地面積約11 萬m2，外立面屋頂等破損嚴重，小區居民改造意愿強烈。小區改造內容主要包括9 項，各項內容有多種改造方案，該老舊小區各改造內容的質量權重系數以及不同改造方案的質量得分由5 名經驗豐富的專家進行打分。各改造方案的直接成本、質量權重系數及各方案平均得分如表1所示，改造項目的網絡計劃圖如圖4所示。該項工程間接成本按3 500 元/d計算，工期至多165 d，成本至多2 400 萬元，工程綜合質量最低88 分，每個改造方案的質量得分最低87 分。

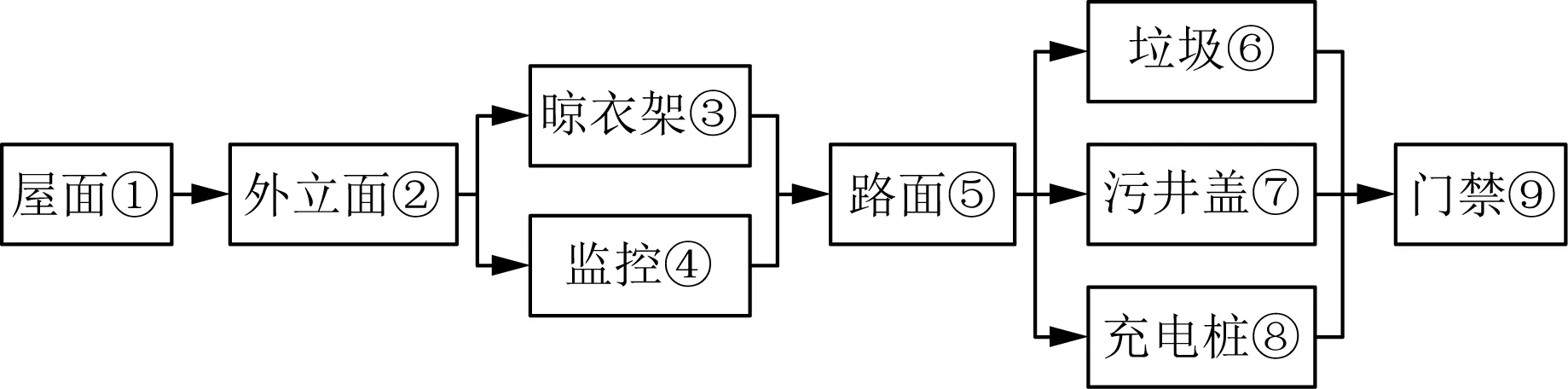
圖4 改造工程網絡計劃圖Fig.4 Network plan of the renovation project

4.2 模型求解

利用MATLAB軟件編寫遺傳算法程序，將表1中的數據錄入，并設定遺傳算法基礎參數：種群規模為50，迭代次數為200，交叉概率Pc為0.8，變異概率Pm為0.2，目標函數個數為3。經過200 次迭代，最終得到39 個帕累托解，圖5為帕累托最優解集三維圖，表2為部分帕累托最優解。

表1 南京市某老舊小區改造方案相關參數Table 1 Relevant parameters of the renovation plan of an old community in Nanjing

4.3 結果分析

根據方案組合，能夠得到82 944 種改造方案，通過工期-成本-質量的多目標優化后，精選出39 種方案，幫助決策者快速篩選出符合自身目標的方案，提升方案尋優效率。根據圖5中帕累托最優解集三維圖，可以觀察到總體趨勢呈現出隨著成本的增加，質量得到提高，工期相對延長。但也有部分解在成本增加的同時，質量或者工期未增加，反而有所下降。觀察解集，工期最少129 d，最多149 d，成本最低21 047 018.92 元，最高23 459 958.35元，質量得分最低88.718，最高為91.863 2。所得方案均在項目要求范圍之內，均為最優方案，決策者根據自身的財力、資源、偏向選擇方案。

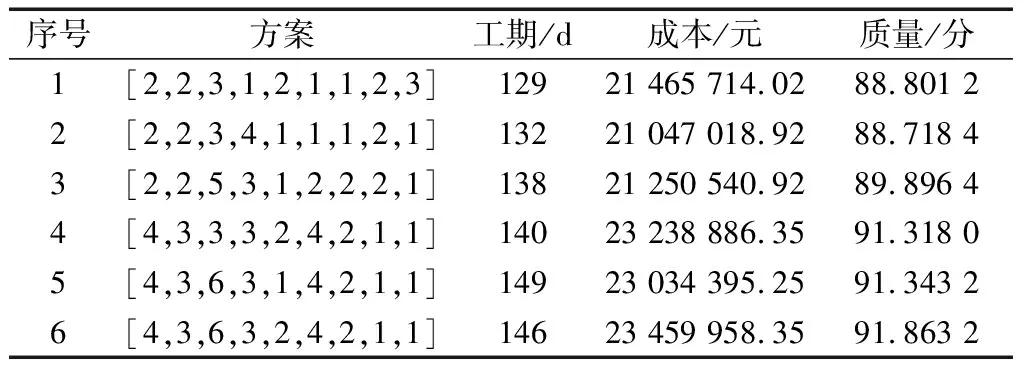
表2 部分帕累托最優解Table 2 Partial Pareto optimal solutions

5 結論

老舊小區改造方案優選是老舊小區改造前期的重要工作之一。由于在改造過程中，涉及多方利益，而無法達到平衡。以南京市某老舊小區為例，以工期、成本、質量為目標建立老舊小區改造方案的優化模型，并通過NSGA-Ⅱ求解，結果表明通過該優選方式進行方案能夠提高尋優效率，幫助決策者快速過濾出多種優選方案，也使得優選出的方案更具說服力。本文算法有待優化，此外，本文選擇的目標為工程最常見的三大目標，對于節能等目標的優化模型未涉及。針對以上不足，關于老舊小區方案優選的研究仍需繼續深入。

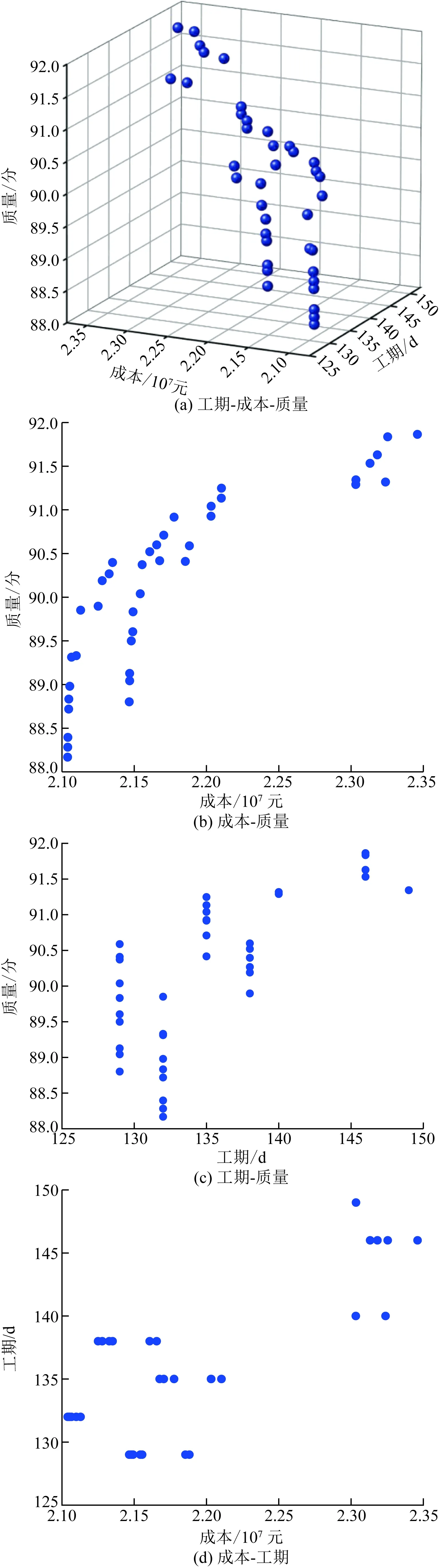
圖5 帕累托最優解集三維圖Fig.5 Three-dimensional diagram of Pareto optimal solution set