交換BCK-代數(shù)的新型軟（素）理想

黃 昱，廖祖華

1.無錫太湖學(xué)院 基礎(chǔ)課教學(xué)部，江蘇 無錫214064

2.江南大學(xué) 理學(xué)院，江蘇 無錫214122

非經(jīng)典邏輯及相關(guān)代數(shù)結(jié)構(gòu)是人工智能的數(shù)學(xué)基礎(chǔ)之一，其中的BCK/BCI-代數(shù)自Imai等提出以來，不斷得到學(xué)者們的廣泛研究。Xi把模糊集應(yīng)用于BCK-代數(shù),并給出BCK-代數(shù)的模糊理想、模糊關(guān)聯(lián)理想等概念。彭家寅把擾動模糊集應(yīng)用于BCI-代數(shù)中，研究了BCI-代數(shù)的擾動模糊-理想。軟集的理論是處理不確定性問題的重要數(shù)學(xué)工具之一。Jun 等把軟集應(yīng)用于BCK/BCI-代數(shù)，提出軟BCK/BCI-代數(shù)及其軟子代數(shù)和軟理想等概念。Khademan等在超BCK-代數(shù)中研究了模糊軟正關(guān)聯(lián)超BCK-理想。

交換BCK-代數(shù)是BCK-代數(shù)的重要子類，它可以構(gòu)成一個下半格。Iseki給出了交換BCK-代數(shù)的素理想的概念。素理想在交換BCK-代數(shù)結(jié)構(gòu)的研究中起重要作用。Jun等研究了交換BCK-代數(shù)的模糊素理想和可逆模糊理想。本文利用文獻(xiàn)[11]將參數(shù)集賦予代數(shù)結(jié)構(gòu)的思想方法，提出了交換BCK-代數(shù)的新型軟素理想的新概念，這與通常的交換BCK-代數(shù)的軟素理想不一樣，通常的軟集代數(shù)中，參數(shù)集可以沒有代數(shù)結(jié)構(gòu)，但初始集合必須有代數(shù)結(jié)構(gòu)，且參數(shù)的像必須是初始集合的子代數(shù)（理想等）。而本文定義的新型的軟集代數(shù)，是參數(shù)集必須有代數(shù)結(jié)構(gòu)，但初始集合可以沒有代數(shù)結(jié)構(gòu)，而且這種新型軟集代數(shù)比通常的軟集代數(shù)結(jié)果更深刻。

在已有的亞BCI-代數(shù)的新型軟理想的研究基礎(chǔ)上，進(jìn)一步研究了交換BCK-代數(shù)的新型軟理想的若干性質(zhì)。

1 預(yù)備知識

本章給出交換BCK-代數(shù)、軟集等下面要用的相關(guān)定義和定理。

一個（2,0）型代數(shù)(,*,0)是交換BCK-代數(shù)當(dāng)且僅當(dāng)下列等式成立：

（1）*=0

（2）*0=

（3）(*)*=(*)*

（4）*(*)=*(*)

設(shè)是交換BCK-代數(shù)，在中定義關(guān)系：*=0 ?≤，則(;≤)是一個偏序集。

是交換BCK-代數(shù)當(dāng)且僅當(dāng)(;≤)是一個下半格且對?,∈，有∧=*(*)。

（亞BCI-代數(shù)）一個(2,0)型代數(shù)(,*,0)如果滿足條件?,,∈，有：

（1）*0=

（2）*=0

（3）(*)*=(*)*

則稱為一個亞BCI-代數(shù)。

（軟集）設(shè)是一個初始集合，是參數(shù)集，?，()是的冪集，設(shè):→()為一個映射，則稱(,)是上的軟集，也稱為的軟集。

（新型軟理想）設(shè)是一個亞BCI-代數(shù)，:→()是一個軟集，若?,∈，滿足：

（1）(0)?()

（2）()?(*)?()

則稱是的一個新型軟理想，記為(,)。

（有界BCK-代數(shù)）若BCK-代數(shù)中的一個元素滿足?∈,有≤，則稱是有界BCK-代數(shù)。在有界BCK-代數(shù)中，把*記作N。

（兩個軟集的合成）設(shè)是亞BCI-代數(shù)，(,) 和(,) 分別為的兩個軟集。定義(?,)：

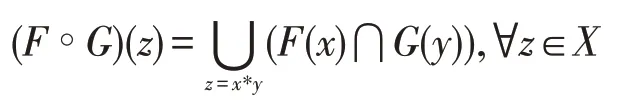
則(?,)是的軟集，并稱?為兩個軟集的合成。

（軟集的限制并）設(shè)(,)和(,)為上的軟集，若軟集(,?)滿足：

（1）?≠?；

（2）?∈?，有()=()?()。

則稱(,?)是軟集(,)和(,)的限制并，記作(,?)=(,)∪(,)。

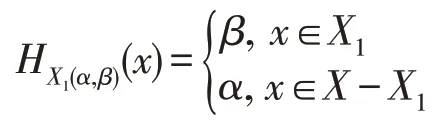
（關(guān)聯(lián)BCK-代數(shù)）設(shè)是BCK-代數(shù)，如果對?,∈，有*(*)=，則稱是關(guān)聯(lián)BCK-代數(shù)。

（素理想）設(shè)是交換BCK-代數(shù)，是的理想且滿足?,∈，若∧∈有∈或∈，則稱為的素理想。

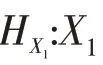
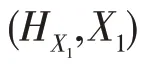
（對偶軟集）設(shè):→()，?()為一個軟集，則稱A:→()，?A()={|∈()}為的對偶軟集。設(shè):→()，?()為一個軟集，則稱H:→()，?H()={|∈()}為的對偶軟集。

設(shè)為亞BCI-代數(shù)，則下列結(jié)論成立：

（1）:→()為的新型軟理想的充要條件是?∈，A()≠?為的理想。

（2）:→()是一個軟集，則?∈，()≠?為的理想的充要條件是H為的新型軟理想。

設(shè)為亞BCI-代數(shù)，:→()為一個軟集，則是的新型軟理想的充要條件是的-水平集H={|()?,∈()}≠?為的理想。

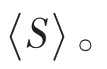
設(shè)是交換BCK-代數(shù)的理想，則下列條件等價：

（1）是素理想；

（2）對于的任意理想和，若??，則?或?；

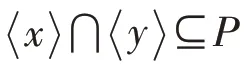
（像與原像）設(shè)、為兩個亞BCI-代數(shù)，是初始集合，()是的冪集，:→是一個映射，:→()，:→()均為軟集，?∈，∈，定義：

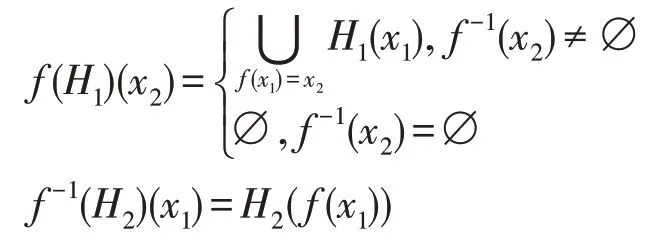
則()、()分別是和上的軟集，稱()為的像，()為的原像。

（同態(tài)與滿同態(tài)）設(shè)、是兩個亞BCI-代數(shù)，映射:→，若?,∈，有(*)=()*()，則稱為到的同態(tài)。當(dāng)是滿射時，則稱為到的滿同態(tài)。

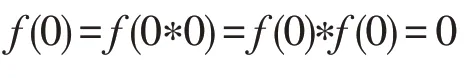
設(shè)、為兩個亞BCI-代數(shù)，是初始集合。:→為一個同態(tài)映射，:→()，:→()為兩個軟集，若為的新型軟理想，有()為的新型軟理想。

設(shè)、為兩個亞BCI-代數(shù)，:→為一個滿同態(tài)映射，:→()為軟集，則為的新型軟理想的充要條件是()為的新型軟理想。

（-不變性）設(shè)、為兩個集合，:→是到的映射，是上的軟集，?,∈，當(dāng)()=()時，有()=()，則稱是關(guān)于-不變的。

設(shè)、為兩個亞BCI-代數(shù)，是初始集合。:→為一個同態(tài)映射，:→()為軟集且是關(guān)于-不變的，若()為的新型軟理想，則為的新型軟理想。

設(shè)、為兩個亞BCI-代數(shù)，是初始集合。:→為一個滿同態(tài)映射，:→()為軟集且是關(guān)于-不變的,則為的新型軟理想的充要條件是()為的新型軟理想。

2 交換BCK-代數(shù)的新型軟理想

本章給出交換BCK-代數(shù)的新型軟理想與偏序之間的關(guān)系以及它在軟集運算下的性質(zhì)。

設(shè)是亞BCI-代數(shù)，?,∈，如果滿足*(*)=*(*)，則稱是一個交換亞BCI-代數(shù)。

注：由定理1 知，定義的交換亞BCI-代數(shù)就是交換BCK-代數(shù)。因此，下面主要討論交換BCK-代數(shù)的新型軟理想的性質(zhì)。

是交換BCK-代數(shù)，是的新型軟理想，若≤，則()?()。

若≤，則*=0，由是新型軟理想，得()?(*)?()=(0)?()=()。

設(shè)是交換BCK-代數(shù)的新型軟理想，且*≤，則()?()?() 。特別地，如果=0，則()?()。

因為*≤，由定理12 知，(*)?()。又是的新型軟理想，得()?(*)?()?()?()。特別地，若=0，則()?()?()=()?(0)=()。

設(shè)是有界BCK-代數(shù)，且是的新型軟理想，則()=()?(N)，?∈。

設(shè)是有界BCK-代數(shù)，且是的新型軟理想，則≤，有()?()；*≤，有(*)?()。因此()?()?(N)。又由是的新型軟理想，得()?(*)?()。

因此，()=()?(N)。

設(shè)是交換BCK-代數(shù)，是的一個軟集，如果?,∈,有(*)?()?()，則稱為的新型軟代數(shù)。

定理15是交換BCK-代數(shù)的新型軟理想，則是的新型軟代數(shù)。

?,∈，由是BCK-代數(shù)的新型軟理想，有(0)?()，且(*)?((*)*)?()=((*)*)?()=(0*)?()=(0)?()=()?()?()。

設(shè)是交換BCK-代數(shù)，若是的新型軟理想，則(,)=(,)。

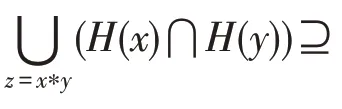
綜上所述，(,)=(,)。

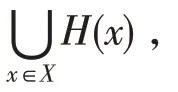
（1）設(shè)H是的軟集（=1,2），則(∪H)=()?()。

（2）設(shè)H是X的軟集（=1,2），則(∪H)?()?()。

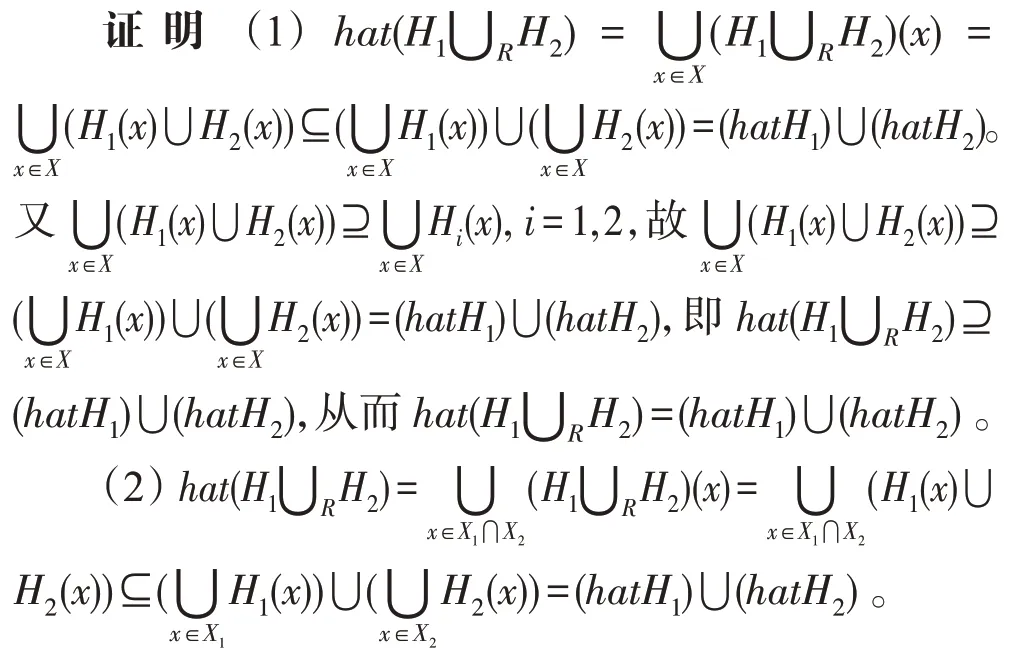
設(shè)是交換BCK-代數(shù)，(,)和(,)分別為的兩個軟集。定義(Δ,)：

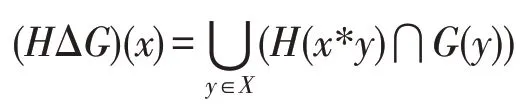
則(Δ,)是的軟集，并稱Δ為兩個軟集的合成。

是的新型軟理想的充要條件是Δ=且(0)=。

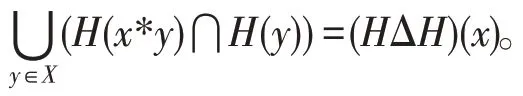
必要性：?∈，(0)=?()。

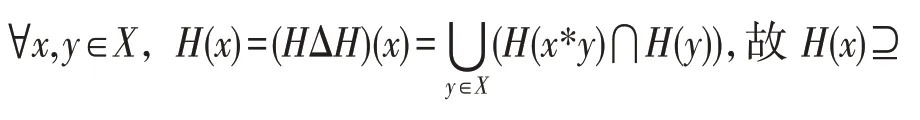
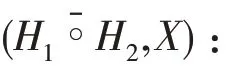
因?∈，有=∧，于是中的元素均有分解式=∧成立，所以上述定義是合理的。

設(shè)和是交換BCK-代數(shù)的兩個子代數(shù)，(,)和(,)分別為的兩個軟集。則：

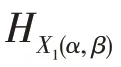
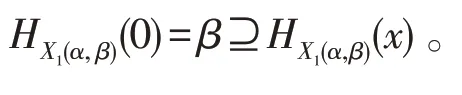
3 交換BCK-代數(shù)中軟集的零化子

本章給出了交換BCK-代數(shù)中軟集的零化子的新概念及相關(guān)性質(zhì)。

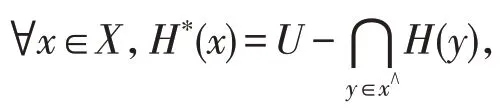
當(dāng)參數(shù)集固定時，兩個軟集的限制交（并）與擴(kuò)展交（并）重合，因此定理21就沒有區(qū)分。

設(shè)和是交換BCK-代數(shù)的兩個軟集，則有：

（1）(0)?()，?∈；

（2）如果≤，則()?()；

（3）如果?，則?；

（4）?，其中表示()；

（5）=；

（6）(?)??；

（7）(?)=?；

（8）???；

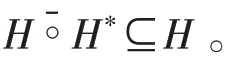
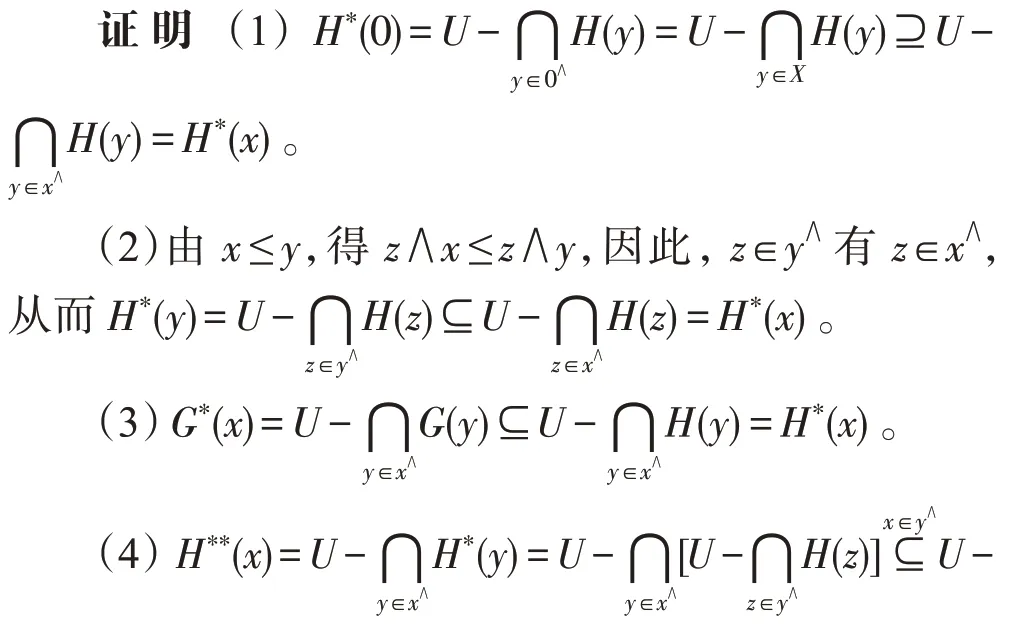
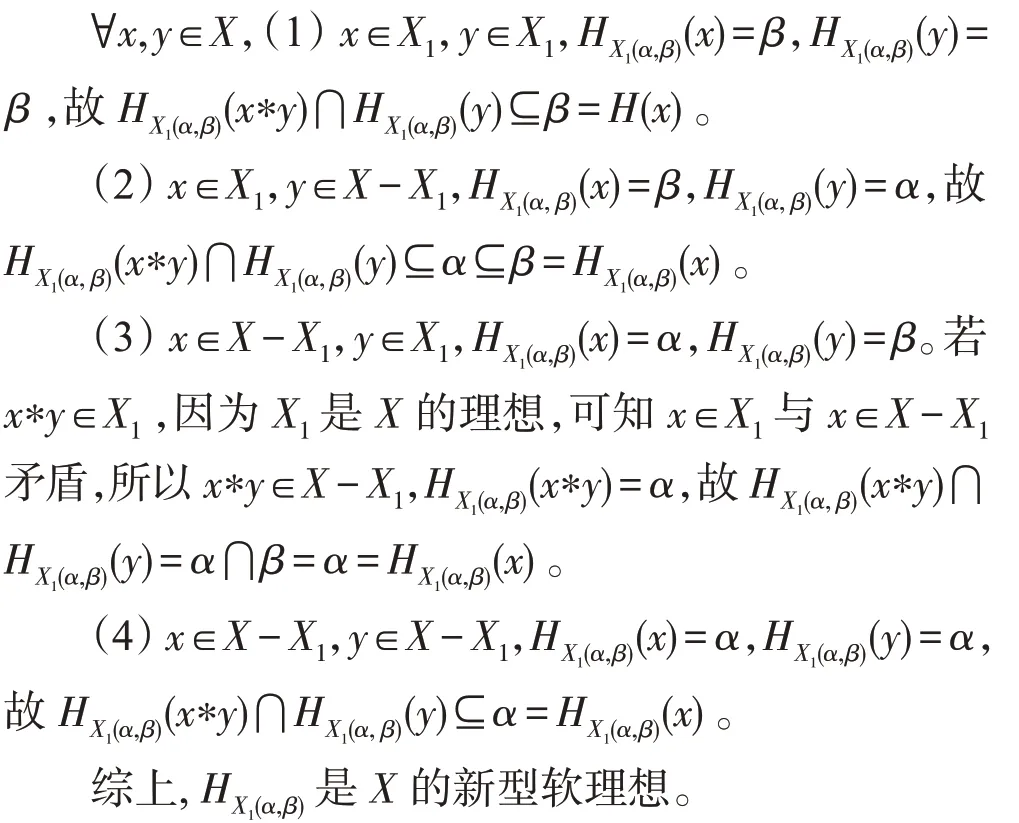
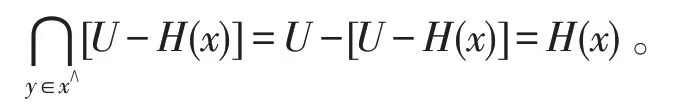
（5）在（4）中用替換得?，又?，由（3）得，?，因此=。

（6）因,??，由（3）得，(?)?且(?)?，所以(?)??。

（7）因??,，由（3）得，,?(?)，所以??(?)。又,??，由（3）得，(?)?,(?)?，所以，(?)????。由（3）和（4），得(?)?(?)??。綜上，(?)=?。

（8）和（9）由定理19可得。

設(shè)是交換BCK-代數(shù)的一個新型軟理想，如果=，則稱是的新型對合軟理想。

有界交換和關(guān)聯(lián)的BCK-代數(shù)的每個新型軟理想都是新型對合軟理想。

4 交換BCK-代數(shù)的新型軟素理想

本章給出了交換BCK-代數(shù)新型軟素理想的新概念和例子，研究了它在軟集運算下的性質(zhì)及等價刻畫。

設(shè)交換BCK-代數(shù)，是的一個軟集，如果滿足下列條件：

（1）是的新型軟理想；

（2）?,∈，有()?()?(∧)，則稱為的新型軟素理想。

是交換BCK-代數(shù)的新型軟素理想，則下列條件等價:

（1）?,∈，有()?()?(∧)；

（2）?,∈，有()?()=(∧)。

（1）?（2）由定理3，知∧≤,。由定理12知，(∧)?()且(∧)?()，因此(∧)?()?()，再由定義22知，(∧)=()?()。

（2）?（1）顯然成立。

由定理23知，下列定理成立。

是交換BCK-代數(shù)的新型軟素理想的充要條件是：

（1）是的新型軟理想；

（2）?,∈，有()?()=(∧)。

設(shè)有初始集合={,,,,}，參數(shù)集={0,1,2,3}，在上*運算定義如表1。

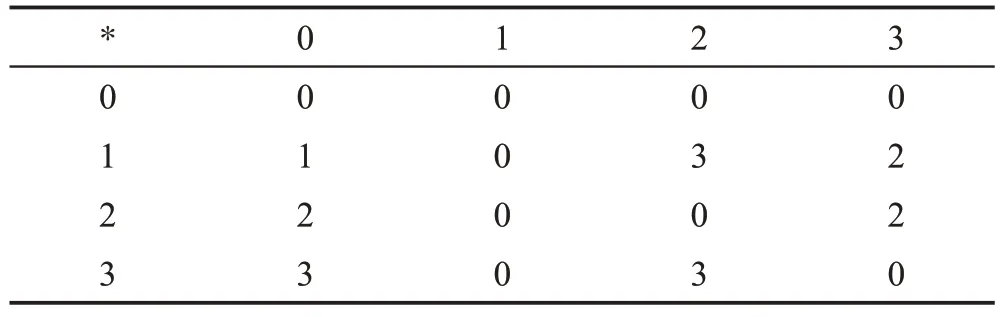
表1 運算“*”Table 1 Operator“*”

可驗證(,*,0)是一個交換BCK-代數(shù)。令:→()，(0)={,,,}，(1)={,}，(2)={,,}，(3)={,,}，由定義22 知，是的新型軟素理想,但它顯然不是通常的軟素理想。

設(shè)=={0,1,2,3},在上*運算定義如例1，令:→()，(0)={0,1,2,3}，(1)={3}，(2)={0,3}，(3)={1,2,3}，由定義知，是的新型軟素理想。因(1)={3}和(3)={1,2,3}不是的素理想，故它不是通常的交換BCK-代數(shù)的軟素理想，因此是一個新的軟代數(shù)結(jié)構(gòu)。

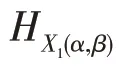
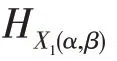
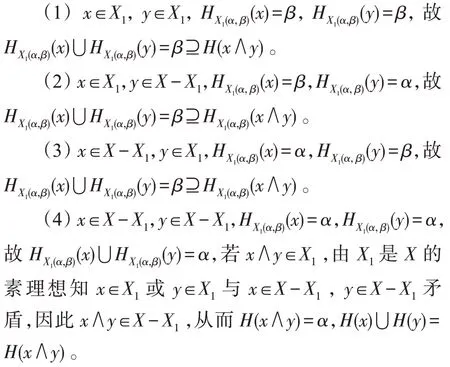
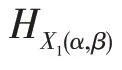
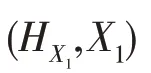
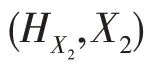
設(shè)是交換BCK-代數(shù)，則下列結(jié)論成立：

（1）:→()為的新型軟素理想的充要條件是?∈，A()≠?為的素理想。

（2）設(shè):→()為一個軟集，則?∈，A≠?為的素理想的充要條件是H為的新型軟素理想。

（1）必要性：由定義11和定理5得，A()≠?為的理想。?,∈，若∧∈A()，則∈(∧)。由是的新型軟素理想，得(∧)?()?()，因此∈()或∈()，有∈A()或∈A()。因此，A()為的素理想。

充分性：由定義9 和定理5 得，是的新型軟理想。?,∈，若(∧)=?，則顯然有(∧)?()?()；若(∧)≠?，則?∈(∧)，有∧∈A()，由A()為的素理想，得∈A()或∈A()，有∈()或∈()，因此∈()?()，故(∧)?()?()。因此，是的新型軟素理想。

（2）類似可證得。

設(shè)是一個交換BCK-代數(shù)，:→()為一個軟集，如果對?∈()，的-水平集H={|()?}≠?是的素理想，則是的新型軟素理想。

由定義9 和定理6 知，是的新型軟理想。?,∈，若(∧)=?，則顯然有(∧)?()?()；若(∧)≠?，令(∧)=，則∧∈H，由H≠?是的素理想，得∈H或∈H，因此()?或()?，有()?()?=(∧)。因此，是的新型軟素理想。

定理28的逆命題不成立，見例3。

可換BCK-代數(shù)(,*,0)和它的一個新型軟素理想同例2，取={0,1}，則有H={0}，而{0}不是的素理想，因為2×(2×3)=0，但2,3 ?{0}。

說明通常的模糊代數(shù)與軟集代數(shù)是有本質(zhì)區(qū)別的。

設(shè)是交換BCK-代數(shù)，是的一個軟集，下列條件等價：

（1）是的新型軟素理想；

（2）?∈，A()≠?是的理想，且對的任意理想和，由??A() 得?A() 或?A()；

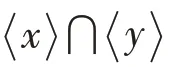
（1）?（2）由定理5 知當(dāng)A()≠?時，A()是的素理想，由定理7 知，?A()或?A()。（2）?（3）由定理7 知顯然成立。（3）?（1）由定理7 知A()≠?是的素理想，再由定理5 知是的新型軟素理想。

交換BCK-代數(shù)的一個新型軟理想稱為可逆的，如果它的軟零化子也是的新型軟理想。

交換BCK-代數(shù)的每個新型軟素理想是可逆的。

5 交換BCK-代數(shù)的新型軟素理想的像與原像

本章給出了交換BCK-代數(shù)的新型軟素理想的像與原像的性質(zhì)。

設(shè)、是兩個交換BCK-代數(shù)，是初始集合，:→()，:→()是兩個軟集，:→是到的映射。

（1）當(dāng)為一個同態(tài)映射時，為的新型軟素理想的必要條件是()為的新型軟素理想。

（2）當(dāng)為一個滿同態(tài)映射時，為的新型軟素理想的充要條件是()為的新型軟素理想。

（1）由定義22及定理8知，()為的新型軟理想。?,∈，令()=，()=∈，有()(∧)=((∧))=(()∧())=(∧)?()?()=(())?(())=()()?()()。因此，()為的新型軟素理想。

（2）必要性：由定理31（1）可知結(jié)論成立。充分性：由定義22 及定理9 知，為的新型軟理想。?,∈，由是滿同態(tài)映射，故?,∈，使得()=，()=，有(∧)=(()∧())=((∧))=()(∧)?()?()=()()?()()。因此，為的新型軟素理想。

設(shè)、是兩個交換BCK-代數(shù)，是初始集合，:→是到的映射，:→()為軟集且是關(guān)于-不變的。

（1）當(dāng)為一個同態(tài)映射時，()為的新型軟素理想的必要條件是為的新型軟素理想。

（2）當(dāng)為一個滿同態(tài)映射時，()為的新型軟素理想的充要條件是為的新型軟素理想。

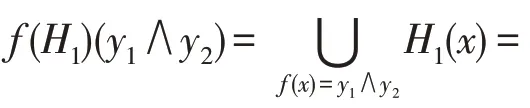
6 結(jié)束語

本文提出并研究了交換BCK-代數(shù)的新型軟（素）理想，獲得了一系列的結(jié)果。其中，引進(jìn)軟集的新的運算及偏序關(guān)系對交換BCK-代數(shù)的新型軟（素）理想進(jìn)行刻畫，是本文的特色。今后將進(jìn)一步利用本文的思想和方法研究亞BCI-代數(shù)的其他理想。