混合優化算法求解同時送取貨車輛路徑問題

李 珺，段鈺蓉，郝麗艷，張維維

蘭州交通大學 電子與信息工程學院，蘭州730070

近年來，為了避免環境污染，很多國家制定了相應的法律法規，要求企業對整個產品的生命周期負責，不僅要提供客戶滿意的配送服務，還要進行廢棄物的回收利用。因此，企業有了構建正向物流配送和逆向廢舊物品回收相結合的物流系統的迫切需求；而客戶往往只在特定的時間窗內接受服務。為了提升服務質量和客戶滿意度，企業不僅需要完成同時送取貨的作業，還要額外考慮客戶的服務時間窗。因此，如何設計出合理完善的帶時間窗的雙向物流系統，成為理論研究和實踐中關注的重要問題。在運籌學領域，該類問題被稱為帶時間窗和同時送取貨的車輛路徑問題（vehicle routing problem with simultaneous delivery-pickup and time windows，VRPSDPTW）。

VRPSDPTW 問題作為車輛路徑問題（vehicle routing problem，VRP）的重要擴展，屬于NP-hard 問題。這類問題的解決方法主要分為精確算法和啟發式算法。2002年，Angelelli等最早提出VRPSDPTW問題，使用精確算法中的分支-價格法求解算例規模為20 個客戶點的小型算例。當客戶規模增大時，精確算法不能在合理的時間范圍內求得滿意解。學者們開始嘗試設計不同的啟發式算法來解決VRPSDPTW問題。Cao等提出了一種改進的遺傳算法，根據用戶的優先順序重新設計了編碼方式。當最大客戶數目為8時，改進算法能有效找到最優解，然而，在現實生活中，客戶數目遠遠多于8個。Boubahri等設計了一個多智能體群體系統來解決VRPSDPTW問題。盡管這種解決方法很新穎，但是作者沒有提供任何數值實驗結果。2012年，Wang等采用協同進化遺傳算法解決VRPSDPTW問題，并在經典的Solomon數據集的基礎上設計了VRPSDPTW基準實例，實驗結果表明，所提出的協同進化遺傳算法能夠在較短的時間內找到滿意解。王超等運用回溯搜索優化算法來求解該問題，選取了測試數據集中的6個算例進行了實驗。王超等提出了一種離散布谷鳥算法來求解該問題。除此之外，還有改進全局人工魚群算法、大鄰域搜索算法等。

目前關于VRPSDPTW 問題，雖然學者們已經進行了一些研究，但是仍然缺乏有效的求解方法。迄今為止，VRPSDPTW問題的解決，主要采用啟發式算法，并且以Wang等設計的測試數據集作為國際通用數據集，各類文獻中的已知算法在對算例進行測試時，都無法找到所有算例的最優解，因此，高效、穩定的求解方法成為學者們追求的目標。

為了更好地解決VRPSDPTW 問題，通過大量的實驗發現，模擬退火算法（simulated annealing，SA）在依據概率突跳特性進行降溫尋優的過程中，對較差的解具有一定的容忍性，使得算法的全局尋優能力優于很多當前流行的智能優化算法，同時能夠在一定程度上克服對初始解的依賴性；自適應大規模鄰域搜索算法（adaptive large-scale neighborhood search，ALNS）能夠較好地避免算法在尋優過程中陷入局部極值，且在鄰域搜索的過程中，通過一些啟發式信息來指導尋優，能夠在一定概率上獲得高質量的解。將模擬退火和大規模鄰域搜索算法相結合，本文提出一種混合優化算法（SA-ALNS），以標準模擬退火算法作為主體，用插入啟發式算法構造問題的初始解，結合自適應大規模鄰域搜索算法進行尋優。實驗結果表明，本文所提出SA-ALNS 有效縮短了物流配送路徑長度，節約配送成本，為各企業解決VRPSDPTW問題提供有效的解決方案。

1 VRPSDPTW問題

1.1 問題描述

VRPSDPTW 問題可以描述為：一個配送中心擁有若干型號相同且載重能力相同的車輛，為分布在不同位置的已知客戶提供送貨、取貨服務。每一個客戶的地理位置信息已知、送貨量和取貨量已知、服務時間窗以及持續服務時間已知。要求配送中心在滿足客戶需求的基礎上規劃出合理的配送路線，最小化總配送成本，并滿足以下假設：

（1）每個客戶只能由一輛車完成送貨和取貨服務，且需求不可拆分；

（2）每輛車均從配送中心出發，在送取貨任務完成后返回配送中心；

（3）每輛車的載貨量不能超過車輛載重；

（4）在客戶規定的服務時間窗內，先進行送貨服務，再進行取貨服務；

（5）每一條道路都暢通，不考慮道路突發狀況。

1.2 符號定義

為了方便構造VRPSDPTW 數學模型，需要對所用到的符號進行說明：

（1）參數

表示需要服務的客戶集合和配送中心；N表示需要服務的客戶集合，∈{1,2,…,} ；表示配送中心；表示車輛集合，={1,2,…,}；D表示每個客戶的送貨量；P表示每個客戶的取貨量；D表示客戶到客戶的歐氏距離(,∈)；[ET,LT]表示客戶的服務時間窗，其中ET為客戶允許的最早開始服務的時間，LT為客戶的最晚開始服務時間；S表示客戶所需的持續服務時間；表示車輛的最大載重量。

（2）決策變量

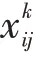
（3）衍生變量

St表示客戶的開始服務時間；T表示從客戶到客戶所花費的時間；表示車輛從配送中心出發時的裝載量；p表示車輛在離開客戶時的裝載量，∈{1,2,…,}。

1.3 VRPSDPTW數學模型

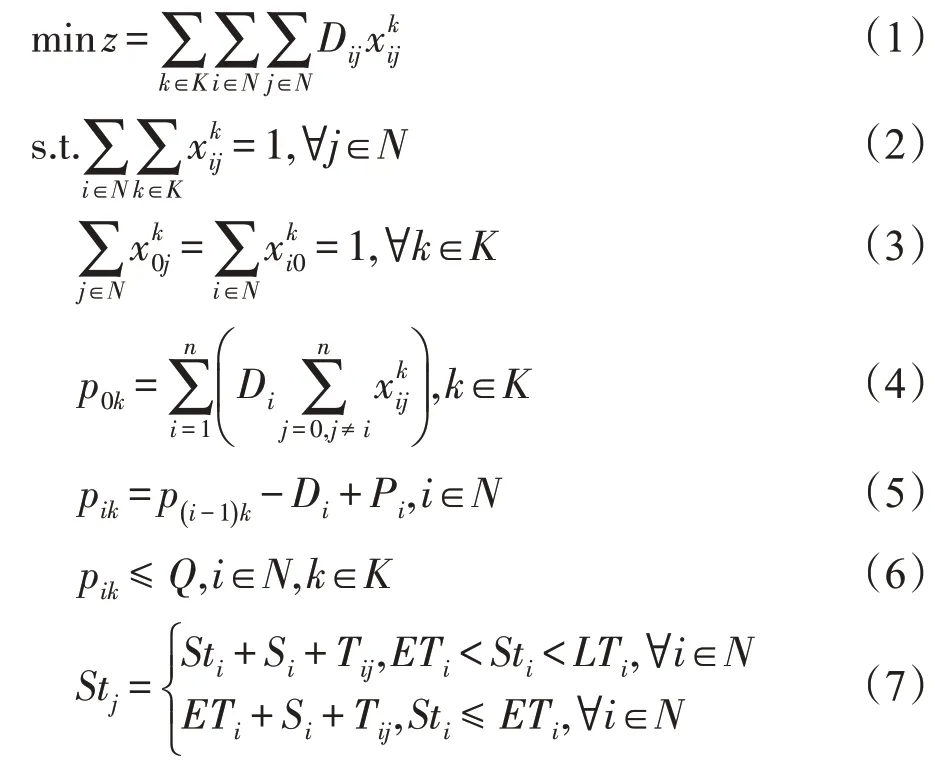
其中，式（1）為目標函數，表示最小化車輛總距離；約束（2）表示每個客戶都只能由一輛車服務；約束（3）保證所有車輛從配送中心出發最終返回配送中心；約束（4）表示車輛在離開配送中心時的裝載量即某條路徑上所有客戶的送貨量總和；約束（5）表示車輛在離開每個客戶時的裝載量，即離開上一個客戶時的裝載量減去本客戶的收貨量（車輛的送貨量），再加上本客戶的寄貨量（車輛的取貨量）；約束（6）保證車輛在任何時刻的裝載量都不超過車輛的最大載重量；約束（7）表示滿足客戶的服務時間窗要求。

2 VRPSDPTW問題的混合優化算法設計

混合優化算法（SA-ALNS）在SA 的基礎上結合ALNS 思想進行尋優。SA-ALNS 中設計了多個插入、刪除算子，且為每個算子賦予分數和權重，在鄰域搜索的過程中根據各個算子的分數和權重動態選取插入算子和刪除算子對現有解進行重構，從而得到質量更好的解。由于ALNS 的接受準則和停止準則一般是根據目標值來判斷，這種方法存在準確性差、魯棒性弱的缺點，引入SA 中的退火準則來控制解的更新，提高解的質量。

2.1 編碼方式

算法采用整數編碼，編號0 表示配送中心，編號1,2,…,表示客戶點。令=[[1],[2],…,[]]，為負責服務客戶的車輛順序排列的組合。假設為客戶服務的車輛規劃路徑如圖1 所示，則=[[1],[2]]=[0 7 2 3 9 1 0 0 6 5 8 4 0]。從圖1 可以看出，共有9 個需要服務的客戶，配送中心一共啟用了2 輛車，第一輛車從配送中心出發，分別為客戶7、客戶2、客戶3、客戶9、客戶1 提供送取貨服務，最后返回配送中心；第二輛車從配送中心出發，服務客戶6、5、8、4 后，返回配送中心。

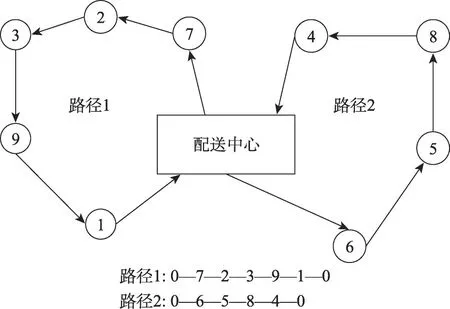
圖1 車輛規劃路徑Fig. 1 Vehicle planning route

2.2 初始解構造

采用插入啟發式算法構造VRPSDPTW 問題的初始解。用插入法構造初始解時，由于客戶有服務時間窗約束，故采用Solomon的基于距離與時間加權的插入標準。

式中，為待插入客戶點；d表示客戶到客戶的距離；(,,)表示客戶插入、兩點間后，路徑距離的增量。

式中，St表示將客戶插入客戶、之間后，客戶的新開始服務時間；St為客戶的原開始服務時間；(,,)表示客戶插入路徑后對客戶的開始服務時間的影響。

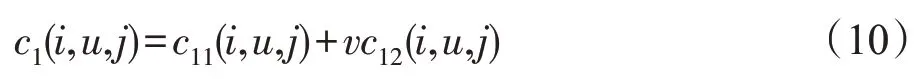
式中，為車輛當前行駛速度，(,,)表示客戶插入路徑后，對路徑產生的影響。在配送過程中，為了同時考慮路徑增加部分和服務時間增加部分對整體配送過程的影響，引入了車輛行駛當前速度值，通過當前速度與增加服務時間的乘積，將時間量轉化為路程量，使得衡量的標準統一為距離，方便計算；考慮到車輛在配送過程中可能會出現交通擁堵的情況，車輛的行駛速度會發生變化，式（10）在速度動態變化的情況下能更精確地反映待插入客戶對整個路徑的影響程度，為求解多通路車輛路徑問題提供一種思路。

式中，(,,)表示插入標準值。通過(,,)篩選出距客戶和客戶越近且距離配送中心越遠的客戶點，優先插入路徑中，從而提高后期優化階段中SAALNS算法的收斂速度。計算中，引入常數≥1，對進行放大，提高插入標準值的敏感性。

基于距離與時間加權的插入法，過程如下：

（1）生成一條只包含車輛起點和終點的初始路徑[0 0]；

（2）在所有的客戶點中隨機選擇一個客戶點作為種子節點插入初始路徑中；

（3）計算剩余客戶點在所有可能插入位置的插入標準值；

（4）將插入標準值降序排列，把插入標準值最大的客戶點插入到最佳可行的位置，若路徑中客戶總送貨量超過車輛的最大載重量，則重新生成一條路徑；

（5）重復步驟（3）、（4），直到所有的客戶都插入路徑。

2.3 路徑優化

在尋優階段，引入刪除算子、插入算子和自適應選擇策略進行路徑優化。刪除算子按照一定的規則從路徑中刪除部分客戶點，插入算子將刪除的客戶點重新添加到路徑中的合理位置，得到新解。根據各個刪除、插入算子在程序運行中的表現，自適應調整權重，不斷地更新算子的選中概率，以不同的方式完成刪除和插入操作，提高解的多樣性，從而更好地進行全局尋優。

選用四種刪除算子，通過不同的方式隨機在路徑中選擇客戶點，將其在路徑中刪除，為局部尋優做準備。

（1）Random removal算子

該算子從客戶集合中隨機選取個客戶，將個客戶從相應的路徑中移除，以增加搜索的多樣性。

（2）Random schedule removal算子

該算子會隨機選擇一條路徑，將這條路徑上的所有客戶刪除，為這些客戶重新尋找配送位置。這種方式在一定概率上能夠減少車輛的使用數量，從而降低物流成本。

（3）Worst removal算子

算子的主要目的是最小化總行駛距離。從客戶集合中選取一個客戶點，計算并保存該點被刪除前后路徑距離的節約值，剩余的客戶點重復此過程，從而得到全部客戶點被刪除前后路徑距離的節約值，將所有客戶點距離的節約值降序排序，選取前個節約值較大的客戶點從相應的路徑中刪除。

（4）Node distance removal算子

該刪除算子首先計算每條路徑的平均距離占用值，然后將平均距離占用值最大的路徑中的客戶點全部刪除。平均距離占用值的計算公式為：

式中，()表示第條路徑的總距離，N表示第條路徑中的客戶數量。根據平均距離占用公式，選擇一條最不經濟的路徑刪除其中所有客戶點。

文中選用兩種插入算子，使用不同的插入規則將刪除的客戶點重新插入到路徑中。

（1）Greedy insertion算子

該方法隨機選取一個待插入客戶點，遍歷每條路徑，找到所有既滿足時間窗約束又不超過車輛最大載重量的可插入位置，計算該客戶點插入到每個可插入位置前后的距離增量，選擇距離增量最小的位置將客戶點插入。若遍歷所有路徑都沒有找到符合時間窗和車輛載重約束的可插入位置，就重新生成一條初始路徑，將客戶點添加到其中。重復上述過程，直到將所有的待插入客戶點添加到路徑中。

（2）Regret insertion算子

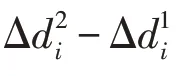
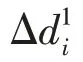
混合算法以模擬退火算法的基本結構進行尋優，尋優過程中，以自適應方式選擇刪除和插入算子。

每一個溫度下（以下簡稱為階段），算法進行次尋優迭代；每次迭代時，SA-ALNS采用輪盤賭機制選擇一個刪除和一個插入算子完成路徑的更新；之后根據新得到的路徑的優劣，對所選用的刪除、插入算子評分。所得分數將影響下一階段中該算子的權重，得分越高的算子在下一階段輪盤賭選擇策略中的權重值將越大，被選中的概率越高。算子第階段的得分，計算公式如式（14）。

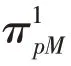
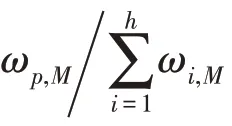
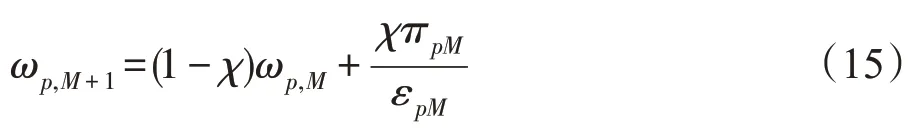
其中，π表示算子在第個階段所得分數；ε表示算子在第階段被選擇的次數；常數∈[0,1]，本文取的值為0.1。每個算子的權重與該算子所得分數、選擇次數有關，分數越高，權重越大，選擇概率就越大。算子的權重作為一種啟發式信息，使算法偏向于選擇效果好的算子，從而在很大概率上能夠獲得更滿意的解。

2.4 可行解的接受條件和迭代結束標準

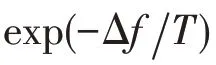
2.5 混合優化算法流程

初始化基本參數：初始溫度，每個溫度下的最大迭代次數，結束溫度。采用插入啟發式算法構造初始解。

用輪盤賭機制分別選擇一種刪除算子和插入算子，生成一個新解。

計算的目標函數值，根據Metropolis準則更新當前解，并更新各個算子的分數。

若達到每個溫度下的最大迭代次數，則更新刪除、插入算子的權重并執行降溫=操作，其中，為降溫速率。

若達到足夠低的溫度(＜)，輸出最優解，整個算法結束；否則回到步驟2。

混合優化算法的流程圖如圖2所示。

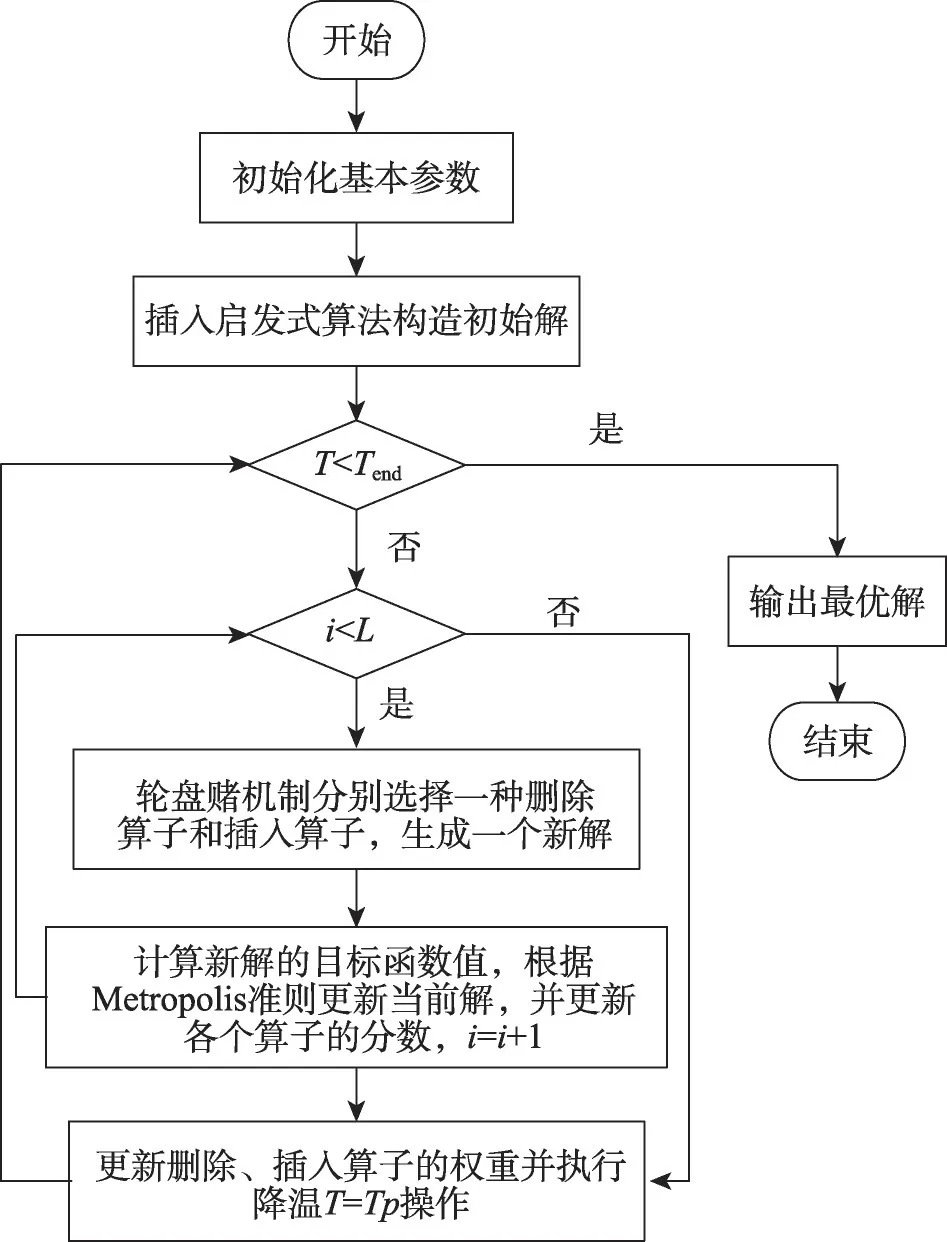
圖2 混合算法流程Fig. 2 Hybrid algorithm flow

3 實驗與分析

程序使用Matlab（R2016a）編寫，并在IntelCorei5-7300HQ CPU@2.50 GHz處理器，8 GB內存和16位操作系統的Windows10計算機上進行。

為了驗證SA-ALNS 算法的性能，選取Wang 等設計的求解VRPSDPTW 的測試算例（數據集網址http://oz.nthu.edu.tw/～d933810/test.htm）。共56 個大規模算例，可分為Rdp1、Rdp2、Cdp1、Cdp2、RCdp1、RCdp2，共6 類。Rdp1 類和Rdp2 類中的客戶地理位置滿足隨機分布，較為分散；算例Cdp1、Cdp2中的客戶位置滿足聚類分布，相對較聚集；RCdp1 類和RCdp2 類客戶地理位置通過聚類分布和隨機分布混合生成，部分聚集，部分分散。此外，Rdp1、Cdp1、RCdp1 算例集具有較緊的時間窗，較小的車輛裝載量；而Rdp2、Cdp2、RCdp2算例集的時間窗較寬，車輛裝載量較大。

SA-ALNS算法在每個算例上運行10次，并記錄最優值。本文提出的SA-ALNS 算法與文獻[6]中的DCS 算法、文獻[11]中的p-SA 算法、文獻[12]中的ETSP算法、文獻[13]中的ALNS-PR算法、文獻[14]中的VNS-BSTS 算法以及文獻[15]中的Par-SAA 算法進行對比。SA-ALNS 算法在Cdp1 類、Cdp2 類算例上與其他算法最優值的對比結果如表1 所示，在Rdp1 類、Rdp2 類算例上的對比結果如表2 所示，在RCdp1類、RCdp2類算例上的對比結果如表3所示。

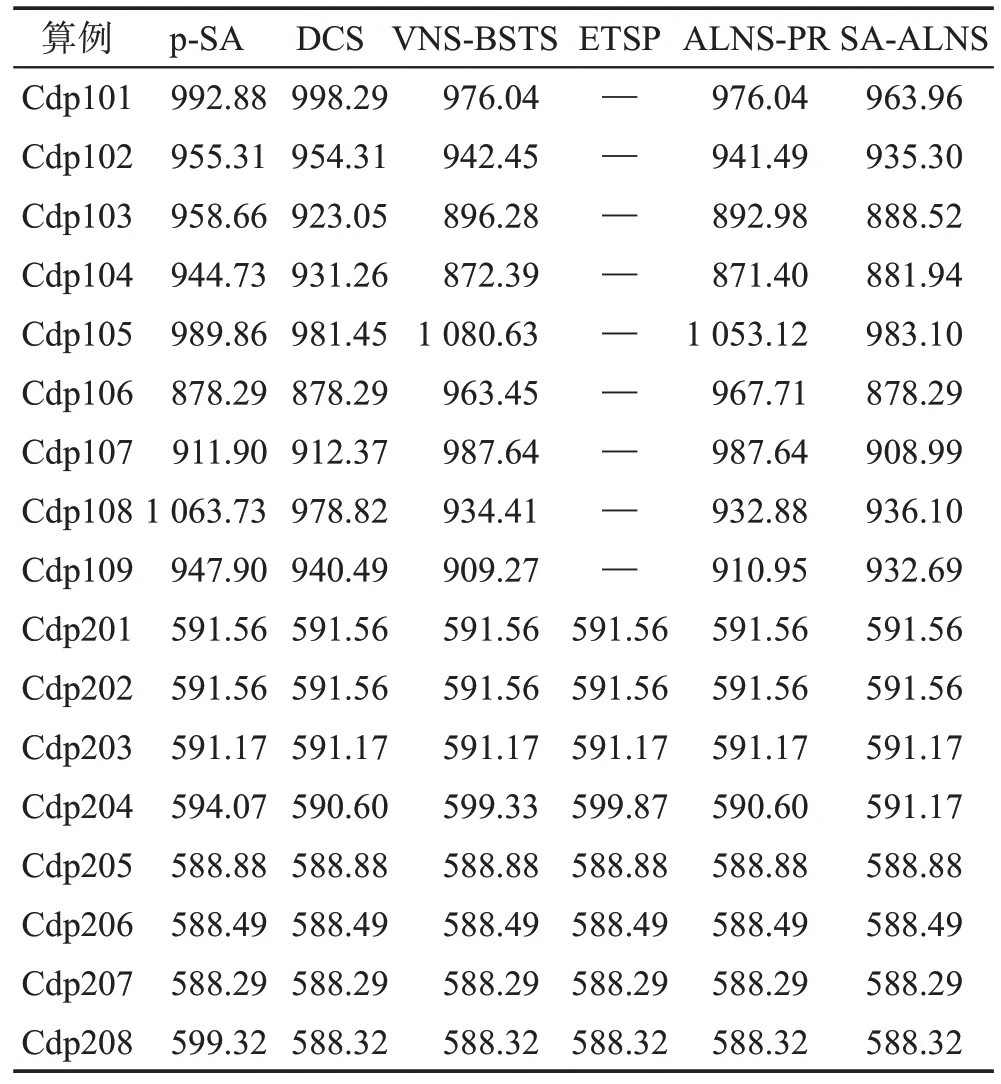
表1 SA-ALNS在Cdp類算例與其他算法的最優值對比Table 1 Best value comparison between SA-ALNS and other algorithms in Cdp examples

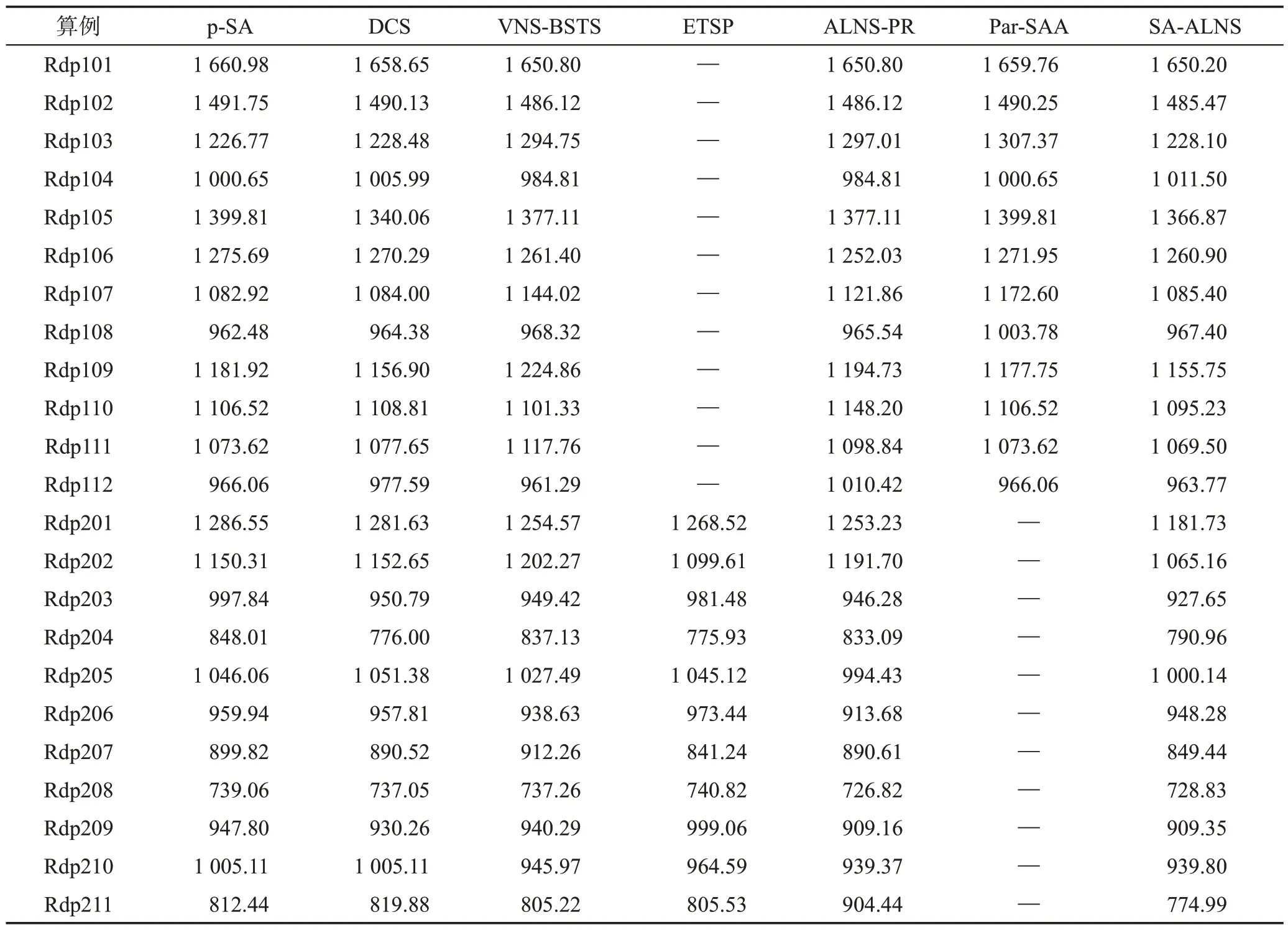
表2 SA-ALNS在Rdp類算例與其他算法的最優值對比Table 2 Best value comparison between SA-ALNS and other algorithms in Rdp examples

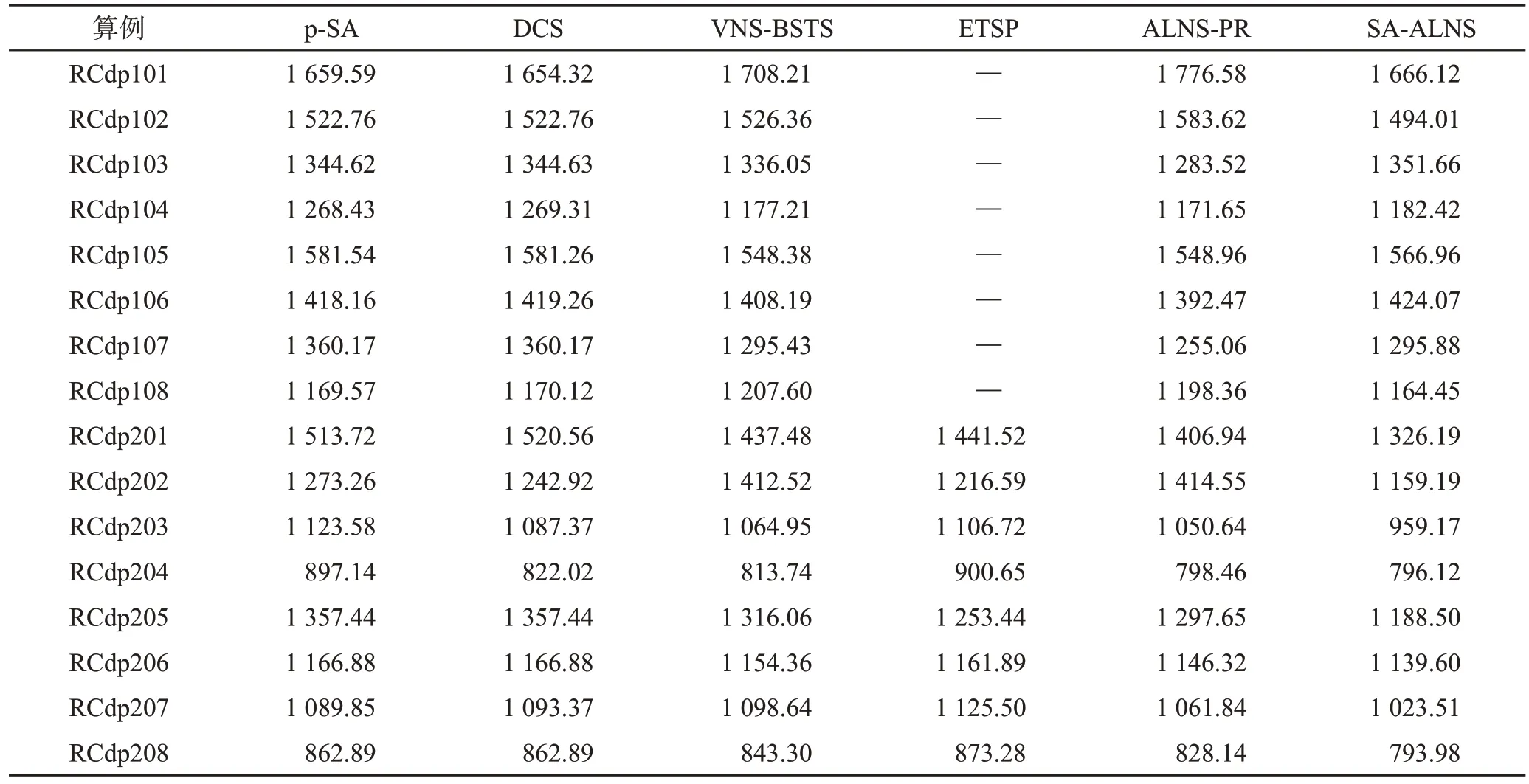
表3 SA-ALNS在RCdp類算例與其他算法的最優值對比Table 3 Best value comparison between SA-ALNS and other algorithms in RCdp examples

混合優化算法的參數設置：初始溫度設為500，截止溫度為0.001，降溫速率為0.95，最大迭代次數設為100。

對Cdp1 類、Cdp2 類算例進行測試，SA-ALNS 算法在每個算例上的最好結果見表1。從表中可以看出，在Cdp104、Cdp108、Cdp109 算例中，SA-ALNS 算法的實驗結果比VNS-BSTS、ALNS-PR的結果差；在Cdp105 算例中，SA-ALNS 的尋優效果弱于DCS 算法；在Cdp204算例上，DCS、ALNS-PR算法的實驗結果優于SA-ALNS；在除Cdp204 的其他Cdp2 類算例中，SA-ALNS算法均獲得了最優解；本文算法在Cdp1類和Cdp2 類算例上都優于p-SA 算法。總的來說，SA-ALNS算法的計算精度較高。

由表2 可看出，與p-SA 算法相比，在Rdp103、Rdp104、Rdp107、Rdp108算例上，SA-ALNS的求解性能弱于p-SA，在其余算例上的求解性能均優于p-SA；

同DCS 算法相比較，SA-ALNS 在Rdp104、Rdp105、Rdp107、Rdp108、Rdp204算例上的效果弱于DCS，其余算例的效果優于DCS；與VNS-BSTS 算法相比較，在Rdp104、Rdp112、Rdp206 算例上，SA-ALNS 的實驗結果較差，但在其他算例上都領先于VNS-BSTS；同ETSP 相比，SA-ALNS 在除Rdp204、Rdp207 之外的其他算例上都獲得最優解；同ALNS-PR相比，SAALNS 在Rdp104、Rdp106、Rdp108、Rdp205、Rdp206、Rdp208、Rdp209、Rdp210 算例上的求解性能弱于ALNS-PR，但在其余算例上求解性能強于ALNS-PR；與Par-SAA算法相比，SA-ALNS在除Rdp104的其他算例上均優于Par-SAA。在Rdp1、Rdp2 類算例中，SA-ALNS 在82.6%算例上優于p-SA，在78.2%算例上優于DCS，在87.0%算例上優于VNS-BSTS，在81.8%算例上優于ETSP，在65.2%算例上優于ALNSPR，在91.7%算例上優于Par-SAA。

實驗結果分析：由表3 可以看出，在RCdp1 類算例中，SA-ALNS在求解RCdp101、RCdp103、RCdp106算例時，尋優結果弱于p-SA和DCS，但在其余算例的尋優結果都強于p-SA、DCS；SA-ALNS在求解RCdp103、RCdp104、RCdp105、RCdp106、RCdp107時，求解能力比VNS-BSTS、ALNS-PR 弱。在RCdp2 類算例，SAALNS算法的運行結果均優于對比算法。

從Cdp1、Cdp2、Rdp1、Rdp2、RCdp1、RCdp2 算例的實驗結果可以看出，本文所提出的SA-ALNS 在求解VRPSDPTW問題中有不錯的效果，說明該方法是行之有效的。

圖3是SA-ALNS與其他的算法分別在Cdp1類、Cdp2 類、Rdp1 類、Rdp2 類、RCdp1 類、RCdp2 類算例上的實驗結果對比，能夠更加清晰地看出不同算法求得的最短距離值之間的差距。

圖3 不同算法在不同算例上的對比Fig. 3 Comparison of different algorithms on different examples

部分算例的路徑優化圖，如圖4。

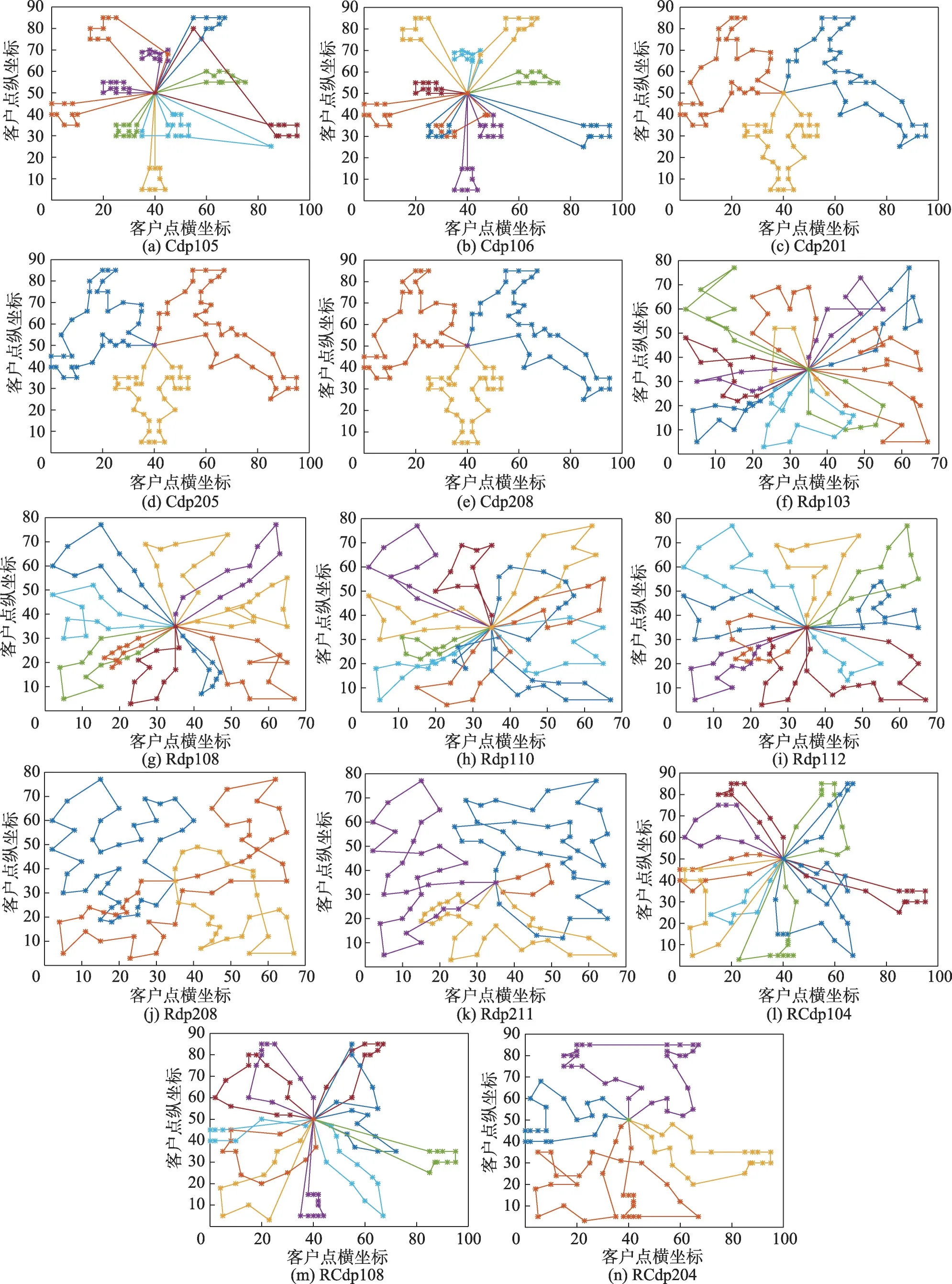
圖4 部分算例的路徑優化圖Fig. 4 Path optimization graph of some examples

4 結束語

本文針對VRPSDPTW問題提出了一種SA-ALNS算法，該算法運用插入啟發式算法構造初始解，以模擬退火為框架，采用自適應大規模鄰域搜索算法進行鄰域搜索，并設計了四種刪除算子和兩種插入算子，增大鄰域搜索的范圍，從而加速解的收斂。通過Cdp1類、Cdp2類、Rdp1類、Rdp2類、RCdp1類、RCdp2類算例測試，并與其他已知算法對比，最后證明了SA-ALNS 算法的優越性和有效性。現如今，人們越來越關注環境保護問題，綠色物流將是未來物流行業的發展趨勢，在車輛路徑問題中考慮碳排放等約束條件，從而衍生出更多復雜的VRP問題，本文所提出的SA-ALNS 為解決這些復雜VRP 問題提供一種新思路。