混沌反饋共享和群體協同效應的蝴蝶優化算法

李守玉，何 慶＋，杜逆索

1.貴州大學大數據與信息工程學院，貴陽550025

2.貴州大學貴州省大數據產業發展應用研究院，貴陽550025

為了更好解決現實中的復雜優化問題，研究者們通過觀察、研究自然界中生物的生理或物理現象，提出了粒子群優化算法、灰狼優化算法、樽海鞘優化算法、飛蛾撲火算法及蝴蝶優化算法等元啟發式算法，并將它們用于解決現實中的工程優化任務。

傳統的粒子群算法雖收斂速度快、易于實現，但存在早熟現象，蟻群算法雖有較強的記憶性，但它容易出現停滯現象且效率低。蝴蝶優化算法（butterfly optimization algorithm，BOA）是由Arora和Singh 于2019 年提出的基于全局優化的群智能算法。BOA通過蝴蝶之間散發的香味形成一個具有一定信息損失的一般社會交互網絡，其具有原理簡單、參數少、計算耗時少及易于實現等優點，因此被應用于陰影光伏陣列的重構技能的工程設計、優化無線傳感器網絡的能量有效簇、小波神經網絡的訓練、家庭CO減排策略混合智能預測模型及認知智能電網中基于能效優化的頻譜分配策略等領域。

然而蝴蝶優化算法也存在收斂速度慢及尋優精度不高的缺陷。為此，研究者提出了不同的改進策略。文獻[9]通過將柯西變異和自適應權重結合增強算法跳出局部最優的能力和全局搜索的能力，使用動態切換概率調節全局與局部搜索的比重。文獻[10]利用混沌理論與正余弦算法結合的方式增強算法的尋優能力，使用線性遞減控制香味的冪指數提高收斂精度。文獻[11]通過交叉熵和協同進化技術找尋全局與局部搜索之間平衡，提高算法的全局搜索能力。文獻[12]利用limit 閾值克服陷入局部的難題，再將單純形法和正弦余弦指引策略結合對位置進行更新，提高算法的尋優性能。文獻[13]利用擾動策略和瘋狂因子增加算法的多樣性，通過線性遞減慣性權重平衡全局與局部搜索的能力。盡管改進算法尋優精度有所提升，但收斂速度和穩定性仍有很大改進空間。

針對蝴蝶優化算法存在的問題，本文提出了混沌反饋共享和群體協同效應的蝴蝶優化算法（butterfly optimization algorithm based on chaotic feedback sharing and group synergy，CFSBOA）。算法利用二維的Hénon映射，使得種群個體的搜索分布更加均勻，增加算法多樣性；通過正反饋或負反饋網絡加快算法的信息流動，進而增強逃離局部最優的能力；最后融合群體協同，進一步矯正和協調種群的進化方向及更好地平衡全局與局部搜索能力。通過求解12個基準測試函數和部分CEC2014測試函數驗證算法的有效性和魯棒性。

1 蝴蝶優化算法

在標準BOA 算法中，蝴蝶種群采用隨機初始化蝴蝶種群：

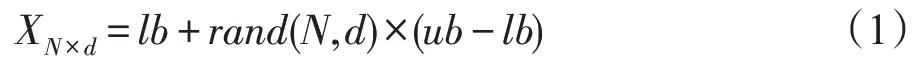
式中，表示蝴蝶種群規模，表示搜索空間維度。

蝴蝶算法假定搜索空間中的每個個體能感知彼此散發的香味；蝴蝶能根據香味濃度的強弱進行隨機移動或向最好蝴蝶移動；蝴蝶的感覺模態受目標函數的范圍影響或決定。由于蝴蝶進行食物源搜索時，香味大小受風、雨、溫度等因素影響和限制，采用轉換概率控制蝴蝶的搜索模式：全局搜索或局部搜索。

蝴蝶香味計算公式：

其中，代表香味大小；是感官模態強度；是刺激強度；是依賴感官模態的冪指數；表示最大迭代次數。

蝴蝶的位置更新由局部搜索和全局搜索構成。若蝴蝶因距離和自然因素無法感知到其他蝴蝶散發的香味，則蝴蝶在局部執行隨機搜索；若蝴蝶能夠感知到其他蝴蝶散發的香味，它能根據香味強弱，飛向最好蝴蝶實現蝴蝶位置更新，從而使得種群向食物源位置進行搜索。

當≥時，進行局部搜索：

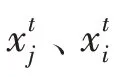
當＜時，進行全局搜索：

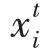
2 混沌共享反饋和群體協同效應的蝴蝶優化算法

2.1 Hénon初始化機制

標準BOA利用式（1）隨機初始化蝴蝶位置，可能會出現蝴蝶位置在搜索空間中分布不均勻，導致算法過早陷入局部最優，出現早熟現象。文獻[14]利用Tent映射初始化樽海鞘種群，使得樽海鞘個體均勻分布在搜索空間上，從而提高算法尋優精度。

混沌映射具有遍歷性、隨機性和規律性等優點，其基本思想利用映射關系產生[0,1]的混沌序列，再將混沌序列轉化到個體的搜索空間。常用來初始化種群的混沌映射有Tent映射、Logistic映射，但文獻[15]指出Tent 映射存在小周期和不穩定周期容易使Tent映射易陷入不動點；Logistic 映射在[0,1]范圍內呈切比雪夫分布，搜索盲區大。然而Hénon 不僅能克服Tent映射和Logistic映射的缺點，其產生的混度序列也更加均勻，如圖1所示。利用Hénon的混沌序列分布更加均勻的特點，種群可以最大程度覆蓋搜索盲區，增加蝴蝶個體的多樣性，從一定程度上幫助算法跳出局部極值，進而增強算法尋優的能力。因此，本文采用Hénon混沌映射初始化蝴蝶種群。其數學描述：

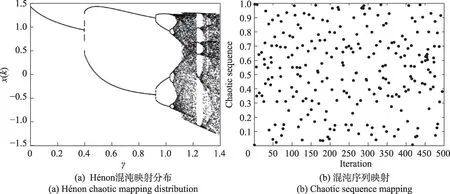
圖1 Hénon混沌映射Fig. 1 Hénon chaotic mapping

2.2 反饋共享機制

由于標準BOA算法只通過全局最優解的位置進行信息交流，很大程度上限制蝴蝶的搜索范圍，增大算法陷入局部最優的風險，降低算法的尋優精度。為了增強算法跳出局部最優的能力，參考電路分析中反饋控制電路的概念，讓蝴蝶受到其他蝴蝶的正反饋或負反饋的作用。具體表現受生物互惠互利的行為機制影響，讓蝴蝶受到比自身適應度好的個體的正反饋作用以及比自身適應度差的負反饋作用，從而使得蝴蝶能夠感知到更多方向的位置信息，增強蝴蝶的全局搜索能力。

從搜索空間中隨機選擇一只蝴蝶，與當前蝴蝶、最優蝴蝶構建香味反饋機制實現信息共享。在飛行過程中，蝴蝶散發的香味會向不同方向傳播，為搜索空間中其他蝴蝶尋優提供有利信息。因此，假設每只蝴蝶能向兩個不同方向傳播香味，然后決定它將飛向哪個方向，兩個傳播方向分別是隨機蝴蝶所在方向和最優蝴蝶所在方向。通過香味反饋機制，當前蝴蝶根據傳遞的香味信息能夠知道食物是否在這兩只蝴蝶周圍。若隨機蝴蝶的適應度比當前的蝴蝶的適應度更好，則認為該食物存在，否則附近沒有食物來源。

如果食物源被證實存在于兩只蝴蝶的周圍，通過正反饋作用，當前蝴蝶會移動到兩只蝴蝶周圍。如果不是，通過負反饋作用，它向最好的蝴蝶移動。數學模型描述如下：

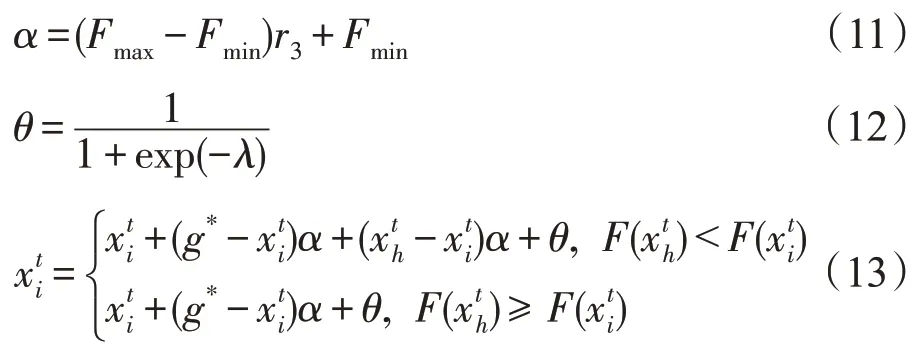
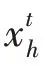
香味反饋機制使得蝴蝶個體可以更多地圍繞最佳位置進行挖掘，同時式（13）提出的飛行方向使蝴蝶個體運動方向具有多樣性化的能力，可以增強探索能力，特別是在迭代的初始階段，可以避免過早收斂。

2.3 群體協同效應位置更新機制

標準BOA中計算蝴蝶之間距離計算方式存在如下缺陷：（1）更新后的蝴蝶個體對前一次迭代的蝴蝶會產生很強的依賴性，具有一定盲目性致使算法出現停滯，從而導致收斂速度下降。（2）算法全局搜索和局部開發的能力受到很大限制，這也是標準BOA算法尋優精度不高的主要原因。為了進一步提升和平衡標準BOA 算法的全局搜索和局部搜索能力，受文獻[16]和文獻[17]共同啟發，本文將黃金正弦算法作為媒介，提出群體效應位置更新機制，針對式（5）、式（6），進行如下改進。

其一，利用黃金分割數不需要梯度信息的優點，對標準BOA算法的距離公式進行改進；其二，群體協同效應主要由個體矯正因子和群體協調因子構成，其利用正弦曲線值域分布特點，具體如下：

新局部搜索公式：

新全局搜索公式：

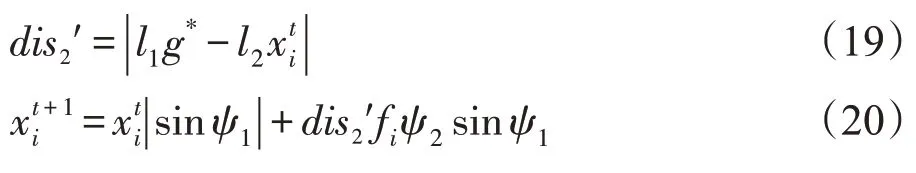
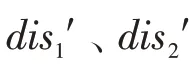
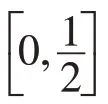
綜上三節，利用混沌初始化種群，使得種群分布更加均勻，為后續算法尋優打下基礎。通過反饋共享，引入隨機蝴蝶加快蝴蝶種群之間的信息交流實現信息流動達到共享，增強算法跳出局部最優能力。引入群體協同，降低蝴蝶的盲目依賴性，增強及平衡全局和局部搜索能力。尋優過程中，蝴蝶種群能夠進行針對性的搜索，調整適合個體進化方向，進而增強算法尋優能力。

2.4 改進算法的步驟

CFSBOA算法：

2.5 時間復雜度分析

CFSBOA算法主要由混沌初始化、反饋共享及群體協同效應組成，假設種群規模為，搜索空間維度為，則BOA的隨機初始化的時間復雜度為(×)，計算個體適應度為()，迭代過程中的時間復雜度為(×)，更新最優解的時間復雜度為(1)，BOA總的時間復雜度為(×)。

同理，CFSBOA 在BOA 的基礎上將隨機初始化替換為混沌初始化時間復雜度為(×)，增加的反饋共享機制的時間復雜度為(×)，增加的群體協同機制的時間復雜度為(×)，因此CFSBOA總的時間復雜度為(×)。因為CFSBOA和BOA的時間復雜度一樣，所以CFSBOA并未對算法產生負面影響。

3 實驗仿真與結果分析

實驗環境為Windows 7，64 位操作系統，CPU 為Intel Core i5-6500H，主頻3.2 GHz，內存8 GB，算法基于MATLAB2014b編寫。

為了充分驗證本文所提出的CFSBOA在求解復雜優化問題時的魯棒性和有效性，將CFSBOA 算法與加入混沌初始化的蝴蝶算法（chaotic butterfly optimization algorithm，CBOA）、加入反饋共享機制的蝴蝶算法（feedback butterfly optimization algorithm，FBOA）、加入群體協同效應的蝴蝶算法（sharing butterfly optimization algorithm，SBOA）、BOA、MFO（mothflame optimization）、SSA（salp swarm algorithm）和GWO（grey wolf optimize）在12個經典測試函數上進行最優值求解，然后進行實驗對比。

采用如表1 所示的12 個基準測試函數作為目標函數，測試函數包含單峰可分（unimodal sepa-rable，US）、單峰不可分（unimodal non-separable，UN）、多峰可分（multimodal separable，MS）、多峰不可分（multimodal non-separable，MN）等不同特征的函數。同時，測試函數的維度跨度大，從2維到200維，因此可以更加全面地檢驗算法的綜合性能。

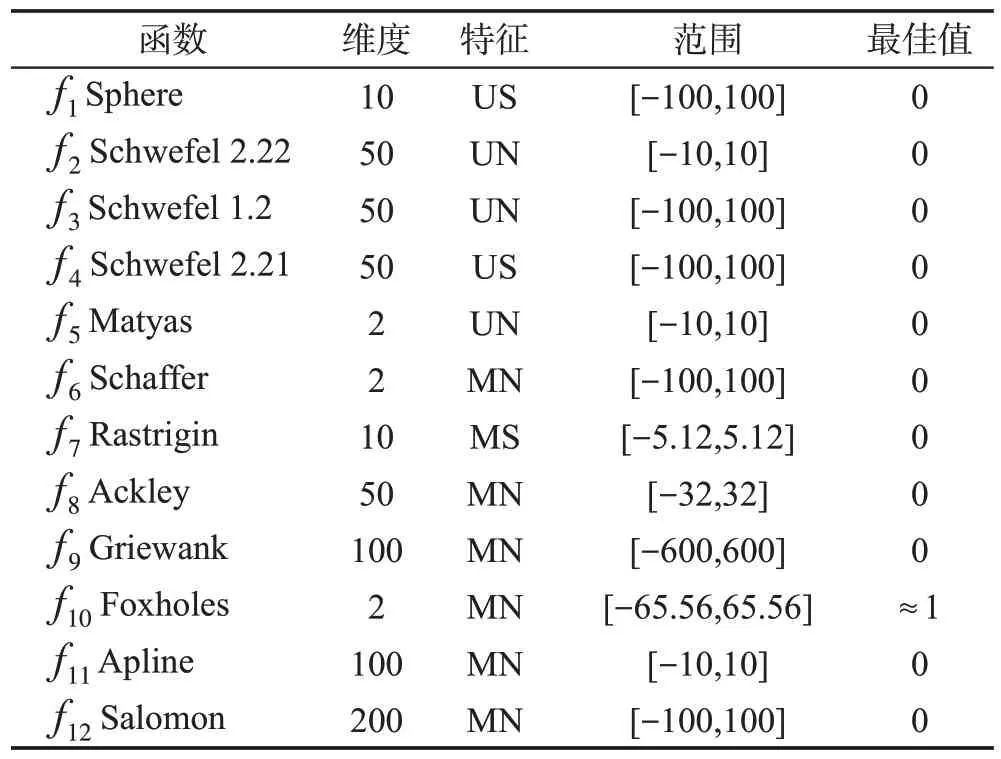
表1 基準測試函數Table 1 Benchmark functions

為保證每種算法對比的公平性，實驗中最大迭代次數設為500，種群規模為30，獨立運行50 次，其余參數設置如表2所示。

表2 主要參數Table 2 Main parameters

表3 通過最優值、平均值、標準差、成功率（success rate，SR）以及平均耗時（單位：s）五個性能指標來評估各算法的性能，實驗對比數據如表3所示。其中，成功率是計算成功次數與實驗的總次數之比，一次求解成功率公式如下：

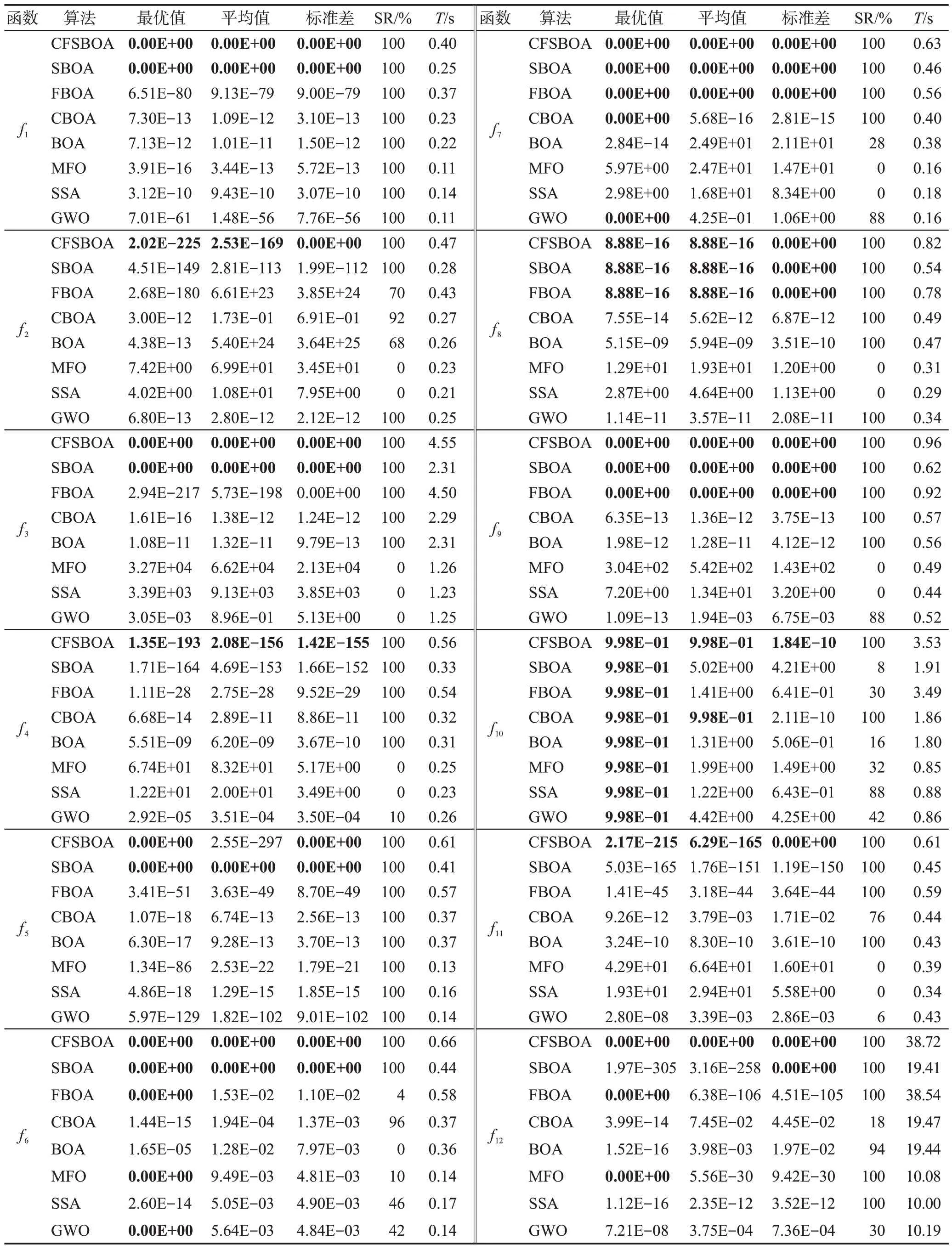
表3 基準測試函數結果對比Table 3 Results comparison of benchmark test functions

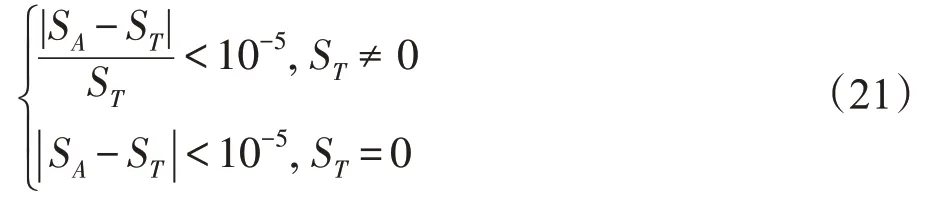
式中，S為每次求解的最優值，S為基準測試函數的最佳值。

首先，表3通過最優值和平均值來反映算法的尋優精度和收斂速度的能力。對于5個單峰函數～，CFSBOA對、和函數求解時，找到了理論最佳值。隨著函數維度增加，算法求解最優值的難度也將呈指數增長，因此在和函數上尋優精度有所降低，并未尋到理論最佳值。伴隨著函數維度的增加，對比算法MFO、SSA 和GWO 的精度有所下降，尤其是在求解50 維的時，MFO 與理論最佳值相差1.0×10的量級。對于CBOA、FBOA 和SBOA 的尋優精度和收斂速度，三種改進策略得到的結果均比BOA 好，這充分證明了不同改進策略對算法的尋優能力均有不同程度的增強。在5個單峰函數上，除上CFSBOA 的平均值略微高于SBOA 外，CFSBOA的綜合性能均比其他幾種算法好。對于7 個多峰函數～，與單峰函數相比，多峰函數的求解會變得更加困難，因此尋優精度低于單峰函數。隨著多峰函數維度增加，CFSBOA在對7個多峰函數求解時，5個多峰函數上能尋到理論最佳值。對7 個多峰函數尋優時，CFSBOA、SBOA 和FBOA 算法的尋優能力均優于標準的BOA，CBOA僅在的尋優能力不如BOA，但在其他函數的尋優能力均強于標準BOA。在上，CFSBOA、SBOA 和FBOA 的尋優精度和收斂速度都比其他算法要好。在上，各算法都找到理論最佳值，但CFSBOA 的平均值和標準差均比其他算法好。其余函數的求解上，CFSBOA 都能尋到理論最佳值，進一步驗證了三種改進策略的尋優有效性。由此可見，CFSBOA 對單峰可分、單峰不可分、多峰可分和多峰不可分及高維度的基準測試函數有著明顯的優勢。

其次，表3中成功率和標準差體現算法跳出局部最優的能力及穩定性。CFSBOA 的結果很接近理論最佳值，標準差也比較小，對基準測試函數尋優有著較強的穩定性。在12 個基準測試函數上，CFSBOA的尋優成功率都是100%，SBOA 在11 個函數尋優成功率為100%，FBOA在9個函數成功率為100%，雖然CBOA在～的成功率不如標準BOA，但其在8個函數上尋優成功率為100%，而標準BOA只在7個函數上成功率為100%。另外，隨著基準測試函數維度增加，標準BOA的尋優精度不高的特點愈發明顯，精度大多停留在10以下，而CFSBOA 和FBOA 引入的反饋共享機制，增加算法逃離局部最優能力，尋優精度得到提高；CFSBOA和SBOA引入群體協同效應使得算法的尋優精度和收斂速度大幅提升，證明了反饋共享機制和群體協同效應機制對算法的局部和全局搜索能力有很大的增強作用。

最后，從平均耗時角度分析。由表3 可知，MFO和SSA 的平均耗時最短，改進算法相對標準BOA 平均耗時都要長，因為改進策略中引入更多的機制使得算法不僅能在搜索空間中進行大范圍搜索，還能找到更多的解，所以導致算法平均耗時變長，但是CFSBOA 的平均耗時與其他算法相比，所增加部分在可接受范圍內。

為了形象地觀測改進策略的性能，對CFSBOA與SBOA、FBOA、CBOA、BOA、MFO、SSA 與GWO進行收斂性分析。圖2 給出部分測試函數的平均收斂曲線圖。因為尋優精度較高，為了便于觀察平均曲線的收斂情況，本文的縱坐標取以10為底的對數。

在單峰函數上，CFSBOA 的尋優精度最高，SBOA 其次，其余算法的尋優精度都不高，同時CFSBOA 的收斂速度最快。在上，尋優精度依次為CFSBOA、SBOA 和FBOA，其余算法的精度不高，CFSBOA 相比其他算法求解最佳值的迭代次數更少并且能夠快速收斂。

在多峰函數上，所有算法未能尋到最佳值，但CFSBOA、SBOA 和FBOA 的尋優性能突出，尋優精度比其他算法高，CFSBOA和SBOA能夠快速收斂到精度較高的解上且收斂速度較快。在上，所有算法都尋到最佳值，但CFSBOA 和CBOA 收斂速度最快，CBOA對于該函數的尋優能力相比其他函數優勢突出。在上，CFSBOA雖未能尋到最佳值，但尋優精度最高且相比其他算法收斂速度快。在上，CFSBOA 和FBOA 都能尋到最優值；對于收斂速度，CFSBOA 收斂速度最快，FBOA 其次，SBOA 慢于兩者，其余算法收斂速度慢且收斂精度低。

另外，由圖2（a）～（f）可以看出，在種群迭代前期，CFSBOA、SBOA 和FBOA 曲線速度下降很快且尋優精度很高，說明引入群體協同機制和反饋共享機制能夠增強算法跳出局部最優的能力，使得算法在迭代開始時收斂速度變快。隨著迭代的進行，CFSBOA能夠持續尋優，而其他算法在迭代后期陷入局部最優出現停滯狀態。同時，在上，CFSBOA比只增加反饋共享機制的FBOA 收斂速度更快且尋優精度更高，證明了群體協同效應機制，通過對個體和群體的協同配合使得種群逃離局部最優和全局搜索的能力得到增強，有利于算法的持續尋優。在上，CFSBOA 比只增加群體協同效應的SBOA收斂速度更快，這證明反饋共享機制能幫助算法快速找到最優解位置附近。另外，CFSBOA在和上尋到了基準測試函數的理論最佳值。除了在上，FBOA 的平均收斂曲線和標準BOA 平均收斂曲線在一個數量級上，其余改進算法的平均曲線都在標準BOA算法平均收斂曲線的下方，驗證了改進算法的有效性。結合表3 和圖2的實驗結果和平均收斂曲線圖證明，不管基準測試函數是單峰、多峰，還是在低維、高維，CFSBOA的綜合性能均比其他算法要好。圖2（b）和圖2（f），因縱坐標取對數的原因加上CFSBOA在這兩個函數上找到了0，所以曲線后面沒有顯示。

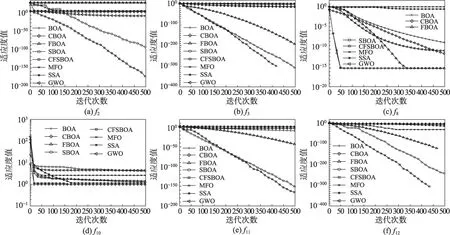
圖2 基準測試函數平均收斂曲線Fig. 2 Average convergence curve of benchmark test functions

根據Derrac等人在文獻[21]中提出的，對于改進進化算法性能的評估，需要進行統計檢驗。本文選擇用Wilcoxon 秩和檢驗并在5%的顯著性水平下進行。表4 給出了CFSBOA 和其他算法在所有基準測試函數上的值。假設CFSBOA 為最佳算法，則在CFSBOA vs SBOA、CFSBOA vs FBOA等之間進行成對比較。另外，由于最佳算法與自身無法進行比較，因此針對最佳算法采用N/A標記，代表“不適用”，符號“=”“+”和“-”分別代表相當于、優于、劣于對比算法。Derrac 等人的文獻中指出值小于0.05 認為是拒絕零假設的有力驗證。表4結果表明，CFSBOA的值基本小于0.05。只有在、的CFSBOA vs CBOA時，值大于0.05。這表明CFSBOA算法的優越性在統計檢驗上是顯著的。因此可以認為CFSBOA算法比其他算法具有更高的收斂精度，值大于0.05已用粗體顯示。

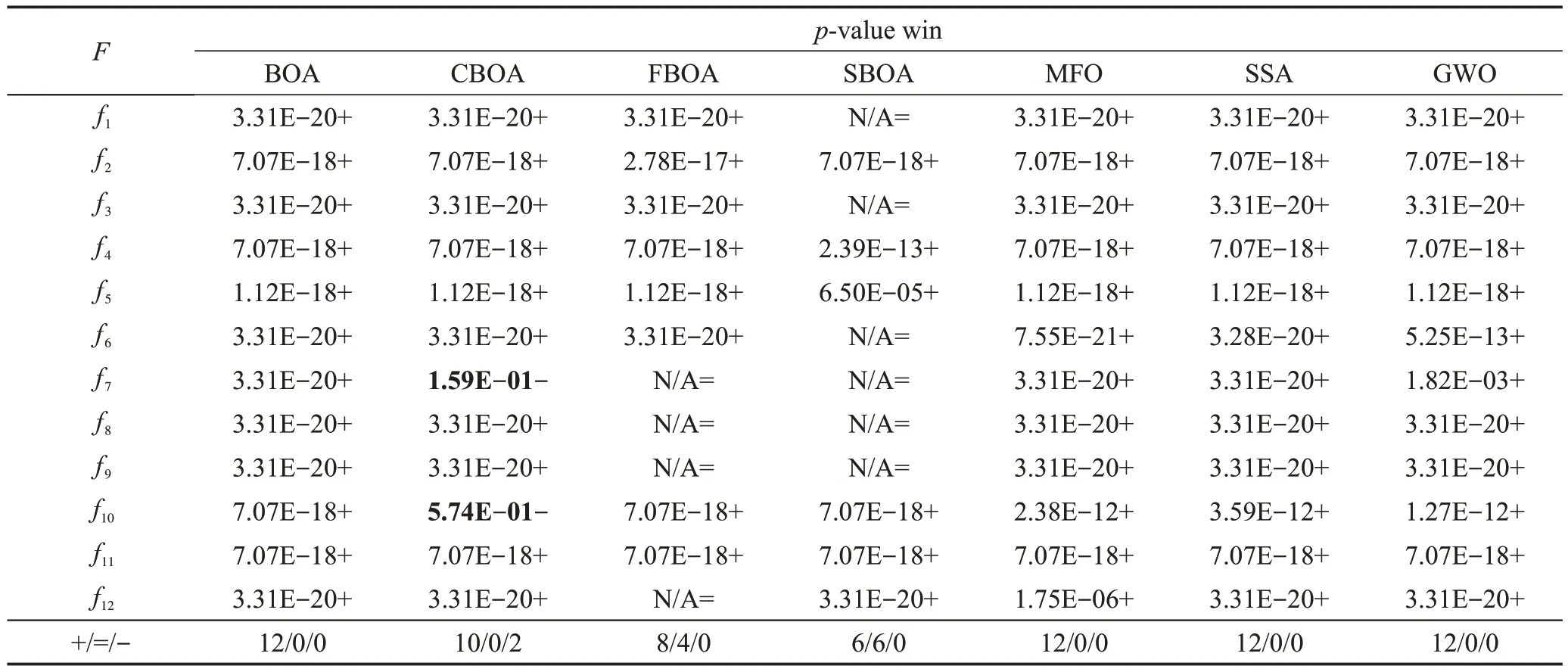
表4 基準函數Wilcoxon秩和檢驗的p 值Table 4 p value for Wilcoxon's rank-sum test on benchmark functions

文獻[22]提出使用平均絕對誤差（mean absolute error，MAE）對優化算法進行排序，這是一種有效且可行的性能指標。表5 中所有算法的分析是基于12個基準測試函數的MAE。MAE公式如下：

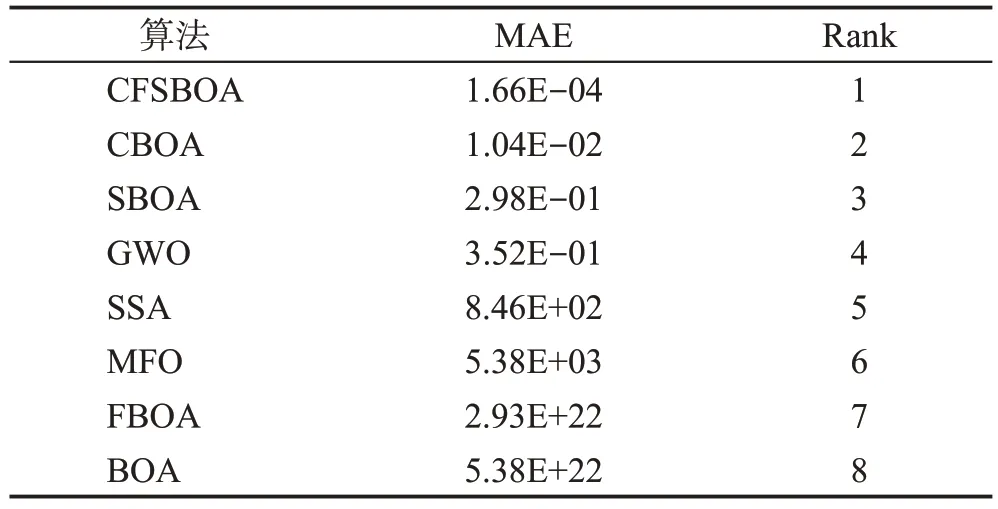
表5 各算法MAE排名Table 5 MAE ranking of each algorithm

式（22）中，B為算法最優值的平均值；V為相應基準函數的理論最優值；N為基準函數個數。

由表5 可知，CFSBOA 排名第一，CBOA 排名第二，SBOA 排名第三。同時，與另外七種算法相比，CFSBOA的MAE值最小。表5的實驗數據進一步表明了CFSBOA算法的有效性和魯棒性。

為了更進一步評估CFSBOA 的有效性和魯棒性。實驗2 分為兩個環節：第一環節主要采用CEC2014 函數對CFSBOA 的綜合性能進行驗證；第二環節驗證CFSBOA的競爭性，在保證種群規模、迭代次數、獨立運行次數及基準測試函數維度相同的條件下，將其與目前改進蝴蝶優化算法及新改進的群智能算法進行公平對比。

本文在CEC2014測試函數選取部分單峰、多峰、混合(hybrid function，HF)及復合(composition function，CF)函數類型進行驗證，所選CEC2014部分函數如表6所示。為了保證算法對比公平性，將種群規模設為30，CEC2014函數的搜索維度設為30，迭代次數500，獨立運行30次，實驗結果如表7所示。

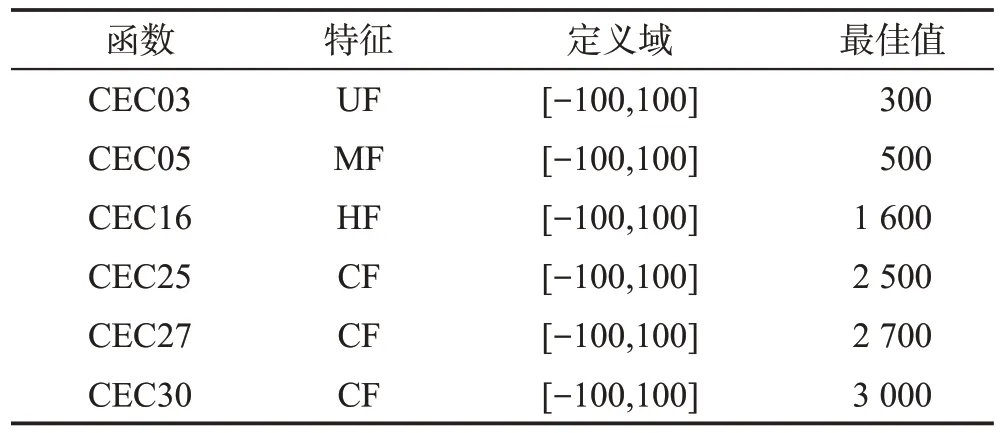
表6 CEC2014函數（部分）Table 6 CEC2014 function(part)

表7 分別記錄各種算法的平均值和標準差，因CEC2014函數較為復雜，很難找到最佳值。由表7可知，CFSBOA 在CEC03 的平均收斂不如GWO 和PSO，但標準差遠低于兩者；在CEC05和CEC16函數的平均值略低于GWO、MFO、SSA 和PSO，但CFSBOA的標準差低于四種算法。另外在最后三個函數上，CFSBOA 算法的平均值和標準差均低于其他算法，驗證CFSBOA算法的魯棒性和有效性。

表7 CEC2014測試函數的結果對比Table 7 Comparison of CEC2014 test function results

與參考文獻中數據進行對比，每個算法的種群規模設為30，迭代次數為500，基準測試函數搜索維度為30，對獨立運行30 次后的結果進行對比，其中“—”代表無數據，如表8所示。

由表8可知，CFSBOA算法在、、、、和函數上平均值均為最佳值；在和函數平均值高于MSIWOA（multi-strategy improved whale optimization algorithm）算法和CWBOA（Cauchy variation and adaptive weight butterfly optimization algorithm）算法；在上，CFSBOA算法尋優性能不如MSIWOA算法；在上，CFSBOA的標準差高于MPA（marine predator algorithm），而在其余函數上CFSBOA算法的平均值和標準差低于其他算法。因此，本文提出的CFSBOA算法在求解復雜優化問題上具有一定的競爭性。

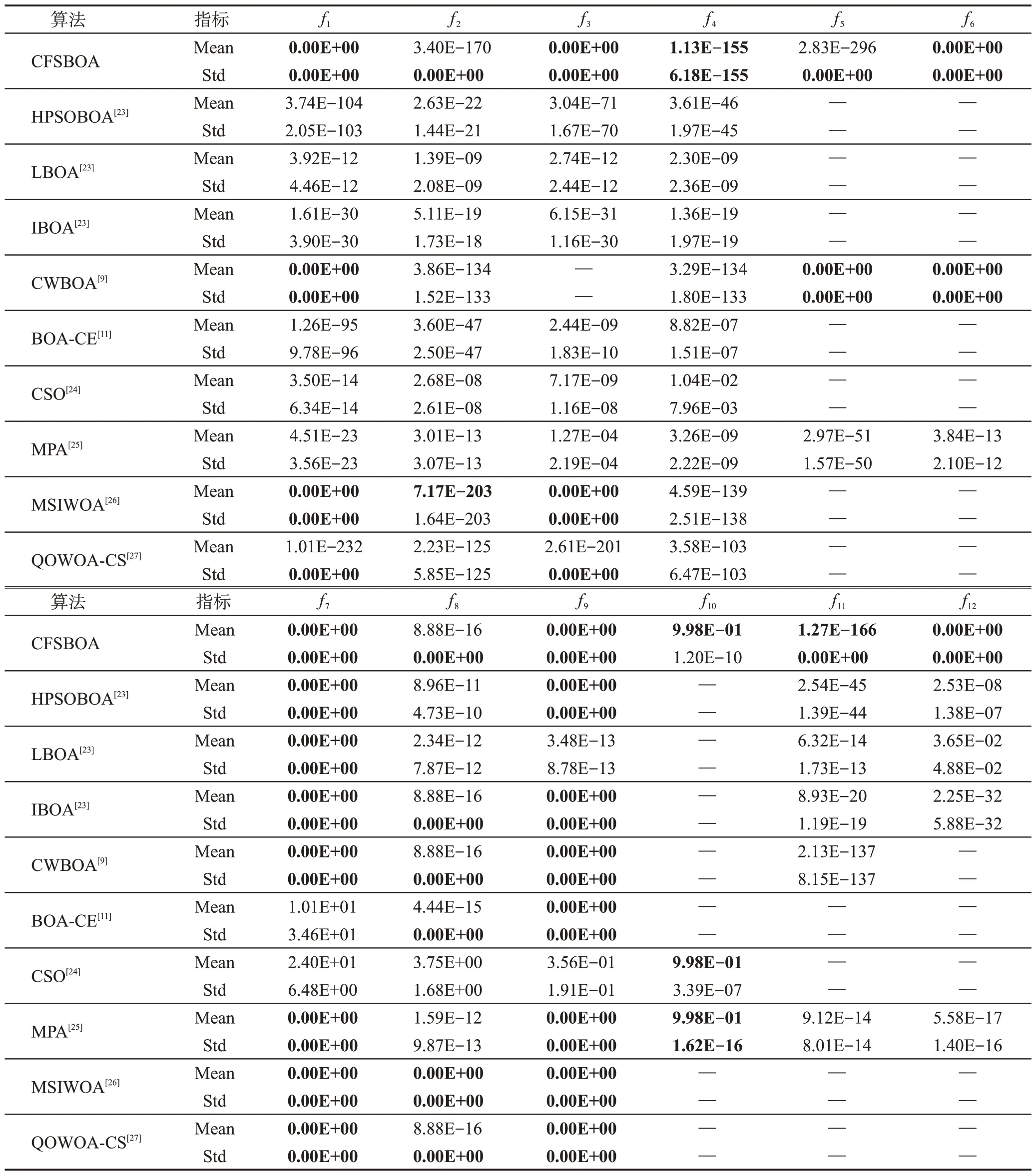
表8 與參考文獻中算法平均值和標準差的結果對比Table 8 Results comparison of mean and standard deviation of algorithms in references

綜上所述，實驗1 和實驗2 的實驗結果充分證明了混沌反饋共享和群體協同效應的蝴蝶優化算法對于求解多種類型的基準測試函數，尤其是多峰、高維的函數具有較好的魯棒性和較高的尋優精度。

4 結束語

為了增強標準BOA算法的跳出局部最優的能力及提高算法的尋優精度和加快收斂速度，本文提出了混沌反饋共享和群體協同效應的蝴蝶優化算法，并將改進的蝴蝶優化算法應用于基準測試函數和CEC2014 函數尋優。混沌機制對種群進行初始化，增加種群的多樣性，該機制對特定函數優勢明顯；迭代過程中，通過利用正負反饋的原理，構建反饋共享網絡使得蝴蝶信息來源更加多元，增強算法逃離局部最優的能力；利用群體協同效應平衡和增強算法的全局和局部搜索能力，提高尋優精度和加快算法收斂。三個改進機制能增強算法跳出局部最優的能力，同時提高尋優精度和加快算法收斂能力。另外，本文不僅使用最優值、標準差等指標對算法評估，還使用統計檢驗Wilcoxon 對算法進行顯著性分析和MAE 排序各算法，實驗結果表明CFSBOA 算法具備出色優化性能，全局和局部搜索能力得到增強，能夠收斂到精度更高的最優解，同時算法的有效性和魯棒性也得到驗證。

在未來，準備改進混沌機制增強其對測試函數的一般性以及將改進的蝴蝶優化算法應用于實際的工程優化問題，解決工程問題的同時，進一步驗證算法的性能。