建筑地基深基坑開挖底面變形風險控制研究

李 帥 杜立杰 張 杰 樊翠銀

（ 北京速測信息科技有限公司，北京 100080）

0.引言

隨著建筑施工技術的不斷成熟，對建筑地基深基坑開挖底面變形的控制精密度要求也越來越高。 采用有限元技術， 建立建筑地基深基坑開挖底面變形風險控制模型，通過有限元特征分析和承載應力分析的方法，在裂縫模式和拉壓薄膜效應模式下進行建筑地基深基坑開挖底面變形特征分析，采用薄膜效應階段荷載-位移曲線分析，建立建筑地基深基坑開挖底面變形風險控制曲線分布模型，通過極限應力特征分析， 實現構件的整體結構分析和風險控制。

目前， 國內外學者對建筑地基深基坑開挖底面變形風險控制的研究較多， 包括基于雙向板承載力計算的變形風險控制方法、 基于微分方程和艾里應力函數水平約束的風險控制方法、基于三階段荷載-變形模式的變形風險控制方法等[2,3]。 文獻[4]中提出基于鋼筋應變差的混凝土雙向板極限狀態分析及地面變形風險控制方法， 結合板殼有限元理論，編程計算建筑地基深基坑開挖底面變形特征，但該方法沒有考慮受拉薄膜效應的影響， 變形風險控制的適應度不高。 文獻[5]中提出型鋼混凝土異形柱基于損傷的恢復力模型及變形控制方法，考慮二階矩效應、軸壓附加抗側剛度、強度衰減，通過參數控制，實現建筑地基深基坑開挖底面變形風險控制，但該方法對變形控制的擬合度不高。針對上述問題，本文提出基于彈性段-強化段為雙折線擬合控制的變形風險控制方法。 首先建立建筑地基深基坑開挖底面變形的試件參數分析模型， 通過對不同工況的底面變形風險差異度分析， 然后進行鋼筋和混凝土間粘結滑移作用分配和承載力計算，最后進行實驗測試，展示了用本文方法進行建筑地基深基坑開挖底面變形風險優化控制能力方面的應用性能。

1.試件結構模型

建立建筑地基深基坑開挖底面變形的試件參數分析模型， 在進行建筑地基深基坑開挖底面的變形特征分析中，基地在無窮遠處受靜水壓力的作用，忽略重度梯度的影響。 結合構件滯回特性分析，通過松弛等力學行為參數分析，進行建筑地基深基坑開挖底面的應力評估和屈服響應分析。基于Maxwell體和Kelvin模型，進行時效變形行為特征分析， 采用Burgers蠕變模型進行Abel黏性元件的本構特征分析，實現對建筑地基深基坑開挖底面變形的結構參數模擬。 采用串聯法則，進行微分-積分卷積計算，以Maxwell體和Kelvin模型為基礎，通過虎克彈性體本構特征分析，得到建筑地基深基坑開挖底面變形的Burgers蠕變模型（ 如圖1所示）：

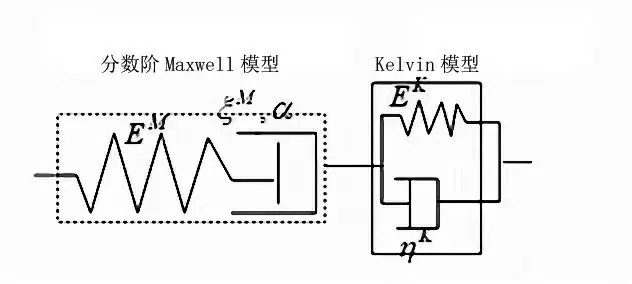
圖1 建筑地基深基坑開挖底面變形的Burgers 蠕變模型

由圖1可知：ηK為虎克彈性體的本構系數；EM為黏滯系數；ξM為應力參數；α為受靜水壓力作用下的變形系數。 在基于圍巖與襯砌的相互作用下， 采用圍巖與襯砌的相互控制，進行變形風險抑制，得到建筑地基深基坑開挖底面變形結構參數（ 如表1所示）：

表1 建筑地基深基坑開挖底面變形結構參數

根據表1試件設計模型參數， 采用網格結構模型構建襯砌柵和支護結構柵，進行變形風險控制（ 如圖2所示）：

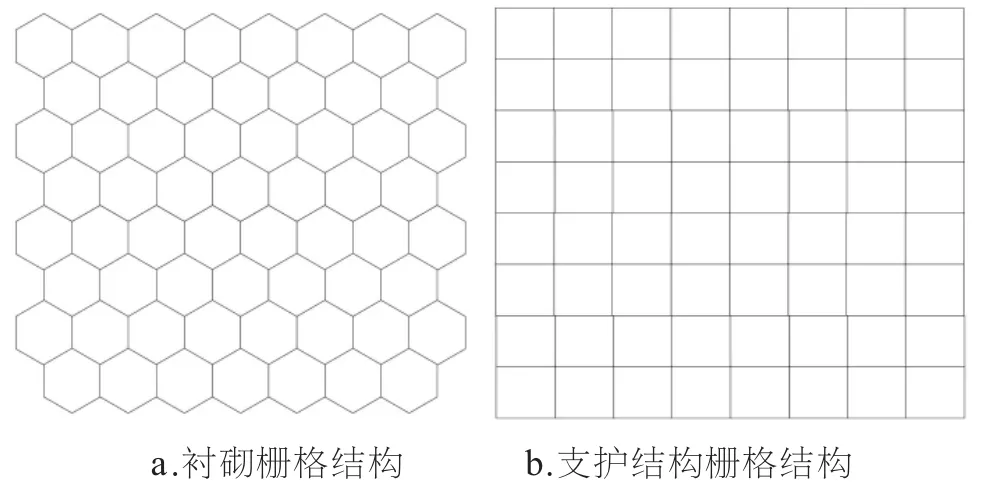
圖2 變形風險控制的柵格結構

2.開挖底面變形沉降模態分析

搖搖結合構件滯回特性分析， 采用最大累計沉降控制方法分析建筑地基深基坑開挖的沉降模態，給出建筑地基深基坑開挖底面變形沉降風險控制的約束參數和變量含義描述如下：X為對屈服后(受拉薄膜效應)階段混凝土中心的位移；θ為混凝土壓碎破壞的模型參數；δ，δ2分別為建筑地基深基坑開挖底面變形下塑性鉸線的損傷系數和抗拉強度；MP,MR分別為y方向兩鋼筋應變測點；JR=JRL=JRR,JPθ,JPδ分別為雙向板薄膜效應機理參數及鋼筋應變， 表示約束轉動慣量參數；R為混凝土簡支板承載參數；L為最大裂縫寬度；D為試驗板荷載-撓度距離; Km,Ke為裂縫開展和鋼筋屈服；UL,UR為最大裂縫寬度及傳導系數。 以上各變量均采用國際單位。 采用有限元分析方法進行建筑地基深基坑開挖底面變形的應力屈服響應分析。

假設建筑地基深基坑開挖的單元應力向量為n， 應變向量為ξ，則基底跨中出現大量網狀裂縫表達如式（ 1）所示：

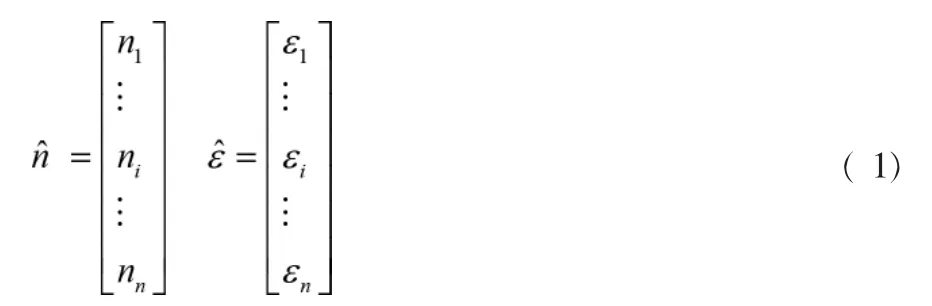
式（ 1）中，ni，εi分別為各個測量點的裂縫開展度和鋼筋屈服。 在最大應力狀態下，最大裂縫寬度約為0.2mm，引入抗彎剛度軟化系數， 得到荷載-平面內位移分布的彈性模量關系Gn表示為：

其中，

式（ 4）中，E為獲得后期壓力數據的彈性模量；Si為第i組變形位置節點的板角約束力；Ai為單位跨中豎向撓度。

根據上述分析，建立了建筑地基深基坑開挖底面變形的試件參數分析模型， 通過位移邊界條件層面分析的方法，采用ANSYS有限元軟件建立有限元模型。

3.開挖底面變形風險控制模型優化

通過ANSYS 有限元軟件模擬基深基坑開挖底面的彈性段-強化段雙折線分布問題， 通過對不同工況的底面變形風險差異度分析， 計算后期各板角約束力的水平位移之和，如式（ 5）所示：

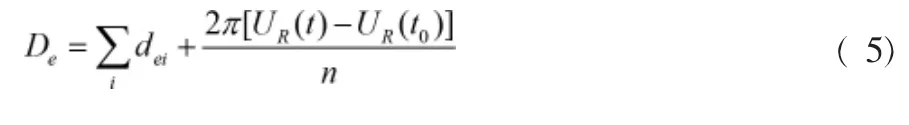
式（ 5）中，dei為支護結構相互作用矩；UR為偏應力；n為高壓縮性元件的個數；t0為巖體的不可壓縮特征參數。進而得到底面彈性變形的高壓縮性元件滿足Ds，如式（ 6）所示：

式（ 6）中，Dr為支護壓力的積分截面數；δ為高壓縮性元件的個數；l為試件長度；E1為徑向和切向偏應力；σ為壓縮應力系數。構造混凝土襯砌的扭矩-扭轉角滯回曲線，分布曲線關系，如式（ 7）所示：

式（ 7） 中，Vt1為截面距掌子面的距離；Vu1為剪切模量；ΔVt為無限大平面孔洞映射差。 通過對不同工況的底面變形風險差異度分析，進行鋼筋和混凝土間粘結滑移作用分配和承載力計算，如式（ 8）所示：

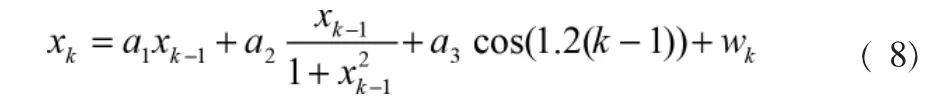
式（ 8）中，a1=1/2，a2=25，a3=8，a4=20，分別為1、2、3、4階巖土材料蠕變系數；k為巖體Abel黏性元件的本構參數；xk－1為虎克彈性體模型參數；wk為不同荷載下應力。 根據上述參數設計和拉薄膜效應、鋼筋強度破壞準則，實現對建筑地基深基坑開挖底面變形風險預測和控制。

4.實驗測試

為了驗證本文方法在實現建筑地基深基坑開挖底面變形風險控制中的應用性能，進行實驗測試。 建筑地基深基坑的高壓縮性元件長140cm，樁長43.5m，采用4種盾構施工參數分別開挖500m，斷面沉降值在5.2mm～5.3mm，開挖的盾構參數（ 如表2所示）:

表2 地基深基坑開挖的盾構參數

根據表2的參數設定，構建ANSYS有限元分析模型（ 如圖3所示）:

圖3 建筑地基深基坑開挖底面變形有限元分析結果

上述有限元分析結果能準確實現對地面變形的參數分析，得出襯砌結構及等代層參數（ 如表3所示）:

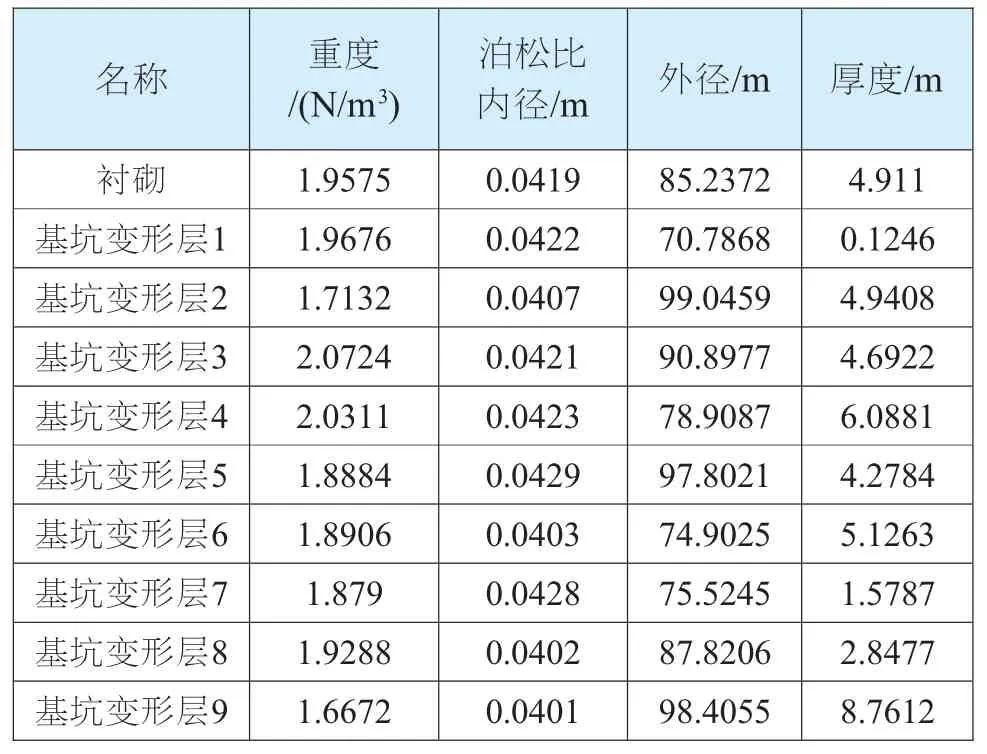
表3 襯砌結構及等代層參數

分析表3參數解析結果得知： 本文方法能有效實現對不同工況的底面變形風險預測。 測試預測的精度，得到對比結果（ 如圖4所示）:

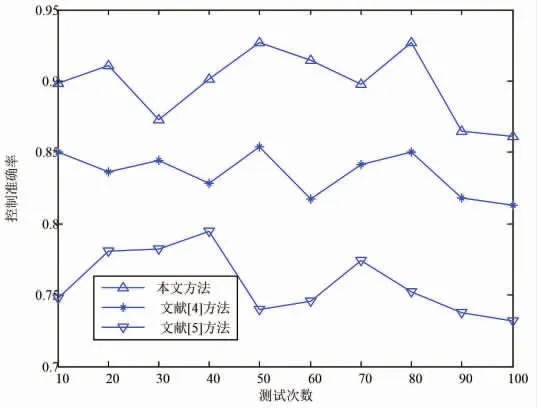
圖4 風險控制精度對比

5.結束語

建立建筑地基深基坑開挖底面變形風險控制曲線分布模型，通過極限應力特征分析，實現構件的整體結構分析和風險控制。 本文提出基于彈性段—強化段為雙折線擬合控制的變形風險控制方法。基于Maxwell體和Kelvin模型，進行時效變形行為特征分析， 采用Burgers蠕變模型進行Abel黏性元件的本構特征分析，實現對建筑地基深基坑開挖底面變形的結構參數模擬。 分析得出：用本文方法進行建筑地基深基坑開挖底面變形控制的參數解析能力較好，控制精度較高。