思維品質培育:數學課堂的應然追求

鄭錦云

思維品質，是指個體在思維活動中的智力特征。數學被稱作“思維的體操”，對提升個體思維的靈活性、深刻性、開闊性、全面性等品質有著積極的促進作用。如何在數學課堂教學中緊扣知識本質，精心設計活動，挖掘學生的思維潛力，培育良好的思維品質呢？下面筆者結合自己的實踐談談幾點看法。

一、巧引導，妙追問，提升思維靈活性

問題是數學的心臟。在數學課堂中，問題是導學引思的有效載體。巧妙的引導與追問能調動學生思維的積極性，打開學生思考的場域空間，發展思維的靈活性。在教學中，教師應深入剖析教材，細究知識本質，分解知識要素，形成若干個指向知識機理的核心問題，以此串聯課堂，調動思維。

例如，執教“認識負數”時，教師以“假如這世界沒有負數可以嗎？”“0是正數還是負數呢？”等問題搭建學習支架，引導學生從負數的價值、特點、應用三個層次，逐層深入對負數的認識。在對話“假如這世界沒有負數可以嗎？”時，學生各抒己見，展開了激烈的辯論，部分學生認為可以沒有負數，如果要表達“零下幾度”“低于海平面多少米”用文字即可，部分學生堅持一定要有負數，這樣表達起來更加簡便。正當雙方僵持不下時，教師進一步引導：“我們以前學了那么多數，為什么不夠用呢？”并追問：“以前的數表示什么？而負數可以表示什么？”在這樣的啟發誘導下，學生跳出原來的思維困局，明白生活中有許多表示相反意義的事物，正數表示其中一種，負數表示另一種。由此，學生理解了負數存在的意義，厘清了0與正數、負數之間的關系。教師通過追問，進行適時且恰當的點撥，幫助學生變換思路，點燃思緒，使其思維的靈活性得到很好的培育與發展。

二、多比較，重歸納，強化思維深刻性

比較與歸納是數學學習的重要方法，教學中，教師應引導學生在多個事物的觀察與比較中，抽象概括出事物所包含的共同特征，這樣既能有效深化學生對數學概念本質屬性的認識，又能切實塑造其思維深刻性的品質。

例如，在“乘法分配律”中，教師多次組織比較與歸納。其一，在情境的支撐下，學生得到兩組等式：（49+41）×12=49×12+41×12，（140+160）×2=140×2+160×2，此時，教師引導學生分別從橫向、縱向觀察兩組等式，學生在對比中發現：（1）都有相同的數字，結果也相同;（2）左邊都有括號，右邊都沒有括號;（3）運算順序不同，左邊是先算兩個數的和，再乘另一個數，而右邊是這兩個數分別和另一個數相乘，再相加。緊接著，引導學生舉例驗證、抽象歸納，建構乘法分配律的模型。其二，在練習環節，教師抓住了乘法分配律與乘法結合律兩個模型之間的混淆點，出示判斷題，引導學生在對比辨析中，把握乘法分配律的本質特點。其三，在課堂的最后，教師組織學生比較新知舊識，加深對乘法分配律的理解，在知識的縱向聯系中，學生發現原來在橫式、豎式計算中，就已經大量接觸了乘法分配律。上述教學過程，教師多次組織學生對材料進行觀察比較，并在此基礎上及時歸納提煉，助推學生對知識本質的深層內化，并借此錘煉思維的深刻性。

三、巧設疑，造沖突，延展思維開闊性

在學生的數學學習過程中，往往是按照已積累的思維活動經驗來展開數學思考，但同時也常常受固有思維的影響，陷入僵局而不自知。此刻，需要教師及時洞察學生的思維困境，巧妙設置問題，制造認知沖突，暴露思維的迷思點和局限性，沖破思維定勢的壁壘，從而發展思維的開闊性。

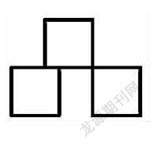
例如，在執教“長方形的面積”時，教師先以“根據面積大小猜測信封中的圖形”來導入，第一個要猜的圖形面積為1平方分米，學生很自然想到是邊長為1分米的正方形;第二個要猜的圖形面積為3平方分米，學生由于思維慣性使然，認為是3個邊長為1分米的正方形拼成的長方形。當揭曉答案為不規則圖形時（如右圖），在學生訝異之余，教師追問：“為什么想到的都是長方形？”學生從中反思：平常見到的一般都是長方形，忽略了別的不規則圖形。這是一次打開思維局限的嘗試，學生打破自身思維盲點，開闊思維的空間。

而后，在本課的拓展延伸環節，教師又設計了趣味性的習題，“老師家里也有一個面積為20平方厘米的長方形，猜猜看，它的長和寬可能分別是多少？”學生猜有可能長是20厘米，寬是1厘米，也有可能長是10厘米，寬是2厘米。教師追問：“長方形的長有可能比20厘米還長嗎？”有學生猜測不能，已經是20平方厘米，再擺下去就是21、22……已經是極限了。慢慢地，有學生認為可以，只要寬改成0.5厘米，長改成40厘米就行。教師繼續跟進：“長有可能比40厘米還長嗎？”此時，學生思維完全被打開，大膽猜測長很長、寬很短的情況，甚至繼續把寬縮短，長可以很長很長，長到無法計算。在教師的設計中，學生對面積與面積單位的探究經歷如體驗懸念迭起的劇情，也正是這樣的過程，激發了學生的思維活性，突破了思維局限，持續生成思維延展的道路。

四、多勾連，促遷移，發展思維全面性

數學是一個立體交互的知識系統，具有整體性、邏輯性、結構性的特點。在實際教學中，教師應具備“大概念”的教學理念，不能僅僅滿足于傳授單個知識，而是要引導學生知識、經驗的正向遷移，主動建構知識體系，同時也發展思維全面性。

例如，筆者研讀人教版、蘇教版、北師大版的教材發現，“小數的意義”一課均強化了小數與分數的關系，弱化小數與整數本質上的關聯。若按照教材循規蹈矩，并不利于學生形成對小數、分數、整數的整體認知，難以發展學生數學思維的全面性。在不少名師的課堂中，他們對小數意義的教學進行重構，以“1”為臨界點，不斷滿十進一，形成十、百、千、萬等，不足1則不斷十分，退一當十，精細為十分之一、百分之一、千分之一、萬分之一等。特別是吳正憲、羅鳴亮老師執教的《小數的意義》。在吳老師的課堂中，借助小方格、小方塊的直觀，演示1通過“漲”形成了10、100……1通過“縮”得到了0.1、0.01……羅老師以數數導入新課，喚醒計數中的“十進”經驗，而當所出示的方格涂色部分不足1時，學生數數出現了困難，產生了“十分”的需求，最后將“十進”聯系“十分”，深化對十進制的認知。兩個課堂都讓學生充分感受到小數與整數本質相通，體會小數是十進制計數法從整數擴展到分數的特殊形式。如此，學生不僅深刻理解了小數的意義，還建構了完善的認知體系，也促進學生思維的全面性和整體性。

思維品質是思維能力強弱的標志，培養良好的思維品質是發展智力、挖掘數學思維潛力的突破口。在數學課堂中，理應以培育思維靈活性、深刻性、開闊性、全面性為目標，實現以思維靈活性變化思路，以思維深刻性揭示本質，以思維開闊性解開束縛，以思維全面性健全體系。這樣，既滿足數學課堂提質增效的現實需求，又契合學生數學核心素養發展的真切訴求。

（作者單位：福建省福州市長樂區首占中心小學 責任編輯：念育琛）