基于ANSYS的橋梁顫振時域分析及程序實現

劉修平， 劉煥舉， 趙 越， 李光玲

(1.天水師范學院 土木工程學院，甘肅 天水 741000;2.河北工程大學 土木工程學院，河北 邯鄲 056038;3.長安大學 公路學院，西安 710064)

顫振是一種發散性氣動力自激振動，是橋梁風致振動當中最危險的振動形式。自Scanlan引入顫振導數描述鈍體橋梁自激力以來，分離流顫振機理在橋梁顫振分析應用中日趨完善[1-3]。然而隨著大跨纜索承重橋梁在跨越江海、深切峽谷的國家公路和鐵路交通控制性工程廣泛使用，結構非線性、氣動非線性等非線性因素對橋梁穩定性的影響也日益突出，風致顫振穩定性成了大跨橋梁設計施工過程中需考慮的關鍵性問題。由于Scanlan線性自激力模型不能很好的描述考慮各類非線性因素在顫振中的影響，在橋梁抗風研究日益精細的情況下，自激力時域模型研究成為了風致顫振分析的熱點[4-6]。

自激力的時域表達式有兩種方法：其一是Scanlan提出的Wagner在航空中提出的經典階躍函數表達法，其二是Buther & Lin提出的單位脈沖響應函數融入Roger有理函數的表達方法。張志田等[7]分別研究了兩種自激力時域表達式的瞬態特性及極限特性，提出了通過限定有理函數表達式若干參數克服瞬態特性模擬失真的方法；Chen等[8]基于有理函數表達的自激氣模型，提出了橋梁大跨度橋梁結構顫振分析的時域分析流程及特征值求解方法；郭增偉等[9-10]通過顫振導數的有理函數近似式得到自激力脈沖響應函數在橋梁顫振分析中的表現方式和求解方案，提出了顫振分析中初始響應失真及積分時間步長設定的解決方法；伍波等[11-12]發現相比經典階躍函數顫振分析方法，在考慮靜風效應的大跨度橋梁結構顫振特性分析中，有理函數自激力表達式模型可以有效減少計算風速下的迭代量，顯著提高計算效率。由于橋梁顫振非線性問題分析和方程求解的復雜性，一直以來，橋梁顫振時域分析多是基于C/C++、Fortran開發的專用程序進行[13-17]。近些年，隨著大型通用有限元分析程序在橋梁工程中具有廣泛的應用，基于通用有限元軟件ANSYS的顫振頻率分析方法日趨成熟，直接采用ANSYS進行橋梁顫振時域分析的研究較少。華旭剛等[18]基于ANSYS中MATRIX27矩陣單元建立了橋梁結構全模態顫振分析模型，提出以調整風速和振動頻率求解動力系統各階復模態特性的顫振頻域分析方法，曾憲武等[19]基于MATRIX27矩陣單元對自激力以單元氣動阻尼矩陣和單元氣動剛度矩陣提出了基于ANSYS的大跨橋梁抖振分析方法；為避免在使用過程中需假定振動頻率的步驟，謝煉等[20]利用了ANSYS內置的重啟動算法，迭代計算當前時步真實振動狀態，提出了橋梁顫振時域計算的重啟動法。

為避免MATRIX27矩陣單元輸入振動頻率的誤差干擾，同時簡化計算時步內的自激力反復迭代確定的重復過程。本文基于傳統有理函數自激力表達式推導處理，使得自激力表達式中的“記憶效應”項僅與上一時刻的橋面運動狀態相關聯，繼而重新形成有理函數自激力有表達式的質量項、剛度項、阻尼項和時間歷程項，建立基于MATRIX27矩陣單元的自激力時域模擬方法，并通過經典平板顫振分析成功驗證了所提方法的準確性。

1 橋梁斷面自激力

1.1 自激力有理函數表達

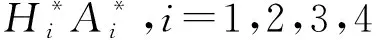
(1)

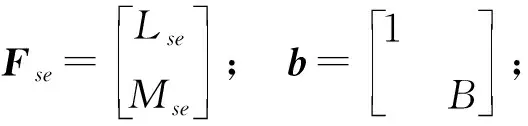
p=K(ξ+i)，ξ為橋梁結構阻尼比一般較小，可以忽略；其他參數含義如表1所示。

表1 8個顫振導數的參與振動方向Tab.1 Directions of eight aerodynamic derivatives

Scanlan自激力列式和振動圓頻率關聯，不具備直接進行時域分析計算的條件。Lin提出可以完全在時域中描述風致振動中產生的耦合氣動自激力的關系式，將之表達為

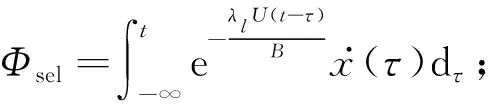
(4)

根據式(3)，有理函數推廣用于近似橋梁斷面自激力的氣動矩陣Q，形式為

(5)

式中：C1，…Cl+3均與頻率無關的氣動力系數；C1為自激力的氣動剛度項；C2為氣動阻尼項；C3為氣動質量項，其值一般較小，可以忽略；第4項以后都為自激力的記憶效應，與結構前一時刻和當前時刻的運動有關；λl為大于0的非定常項衰減常數。

1.2 氣動力系數識別

顫振導數的擬合對象為高度非線性的方程組，為避免大量的復數運算過程，令上述方程的實部和虛部相等，以升力的計算為例，則可以得到如下的關系式

(6)

該組方程式對應7個未知量，擬合過程需要參數共享，同時也要避免因初始值的影響陷入局部最優的問題。對于二維彎扭耦合顫振導數擬合共需識別28個氣動力系數，因此，優化迭代算法的選擇至關重要。

以理想平板顫振導數擬合為例，在最大迭代次數2 000、收斂誤差為1×10-10的設定下，分別采用常用的麥夸特法、擬牛頓法、遺傳算法、模擬退火算法、擬牛頓+通用全局優化算法求解上述方程組(2)式，求解結果和過程參數對比如表2所示。

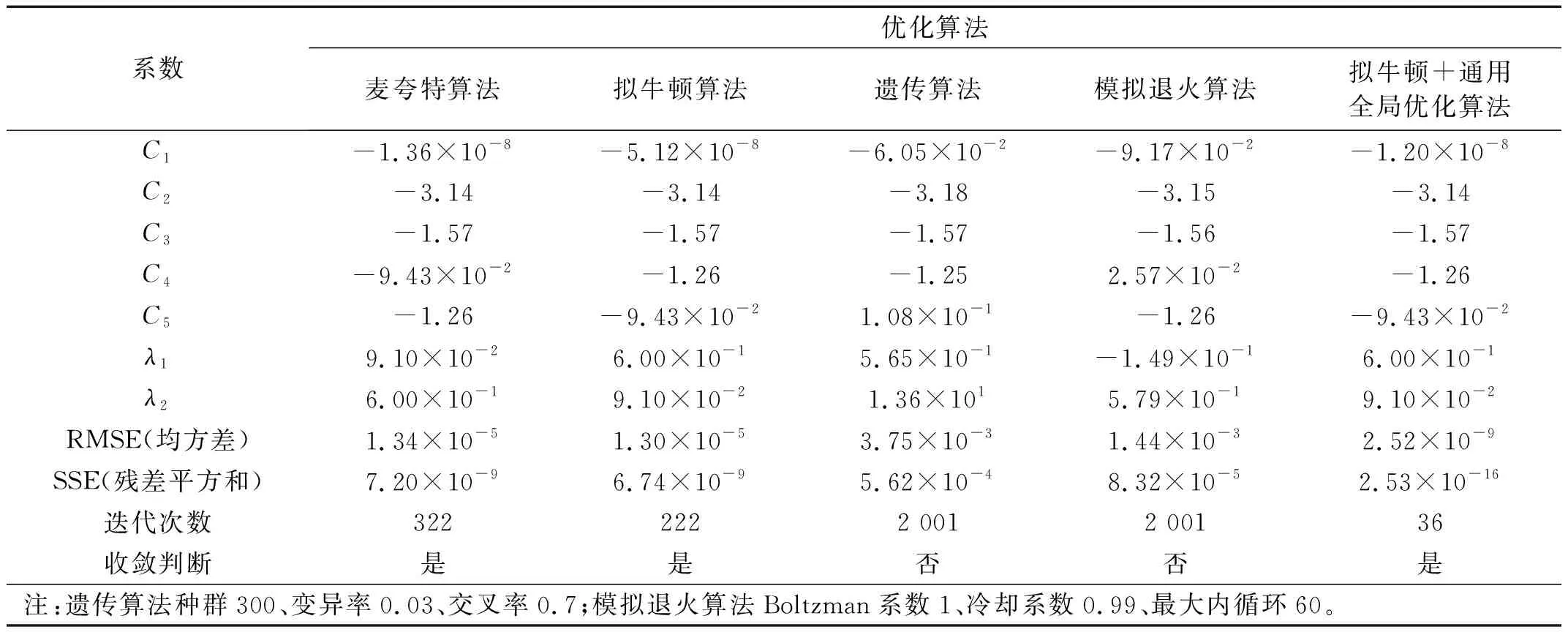
表2 不同算法求解結果比較Tab.2 Comparison of the results of different algorithms

由表2可知，在顫振導數擬合的實際計算中，求解此類方程組，麥夸特法、擬牛頓法和擬牛頓+通用全局優化算法都能快速的得到收斂解，而遺傳算法和模擬退火算法的計算效率較低，達到限定迭代步數后仍未收斂，同時對非定常項衰減常數λ計算值出入較大，甚至出現負值，顯然，考慮卷積積分Φsel的存在，λ應是大于0的實數。因此，在氣動力系數識別過程中應優先采用擬牛頓+通用全局優化算法。

2 基于MATRIX27的自激力時域模擬

2.1 MATRIX27矩陣單元的組集

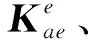
(7)

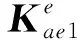
(8)

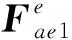
(9)

MATRIX27矩陣單元無幾何外形特性，其運動學響應用剛度、阻尼或者質量系數來指定，該矩陣單元連接2個節點，每個節點有6個自由度。在通過式(8)、(9)集成式(7)中的各矩陣后，將矩陣內的元素以實常數的方式賦予MATRIX27單元，并將其添加至結構單元的節點處，如圖3所示，時間歷程項作為外荷載形式輸入，從而形成時域自激力橋梁顫振分析有限元模型。

2.2 非線性項處理方法

時域自激力計算的難點在于非線性項的荷載受當前的時步ti和上一時步ti-1節點運動狀態共同影響，而商業有限元軟件ANSYS的瞬態分析是基于隱式算法，無法推算出當前時步的荷載。雖然可以利用重啟動實現了當前時步荷載的計算，但重啟動每個計算時步需迭代確定，在通用有限元程序中計算步數相對較多，耗時較長，對于大跨橋梁風致抖振分析而言效率并不高。因此，真正意義地實現基于MATRIX27矩陣單元的ANSYS時域顫振計算的前提就是將有理函數自激力表達式重新改寫，具體如下：

(1) 將非線性項重新改寫，以單位長度上扭轉運動對扭轉的影響為例。

(10)

(11)

引入，

那么，

(12)

利用Φsel(ti)和Φsel(ti-1)的關系可以得到

(13)

(2) 形成自激力有理函數表達的質量項、剛度項、阻尼項和時間歷程項。

在非線性項改寫的基礎上，那么，式(10)和式(11)可以表達為

(14)

(15)

令

(16)

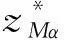
2.3 時程分析實現過程

橋梁顫振時域分析過程中，首先要顫振分析有限元模型施加一個初始激勵，由于自激振動系統的特征量，如頻率、衰減率等與初始激勵無關，在顫振分析時可對結構施加初始激勵，激勵形式可為集中力或者位移等，在ANSYS中的具體實現過程為：

(1) 假定計算風速。

(2) 施加任意初始荷載激勵。

(3) 計算第ti時刻的位移、速度和加速度向量。

(4) 計算ti+1時刻的荷載向量。

(5) 計算ti+1時刻的位移、速度和加速度向量。

(6) 依次重復步驟(4)、(5)，直到設置時間步完成。

(7) 計算此風速下結構振動時程響應的對數衰減率r，若r>0增加風速返回步驟(2)，若r<0減小風速返回步驟(2)，若r=0，則為顫振臨界風速，程序結束。

在步驟(7)中的顫振臨界風速確定時，可采用折半法查找，首先確定顫振臨界風速大致區間[Ul,Uh]，計算風速取Um=(Ul+Uh)/2，再進行迭代計算。同時，由于ANSYS中的APDL語言編程的限制，節點振動時程響應對數衰減率的計算可由MATLAB中的峰值讀數法函數直接進行，通過增加最小間隔條件，可以過濾掉單周期內的干擾極值，更準確的判斷振動是否衰減，在程序中迭代框架具體見圖1。

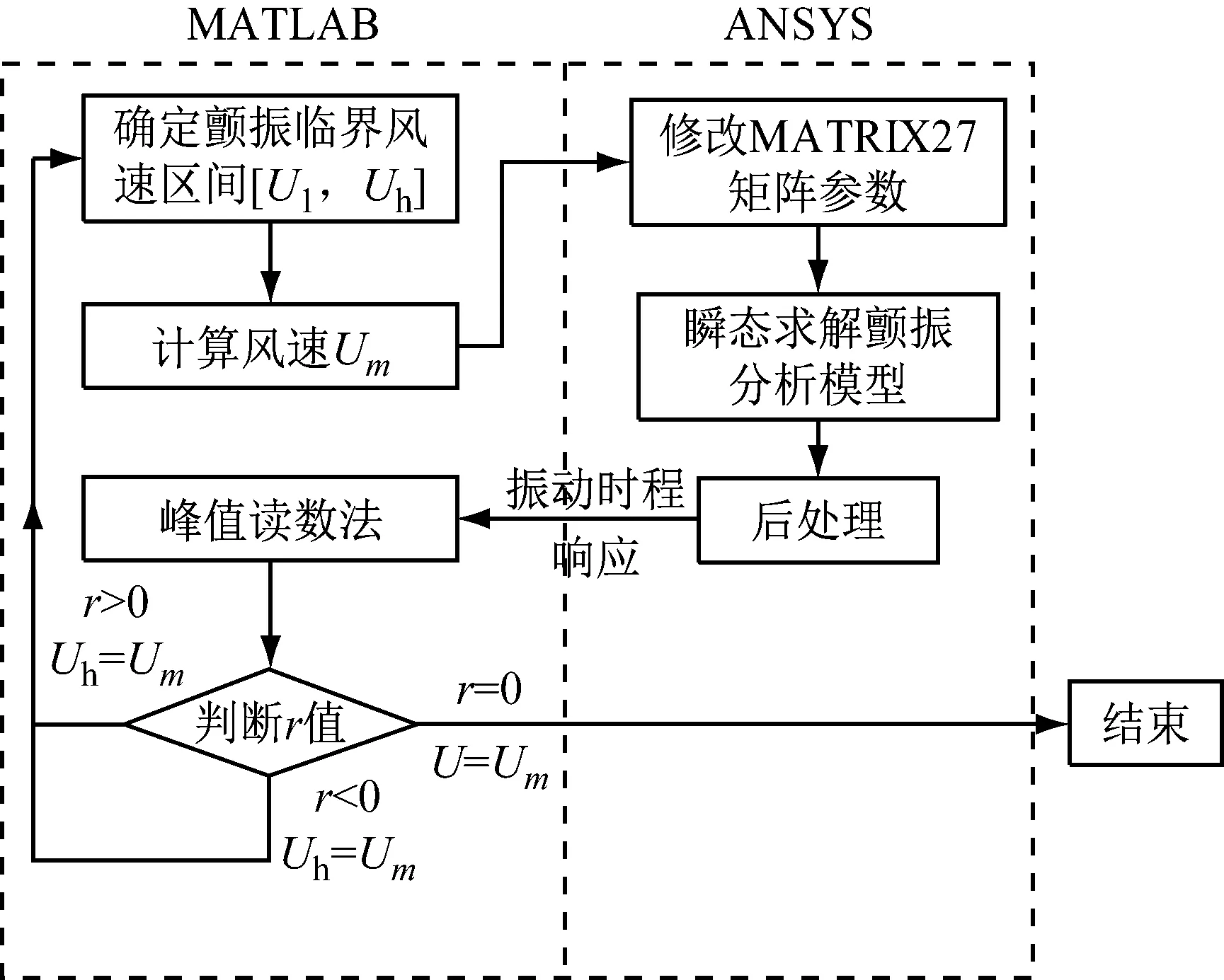
圖1 顫振時域分析實現框架Fig.1 The implementation framework of time-domain flutter analysis

3 算例驗證

3.1 理想平板斷面的簡支梁

為驗證所提時域自激力計算的準確性，以理想平板的顫振分析為例，并將計算結果和理論解對比分析。該簡支梁長度為300 m，橋面寬度40 m，材料彈性模量取2.1×1012Pa，橫向抗彎慣性取8.57 m4，豎向抗彎慣矩取1.0×104m4，扭轉慣矩取0.386 m4，質量取2×104kg/m，質量慣矩取4.5×106kg·m，空氣密度取1.225 kg/m3，簡支梁前10階的自振特性如表3所示，理想平板顫振導數如圖2所示。

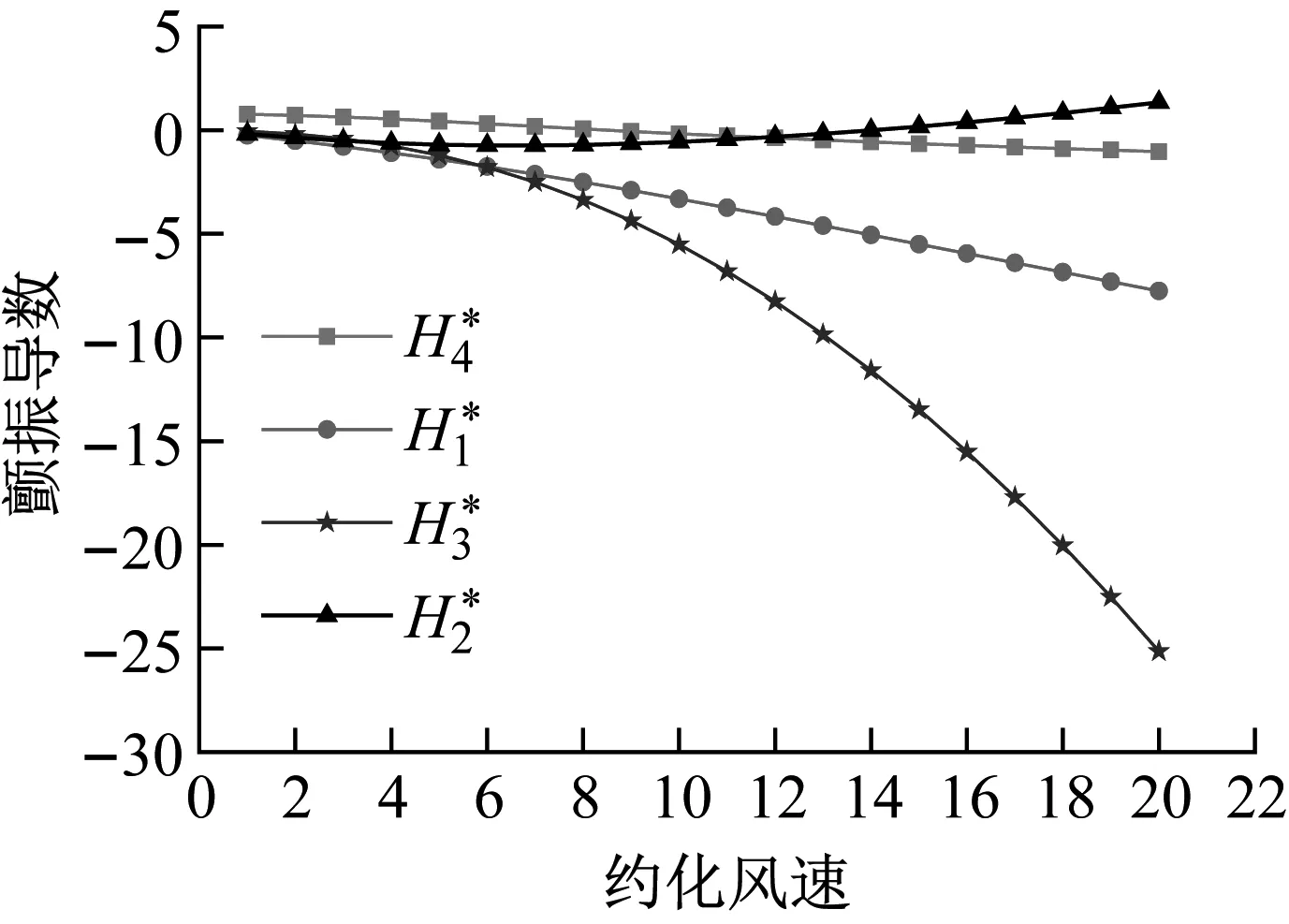
(a) H*

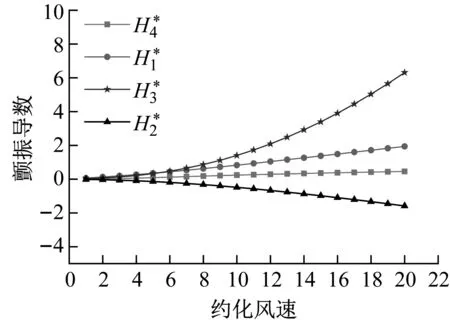
(b) A*圖2 理想平板的顫振導數Fig.2 Aerodynamic derivatives of ideal plate

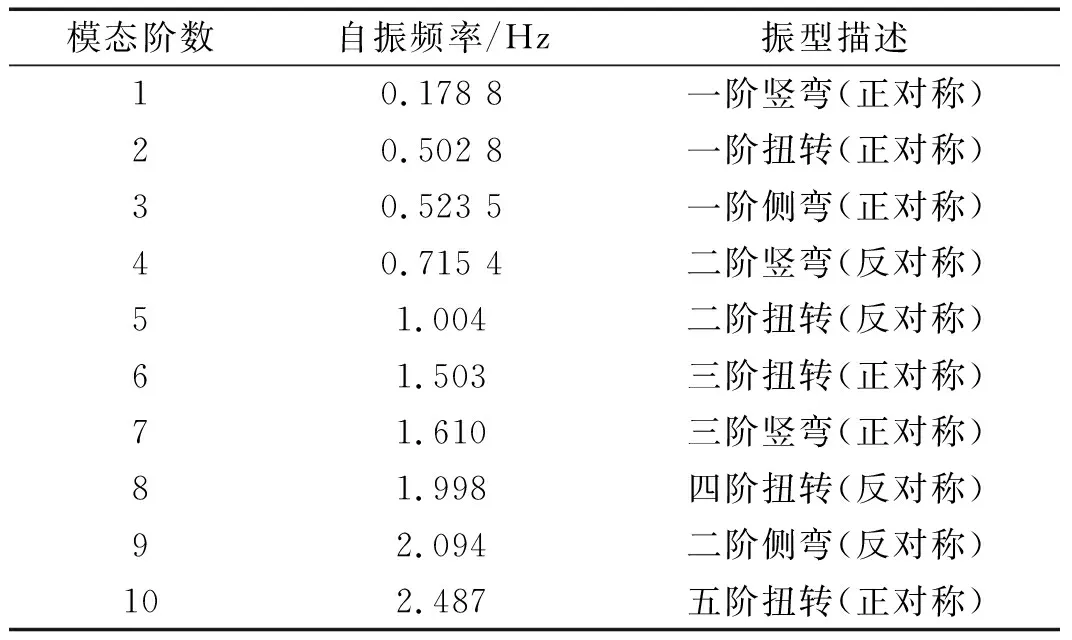
表3 簡支梁前10階自振特性Tab.3 The first ten order frequencies of simply supported beam bridge

在MATRIX27矩陣單元的顫振分析模型建立過程中，首先將簡支梁劃分為30個單元，將質量等效到節點上，梁端節點約束扭轉自由度，引入29個氣動剛度矩陣、29個氣動阻尼矩陣和29個氣動質量矩陣，顫振分析有限元模型如圖3所示，模型共包括單元210個，節點122個，基于擬牛頓+通用全局優化算法對理想平板顫振導數擬合后得到的氣動力系數如表4所示。

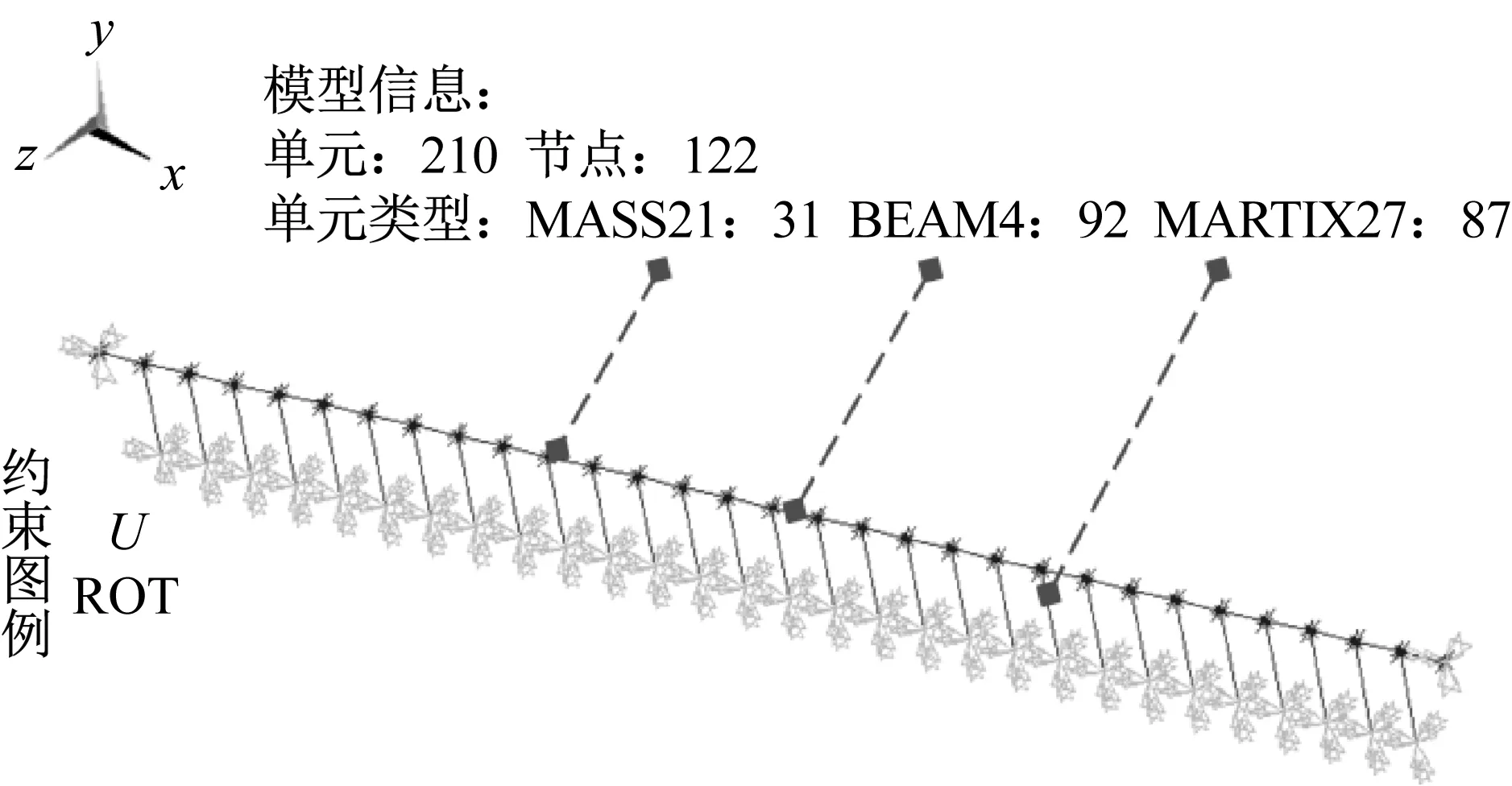
圖3 簡支梁顫振分析有限元模型Fig.3 Flutter analysis FE model of simply supported beam bridge

表4 理想平板氣動力系數Tab.4 Aerodynamic coefficients of ideal plate

從表4中可見：φlα和φmh的氣動質量項足夠小，可以忽略不計，而φlh和φmα的擬合值并非如此，因此，在進行氣動導數擬合時，不考慮氣動質量項可能使得擬合結果出現偏差，可能影響顫振臨界風速的計算結果。

簡支梁在顫振發生及前后時的跨中豎向位移和扭轉位移的響應時程如圖4所示，由圖可見：隨著風速的增加，簡支梁跨中位置振動時程曲線由衰減到逐步發散，在顫振臨界風速處，簡支梁維持等幅振動。

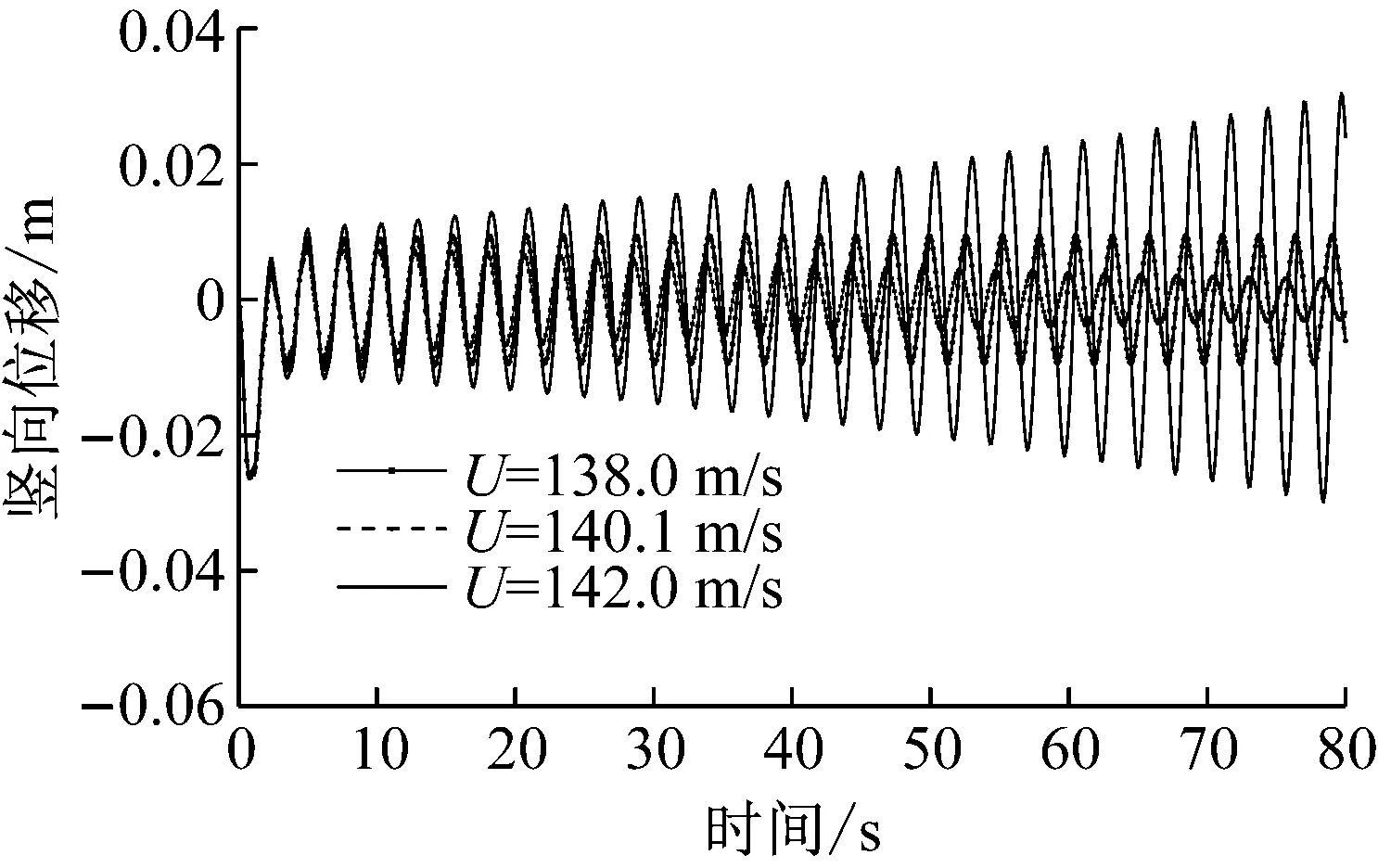
(a) 豎向位移時程

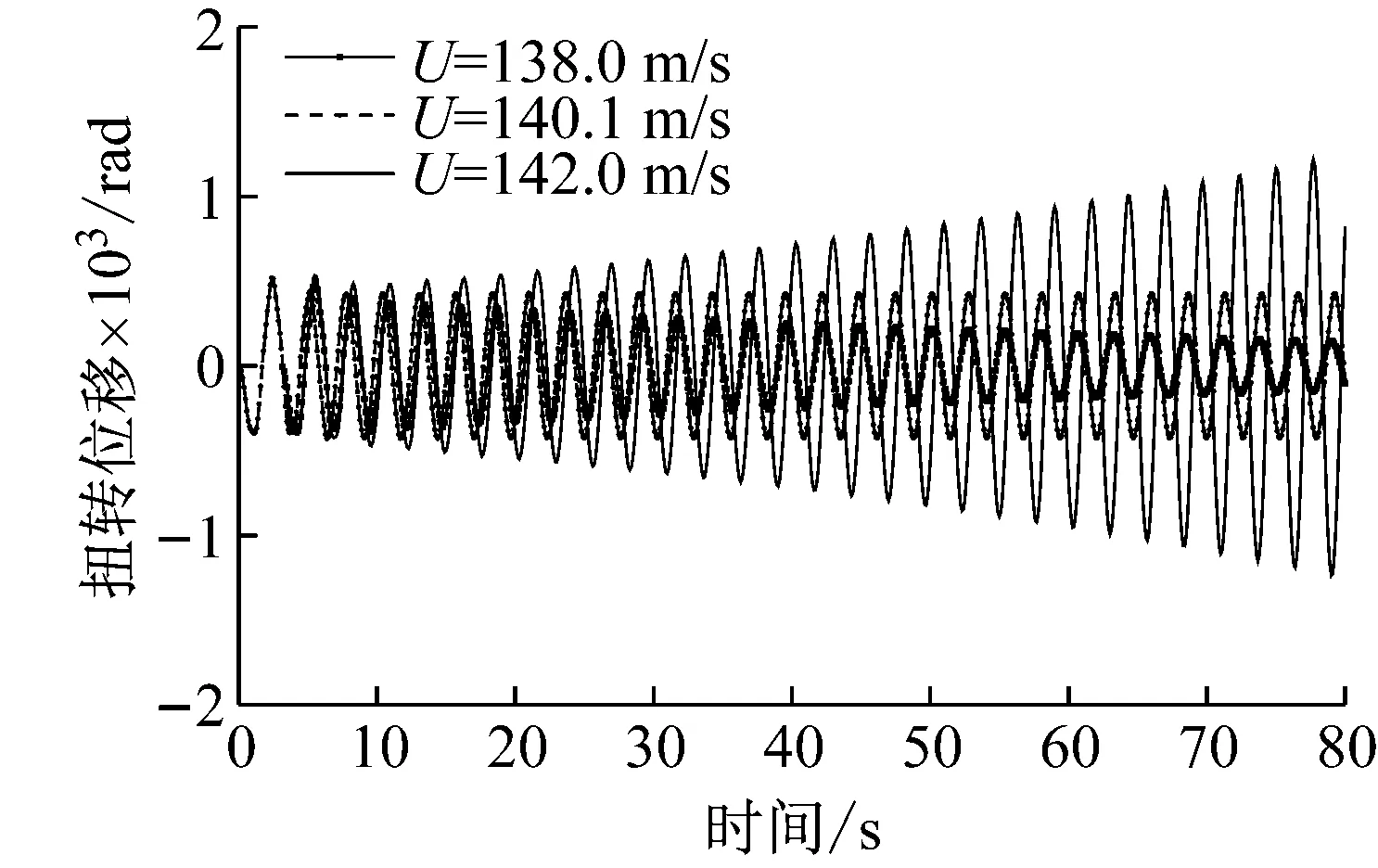
(b) 扭轉位移時程圖4 顫振前后簡支梁跨中位移響應Fig.4 Displacement responses of mid-span of simply supported beam bridge before and after flutter

表5為本文方法與其他方法計算結果的比較，由表可知：本文所提方法的計算結果與理論解吻合良好，誤差不足1%。

若不重新改寫非線性Φsel，直接由Newmark-β進行時程求解上述自激力模型時，則會出現文獻[9]中的結果，結構的顫振臨界風速值受時間步影響較大，這是由于計算時步的真實荷載受當前和上一時刻橋梁運動狀態共同的影響，直接遞推得到的自激力在相位差和大小上與實際值存在一定的差距。為研究時間步長對本文所提方法的影響程度，分別計算不同的時間步長下的顫振臨界風速值，計算結果如表6所示。由表6可知：對非線性Φsel處理后，時間步長的選取對顫振臨界風速的計算結果依賴性不明顯。

3.2 某大跨斜拉橋顫振臨界風速計算

以某大跨度斜拉橋顫振分析為例，設計采用三塔斜拉橋方案，橋梁跨徑具體布置為110 m+129 m+258 m+258 m+129 m+110 m，全長994 m，橋梁寬度為38.8 m，箱梁高為4.5 m，主梁標準斷面如圖5所示。

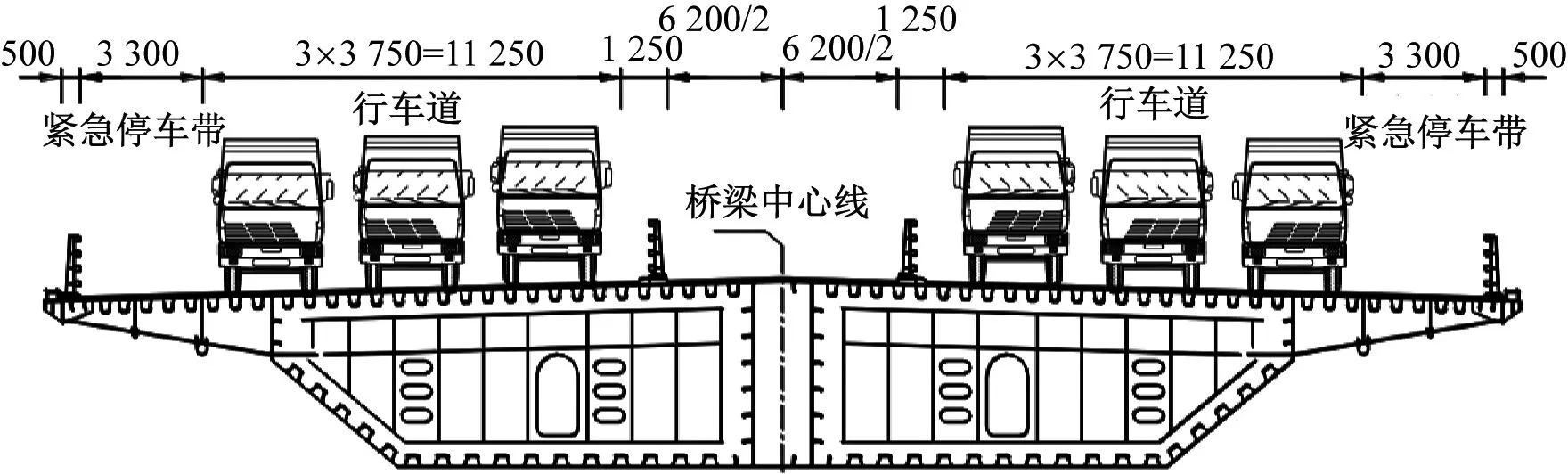
圖5 橋梁標準斷面(mm)Fig.5 Standard section of a bridge (mm)

圖6為該主梁斷面節段模型0°風攻角下的(幾何縮尺比為1∶50)顫振導數試驗及擬合結果(擬合值為無符號的曲線)，表7為氣動力系數計算結果。

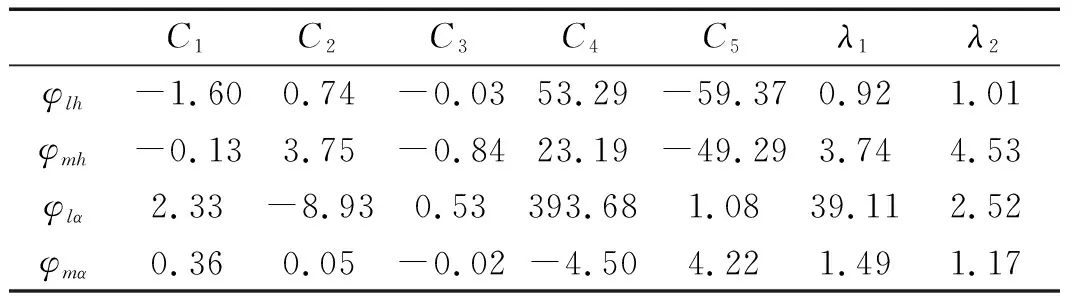
表7 橋梁斷面平板氣動力系數Tab.7 Aerodynamic coefficients of bridge section

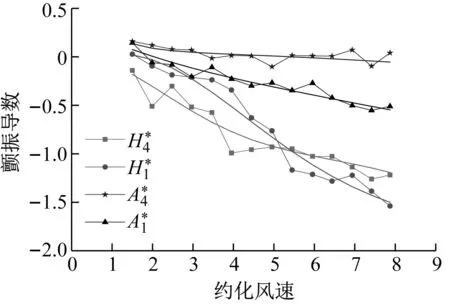
圖6 0°風攻角下的顫振導數和擬合結果Fig.6 Flutter derivatives and fitting results under 0° wind attack angle

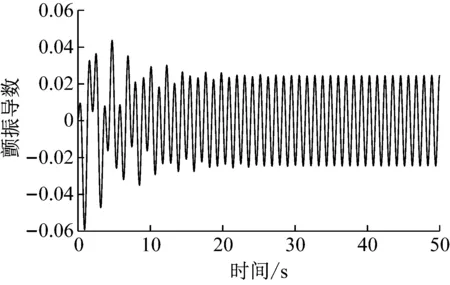
(a) 豎向位移時程

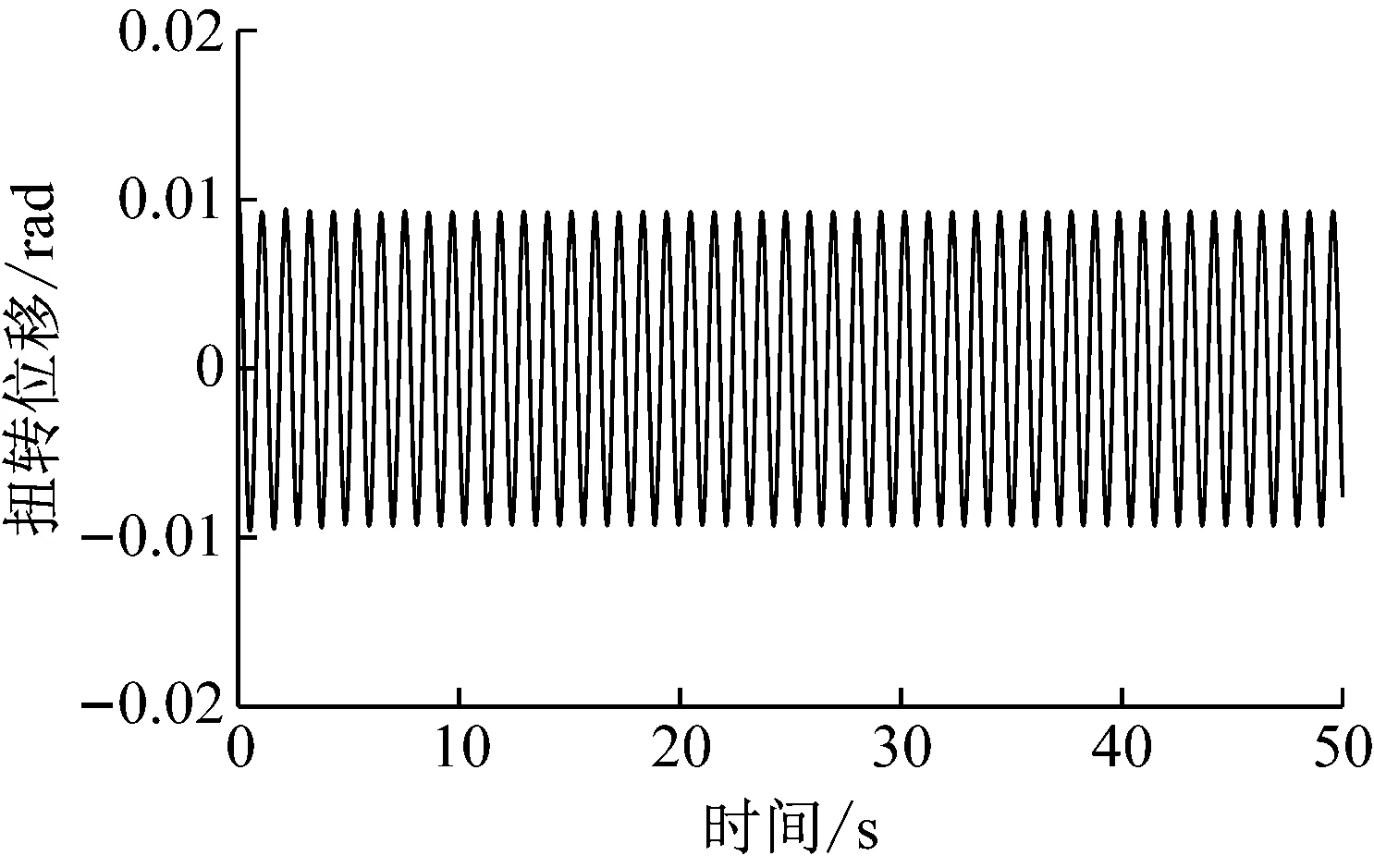
(b) 扭轉位移時程

0°風攻角下，試驗顫振臨界風速>17 m/s，換算實橋顫振臨界風速>110.5 m/s，通過本文方法計算得到顫振臨界風速Ucr=198.6 m/s，顫振臨界頻率fcr=0.930 8 Hz，遠高于成橋狀態顫振檢驗風速79.88 m/s，說明該橋的顫振穩定性良好。圖7為顫振臨界風速條件下橋梁主梁斷面豎向、扭轉位移響應時程曲線，可以直觀地判斷結構正處于臨界運動狀態。

4 結 論

(1) 基于自激力有理函數表達式，推導了時域自激力遞推計算過程，提出了一種基于ANSYS的橋梁顫振時域分析模型和求解方法，并采用MATLAB和ANSYS混合編程技術實現了顫振臨界風速的程序求解。

(2) 在相同約束條件的限定下，相比其他幾種優化算法，擬牛頓+通用全局優化算法在氣動力系數識別過程中迭代步數更少，收斂更快，擬合效果更好。

(3) 以經典平板顫振為例，采用本文所提方法計算得到的顫振臨界風速和顫振頻率與理論吻合度很高，并且本文所提方法對計算時間步長的選取不具備依賴性，某大跨橋梁顫振臨界風速計算說明所提方法在工程應用中具備實用性和可操作性。

(4) 伴隨著橋梁抗風精細化研究的進程，結合通用有限元程序在處理非線性問題上優勢，本文所提方法為復雜的非線性顫振問題研究分析提供了參考。