多傳感器數據融合的復雜系統退化模式挖掘
彭宅銘, 程龍生, 姚啟峰
(1.江蘇科技大學 經濟管理學院,江蘇 鎮江 212100;2.南京理工大學 經濟管理學院,南京 210094)
隨著復雜性、綜合性和智能化水平的日益提升,現代裝備系統逐漸發展成為具有更長壽命和更高可靠性的大規模復雜系統。由于系統結構復雜,各功能模塊相互作用、相互依賴,關鍵部件的故障可能導致整個系統停止運行,給用戶帶來巨大的經濟損失。復雜系統故障預測與健康管理(prognostics and health management, PHM)技術就是針對大型高價值復雜系統的自主保障、自主診斷的要求提出來的,該技術可利用先進的傳感器獲取系統運行狀態信息,借助智能推理算法,實現系統狀態的分析與監控、診斷與預測評估,對降低系統的維修成本、提高安全性與可靠性具有重要的意義[1]。退化模式挖掘是PHM技術的主要內容之一,該技術基于裝備或系統的歷史數據來構建狀態評估模型,以此掌握不同環境下系統退化或降級的規律,挖掘可能存在的退化或降級模式,搭建全面的系統退化模式庫。由于歷史數據往往呈現時序性、高維性、復雜性、高噪聲等特性,如果將其直接用于退化模式挖掘,不但在儲存和計算上要花費高昂代價,而且可能會影響算法的準確性和可靠性。因此,有效的建立退化模式的方法就是對歷史數據進行時間序列數據挖掘[2]。一方面,在降維或融合算法的基礎上構建健康狀態評估模型,以健康指數(health indicator,HI)曲線刻畫系統的變化趨勢;另一方面,利用時間序列聚類算法開展退化模式挖掘研究,探索不同的衰退模式。
復雜系統健康狀態評估方法層出不窮,從HI構建的策略可以分為基于物理特征的健康指數(physics HI,PHI)方法和基于融合特征的健康指數(fusion HI,FHI)方法兩類[3]。PHI方法主要使用統計方法或信號處理技術從監測信號中提取物理特征作為監測指標,如均方根、峰值、頻譜特征和能量等。但這些PHI僅對特定性能退化階段中特定故障敏感,無法滿足系統全面健康狀態監測的敏感性和穩定性。于是,在此基礎上開發出了FHI方法,通過融合多個PHI或多傳感器信號來構造表征系統健康狀態和退化程度的參數。主成分分析法(PCA)能夠在減少特征維數的同時保留盡可能多的信息,在FHI方法中也得到了大量的應用[4-6]。但是,PCA選擇的主成分的物理特性往往難以解釋。此外,特征融合方法,如神經網絡[7]、遺傳算法[8]、隱馬爾可夫模型[9]、支持向量機[10]等方法也被廣泛使用到FHI的構建中。這些算法的實用性在實踐中都得到了驗證,但無法描述特征對系統故障的敏感性和重要程度。馬氏距離(Mahalanobis distance,MD)作為一種無量綱、尺度化的協方差距離,能夠量化不同類別數據之間的差異,在構建FHI時表現出了較為理想的效果[11-12]。馬田系統(Mahalanobis-Taguchi system,MTS)方法[13]是Taguchi提出的一種結合MD和質量工程學的多維模式識別方法,該算法可以在使用較小的樣本量且沒有任何先驗信息的情況下,輕松地測量數據的異常程度并提供準確的結果。相比其它的特征融合算法,MTS不僅使用MD將所有相關信息融合為一個度量標準,而且能夠識別出對故障信息敏感的特征。因此,MTS成為了當前部件或系統PHM的有效工具之一[14-15]。
時間序列聚類算法的主要過程是距離度量和聚類。在距離度量過程中,可選擇多種不同的距離度量方法,如MD、歐式距離(Euclidean distance,ED)和動態時間彎曲(dynamic time warping,DTW)距離等[16]。相比MD和ED,DTW克服了點對點的缺陷,通過彎曲時間來測量長度不等的時間序列數據,能夠實現數據點一對多匹配。因此,這種距離度量對時間偏差和幅度改變具有更強的穩健性[17]。在聚類算法選擇上,層次聚類算法不僅不需要預先制定聚類數,而且能通過聚類結果準確描述整個聚類過程。因此,可利用DTW距離和層次聚類算法有效地挖掘滾動軸承的衰退模式[18]。
基于此,本文提出一種基于多傳感器數據融合方法的復雜系統退化模式挖掘方法,通過改進MTS算法構建融合健康指數,利用分段點分析方法和基于DTW的層次聚類算法挖掘系統的不同退化模式,并利用航空發動機實例來驗證所提方法的有效性。該方法充分利用現有系統全壽命周期數據,對系統衰退模式進行挖掘,為系統在線監測和剩余壽命預測提供依據,具有一定的理論價值和應用價值。
1 多傳感器特征融合技術
復雜系統不同部件(或子系統)的傳感器數據能夠真實反映其性能狀態,是其健康評估的基礎。隨著系統復雜程度的不斷提升,數據維度也成倍增長,為在線評估和預測帶來了挑戰。根據PHM的內容,在對復雜系統進行健康狀態評估前,需要通過數據采集、特征提取和特征選擇等過程來提取有利故障特征,構建評估矩陣,基于評估矩陣構建健康狀態評估模型,以此來量化評估系統的健康水平。
MTS將MD與質量工程學中的正交表(OA)和信噪比(SNR)相結合,實現多維特征的篩選和融合。同時,得到的MD是一種協方差距離,可以通過計算樣本與樣本集“重心”的最近距離來量化兩個樣本的差異。但是,在實際操作中MTS方法也存在明顯不足:在基準空間優化時利用OA和SNR篩選的特征子集未必是最好的[19]。為此,本文提出改進MTS(improved MTS,IMTS)算法,并將其運用到多傳感器數據的降維和融合中,以此來構建FHI。
1.1 基于IMTS的退化參數篩選與融合
基于IMTS的退化參數篩選與融合過程主要有四個階段,具體如下:
階段1基準空間(MS)構建
該階段是IMTS的基礎,需要從連續的時間序列數據中區分出“正常樣本”和“異常樣本”,確定“正常樣本”和計算MD值。
(1) 按照性能參數的退化程度進行樣本選擇,早期的T0個監測數據作為“正常樣本”,末期T1監測數據作為“異常樣本”;
(2) 計算“正常樣本”的MD值。設xi(i=1,2,…,n)為n個包含p個變量的樣品,xi=(xi1,xi2,…,xip),xij為第i個樣本的第j個變量的觀測值,則第i個樣品的馬氏距離平方(簡稱馬氏距離)為
(1)
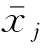
階段2基準空間有效性驗證
在基準空間優化之前要對上一階段構建的基準空間的有效性進行驗證。
階段3基準空間優化
Taguchi認為并非所有的特征對分類都有貢獻,有些變量可能會產生冗余信息、增加計算的成本和復雜度,因此,需要對原始變量進行篩選,挑選出其中的重要特征作為分類依據。
ReliefF算法是Kononenko[20]于1994年提出的基于特征權重的特征選擇算法。通過搜索當前樣本的各種近鄰,綜合計算特征權重,將權重小于閾值的特征移除,以選擇最優特征子集。該算法計算簡單,易于理解,在分類問題的特征選擇中具有獨特優勢。為此,本文使用ReliefF算法代替OAs和SNR方法優化基準空間。但是,在實際運用中發現,利用ReliefF算法選擇的特征之間可能存在高相關性,出現特征冗余,導致式(1)中的S不可逆,使得MD值無法計算。因此,如果能在進行ReliefF選擇之前消除特征之間的相關性,將會有效地解決此類問題。基于以上的理論和實踐,提出基于相關性聚類和ReliefF算法的兩階段特征選擇算法來優化基準空間,具體步驟如下:
(4) 分別計算特征之間相關性系數的絕對值rij,得到相關系數矩陣r;
(5) 根據r進行特征聚類,將特征相關性大于閾值δ1的特征聚為一類,得到k類特征子集;
(6) 利用ReliefF算法計算所有特征的權重Wj并選擇每一類中權重最大的特征構成特征子集FS1;
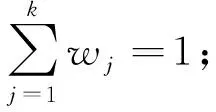
在上述過程中,步驟(5)和(6)利用相關系數聚類,可以消除特征集的高冗余性。本文選取Person相關系數,當其絕對值在0.8以上,認為特征間有強的相關性。因此,本文δ1選擇在0.8~1.0之間。步驟(8)中的Sp類似于PCA中的累計貢獻率,當Sp>δ2時可認為選擇的特征子集可以解釋原有的特征集,類似地,本文取δ2在0.85~1.0之間。
階段4樣本馬氏距離計算
優化后的基準空間中包含初始特征集中的重要特征,可以利用其計算各樣本的MD值。
(9) 利用優化后的基準空間計算樣本的MD值:
(2)
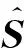
以上的IMTS方法操作簡單,在降維時保持了特征集的分類能力,大大降低算法的復雜度。另外,利用該算法計算出的MD也是一種有效的刻畫樣本差異性的工具,可以作為表征系統性能狀態的參數。
1.2 基于優化MD的健康指數構建
單一時刻的MD只能刻畫系統偏離正常狀態的程度,不能很好的反映該系統的健康狀態變化過程,因此需要結合時間信息來獲取相應的MD時間序列,以此來描述系統的退化過程及隨時間偏移的程度。事實上,系統的健康狀態遵循單調性原則,即如果沒有進行人工干預(例如維修),系統的健康狀態不會隨時間推移而改善,也不會突然出現大幅度下降(例如,從90%突然降到20%)。因此,需要根據單調性原則來計算HI,從而可以準確反映系統健康狀況。
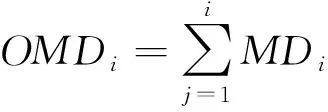
(3)
式中,OMDmin和OMDmax分別為系統全壽命周期樣本計算的OMDi的最小值和最大值。
由式(3)可知,HIi∈[0,1],且單調遞減,值越大,系統越健康。系統整個壽命周期的HI曲線會呈現明顯的變化趨勢(如圖1)。在整個過程中,曲線斜率均為負值,當系統處于穩定階段時,曲線趨近于直線,而當系統逐漸退化,到達一定的閾值之后,曲線的斜率不斷減小,直到HIi趨近于0。因此,通過以上方法定義的健康指數將有利于退化分段點確定。
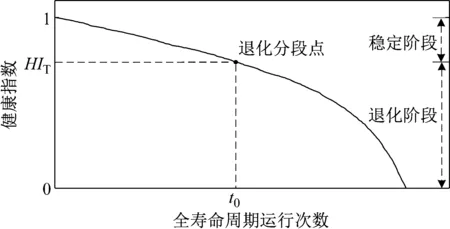
圖1 分段性能退化過程Fig.1 Piecewise performance degradation process
2 DTW層次聚類退化模式挖掘
2.1 退化分段點確定
假設某一系統全壽命周期共存在n個循環,其HI值記為H={h1,h2,…,hn},對應的HI曲線圖如圖1所示。根據第1.2節的定義可知,HI存在圖1中的退化分段點,該分段點的確定對于退化模式挖掘具有重要價值。
CUSUM(cumulative sum)算法是一種序貫分析技術,可以通過累積作用,將退化過程中的微小波動通過累計偏差反映出來,從而可以準確檢測出退化分段點。CUSUM算法步驟如下:
(2) 令S0=0,計算累計和Sj:
(4)
(3) 尋找累積和Sj的極值點,即為退化分段點。
2.2 退化模式庫構建
通過計算訓練集樣本的健康指數,建立健康指數曲線集合C={C1,C2,…,CN}。這些曲線記錄了同一類型設備在不同環境中的運行狀態,雖然各不相同,但存在具有類似退化趨勢的樣本。因此,有必要對健康指數曲線進行聚類分析,構建退化模式庫。
DTW距離在計算時不要求兩條時間序列具有相等的長度,可實現異步相似性比較,同時,對異常點不敏感。因此,DTW距離可以很好的作為健康指數曲線相似性度量的標準。層次聚類算法不需要預先設定聚類數,通過計算數據集樣本間的相似性,不斷的將相似性最高的樣本合并構成新的集群,直到所有樣本聚為一類。該算法的優勢就在于可以表征聚類的全過程,同時可以清楚地知道各類之間的距離關系。為此,本文將利用DTW距離度量的層次聚類算法來挖掘系統的退化模式。具體步驟如下:
(1) 利用CUSUM算法確定N個健康指數曲線的分段點,并將退化階段的健康指數曲線構成退化曲線集合D={D1,D2,…,DN};
(2) 將單個退化曲線Di視為一類,計算Di和Dj之間的DTW距離dij,得到初始距離矩陣;
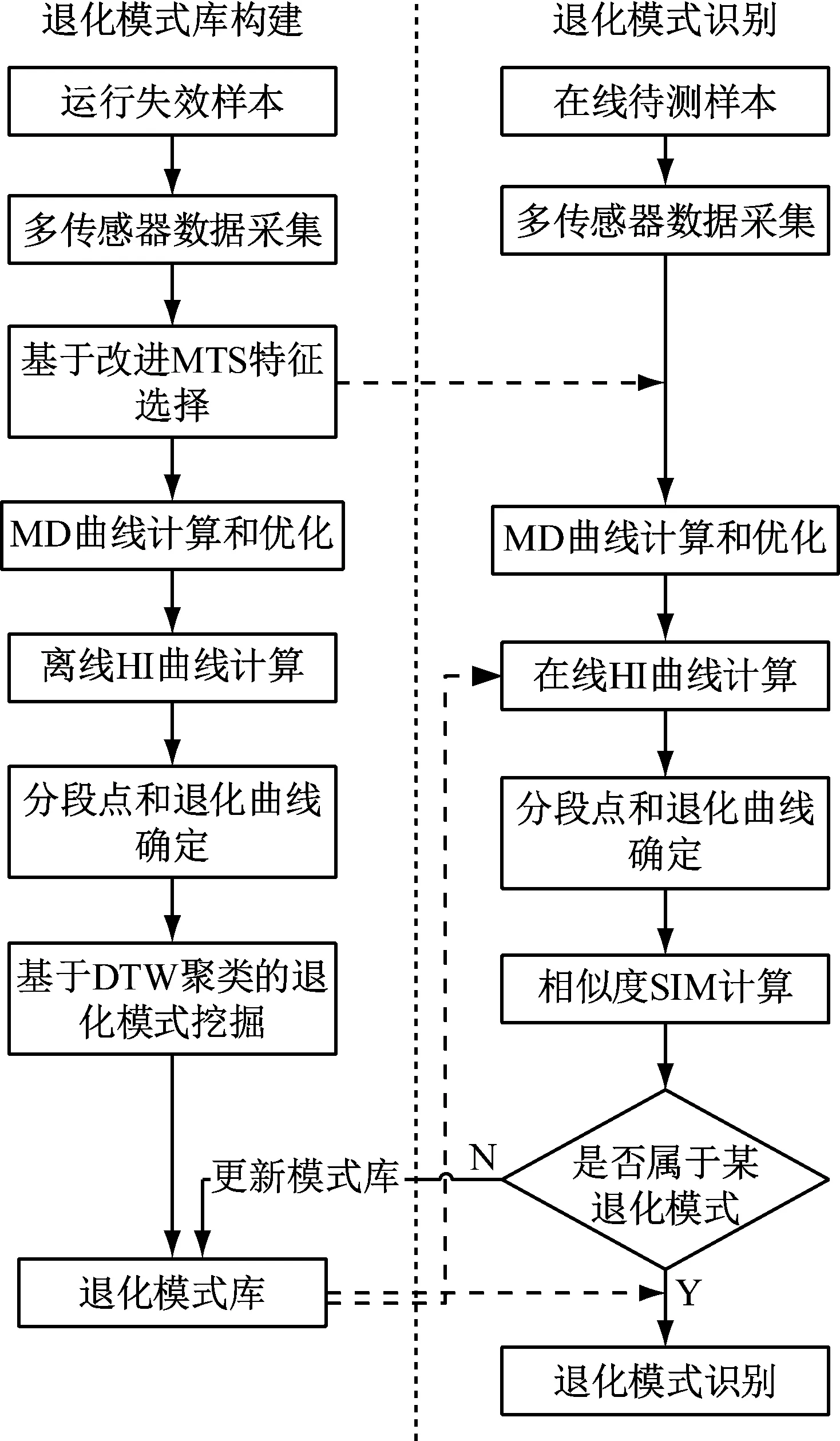
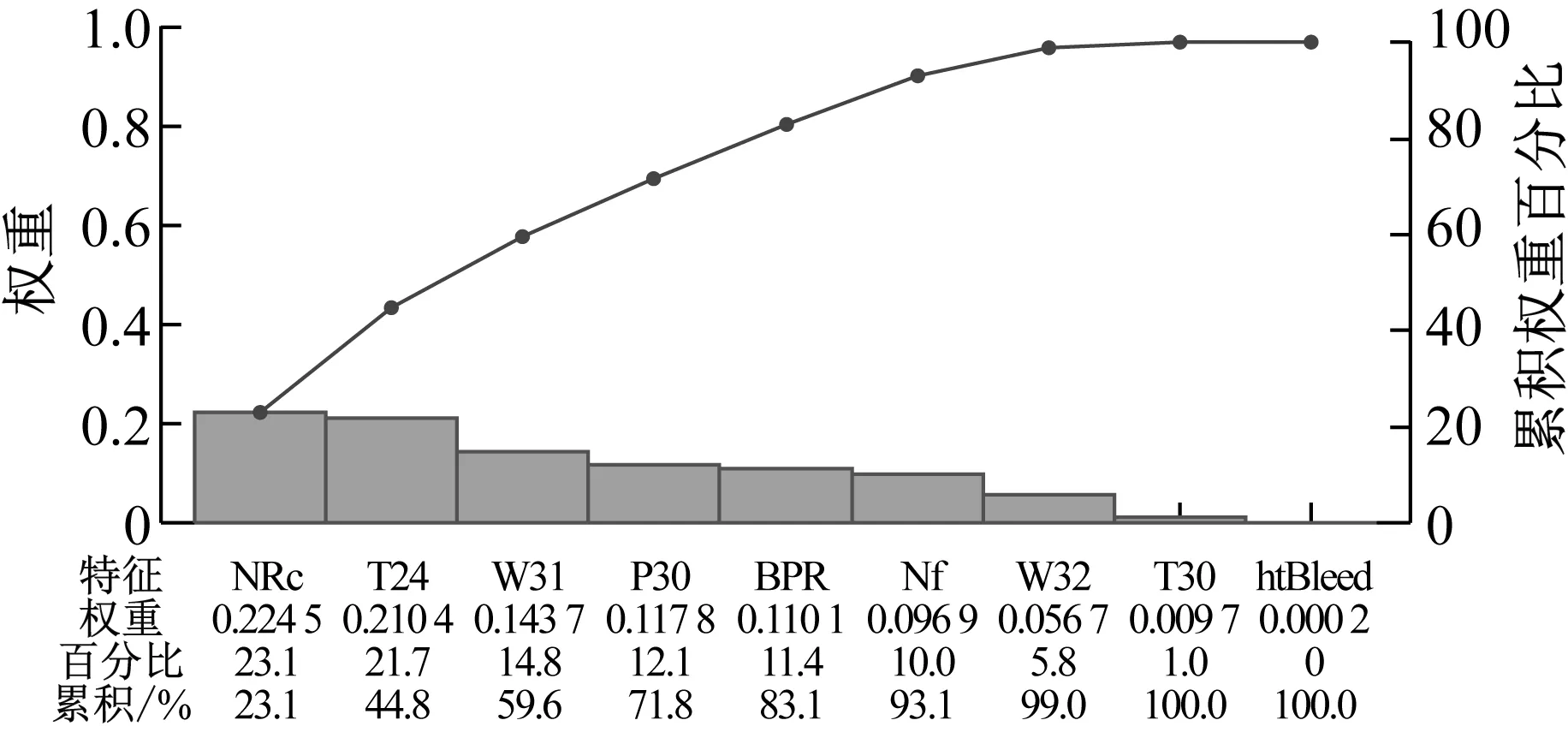
(3) 將初始距離矩陣中距離值及對應的退化曲線存放在數組DS={(Di,Dj,dij)|1≤i (4) 將DS中dij最小的值對應的兩條退化曲線合并為一類,形成新的聚類; (5) 從DS中刪除對應的類和距離值,計算新聚類與其它類之間的距離,更新距離矩陣; (6) 重復步驟(3)~(5),直到全部聚為一類; (7) 根據設定的終止條件確定聚類數目k和聚類結果。 為更好地刻畫新的聚類與其它類之間的特征,將新的聚類中所有樣本到其它類之間距離的平均值作為類間距離。由于層次聚類的最終結果不是單一聚類,而是一個聚類層次,選擇不同的終止條件將產生不同聚類數目。因此,選擇一個合適的終止條件對聚類的結果有很大的影響。本文將根據類內相似度和退化時間區間確定不同類之間的閾值。 基于相似度的退化模式識別的基本思想是找到與測試樣本具有最高相似性的退化模式。對待測樣本Y=[y1,y2,…,ym]T,yi=(yi1,yi2,…,yip)為第i個周期的特征數據,其退化模式識別步驟和流程如下: (1) 利用IMTS優化的基準空間計算待測樣本從開始運行到當前周期的MD值和MD累計和OMDi; (2) 利用式(3)計算各時刻的健康指數HIi,得到HY=[HI1,HI2,…,HIm]T,其中OMDmin和OMDmax使用退化模式庫中各模式樣本的OMDmin最小值和OMDmax最大值; (3) 根據退化模式庫中的退化閾值確定Y的退化曲線DY; (4) 計算DY與各退化模式Ci的相似度: (5) 式中:Sim(Ci,j)為DY與Ci中每一條退化曲線D(j)的DTW距離;ni為模式Ci中退化曲線個數。 (5) 根據SIM(Ci)值和退化模式Ci的退化時間區間來確定Y所屬的退化模式。模式Ci的退化時間區間定義為DTCi=[min(TCi),max(TCi)],其中TCi為模式Ci中樣本的退化時間,min(TCi)和max(TCi)分別為模式Ci中樣本退化時間的最小值和最大值。假設測試樣本Y所經歷的退化時間為T,DY與模式Ci的相似度為SIM(Ci),i=1,2,…,l,將其按照從小到大排序為:SIM(Ck1) ①若T∈DTCk1,則Y屬于模式Ck1; ②若T?DTCk1,則Y不屬于模式Ck1,進而判斷T是否在DTCk2,若T∈DTCk2,則Y屬于模式Ck2;以此類推,直到T在某一模式的退化時間區間內,則將其歸為該類模式。 ③若T不是任何一種模式的退化時間區間內,則將Y單獨作為一類新的退化模式。 退化模式庫的構建是一個不斷學習的過程,在確定某樣本的退化模式后,可將其加入相應的退化模式,更新模式庫,以便更準確識別其他測試樣本。退化模式識別的具體流程如圖2所示。 圖2 退化模式識別流程Fig.2 Flowchart of degradation pattern recognition 航空發動機是一個復雜的機電液磁耦合系統,其性能退化并不決定于某一個變量的退化,而是多個狀態變量動態變化且相互耦合的結果,如溫度、電壓、振動等,所以必須充分利用多個傳感器的特征參數,從中提取能體現系統退化特性的特征參數,才能準確了解航空發電機的退化狀態。本文對美國國家航空航天局(NASA)提供的航空發動機全壽命周期退化仿真數據進行分析,該仿真數據是借助商用模塊化航空推進器軟件(C-MPASS)獲得的。通過改變輸入參數模擬風扇、高壓渦輪、低壓渦輪、高壓壓氣機和低壓壓氣機的故障和性能退化過程,利用傳感器記錄反映航空發動機運行狀況的21個監測參數,其中包括低壓壓縮機出口溫度(T24)、高壓壓縮機入口溫度(T30)、高壓壓縮機出口壓力(P30)、風扇物理轉速(Nf)、核心機轉速(NRc)、涵道比(BPR)、高壓渦輪冷卻引氣流量(W31)、低壓渦輪冷卻引氣流量(W32)和引氣焓值(htBleed)等[21]。不同性能監測參數與航空發動機的退化狀態有不同的相關性,根據訓練集所有參數的散點圖和局部加權回歸(LOESS)散點平滑法選擇有明顯變化趨勢的14 個參數構建航空發動機的狀態矩陣。 本文選取FD001數據集,該數據集包含100個訓練集樣本,可作為歷史數據進行退化模式挖掘。為驗證方法的有效性和穩定性,利用5折交叉驗證,隨機選擇其中的80個樣本作為測試集,剩余20個樣本作為測試集。以其中的一次交叉驗證為例,介紹退化模式挖掘的流程,具體如下: 首先利用IMTS對歷史樣本數據進行分析,篩選對退化有利的特征。為消除發動機初期不穩定帶來的影響,選取訓練集中發動機的第6-10個周期飛行的數據作為正常樣本,最終運行的5個周期飛行的數據作為異常樣本,各包含500個樣本。選擇有變化趨勢的參數構建航空發動機的評估矩陣。基準空間有效性驗證結果顯示,超過98.8%的正常樣本的MD值小于異常樣本的MD值的最小值,說明所建立的基準空間是有效的。利用特征之間的相關性,按照第1.1節進行特征聚類,取δ1=0.9。利用ReliefF算法計算特征的權重,并選擇每一類中權重最大的特征構建特征子集,得到9個特征,將其按照標準化權重從大到小的順序排列,如圖3所示。 圖3 特征的權重占比Fig.3 The weight ratio of each feature 由圖可知,前6個特征的累積權重已經達到了93%,因此,選擇NRc、T24、W31、P30、BPR、Nf構建優化基準空間。 分別計算訓練集樣本的全壽命周期的MD值和HI。利用CUSUM方法獲取每個編號發動機的退化分段點和退化曲線。結果顯示,航空發動機的退化閾值HIi0集中在0.6~0.9之間。結合航空發動機退化特性,取平均值HI0=0.745 0作為該類型發動機的退化閾值,即當健康指數大于0.745 0時,發動機緩慢退化,處于穩定階段;當健康指數小于0.745 0時,發動機加速退化,處于退化階段,直至完全失效。 根據退化閾值和健康指數曲線,確定發動機的退化曲線,如圖4所示。 圖4 發動機退化曲線圖Fig.4 Degradation curve of engines 按照DTW層次聚類的步驟,得到如圖5所示的聚類譜系圖。聚類數目的選取對模式識別的準確率具有重要意義,本文基于以下三個原則來確定最佳聚類數目:①保證各類樣本具有較高的類內相似性;②要求各退化模式得到的退化時間區間盡量不重疊;③各模式樣本退化時間在剩余壽命預測允許的正向和負向預測誤差(10和-13)內。經過多次試驗,選擇類內相似度閾值為85%,最終選擇聚類數目為7,得到如表1所示的模式分類結果。分別選取各模式的樣本和退化循環次數進行對比,如圖6所示。 圖5 DTW分層聚類譜系圖Fig.5 Dendrogram of DTW hierarchical clustering (a) 不同模式退化曲線對比 (b) 不同模式退化循環次數對比圖6 不同退化模式對比Fig.6 Comparison of different degradation modes 表1 基于DTW聚類的模式聚類結果Tab.1 Model clustering results based on DTW clustering 由圖6(a)可知,各模式的退化趨勢有明顯的差異。從表1中可以看出,不同退化模式經歷的退化時間區間存在少量的重疊區域(模式四和模式五、模式五和模式六),但從圖6(b)中線箱圖可以看出,不同模式的退化時間存在明顯的差異。因此,可以利用得到的聚類結果和退化時間區間建立全面的系統退化模式庫。 最后,利用建立的退化模式庫和退化模式識別方法,對待測樣本進行識別,識別結果如表2所示。 表2 模式識別結果Tab.2 Model recognition results 為度量模式識別的準確性,評估所有測試樣本中正確識別的百分比,借鑒文獻[21]中的準確率計算公式,構造如下的準確率計算公式 (6) 式中:N為待測樣本個數;Cor(ei)表示識別結果,當識別的樣本的退化時間在對應的模式區間內時,說明預測正確,此時Cor(ei)=1,反之Cor(ei)=0。 通過計算可知,除了一個樣本被錯誤識別到模式七以外,剩余樣本的識別準確率為100%。通過對比該樣本退化曲線,該樣本的退化時間不在任何一類中,因此,可將其歸為單獨一類。 為驗證本文方法的穩定性,利用5折交叉驗證,得到如表3所示的結果。結果顯示,得到的模式數較為穩定,準確率較高,除了第1和第3次交叉驗證出現的新模式被誤識別外,其他測試樣本均識別準確。因此,本文的退化模式聚類和識別方法是有效的,可以將其作為剩余壽命預測的依據。 表3 交叉驗證結果Tab.3 Cross-validation results 為驗證本文方法的在退化模式挖掘中的優勢,選擇文獻[18]中的方法從健康指數構建和退化模式聚類兩個層面進行對比。在健康指數構建方面,本文利用MD累計和構建的健康指數具有單調性,而且可以準確區分出穩定階段和退化階段,而文獻中選擇信號的時域特征作為退化趨勢,不單調,且較難識別故障點。在退化模式聚類方面,航空發動機退化模式只與退化過程相關,本文利用退化曲線進行DTW聚類,而文獻則使用整個壽命周期退化趨勢進行DTW分段聚合,相比起來,本文方法更簡便、合理。 本文針對復雜系統的退化模式挖掘方法進行了研究,提出了基于IMTS的復雜系統健康狀態評估方法和基于DTW層次聚類算法的退化模式挖掘過程,通過NASA 提供的航空發電機的全壽命周期內的性能監測數據,驗證所提方法的有效性,得到以下結論: (1) 本文所提的改進MTS方法有效地解決了MTS中基準空間優化過程的不足,在復雜系統的健康評估時不僅能夠降低復雜系統監測數據的維度與冗余性,還能融合多傳感器數據構建MD度量,為構建合理的健康指數提供可能。 (2) 本文提出的基于DTW層次聚類的退化模式挖掘算法可以構建系統全面的退化模式庫,并準確識別出待測樣本的退化模式,能夠為復雜系統剩余壽命預測提供依據。3.3 基于相似度的退化模式識別
3 實驗與分析
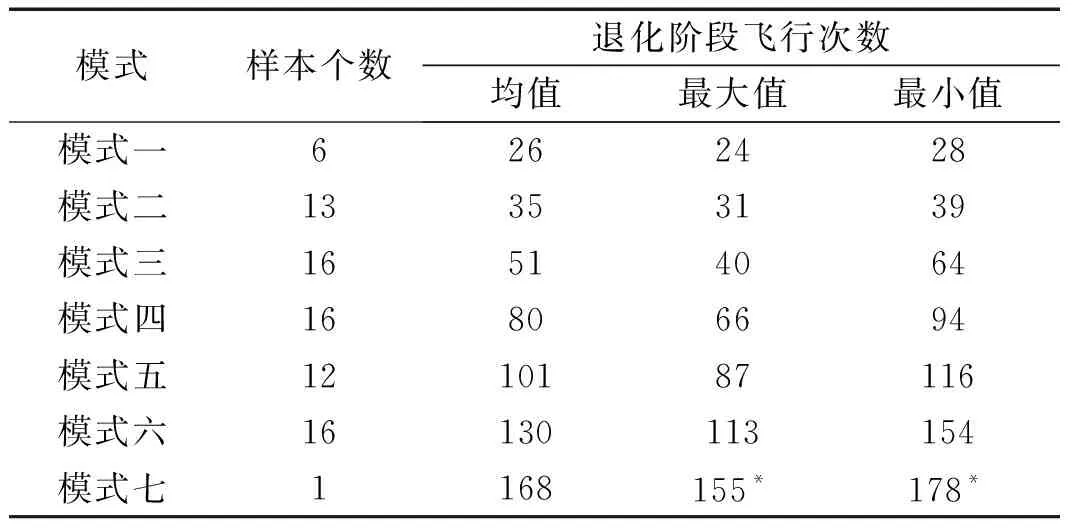
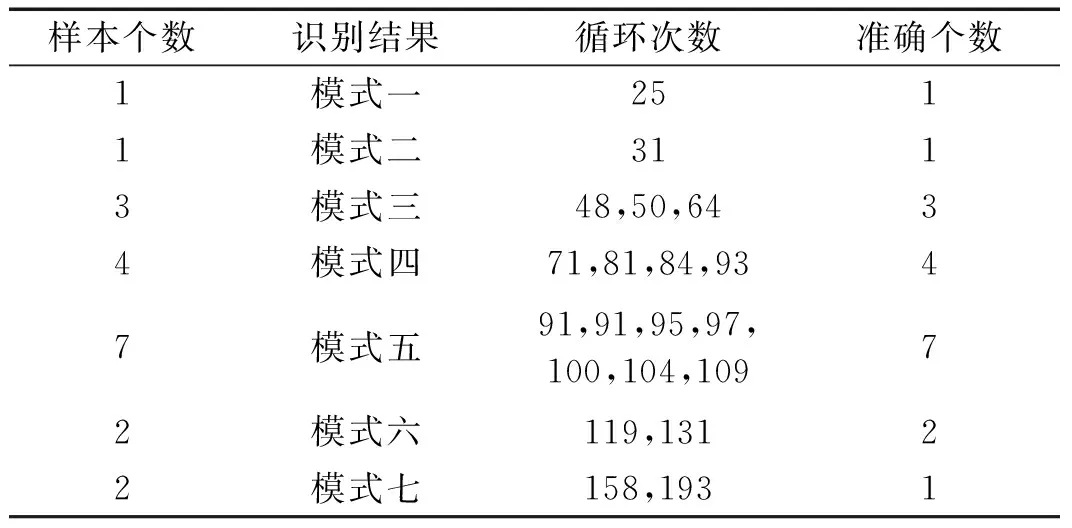

4 結 論

