分布式聲學黑洞浮筏系統隔振性能研究

趙 楠， 王 禹， 陳 林， 龐福振

(1.駐上海地區第八軍事代表室，上海 200011； 2.中國船舶及海洋工程設計研究院，上海 200011;3.哈爾濱工程大學 船舶工程學院，哈爾濱 150001)

聲學黑洞(acoustic black hole，ABH)是近年來新興的減振降噪技術，其結構特點為厚度h與距離尖端的距離x符合h(x)=εxm(m≥2)的函數關系，其功能特點為彎曲波在結構尖端聚集，波長逐漸減小并趨近于0，發生尖端無反射現象[1-2]，從而降低彎曲波在結構中的傳遞，實現減振降噪的目的。

目前，已有大量學者對聲學黑洞結構做出相關研究[3-6]；何璞等[7]基于一維聲學黑洞原理，提出聲學黑洞盒式結構，并利用有限元分析方法探究了該結構的振動特性，研究表明聲學黑洞盒式結構對振動峰值具有5～30 dB的削減作用；郭浩[8]提出一維聲學黑洞桿結構，并將該結構應用于球拍設計和動力吸振器設計，研究表明，帶有阻尼的聲學黑洞結構能夠有效降低振動響應峰值；劉尊程等探究了二維聲學黑洞薄板的振動特性，并將其應用于浮筏結構上，研究表明內嵌二維聲學黑洞的浮筏結構可有效提升其隔振性能；李熙等[9-11]則從理論和試驗角度對聲學黑洞結構減振效果進行對比研究，研究表明，聲學黑洞結構減振效果良好，其結構參數對減振效果影響較大。

綜上可以看出，聲學黑洞具有結構簡單，抑振效果良好等特點，但在船舶浮筏系統中應用聲學黑洞過程中，由于浮筏結構形式限制，可嵌入聲學黑洞的區域較少，其對浮筏隔振性能的提升有限；為此，本文結合工程實際問題，提出分布式聲學黑洞應用方案，采用四個小尺寸聲學黑洞代替單個大尺寸聲學黑洞，利用數值仿真方法，依次探究了分布式聲學黑洞對平板結構、典型筏架結構以及浮筏隔振系統的抑振效果，最終以某船艙段為研究對象，采用分布式聲學黑洞方案，降低了船舶機械噪聲水平，能夠在有限區域內進一步提升聲學黑洞的抑振性能，為船舶減振降噪提供新的思路和參考。

1 聲學黑洞基本原理

聲學黑洞結構是基于天文學中黑洞概念提出的，聲學黑洞結構在厚度上滿足特定的冪律關系：h(x)=εxm(m≥2)，理想情況下，聲學黑洞結構具備彎曲波尖端無反射的特性，向結構尖端傳遞的彎曲波將被困在尖端，同時振動的能量也將在尖端匯聚并耗散。

一維聲學黑洞基本結構形式如圖1所示。

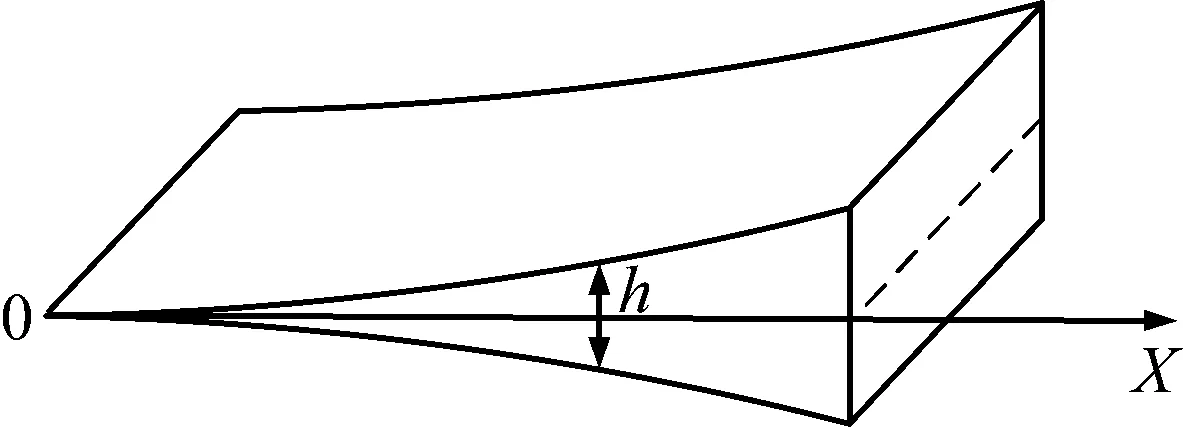
圖1 一維聲學黑洞結構示意圖Fig.1 Schematic diagram of one-dimensional ABH

根據文獻[1]中對聲學黑洞基本原理的描述可知：當彎曲波向聲學黑洞尖端邊界傳播時，結構上任一點到結構尖端整體波的相位為

(1)

式中，k(x)為彎曲波在結構上的局部波束。其具體指為

(2)

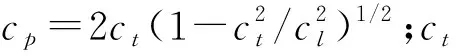
可以看出在特定頻率下，kp為一常數，在m大于等于2的條件下，當x趨于0則有k(x)趨于無窮，說明在結構尖端位置，局部波數趨于無窮，波長趨于0。即彎曲波永遠無法到達結構尖端位置，也將無法發生反射現象。實現聲學黑洞結構的減振效果。

將一維聲學黑洞截面，繞其尖端旋轉一周，形成中心凹陷的圓盤結構即為二維聲學黑洞，其基本結構形式如圖2所示。

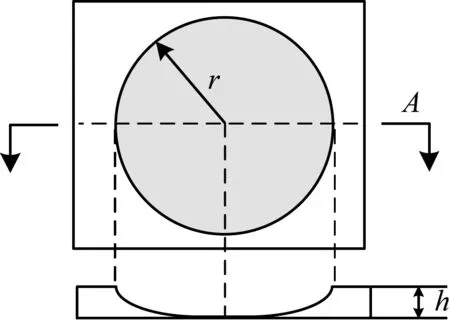
圖2 二維聲學黑洞結構示意圖Fig.2 Schematic diagram of two-dimensional ABH

彎曲波在二維聲學黑洞中傳播過程中，會在厚度變化區域發生偏轉，將匯集在聲學黑洞中心位置并耗散，實現對結構振動響應的抑制[12]。

但工程實際中，由于尖端厚度趨于0，使得結構加工較為困難，無法達到理論上對彎曲波的完全吸收，一般情況下，將對其尖端結構進行截斷，并附加一定的阻尼材料，以彌補尖端階段對聲學黑洞結構噪聲的負面影響。

2 分布式聲學黑洞浮筏系統設計

2.1 分布式聲學黑洞方案設計

本文采用四個聲學黑洞替代單個大尺寸聲學黑洞，形成分布式聲學黑洞應用方案，其中分布式聲學黑洞的半徑為單個聲學黑洞半徑的一半，保證兩種方案中聲學黑洞的面積相同。分布式聲學黑洞示意圖如圖3所示。

四個聲學黑洞的方案可以在保持聲學黑洞總面積恒定的條件下，不明顯改變聲學黑洞占用結構的區域。兩個或者三個聲學黑洞的方案則不具備上述的優勢。在分布式聲學黑洞方案中，聲學黑洞的位置以盡可能減小對原結構的改變為原則，均勻緊湊的分布在結構中。

為驗證分布式聲學黑洞方案的有效性，本章依次以平板結構、典型筏架結構為研究對象，開展分布式聲學黑洞對結構振動響應的抑制效果研究，并與單個聲學黑洞方案的抑振效果進行對比分析。

2.2 分布式聲學黑洞方案對結構抑振效果分析

2.2.1 分布式聲學黑洞平板結構振動特性分析

(1) 聲學黑洞平板模型

為驗證分布式聲學黑洞方案的有效性，對比單個聲學黑洞與分布式聲學黑洞方案對平板結構振動響應的抑制效果的差異，建立如圖4所示的聲學黑洞平板模型，主尺度為長360 mm，寬250 mm，厚6 mm，聲學黑洞區域黑洞結構半徑為100 mm，模型激勵點為水平中線距離右端50 mm位置處的P0點，激勵力載荷為單位力，振動響應考核點為P1～P8，其中，用點P1～P5的平均振動加速度級表示結構邊緣的振動水平，用點P6～P8的平均振動加速度級表示激勵點附近區域的振動水平，如圖4所示。

圖4(a)中聲學黑洞半徑為100 mm，厚度變化符合函數h(r)=6/10 000×r2，r為與聲學黑洞中心的距離，去除聲學黑洞結構中r<10 mm區域內的結構，并用恒定厚度板填充該區域，使得結構整體厚度變化連續，在聲學黑洞中心位置附加半徑為20 mm，厚度為2 mm的阻尼材料。圖4(b)為分布式聲學黑洞平板，嵌入四個小尺寸聲學黑洞，每個聲學黑洞半徑為25 mm，去除聲學黑洞結構中r<2.5 mm區域內的結構，阻尼材料半徑為5 mm。

在進行有限元建模分析時，采用具有不同厚度屬性的板單元來對聲學黑洞的變厚度區域進行建模，該方法解決聲學黑洞厚度連續變化帶來的網格劃分困難問題[13]，提高了計算效率，并且與實體單元模型的振動響應吻合良好。

(2) 聲學黑洞平板振動特性分析

采用有限元法對上述聲學黑洞平板進行相應分析，所建立的有限元計算模型如圖5所示，其中聲學黑洞區域被劃分為45個具有相同寬度的同心圓環，每個圓環具有不同的厚度屬性。

所得考核點平均振動響應曲線如圖6和7所示。

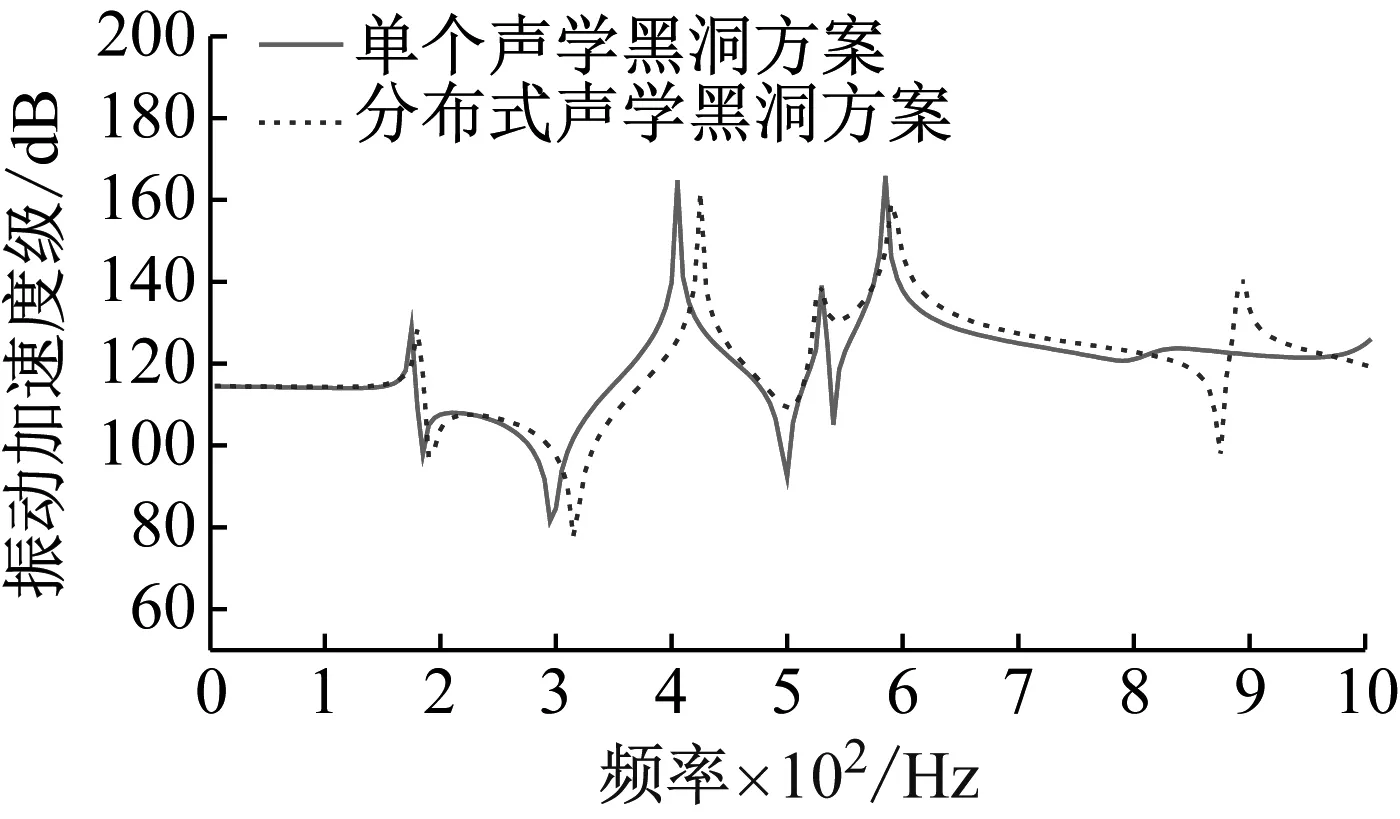
圖6 考核點P1～P5平均振動響應Fig.6 Average vibration response of points P1-P5

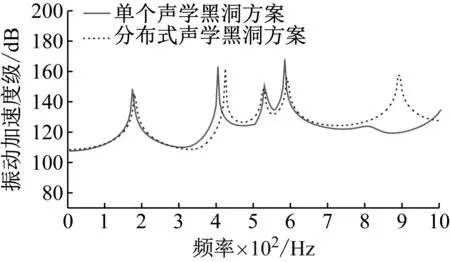
圖7 考核點P6～P8平均振動響應Fig.7 Average vibration response of points P6-P8

從圖6和7可以看出：分布式聲學黑洞平板的振動響應曲線在900 Hz產生了一個新的峰值，是由于分布式聲學黑洞嵌入后產生的新的振動模態所導致，但該處峰值大小較小；在前幾個峰值位置處，分布式聲學黑洞平板振動響應峰值均向高頻方向發生偏移，峰值大小約下降3～7 dB。說明四個聲學黑洞的設計將提高對低頻彎曲波的捕獲能力，降低聲學黑洞平板在低頻范圍內振動響應。

2.2.2 分布式聲學黑洞典型筏架結構振動特性分析

通過前文的研究可知，分布式聲學黑洞對平板的抑振效果更好，但筏架結構本身是相對復雜的三維立體結構，為此本節以典型筏架結構為研究對象，典型筏架結構具有筏架的基本特征結構，進一步探究分布式聲學黑洞方案對典型筏架結構的振動特性。

(1) 聲學黑洞典型筏架結構模型

筏架典型支撐結構如圖8所示的，其中上下面板長680 mm，寬580 mm，厚度為11 mm，垂向支撐板厚度為12 mm，上層隔振器連接板面板厚度為18 mm，下層面板隔振器連接板面板厚度為11 mm；筏架整體高度400 mm。

將幾何模型進行離散，保證每個波長中有6個網格，所得有限元模型如圖9所示。其中聲學黑洞嵌入位置為下層隔振器垂向支撐板中心，圖9(b)為單個聲學黑洞典型筏架，聲學黑洞半徑為96 mm，厚度變化符合函數h(r)=6/962×r2，r為與聲學黑洞中心的距離，去除聲學黑洞結構中r<9.6 mm區域內的結構，并用恒定厚度板填充該區域，使得結構整體厚度變化連續，在聲學黑洞中心位置附加半徑為19.2 mm，厚度為2 mm的阻尼材料，圖9(c)為分布式聲學黑洞典型筏架，聲學黑洞尺寸均為圖9(b)中聲學黑洞尺寸的一半。

(2) 聲學黑洞典型筏架結構振動特性分析

考慮到隔振器下表面通常采用四角螺栓連接方式，因此激勵點位置為上層隔振器面板共設有四個激振力，大小為單位力，考核點位置為下層隔振器面板的均方振速。經計算，得到1 000 Hz頻率范圍內不同計算模型的振動響應曲線如圖10所示。

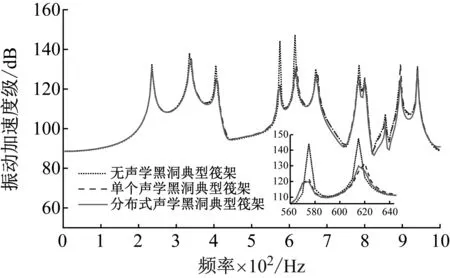
圖10 聲學黑洞典型筏架結構考核點振動響應曲線Fig.10 Vibration response curve of typical raft structure check point of ABH

從圖10中可以看出：

(1) 單個聲學黑洞或分布式聲學黑洞典型筏架結構能有效降低考核點在1 000 Hz以內的大部峰值的振動響應大小。

(2) 相比于無聲學黑洞典型筏架結構，分布式聲學黑洞典型筏架結構考核點的振動響應控制較好，大部分頻點減振效果可達3～9 dB，部分頻點減振效果更佳可達20 dB以上；

(3) 相比于單個聲學黑洞典型筏架，分布式聲學黑洞典型筏架響應曲線中大部分峰值減振效果提升1 dB以上，最多可提升3.8 dB。

綜上可以看出，分布式聲學黑洞方案能夠在不明顯改變結構的條件下，更好的對典型筏架結構的振動響應進行控制，提高了典型筏架結構的隔振性能。

2.3 分布式聲學黑洞浮筏系統模型

由前文可知分布式聲學黑洞方案可進一步提高典型筏架結構的隔振效果，本節將以某船舶大型浮筏隔振系統為基礎，設計分布式聲學黑洞浮筏系統。

在浮筏系統建模時，采用剛體對所承載的設備進行建模，其質量為2.1 t；采用4節點shell單元進行筏架結構和基座結構建模，筏架主尺度為模型總尺寸為3 500 mm×2 000 mm×400 mm；采用彈簧阻尼系統進行隔振器單元建模，上層隔振器12個，下層隔振器6個，隔振器參數如表1所示，最終浮筏隔振系統有限元分析模型如圖11所示。

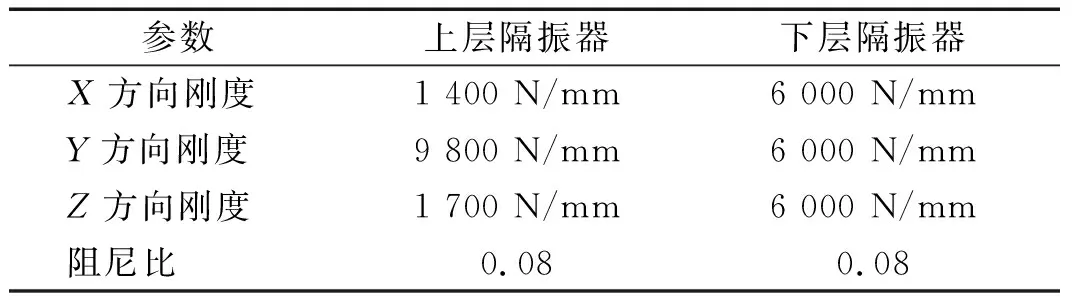
表1 隔振器參數Tab.1 Vibration isolator parameters

浮筏結構形式復雜，在確定聲學黑洞嵌入位置時，考慮到筏架結構受到激振力位置為上層隔振器的面板處，激振力產生的彎曲波將依次由面板傳遞至肘板、支撐板以及整個筏架結構，為了更好的對彎曲波進行吸收和耗散，本次聲學黑洞嵌入位置為筏架上層隔振器連接板肋板位置處，該位置距離激振點較近，是彎曲波傳播的主要路徑，此外，肘板結構應力分布呈現指端應力大，中心應力的小的規律，聲學黑洞的嵌入對原結構相對較小，結構依然連續完整，結構強度不是主要問題，本文暫不做討論。在分布式聲學黑洞方案中，為了使得聲學黑洞更均勻的嵌入在肘板結構中，采用三角形的排布形式，具體聲學黑洞嵌入方案及有限元模型如圖12所示。

3 分布式聲學黑洞浮筏系統性能分析

3.1 分布式聲學黑洞浮筏系統隔振性能分析

以振級落差作為評價筏架隔振性能的指標，振級落差計算公式如式(3)

LD=20lg(D)

(3)

式中：LD是振級落差，單位為dB；D為振動加速度的比值，D=a1/a2，其中a1表示設備機腳與隔振器相連位置的振動加速度，a2表示基座面板與隔振器相連位置處的振動加速度。計算所得筏架的振級落差曲線如圖13和14所示。

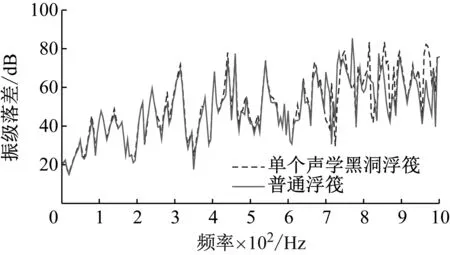
圖13 單個聲學黑洞浮筏隔振性能Fig.13 Vibration isolation performance of a single ABH floating raft

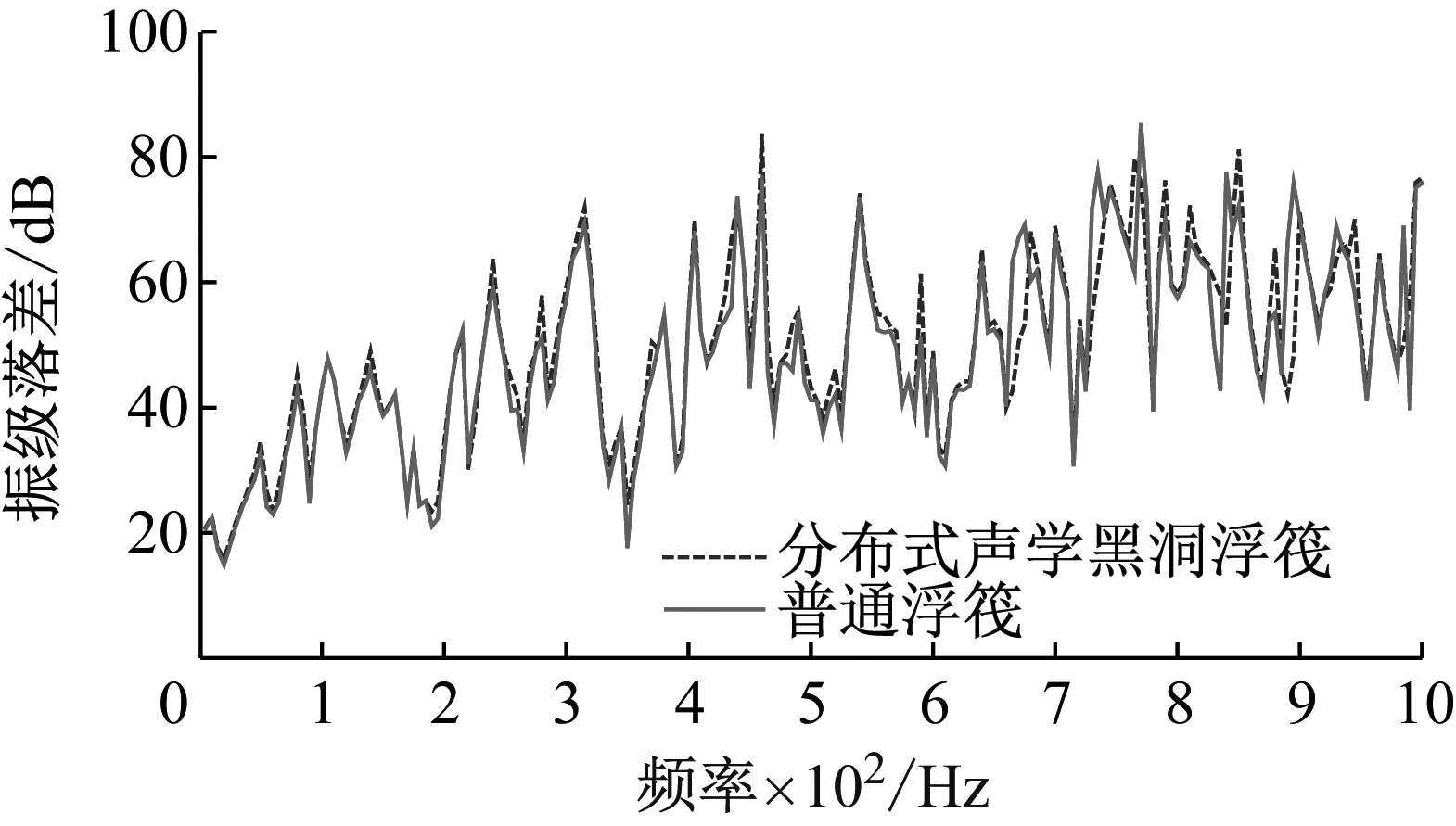
圖14 分布式聲學黑洞浮筏隔振性能Fig.14 Vibration isolation performance of distributed ABH floating raft

從圖13和14可以看出：

(1) 在5～1 000 Hz頻域范圍內，浮筏隔振系統的振級落差曲線的趨勢基本保持不變，但振級落差曲線中的多個峰值增大；說明在應用聲學黑洞后，對筏架振動特性的改變較小，但能夠對多個線譜進行控制。

(2) 在5～200 Hz的低頻范圍內，單個聲學黑洞浮筏隔振性能具有明顯提升的最低頻率為80 Hz，振級落差提升2.5 dB；分布式聲學黑洞浮筏隔振性能具有明顯提升的最低頻率為50 Hz，振級落差提升2.0 dB；說明分布式聲學黑洞的能夠拓寬聲學黑洞的工作頻率，降低聲學黑洞的最低工作頻率。

3.2 分布式聲學黑洞浮筏對船舶機械噪聲影響分析

3.2.1 艙段機械噪聲計算模型建立

基于某船總布置圖、基本結構圖、型線圖等圖紙資料，建立船舶艙段的有限元模型，如圖15所示，采用板單元建立艙段殼體，縱骨等小型扶強材采用梁單元建立，并保證一個波長內至少含有6個網格，采用聲固耦合法開展艙段機械噪聲計算。

3.2.2 激勵載荷

激勵載荷大小為某設備機腳振動加速度的實測激勵載荷，所得10～200 Hz下的頻域激勵載荷如圖16所示。

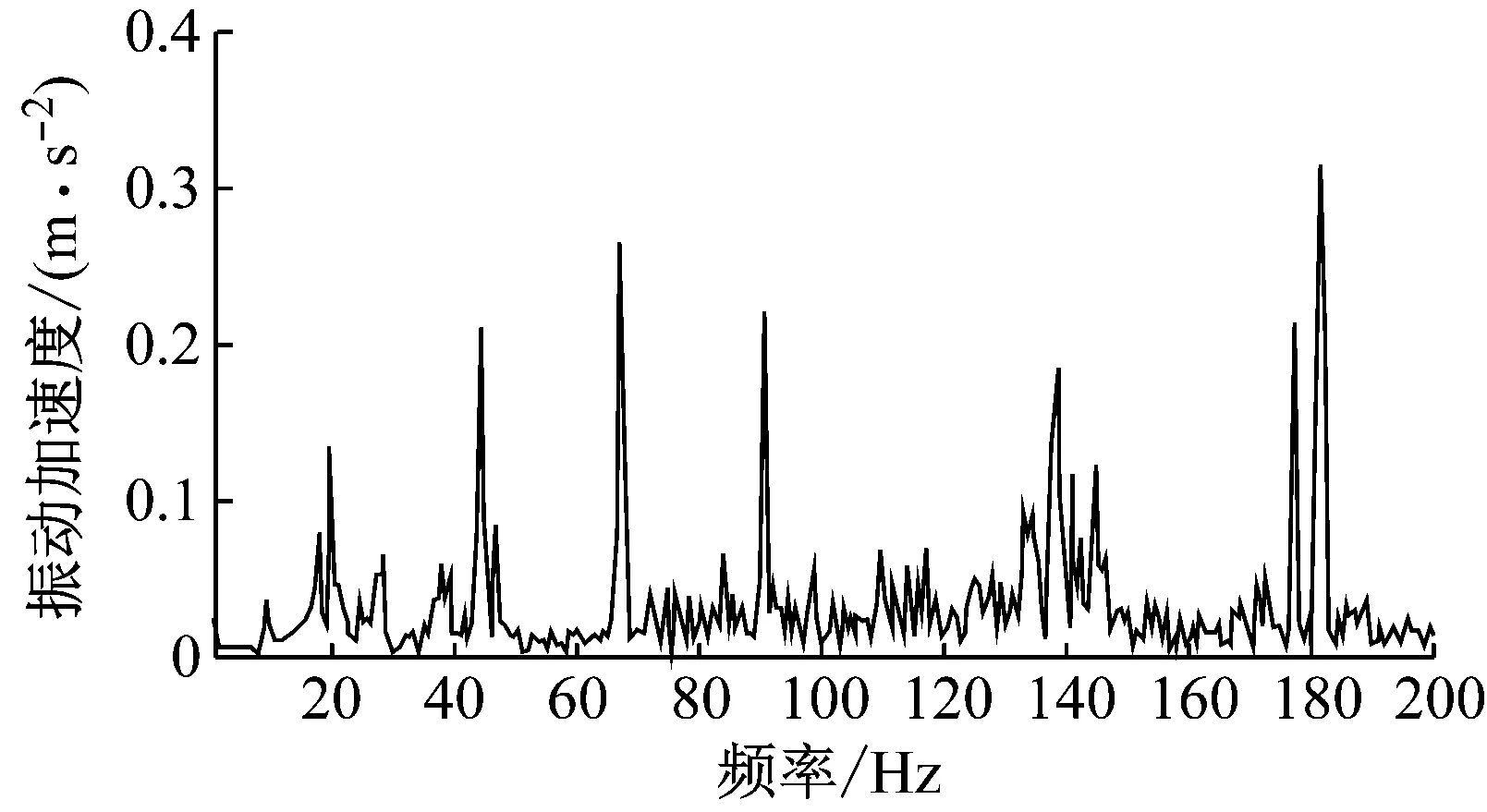
圖16 某設備實測激勵載荷Fig.16 Measured excitation load of a certain equipment

3.2.3 艙段機械噪聲計算結果及分析

本次計算的考核指標為艙段機械噪聲聲源級，通過有限元計算，得到艙段機械噪聲聲源級線譜如圖17所示。

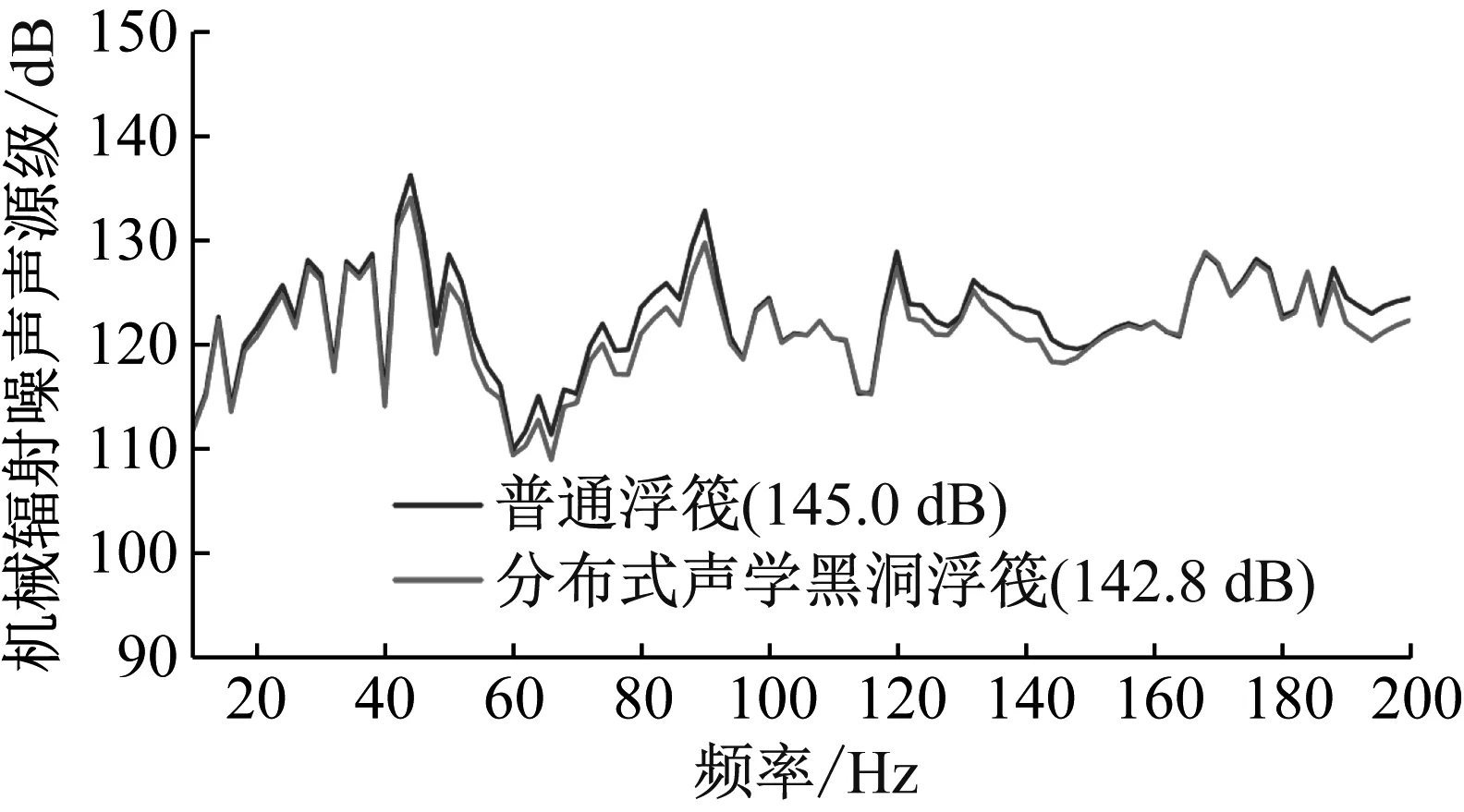
圖17 分布式聲學黑浮筏應用前后機械噪聲Fig.17 Mechanical noise before and after the application of distributed ABH raft

在某設備實測激勵力載荷的作用下，艙段機械噪聲出現三個較為明顯的峰值，分別為44 Hz、90 Hz、120 Hz，上述頻點的機械噪聲聲場分布如圖18所示。

從機械噪聲曲線中可以看出：

(1) 在普通筏架中，10～200 Hz頻域范圍內的機械噪聲總級為145.0 dB，而分步式聲學黑洞筏架的機械噪聲總級為142.8 dB，下降2.2 dB，降噪效果良好。

(2) 在應用分布式聲學黑洞浮筏后，機械噪聲在45～90 Hz，120～150 Hz等多個低頻范圍內下降2 dB以上，可見分布式聲學黑洞浮筏系統能夠有效控制船舶低頻機械噪聲。

4 結 論

本文提出分布式聲學黑洞應用方案，以平板結構、典型筏架結構驗證了分布式聲學黑洞能夠進一步提升對結構振動響應的抑制效果，并開展了分布式聲學黑洞浮筏隔振系統隔振性能研究，最后計算了分布式聲學黑洞浮筏隔振系統對船舶機械噪聲的影響，具體結論如下:

(1) 分布式聲學黑洞相比單個聲學黑洞具有更好的抑振效果，能夠在有限區域內進一步提升聲學黑洞的抑振性能。

(2) 相比于單個聲學黑洞，分布式聲學黑洞可降低平板結構振動響應的峰值約3～7 dB；可降低典型筏架結構振動多個響應峰值1 dB以上。

(3) 分布式聲學黑洞使得浮筏隔振性能在低頻范圍內提升，相比單個聲學黑洞，分布式聲學黑洞最低工作頻率可達50 Hz，振級落差提升效果為2 dB。

(4) 分布式聲學黑洞浮筏的使得船舶機械噪聲在在45～90 Hz，120～150 Hz等多個低頻范圍內下降2 dB以上，機械噪聲在10～200 Hz低頻范圍內總級下降2.2 dB，降噪效果良好。