帶浮力塊立管的橫流-順流雙向渦激振動響應研究

莊陳怡， 李宇坤， 袁昱超， 薛鴻祥， 唐文勇

(1.上海交通大學 海洋工程國家重點實驗室，上海 200240;2.上海交通大學 船舶海洋與建筑工程學院，上海 200240)

隨著海洋油氣開發向深水領域進軍，立管需要足夠大的頂部張力以維持自身穩定性，然而由于頂部張力器附近立管材料強度和接頭強度的限制，必須設置浮力塊對立管提供分布式浮力，以減小系統濕重、降低對立管張力器張力的要求。浮力塊的增設使頂張式立管的張力及重量分布發生變化，導致固有頻率、振型、曲率等模態特性發生改變。此外浮力塊將增大立管的水動力外徑，這將造成兩方面的影響：對于能量輸入區，較高的水動力外徑會增加流體向立管結構的能量輸入，增大激勵力；對于能量輸出區，會增加流體阻尼。因此，帶浮力塊立管的動力響應特性與裸管相比存在明顯差異。

目前，國內外對于立管渦激振動(vortex-induced vibration, VIV)機理已有較為深入的研究[1-3]，但對于布置有浮力塊裝置的立管渦激振動特性的研究較有限，主要研究方法分為模型試驗和數值模擬。Lie等[4]在挪威MARINTEK拖曳水池中，對均勻流和線性剪切流下4種不同浮力塊覆蓋率的立管振動進行試驗，分析了立管橫流向的試驗數據，評估交錯布置的浮力塊對船用立管渦激振動的影響。SHELL Exploration and Production在MARINTEK測試了均勻流下5種不同浮力塊交錯布置方案立管模型的VIV響應情況，Rao等[5]針對“何種浮力塊覆蓋率下，浮力塊引起的激勵頻率主導立管的VIV響應”這一問題，分析了橫流振動試驗數據。挪威深水計劃在MARINTEK 對6種不同浮力塊交錯布置立管進行水動力模型試驗，Wu等[6]對橫流向試驗數據進行分析，總結了相鄰浮力塊段與裸管段長度比、浮力塊長徑比、浮力塊覆蓋率對于立管渦激振動的影響。數值模擬方面，Wu等[7-8]以SHELL Exploration and Production在MARINTEK開展的交錯浮力塊立管試驗為數據基準，采用VIVANA軟件預報了浮力塊立管橫流向的渦激振動響應，基于試驗調整了激勵力系數庫，并與試驗結果進行對比，針對另一較小尺度立管進行了類似工作。孫友義等[9]使用SHEAR7程序對帶有浮力塊的隔水管進行渦激振動分析，研究不同浮力塊分布形式對隔水管系統渦激振動疲勞特性的影響，對浮力塊分布方案進行優化。工程上及相關研究表明[10-12]，合理的浮力塊布置可減小立管的疲勞損傷，從而延長立管的疲勞壽命，提高立管結構安全性。

對帶有浮力塊裝置柔性立管渦激振動的研究具有工程價值，而針對此種立管渦激振動研究的有限性使其響應特性及機理尚未清晰可知，且現存的渦激振動預報模型大多以橫流向渦激振動為主要研究目標[13]，忽略了橫流向與順流向振動間明顯存在的耦合效應[14]。為了與實際工程更為緊密的結合，有必要針對布置有浮力塊的立管渦激振動建立有效的雙向響應預報模型以深入研究其渦激振動特性。本文針對帶有浮力塊的頂張式立管，基于雙自由度受迫振動試驗數據，采用有限元法和能量平衡方程建立了考慮雙向耦合效應的渦激振動頻域預報模型，分析不同布置方式浮力塊立管的渦激振動響應，研究浮力塊布置的優化方案。

1 立管雙向渦激振動頻域預報模型

1.1 立管振動方程

將頂張式立管簡化為受軸向張力作用的簡支梁，坐標原點位于立管懸掛點，z軸向下為正，x軸為順流方向，y軸為橫流方向。將簡支梁在空間上進行有限元離散，得到單元剛度矩陣K=KM+KT，其中：

(1)

(2)

梁單元集中質量矩陣可寫為

(3)

式中：KM與KT分別為立管單元抗彎剛度矩陣和軸向張力提供的附加剛度矩陣；EI為彎曲剛度，由于浮力塊裝置的剛度極小，本文忽略浮力塊對立管彎曲剛度的影響，認為彎曲剛度沿立管均勻分布；T為軸向張力，浮力塊的布置將改變立管各位置處的張力分布；l為單元長度；m0為立管結構單位長度質量，浮力塊將改變立管結構的質量分布；ma=CaρπD2/2為單位長度附加質量；Ca為附加質量系數；ρ為流體密度；D為立管直徑，對于帶有浮力塊的立管段即為浮力塊直徑。

引入簡支梁頂端和底端的約束條件，按照單元節點坐標組裝得到總剛度矩陣[KM+KT]和質量矩陣[M]后，可得振動方程

[KM+KT]φ-ω2[M]φ=0

(4)

式中：ω為圓頻率，f=2π/ω即為固有頻率；φ為模態振型。通過求解矩陣方程即可得到簡支梁不同模態的頻率和振型。

圖1 橫流方向附加質量系數簡化曲線Fig.1 Simplified curve of added mass coefficient in CF direction

圖2 順流方向附加質量系數簡化曲線Fig.2 Simplified curve of added mass coefficient in IL direction

至此，可進行立管固有頻率及振型的計算。考慮浮力塊的影響，計算中D為立管各處實際水動力直徑。橫流方向上，立管響應頻率及振型通過迭代計算得到：

(1) 假設Ca,CF=1，求解振動方程得到立管固有頻率fCF,0；

(3) 根據橫流方向附加質量系數簡化曲線得到附加質量分布，更新振動方程，計算得到新的振動頻率fCF,k+1；

(4) 重復步驟(2)、(3)直至結果收斂，得到橫流向實際振動頻率fCF和振型φCF(z)。

由于基于順流方向附加質量系數計算得到的振動頻率并不總是滿足為橫流響應頻率的兩倍，常出現2fi,CF落于fj,IL、fj+1,IL兩者之間的情況，因此需要對順流附加質量進行調整。在本文模型中通過減小順流向附加質量的方式增大固有頻率，以滿足fj,IL=2fi,CF。順流方向上立管響應頻率及振型計算過程如下：

(2) 根據附加質量系數分布曲線得到順流向附加質量分布，建立振動方程，計算第i階橫流向振動模態對應的順流向模態及頻率；

(3) 對比fj,IL和fi,CF，調整順流向附加質量，直至滿足fj,IL=2fi,CF，并得到實際順流向振型φj,IL(z)。

1.2 渦激振動流體力模型

1.2.1 激勵力模型

采用Zheng試驗得到的橫流向和順流向渦激振動激勵力系數計算流體對立管的激勵力。與單自由度強迫振動試驗不同，Zheng所進行的試驗反映出了橫流與順流振動間存在的耦合效應，并在激勵力系數上體現。以0°位移相位角為例，典型激勵力系數分布云圖如圖3和圖4所示。可以發現，隨順流振幅增大，橫流向激勵中心所對應無因次頻率減小；而順流向激勵力系數將隨橫流振幅呈現增大趨勢。參考文獻[14]，將立管橫流向無因次頻率介于0.125～0.25之間的區域作為能量輸入區。根據無因次響應頻率及幅值進行插值可獲得相應的橫流及順流向激勵力系數，本文通過改變水動力直徑考慮浮力塊引起的激勵力系數及激勵力變化。

1.2.2 阻尼模型

當立管結構響應超出能量輸入區范圍時，認為流體作用力將轉變為水動力阻尼。本文使用Venugopal[16]針對渦激振動提出的經驗阻尼模型，該模型分為高流速區和低流速區。

高流速區水動力阻尼系數為

rhh=ρU2(z)Cvh/ω

(5)

低流速區水動力阻尼系數為

rhl=rsw(z)+ρDU(z)Cvl

(6)

1.3 渦激振動響應幅值計算

參考SHEAR7方法，通過預估能量選取振動激發模態[17]。針對橫流向振動模態i及對應順流向振動模態j，計算預估能量

(7)

其中，

(8)

(9)

選取激發振動模態時，根據最大預估能量值Πmax，計算各橫流-順流振動模態組合預估能量比Πi&j/Πmax，以0.7為能量閾值，選取橫流及順流向渦激振動激發模態。

其中，模態激勵力為

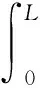
(10)

式中：Y(z)=Ay|φCF(z)|/D為立管各位置橫流向振幅；X(z)=Ax|φIL(z)|/D為立管各位置順流向振幅。針對裸管段和浮力塊段，通過改變直徑計算各段的激勵力和預估能量。

立管模態速度為

Vi(t)=Aiωisin(ωit)

(11)

模態阻尼為

(12)

針對渦激振動激發的橫流向模態i及順流向模態j建立能量平衡方程，可得模態振幅

(13)

(14)

同時，本文通過模態疊加法處理柔性立管多階模態同時被激發的現象。綜上，頂張式立管渦激振動響應計算流程如圖5所示。此前已有工作驗證了此預報模型用于預報裸露立管渦激振動響應的準確性[18]。

圖5 渦激振動預報流程圖Fig.5 The flow chart of VIV prediction

1.4 疲勞損傷計算

立管渦激振動使結構受交變彎矩作用。根據平斷面假設，第i階振動模態引起彎矩為

(15)

對應產生的最大彎曲應力為

(16)

根據Miner線性累計假設及S-N曲線，可以得到第i階模態下渦激振動引起的疲勞損傷分布

(17)

式中：fi為渦激振動響應頻率；TD為立管使用時間；A和m為S-N曲線參數；SCF為應力集中系數。

由于頂張式立管發生渦激振動響應時往往存在多種模態成分，疲勞損傷由各模態共同產生。本文使用SRSS(square root of the squre stress)方法計算渦激振動疲勞損傷

(18)

2 不同浮力塊覆蓋率下立管渦激振動響應

目前工程上認為浮力塊交錯分布有助于降低渦激振動對立管造成的疲勞損傷[19-20]。本節選取一實尺度立管作為算例，研究25%、50%、100%浮力塊覆蓋率下立管渦激振動響應，并與裸管進行比較。浮力塊的形狀為有一定厚度的環形塊體，包裹于立管外圍，浮力塊模型及四種覆蓋率下浮力塊分布如圖6所示，其中浮力塊間隔均布設置：25%覆蓋率情況下每隔30 m布置10 m長浮力塊，50%覆蓋率情況下每隔20 m布置20 m長浮力塊。

圖6 浮力塊模型及不同浮力塊覆蓋率下立管模型Fig.6 Buoyancy module model and riser models with different buoyancy module coverage

該算例立管工作水深1 000 m，立管外徑為0.508 m，壁厚為0.025 4 m，單位長度質量為536.46 kg/m，彈性模量為2.1×1011N/m2，浮力塊外徑為1.193 8 m，單位長度質量為258.73 kg/m，提供凈浮力為312.27 kg/m，立管底端張力取0.5倍裸管濕重。海流為線性剪切流，海底速度為0，海面流速為0.4～2.0 m/s。疲勞損傷計算選取DNV給出的有陰極保護的海洋結構物S-N曲線[21]。

靜水中立管前20階固有頻率見圖7。在設置浮力塊后由于立管整體質量增大、張力減小，立管的固有頻率降低。其中在立管全部覆蓋浮力塊的情況下，頻率約為裸管的50%。

圖7 不同浮力塊覆蓋率下立管固有頻率Fig.7 Natural frequencies of riser with different buoyancy module coverage rates

圖8為四種浮力塊覆蓋率立管模型在不同流速剪切流作用下的渦激振動響應頻率。可以發現，四種覆蓋率下立管模型渦激振動響應頻率明顯落于兩條趨勢線附近，分別對應于立管和浮力塊外徑的斯托哈爾頻率。由于浮力塊的外徑遠大于立管直徑，當渦激振動由浮力塊所控制時響應頻率明顯低于立管控制情況。對于50%覆蓋率立管模型，立管響應完全由浮力塊所控制，響應頻率落于斜率較小的趨勢線附近。而對于25%覆蓋率的立管模型，響應頻率離散分布在兩條趨勢線附近，表明在該覆蓋率下渦激振動響應將由兩種水動力外徑共同控制，即流體通過浮力塊向結構輸入的能量與通過立管向結構輸入的能量相當。

圖9為四種浮力塊覆蓋率立管模型在不同流速下的渦激振動最大疲勞損傷。全部覆蓋浮力塊時立管最大疲勞損傷略高于裸管情況，并且在順流方向上較為明顯。而25%及50%覆蓋率情況下立管最大疲勞損傷較低。25%覆蓋率立管模型的響應頻率由裸管與浮力塊共同控制，從而使模型不易發生渦激振動，具有較好的疲勞特性；值得注意的是，25%浮力塊覆蓋率下，損傷在1.4～1.6 m/s的流速范圍內產生了隨流速增大而減小的變化，這與激發模態有關，從圖8可以看到，1.4 m/s流速下立管只有一個低激發頻率，而1.6 m/s流速下存在兩個低激發頻率，后者更趨向于造成較小的疲勞損傷。50%覆蓋率模型的響應頻率由浮力塊控制，因浮力塊交錯分布擾亂了沿立管軸向漩渦泄放的一致性，從而降低了漩渦對系統的能量輸入，因此50%覆蓋模型的疲勞特性要明顯優于100%覆蓋模型。可見對于頂張式立管，布置一定覆蓋率的浮力塊在減少頂部張力需求的同時可有效降低由渦激振動引起的立管疲勞損傷。

以海面流速為1.2 m/s工況為例對立管渦激振動響應進行具體分析，響應位移沿立管分布如圖10所示。其中，25%覆蓋率情況下渦激振動響應由立管及浮力塊共同控制，使得“頻率鎖定”現象不易發生，響應位移僅為裸管的1/3。50%覆蓋率情況下渦激振動響應由浮力塊控制，浮力塊間隔布置削弱了瀉渦強度并使結構中輸入能量減少，且響應模態階次降低，其響應位移與裸管情況下較為接近。而在全部覆蓋浮力塊后，固有頻率的降低使響應模態與裸管相比沒有發生明顯變化，而水動力直徑的增大令立管響應位移大幅增加。

立管疲勞損傷沿管長分布如圖11所示。100%覆蓋率情況下立管的疲勞損傷最高，全浮力塊分布方案造成立管水動力外徑增大，外部流體對模型的輸入能量大幅提高,導致疲勞損傷增加，尤其是在高流速區可達到裸管疲勞損傷的1 000倍。50%覆蓋率下立管由于振動頻率及模態階次較低，疲勞損傷相對較小。而對于25%情況，雖然其響應位移為四種浮力塊覆蓋率情況下最小的，但是渦激振動響應中存在的高階模態成分導致疲勞損傷與50%覆蓋率下立管處在同一水平上。同一流速工況下，不同浮力塊布置方案的立管模型其響應位移與疲勞損傷呈現非一致性，因此以抑制疲勞損傷為目標進行浮力塊布置方案優化時，還需兼顧考慮立管位移響應幅值。

3 浮力塊布置方案優化

為研究不同浮力塊布置方式對頂張式立管渦激振動的影響，針對25%浮力塊覆蓋率的立管模型，對比圖12所示四種布置方案下渦激振動響應特性。其中，方案1浮力塊均勻間隔布置，方案2布置在高流速區，方案3布置在立管中段，方案4布置在低流速區。

圖12 不同浮力塊布置方案的立管模型Fig.12 Riser models with different buoyancy module arrangements

圖13～15分別為四種浮力塊布置方案立管在不同流速下的渦激振動響應頻率、響應位移及最大疲勞損傷。在不同流速工況下同一浮力塊布置方案將在響應頻率上呈現相同的特性：其中方案1的渦激振動響應由立管和浮力塊共同控制；方案2的響應由浮力塊控制；方案3和方案4則由立管控制。分析表明：立管響應頻率由處于高流速區的模型水動力直徑決定；處于低流速區的浮力塊對響應頻率起不到控制作用，僅可對響應位移產生影響。

方案1的響應頻率由浮力塊與立管共同控制，不易發生渦激共振，且浮力塊的交錯分布降低了旋渦強度，疲勞損傷特性整體較優，同時響應位移最小。方案2立管的渦激振動響應由浮力塊控制，響應模態階次及響應頻率相對較低，疲勞損傷與方案1較為接近，具有較好的疲勞特性，但是在該方案中由于浮力塊置于高流速區中，流體將通過浮力塊向結構中輸入大量的能量，令立管產生遠大于其他三種方案的位移響應。方案3和方案4的渦激振動響應由立管控制，響應模態階次高、頻率大，導致疲勞損傷程度整體較高；尤其在方案4中，立管損傷遠超其他布置方案，同時由于處于激勵狀態的裸管段處于中高流速區，結構的能量輸入較大，而浮力塊位于低流速區，其產生的流體阻尼效應較小，導致立管整體出現較大的響應位移。因此，從整體看，方案1為較優的浮力塊布置方案。

4 結 論

基于本文研究，得出如下結論：

(1) 布置浮力塊將明顯改變立管渦激振動特性。立管全部覆蓋浮力塊將加劇響應位移與疲勞損傷；而在25%及50%覆蓋率下間隔布置浮力塊會影響流體瀉渦沿管長分布的一致性，使得流體向結構輸入的能量較少，導致立管渦激振動響應幅值相對較小，并有效降低渦激振動引起的疲勞損傷。

(2) 從降低渦激振動疲勞損傷的角度出發，對頂張式立管設置浮力塊時，應盡量使其動力響應由浮力塊和裸管段共同控制，以抑制渦激振動。同時還可在減小高流速區內浮力塊分布長度的前提下，令渦激振動響應由浮力塊單獨控制，這樣既能減小響應位移，又可降低立管的振動模態階次及響應頻率，改善結構疲勞性能。

(3) 對于本文研究的25%浮力塊覆蓋率情況，推薦將浮力塊間隔布置，此時立管具有較好的疲勞特性且響應位移最小。