不同失穩形態黃土邊坡的動力響應研究
孫 文,梁慶國,,喬向進,曹小平,王麗麗
(1.蘭州交通大學 土木工程學院,甘肅 蘭州 730070;2.蘭州交通大學 土木工程國家級實驗教學示范中心,甘肅 蘭州 730070;3.甘肅省道路橋梁與地下工程重點實驗室,甘肅 蘭州 730070;4.中國地震局蘭州地震研究所黃土地震工程重點實驗室,甘肅 蘭州 730000)
我國黃土地區分布廣泛,隨著國家西部政策的推進,黃土地區工程數量不斷增多,結合西部地區抗震設防烈度普遍較高的特點,亟需針對黃土邊坡地震失穩過程和機制開展進一步研究,完善相應的抗震設計依據[1-4]。一般來說,在地震過程中陡坡和緩坡的破壞過程差異明顯,二者的地震動力響應和失穩機制也不盡相同[5-6]。以言志信等[7]、葉海林等[8]為代表,在邊坡動力響應研究方面取得了豐碩的研究成果。在前人的基礎上,近年來邊坡動力穩定性的研究更加系統[9-10]。劉新榮等[11]針對三峽水庫蓄水后微小地震頻發的現象,通過振動臺試驗和離散元的結合,研究了頻發微震作用下巖質邊坡的損傷演化機理。夏坤等[12]通過數值模擬及大型振動臺試驗的方法,研究了地震作用下,西北地區黃土塬邊坡加速度響應與坡高的關系。王蘭民等[13]研究了黃土邊坡在降雨和地震耦合作用下的動力響應,對該工況黃土邊坡的失穩過程進行了分類。
目前,關于邊坡地震動力響應研究,多集中在對PGA和Fourier變換的結果進行時域和頻域分析上。相關的研究成果已非常豐富,研究方法也較為成熟。但是,Fourier變換這種頻域分析方法較為單一、定性,無法反映信號的非平穩、持時短、時域和頻域局部化等特性,需要一種更加精細的分析方法。小波包變換具有同時反映信號時域和頻域特征的優點,因此本文引入小波包變換的分析方法[14],分解加速度響應信號,得到不同頻段的能量占比,以不同頻段的能量占比變化為切入點,結合邊坡的失穩破壞過程進行分析,以期為相關研究和工程提供借鑒。
1 模型試驗設計
1.1 地震波加載方案
為排除在某單一地震波振動下,模型的失穩和動力響應為偶然特征現象,不能代表普遍規律的可能性,同時最大限度地利用模型,試驗采用汶川湯峪波和El-Centro波兩種波形,由弱到強交替加載的方式,加載工況共設計18個。第一臺邊坡模型坡度較陡,預計失穩所需振幅較小,設計加載前12個工況;第二臺邊坡模型坡度相對較緩,設計加載全部18個工況。加載工況見表1。
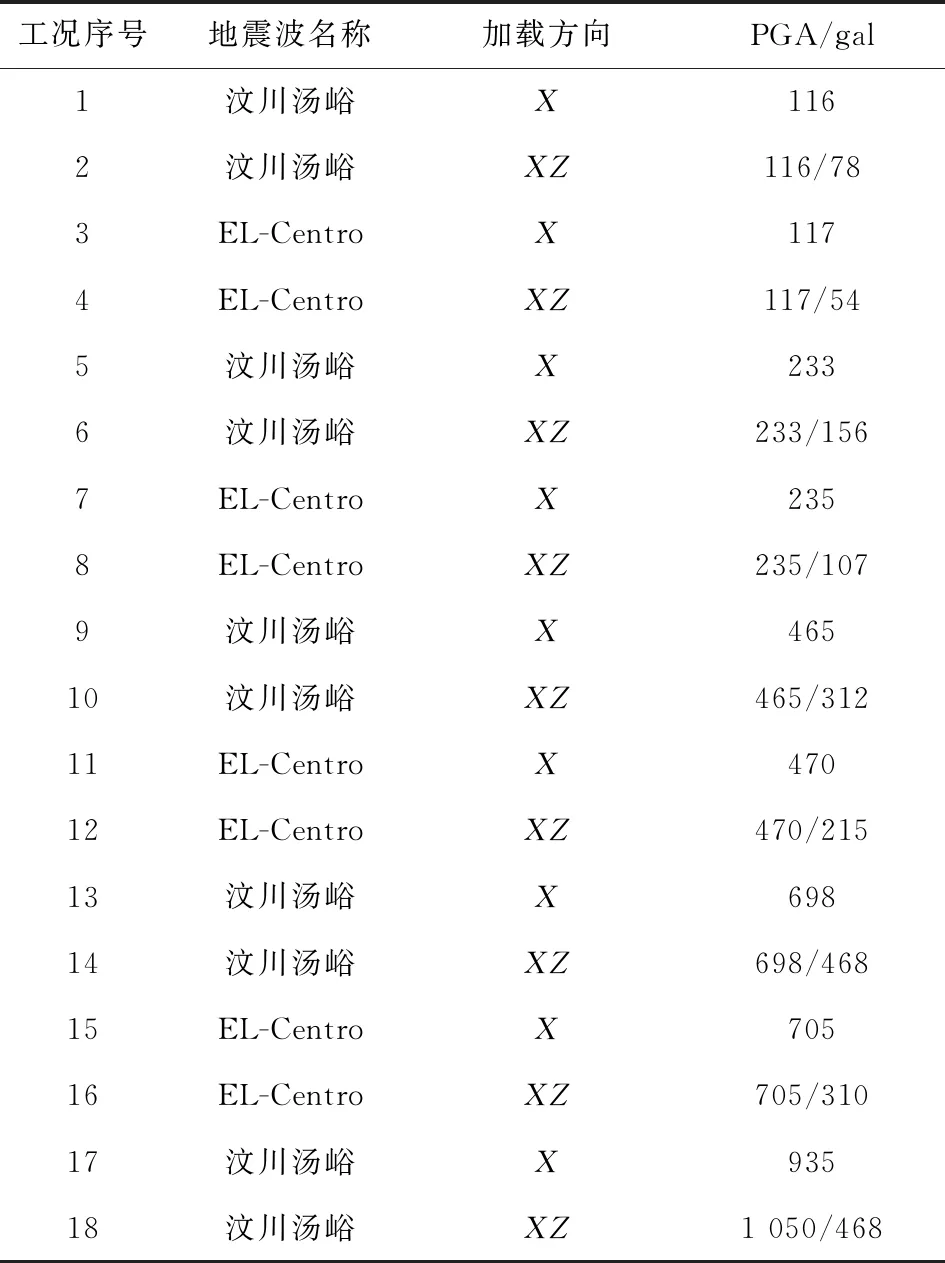
表1 地震波加載工況
1.2 模型設計
模型試驗原型為天然黃土邊坡,幾何相似比為1∶20。通過正交設計,進行模型土的配比試驗,最終確定以原狀黃土∶重晶石粉∶鋸末∶水=0.835∶0.04∶0.015∶0.11的配比進行模型重塑黃土的配制[15]。相似參數見表2。

表2 相似參數
試驗在大型電伺服式振動臺上進行。該震動臺有效加載頻率為0.1~50.0 Hz。第一臺邊坡模型坡度60°,坡高48 cm,第二臺邊坡模型坡度45°,坡高110 cm,邊坡模型均采用分層壓實的填筑方法。在填筑的過程中,在沿邊坡中軸線斷面相應位置埋入加速度傳感器,編號分別為A1~A15和A1~A25。為了減弱“模型箱效應”的邊界影響,增加底部的摩阻力,在模型箱側面和底部分別鋪設了聚乙烯閉孔泡沫板和水泥砂漿黏結的鵝卵石。兩臺試驗模型及加速度傳感器埋設位置見圖1。
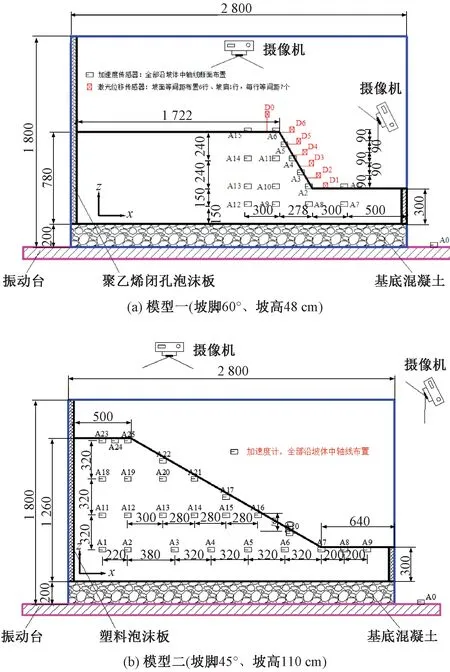
圖1 邊坡模型試驗設計簡圖(單位:mm)
2 加速度響應信號的小波包變換
2.1 小波包層數及頻段劃分
小波包對地震波的低頻部分和高頻部分均可進行分解,此外,小波包分析能根據分析要求和信號特性選擇相應信號頻譜與頻帶進行匹配,是一種能對信號進行時頻精細化分析的方法[14]。雖然在理論上,小波包分解的層數是沒有上限的,但是,分解層數過低或過高都不利于對地震波信號的分析。小波包分解層數為[16-17]
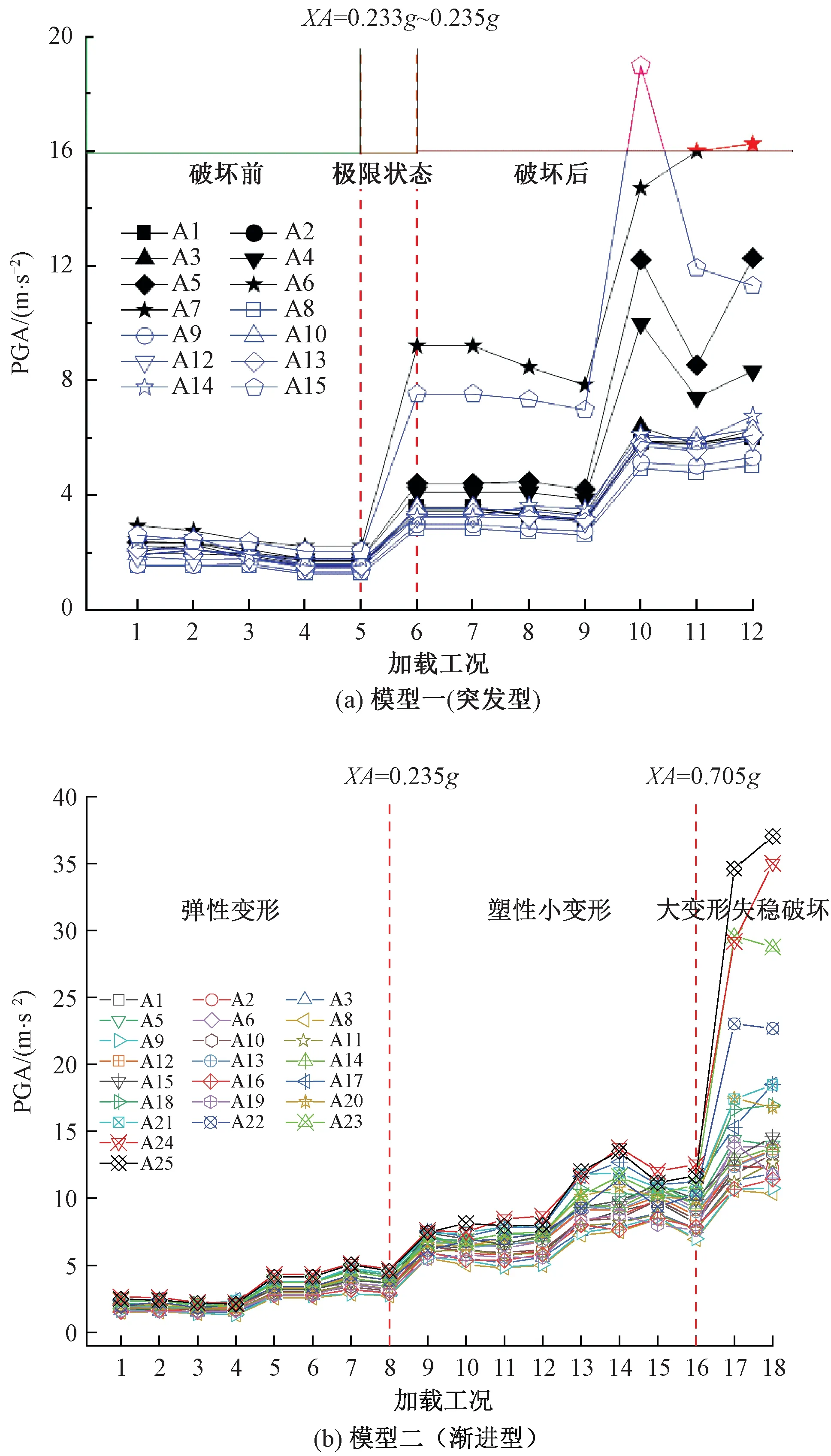
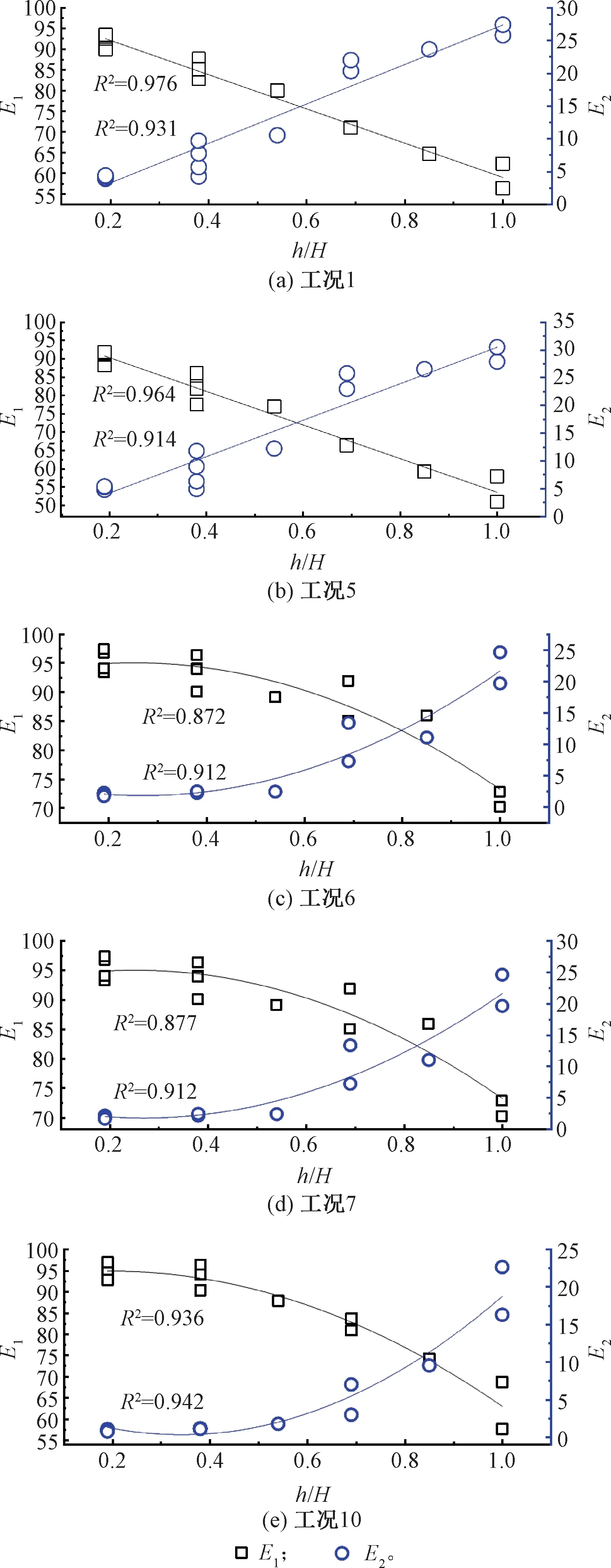
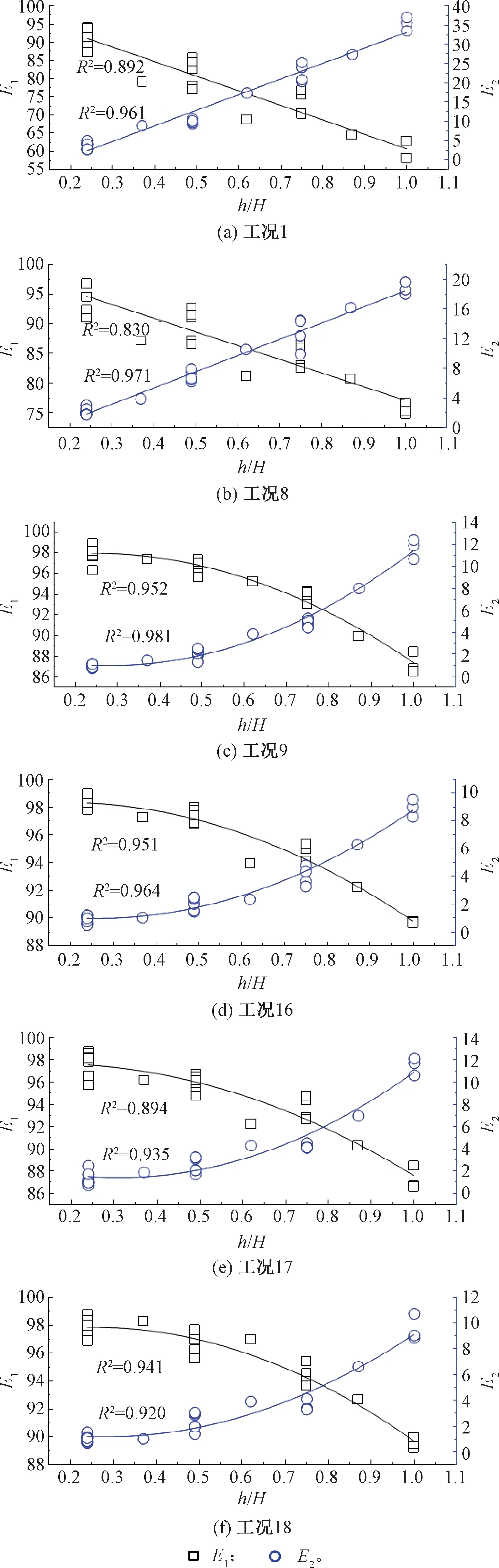
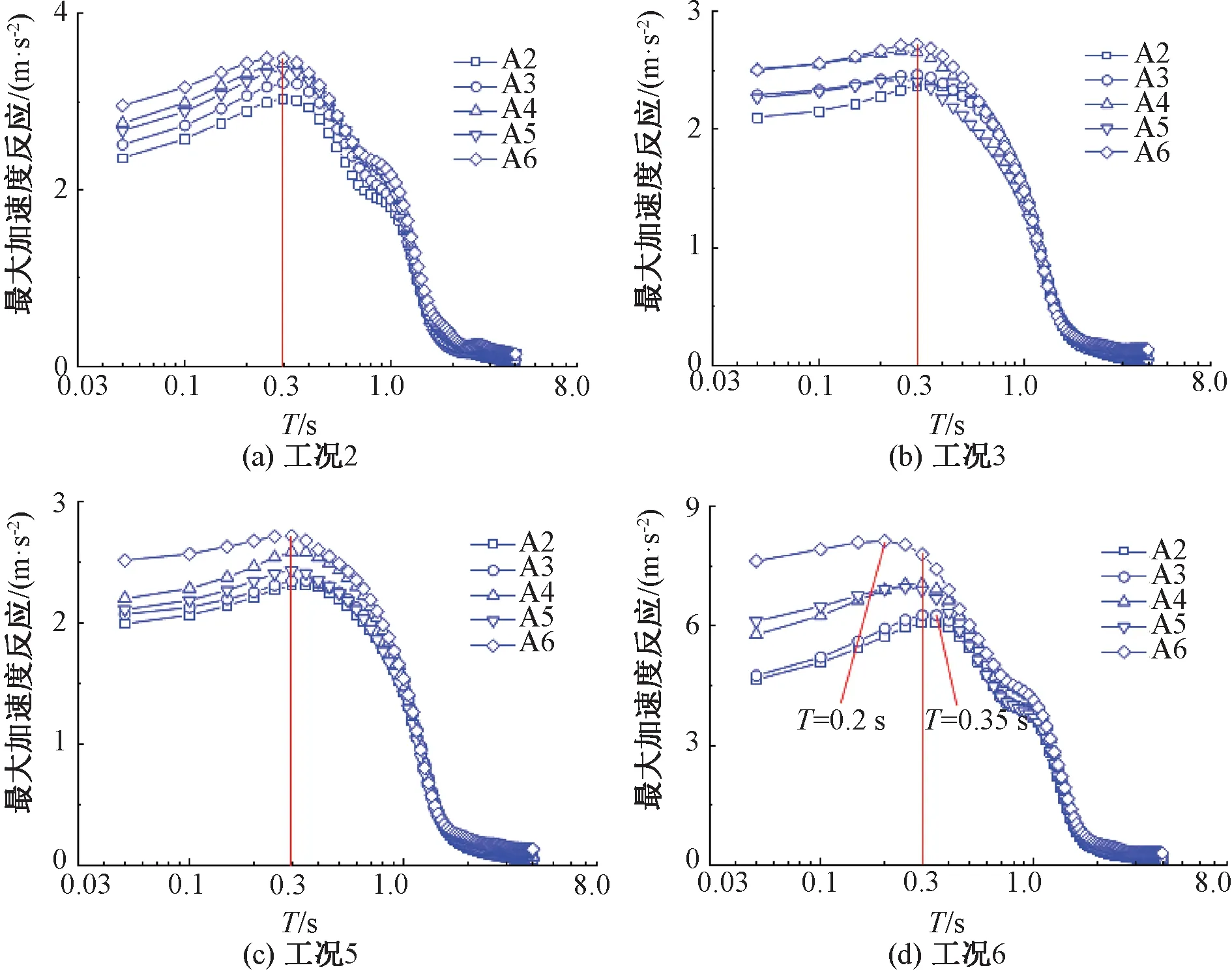
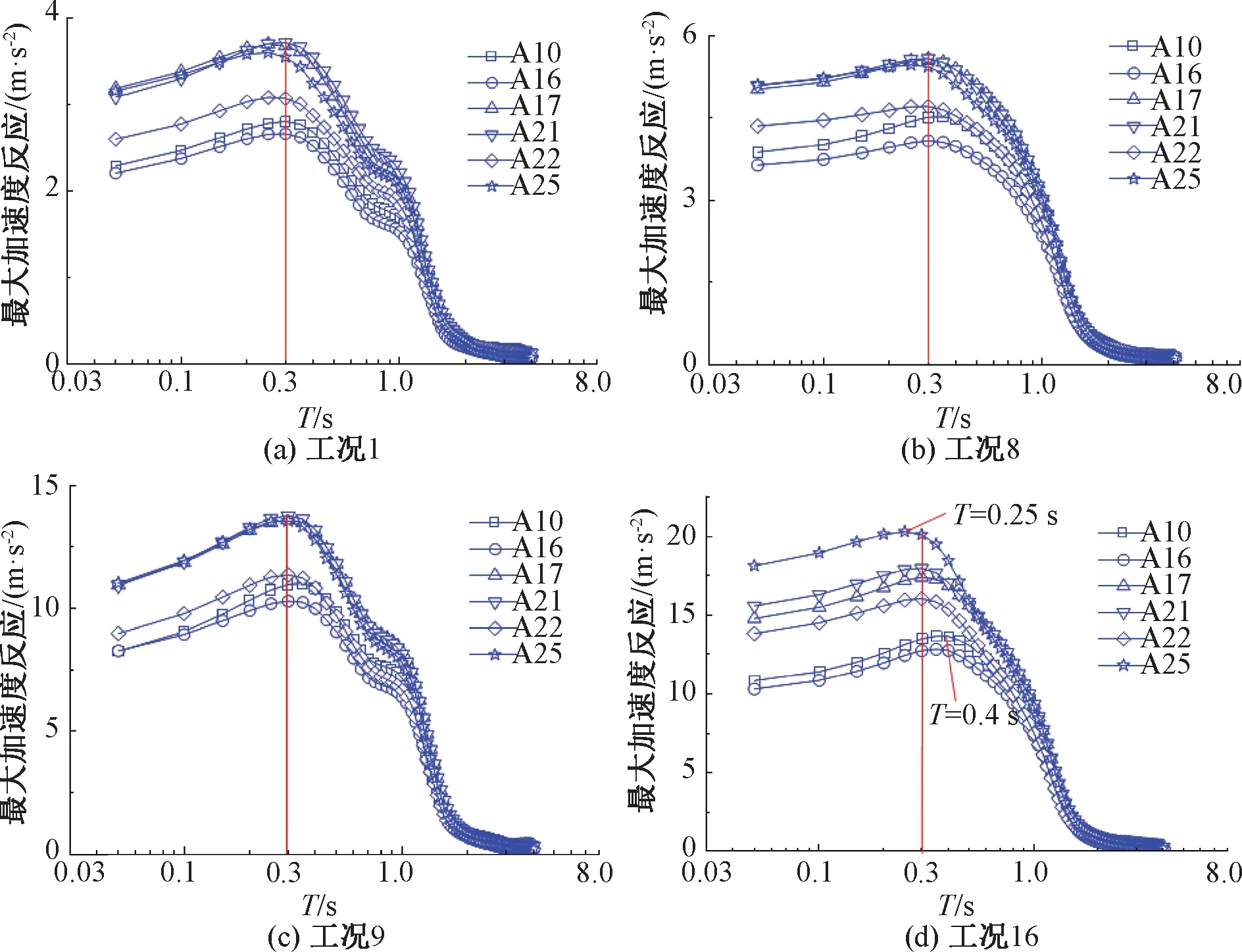
0 (1) 式中:k為分解層數;Ls為信號長度。 一般情況下地震波的持續時間為10~20 s,因此Ls取29~210,代入式(1),得出k為0~9,綜合考慮精細化和分辨率的要求后,本次試驗的加速度響應信號k值取3層為宜。由于試驗采用的地震波有效頻率為0.1~50.0 Hz,三次分解后得出第三層小波包共有23=8個。參考Shannon采樣定理[16],設定采樣頻率為100 Hz。小波包分解后的8個頻段范圍見表3。 表3 頻段序號及頻段范圍 因為具有良好的緊支撐性、光滑性及近似對稱性等優勢,選用Daubechies(db小波)作為基函數進行信號的小波包分解。按照階數,dbN小波基函數可分為db1~db10,試驗選用db5小波基函數即可滿足處理地震波信號的要求。利用Matlab,首先對加速度響應時程曲線進行Fourier變換,隨后對Fourier變換得到的頻譜信號進行小波包分解,然后對得到的各頻段信號重構,最后對各頻段進行能量占比的量化分析。 第一臺邊坡模型(模型一)試驗的失穩破壞過程屬于突發型,工況1~工況6(其中工況6X向輸入加速度峰值XA=0.233g)期間,邊坡上并未出現明顯裂縫或其他破壞現象,工況7(XA=0.235g)加載時,邊坡突然失穩破壞。在此后的加載工況中,坡腳、坡肩處進一步發生破壞,在工況10(XA=0.465g)的加載過程中,破壞更有加劇的趨勢。工況7(破壞)之前、工況7(破壞)之后及結束加載后的模型見圖2。 圖2 模型一(突發型) 第二臺模型(模型二)試驗存在裂縫產生到發展再到大變形的過程,屬于漸進型失穩邊坡。工況1~工況8(其中工況8輸入加速度峰值XA=0.235g)期間,邊坡上未觀察到明顯裂縫或其他損傷;工況9(XA=0.465g)加載過程中,坡面兩側中部靠上位置出現裂縫;此后,坡面裂縫逐漸發育,在工況16(XA=0.705g)加載結束后,坡面裂縫貫通,其他部位無明顯破壞;工況17(XA=0.935g)加載過程中,坡頂及其周邊坡面局部出現了一定數量的裂縫;在工況18(XA=1.050g)的加載過程中,邊坡失穩破壞,坡腳出現剪出面。邊坡模型失穩破壞過程見圖3。 圖3 模型二(漸進型) 排除采集有誤的測點數據(模型一的測點A7、模型二的測點A4、A7),繪制兩臺試驗所有測點PGA隨加載工況變化曲線,見圖4。 圖4 兩臺試驗PGA隨加載工況的變化趨勢 由圖4(a)可知,模型一(突發型)PGA隨著加載的進行,有兩次突變,分別出現在工況6(XA=0.233g)及工況10(XA=0.465g)的加載過程中。對邊坡模型失穩過程的觀察顯示,在工況6加載結束后,邊坡并未出現明顯裂縫或其他損壞,邊坡突然失穩是在工況7(XA=0.235g)的加載過程中發生的。在工況6加載時,雖然PGA值出現了突增現象,但是在邊坡上并未觀察到任何明顯的裂縫或損傷,隨后在工況7的加載中,邊坡突然失穩破壞,可推斷出在工況6加載結束后,邊坡內部的損傷已經完成了量變到質變的積累,已處于極限狀態。以極限狀態為界,可以將突發型失穩邊坡的失穩過程劃分為破壞前(工況1~工況5)、極限狀態(工況6)、破壞后(工況7~工況12)三個階段。 由圖4(b)可知,模型二(漸進型)隨著加載的進行,PGA只有一次突變,出現在工況17,該工況加載時邊坡裂縫恰好開始增多,變形明顯加快。漸進型失穩邊坡相較于突發型失穩邊坡,其地震失穩破壞過程較為緩慢,邊坡裂縫等損傷的發展易于觀察。與突發型失穩邊坡不同,漸進型失穩邊坡的失穩破壞過程不存在明顯的極限狀態分界點,而是有一個裂縫從出現、發展直至貫通的過渡階段。根據失穩破壞的特征,可將模型二(漸進型)的失穩過程暫時劃分為彈性變形階段(工況1~工況8)、塑性小變形階段(工況9~工況16)、大變形失穩破壞階段(工況17~工況18)三個階段。因為工況1~工況8沒有觀察到裂縫,暫時認為屬于彈性變形階段,在下文小波包部分進行論證。 因篇幅有限,為了在避免繁冗同時,達到反映整個失穩過程中小波包分量變化情況的目的,僅選取具有代表性的特征工況進行分析。對于模型一(突發型失穩),首先選取極限狀態對應的工況6,其次選取破壞前階段的工況1和工況5,以及破壞后階段的工況7和工況10;對于模型二(漸進型失穩),彈性變形階段選取工況1和工況8,塑性小變形階段選取兩端的工況9和工況16,以及大變形失穩階段僅有的工況17和工況18。 利用Matlab軟件編制程序對加速度響應信號進行小波包變換,得到各頻段的能量占比。第一頻段(0.10~6.25 Hz)的能量占比用E1表示,第二頻段(6.26~12.51 Hz)的能量占比用E2表示。經過分析發現,不管在哪個工況,各測點加速度響應信號的E1與E2之和均為90%左右,說明引起邊坡動力失穩破壞的主要是振動波低頻部分(0.10~12.51 Hz)。而且雖然各測點E1隨高程增加而減小,E2隨高程增加而增大,但E1始終大于50%,E2始終小于50%,說明主頻始終是第一頻段,次頻始終是第二頻段。繪制兩臺試驗各自特征工況下所有測點E1、E2與高程的散點圖,模型一、模型二分別見圖5、圖6(h為測點高程,H為坡高)。對應擬合曲線的結果見表4。 表4 E1和E2散點圖擬合公式及相關系數 圖5 模型一特征工況下E1和E2的高程規律 圖6 模型二特征工況下E1和E2的高程規律 由圖5可知,在破壞前(工況1~工況5),突發型破壞邊坡的E1和E2隨著高程的增加分別顯示出線性減小和線性增大的規律,隨著加載的進行,從工況6加載開始直到工況7,E1和E2的高程規律轉變為二次曲線型,說明在地震作用下,土體變形損傷不斷累積到一定程度后,引起了邊坡震動特性的改變,即3.2節提到的達到了極限狀態,在后續加載過程中邊坡突然失穩破壞。這驗證了對突發型失穩邊坡動力破壞過程的劃分,以極限狀態為界,可將突發型失穩邊坡的失穩過程劃分為破壞前、極限狀態、破壞后三個階段。 由圖6可知:與模型一相同,模型二在工況1至工況8,E1和E2隨高程的變化規律也分別表現出線性減小和線性增大的趨勢,即彈性變形階段;當加載至工況9時,E1和E2隨高程的變化規律由線性轉變為二次曲線,相應的,坡面開始出現裂縫,說明邊坡地震變形損傷過程過渡到了下一個階段,即塑性小變形階段,驗證了定義第一階段為彈性變形的假定;在后續的加載中,邊坡模型的損傷逐漸積累,但一直未發生整體失穩破壞,直到加載至工況17,開始發生大變形破壞。從工況9開始,E1和E2隨高程的變化規律一直是二次曲線型。 通過對比兩臺模型試驗的小波包分析結果可知,E1和E2隨高程的變化規律由線性進入非線性時,邊坡都出現了肉眼可見的破壞,從能量的變化規律,反映了在地震作用下邊坡損傷逐漸積累,直到其動力特性產生改變的過程。可以此為依據,判斷邊坡是否即將發生破壞。 兩臺模型的主要區別在于:模型一的坡腳為60°,坡度較陡,抗傾覆及抗滑移能力差,對邊坡損傷的允許值低,使得其地震失穩破壞是突然發生,且在大變形破壞前,基本無法通過肉眼觀察到土體的損傷變形;模型二則不同,其坡腳為45°,坡度交緩,在地震作用時,下部土體對上部土體具有一定的抗滑作用,即使局部產生微小裂縫,也不至于很快造成滑動面的貫通,能夠很好地“儲存”或釋放地震能量。坡度較緩的邊坡在出現大變形破壞前可以承受更多的變形損傷。 反應譜是指單自由度(單質點)體系在給定的地震作用下某個最大反應與體系自振周期的關系曲線,包括對加速度、速度和位移響應的反應譜分析。 在對加速度響應進行反應譜分析時,假設測點處土體是剛體單元,其加速度反應為 (2) 式中:ω為自振頻率;h為臨界阻尼;ωd為有阻尼的自振頻率;ug(t)為激勵加速度。 巖土體在地震作用下,土體內的損傷會不斷積累,原有的微結構隨之破壞,從而改變巖土體的固有頻率或周期T,引起加速度響應的變化。因此,基于反應譜的巖土體地震研究需要注意特征周期T和反應譜幅值的變化。反應譜是基于彈性結構的地震動力反應繪制的,仍然把地震力作為靜力對待,雖然引入了結構影響系數進行改進,但是只能得到土體結構進入彈塑性狀態的整體反應,無法進行巖土體結構的精細化分析。因此,本文只對模型試驗彈塑性小變形階段進行分析。 為了便于分析,試驗一對坡面測點A2、A3、A4、A5、A6隨機選取極限狀態前工況2、工況3、工況5、工況6進行分析,試驗二對坡面的A10、A16、A17、A21、A22、A25測點取塑性小變形階段的工況1、工況8、工況9、工況16進行分析。 出現最大值的反應譜曲線對應的周期即為特征周期,由圖7可知,模型一(突發型失穩),在加載至極限狀態(工況6)之前,反應譜曲線顯示其特征周期均為0.3 s,輸入地震波強度的增加對反應譜幅值增益效果并不明顯。加載至極限狀態(工況6)時,邊坡上部測點的特征周期變為0.2 s,邊坡下部測點的特征周期變為0.35 s,反應譜幅值由3 m/s2劇增至9 m/s2。 圖7 模型一坡面測點反應譜 由圖8可知,模型二(漸進型失穩),隨著工況9的加載,邊坡進入塑性小變形階段,反應譜幅值發生突變,但特征周期并未發生明顯變化,保持在0.3 s。直至加載至工況16,即將進入大變形階段,邊坡上部測點的特征周期變為0.2 s,邊坡下部測點的特征周期變為0.4 s。 圖8 模型二坡面測點反應譜 對兩臺試驗的反應譜分析表明,特征周期直觀反映了邊坡模型土體特性隨震動損傷積累的變化,在整個試驗過程中,兩臺邊坡模型的特征周期的變化范圍在0.2~0.4 s之間,即2.5~5.0 Hz,包含在前文小波包變換得到的第一頻段(主頻)范圍0.10~6.26 Hz之內,反應譜與小波包分析結果互為補充驗證。 (1)無論邊坡失穩形態如何改變,地震波低頻成分(0.10~12.51 Hz)起主導作用,第一頻段(0.10~6.26 Hz)能量占比E1隨著高程的增加逐漸減小,第二頻段(6.26~12.51 Hz)能量占比E2隨著高程的增加逐漸增大,但是主頻始終是第一頻段,能量占比E1始終大于50%。 (2)PGA的突變,邊坡E1和E2隨高程的變化規律由線性到非線性的轉變,標志著邊坡損傷積累由量變到質變的轉化,可作為邊坡開始大變形破壞的依據。 (3)突發型失穩邊坡的反應譜特征周期與幅值的突變是同步的,標志著邊坡即將進入極限狀態;漸進型邊坡的特征周期與反應譜幅值的突變不同步,反應譜幅值的突增標志著塑性小變形開始發生,特征周期的突變預示著邊坡大變形破壞的發生。 (4)通過對邊坡失穩破壞過程的觀察以及對PGA、小波包變換、頻譜分析數據的對比分析,可將突發型失穩邊坡的地震動力失穩過程劃分為破壞前、極限狀態、破壞后三個階段,將漸進型破壞邊坡的失穩過程則劃分為彈性變形、塑性小變形和大變形失穩破環三個階段。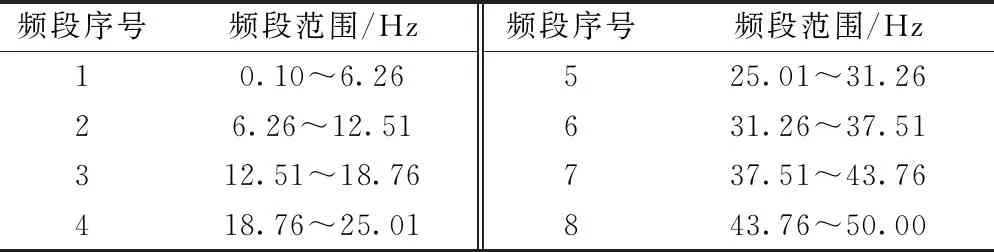
2.2 小波包基函數選取
3 模型試驗分析
3.1 邊坡模型的失穩破壞過程分析


3.2 失穩過程中PGA的表現
3.3 響應加速度的小波包分析

3.4 反應譜分析
4 結論

