談?wù)勄蠛瘮?shù)解析式的兩個(gè)常用路徑

劉志誠

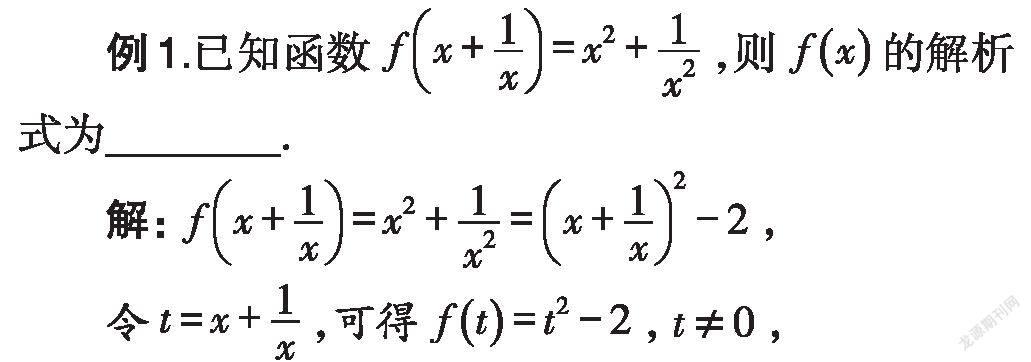
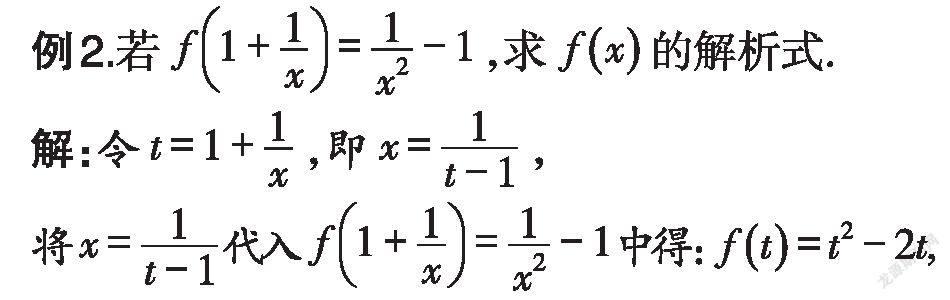
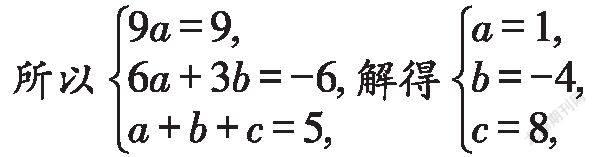
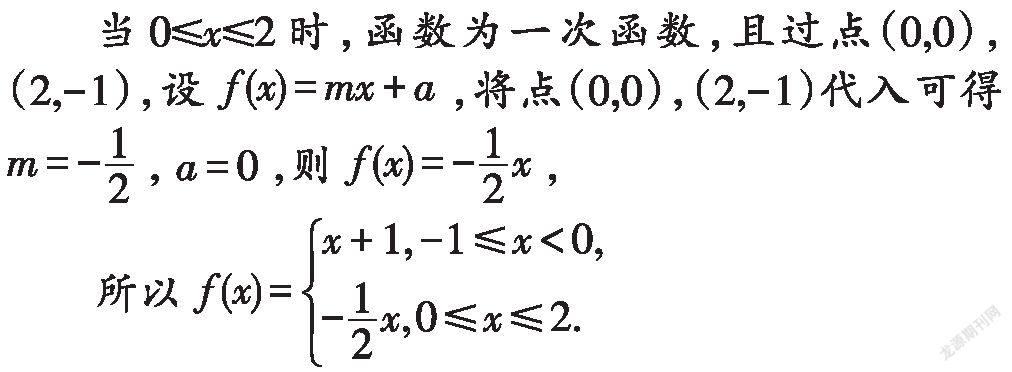
函數(shù)的解析式是表示函數(shù)的重要方法.求函數(shù)的解析式問題的難度一般不大，通常會(huì)要求根據(jù)函數(shù)的性質(zhì)、點(diǎn)的坐標(biāo)、已知關(guān)系式來求函數(shù)的解析式.那么，如何進(jìn)行求解呢？下面介紹兩種求函數(shù)解析式的途徑：換元和引入待定系數(shù).

一、換元

換元法是求函數(shù)解析式的常用方法.若已知復(fù)合函數(shù)f（g（x））的表達(dá)式，要求函數(shù)f（x）的解析式，可通過添項(xiàng)、拆項(xiàng)、變系數(shù)、湊因子等手段將f（g（x））的表達(dá)式配湊成g（x）的倍數(shù)或平方式，再將g（x）用x替換，通過換元便可求得f（x）的解析式.

所以函數(shù)f（x）的解析式為：f（x）=x-2，x≠0.

有時(shí)，我們無法將復(fù)合函數(shù)f（g（x））的表達(dá)式配湊為g（x）的倍數(shù)或平方式，此時(shí)可令g（x）=u，求得x=g（u），然后將其代入f（g（x））的表達(dá)式中，便可將函數(shù)式轉(zhuǎn)化為關(guān)于u的函數(shù)式，再令u=x，即可得到函數(shù)f（x）的解析式.

令t=x，可得函數(shù)f（x）的解析式為f（x）=x-2x.

二、引入待定系數(shù)

當(dāng)已知函數(shù)f（x）的類型，如指數(shù)函數(shù)、對(duì)數(shù)函數(shù)、反函數(shù)等時(shí)，可以直接利用待定系數(shù)法求函數(shù)f（x）的解析式.首先設(shè)出函數(shù)的解析式，若f（x）是二次函數(shù)，則設(shè)f（x）=ax+bx+c（a≠0）;若f（x）是冪函數(shù)，則設(shè)f（x）=x……然后根據(jù)題目中的已知信息，如點(diǎn)的坐標(biāo)、已知關(guān)系式等建立關(guān)于待定系數(shù)的方程，通過解方程或方程組求得待定系數(shù)的值，這樣就能得到函數(shù)的解析式.

例3.若f（x）為二次函數(shù)，且f（3x+1）=9x-6x+5，求f（x）的解析式.

解：設(shè)f（x）=ax+bx+c（a≠0），

因此f（3x+1）=a（3x+1）+b（3x+1）+c=9ax+（6a+3b）x+a+b+c，

因?yàn)閒（3x+l）=9x-6x+5，

因此函數(shù)f（x）的解析式為f（x）=x-4x+8.

函數(shù)f（x）為二次函數(shù)，于是設(shè)f（x）=ax+bx+c（a≠0），根據(jù)已知關(guān)系式建立恒等式，此時(shí)恒等式兩邊各項(xiàng)的系數(shù)必然相等，據(jù)此建立關(guān)于系數(shù)的方程組，通過解方程組來求得問題的答案.

例4.若函