怎樣選擇合適的方法來求函數的解析式

周必輝

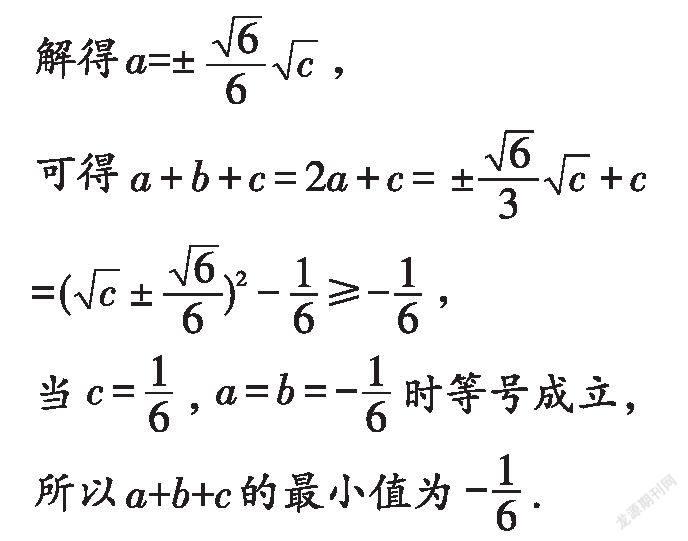
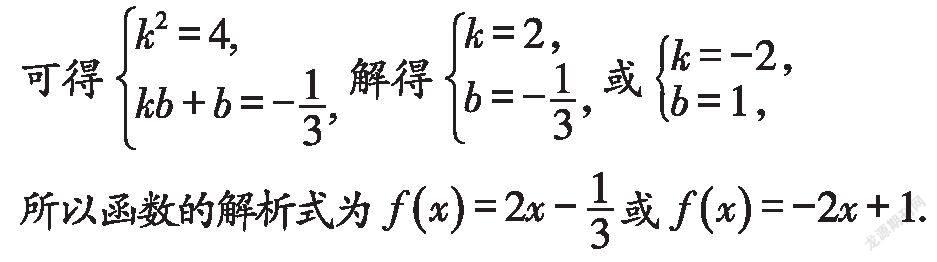
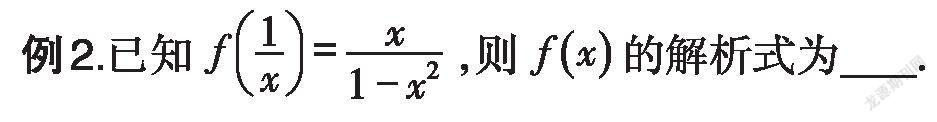
求函數的解析式問題主要考查函數的定義域、基本函數的圖象、性質.此類問題的難度不大，在解題時只要能選擇合適的方法，便能快速求得問題的答案.

一、待定系數法

待定系數法是指將多項式表示成另一種含有待定系數的新形式，進而得到一個新的恒等式，根據恒等式的性質得到系數應滿足的方程或方程組，然后通過解方程或方程組，求出待定的系數或找出這些系數應滿足的關系式.運用待定系數法求函數的解析式，需先根據函數的類型，引入待定系數，設出函數的解析式，再把題設中的條件代入，建立方程（組），求得待定系數的值，即可求得函數的解析式.

例1.已知f（x）是一次函數，且f（f（x））=4x-1，求f（x）的解析式.

分析：由于函數的類型已確定，所以只需根據一次函數的表達式，引入待定系數k、b，設出函數的解析式f（x）=kx+b（k≠0，b為常數），根據題意建立方程或方程組，求得待定系數k、b的值，即可求得函數的解析式.

解：設f（x）=kx+b（k≠0），

則f（f（x））=f（kx+b）=k（kx+b）+b

=kx+kb+b=4x-1，

利用待定系數法求函數的解析式，需熟練掌握各類基本函數的表達式，這樣才能引入合適的待定系數，設出正確的函數解析式.

二、換元法

換元法是將代數式中的某一部分用一個或幾個新的變量替換的方法.換元法主要適用于求解代數式較為復雜或復合函數的解析式問題.在解題時，可將代數式的某一部分或復合函數f（g（x））中的g（x）用一個新元替換，得到關于新元的式子，再將新元用x替換，就能得到函數f（x）的解析式.

運用換元法求函數的解……