解答圖形平移問題的幾個步驟

劉冬華

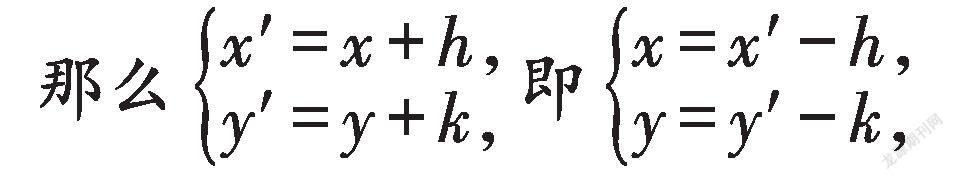
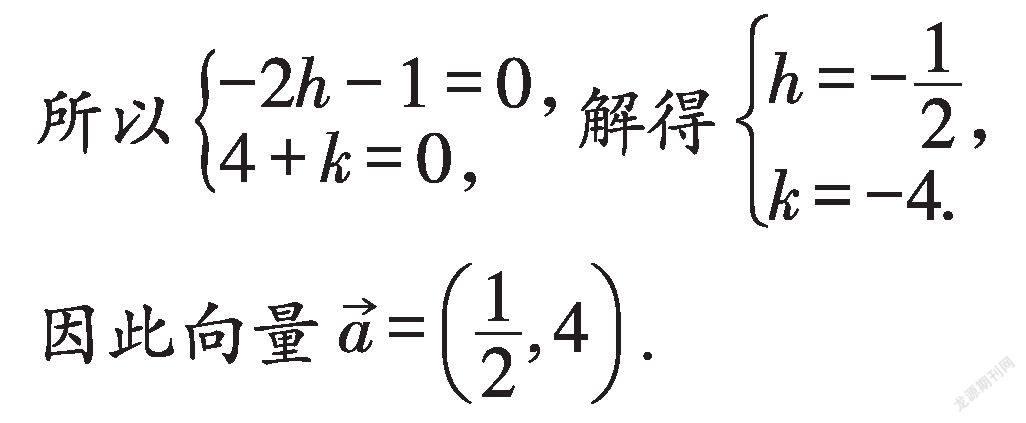
圖形平移問題經常出現在各類試題中，其常見的命題形式是：將某一圖形按某一向量平移，或沿著x、

y軸平移a個單位長度，求平移前后函數的解析式、點

的坐標、向量的坐標.解答此類問題，需根據圖形平移

變換公式，借助圖形來分析問題，其基本步驟是：

1.確定初始函數的圖象、曲線的大致形狀;

2.明確需平移向量的大小和方向，以及沿著x或

y軸平移的單位長度;

4.通過計算求得問題的答案.

則點A′的坐標為A′（7，3）.

同理可得，B（6，7）平移后所對應的點的坐標為B′（10，8）.

解：設拋物線F上的一點為P（x，y），且該點在拋物線尸上的對應點為P′（x′，y′）.

將其代入y=3x+6x+6中，得：y+3=3（x-1）+6（x-1）+6.

將其整理得：y=3x，

因此，拋物線F的解析式為y=3x.

雖然圖形經過平移后各個點的相對位置、圖形的形狀都不發生改變，但是各個點的坐標會發生改變.平移后的點的坐標可根據平移變換公式求得，將其對應的點的坐標代入已知曲線的方程中，即可求得變換前后的曲線方程.

將其代入函數y=log（2x-1）+4，

可得y′-k=log（2x′-2h-1）+4，

即y′=log（2x′-2h-1）+4+k.

因為平移后的函數解析式為y=log2x，

在解題時，首先要根據題目中的信息，確定需進

行平移的點或圖形以及平移的向量，設出未知的點或者向量，再根據平移變換公式列出方程組，解方程組便可求得問題的答案.

總之，解答圖象平移問題，需明確平移前后哪些量不改變，哪些量改變了，并建立各個點的坐標之間的對應關系，然后結合圖形，根據平移變換公式進行求解.