求解平面向量問題的兩種常用思路

蔡麗軍

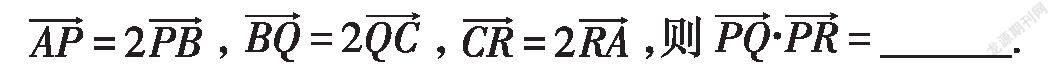
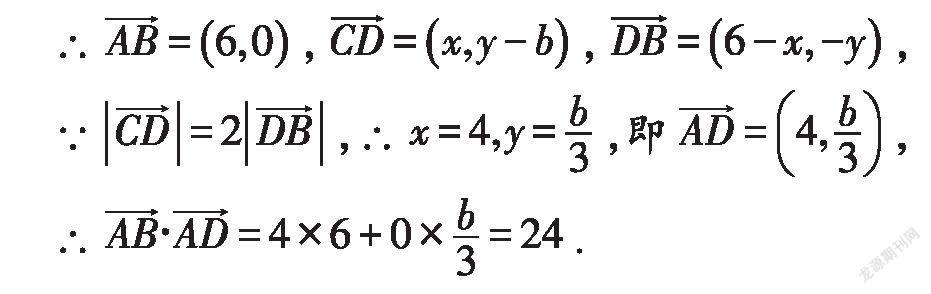
平面向量是高中數學中的重要內容，平面向量問題經常出現在各類試題中.此類問題側重于考查平面向量的運算法則、基本定理.解答平面向量問題的常用思路主要有利用基底法和坐標法.下面結合實例進行探討.

一、采用基底法

由平面向量的基本定理可知，平面內的任意一個向量都可以由兩個基底向量表示出來，因而基底法是解答平面向量問題的重要方法.運用基底法求解平面向量問題的思路是：①根據問題中所給的條件，選取一組向量作為基底向量;②用基底向量表示所求的向量;③運用平面向量的數乘運算法則、加法法則、減法法則、數量積公式、模的公式等進行運算，求得結果。

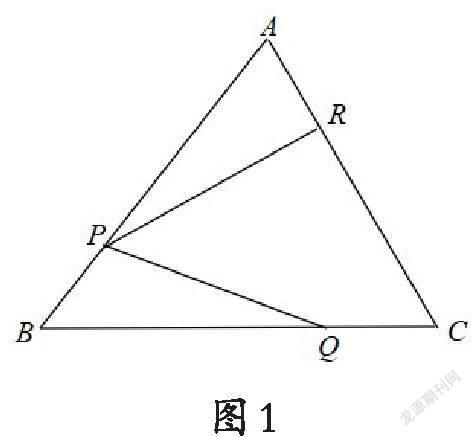
例1.如圖1，已知正三角形ABC的邊長為3，

的答案.

二、利用坐標法

有些平面向量問題中的圖形為規則圖形，如正方形、矩形、正三角形、直角梯形等，可根據幾何圖形的特點，尋找垂直關系，建立平面直角坐標系，再求出各個向量的坐標，就能根據向量的坐標運算法則來解題.

以例1為例.

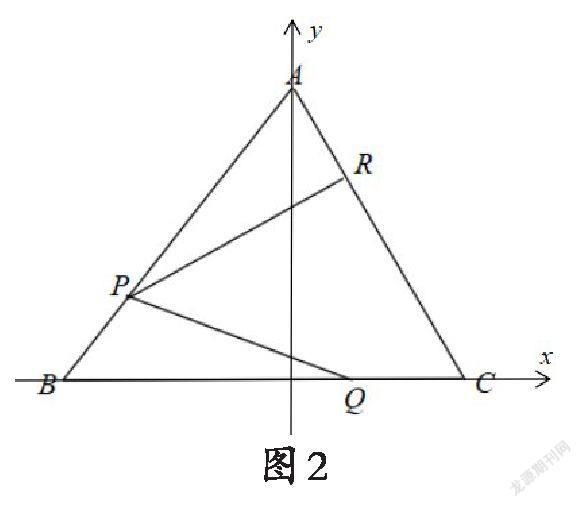
根據正三角形的特征，以BC所在的直線為x軸，BC的中垂線為y軸建立平面直角坐標系，便可采用坐標法求得各個點、向量的坐標，根據向量的坐標運算法則求解即可.

可得B（6，0），設點C（0，b），D（x，y），

可見，運用坐標法解題，關鍵是根據圖形的特點，建立合適的平面直角坐標系.

相比較而言，基底法的適用范圍較廣，但較為繁瑣;坐標法較為簡單，但其適用范圍較窄，兩種方法各有千秋.同學們應熟練掌……