模糊PID神經網絡逆控制多電機系統研究

唐友亮 張錦

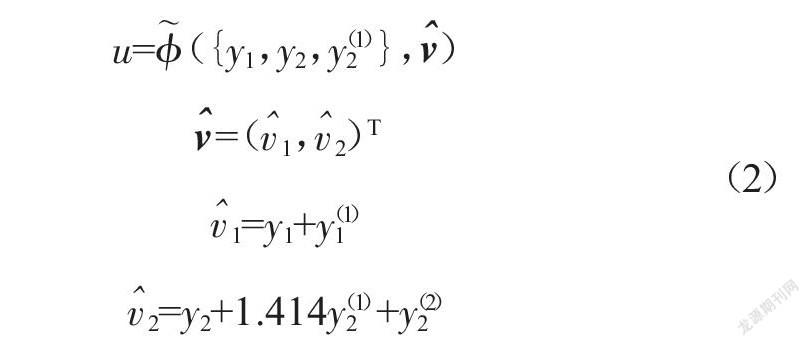
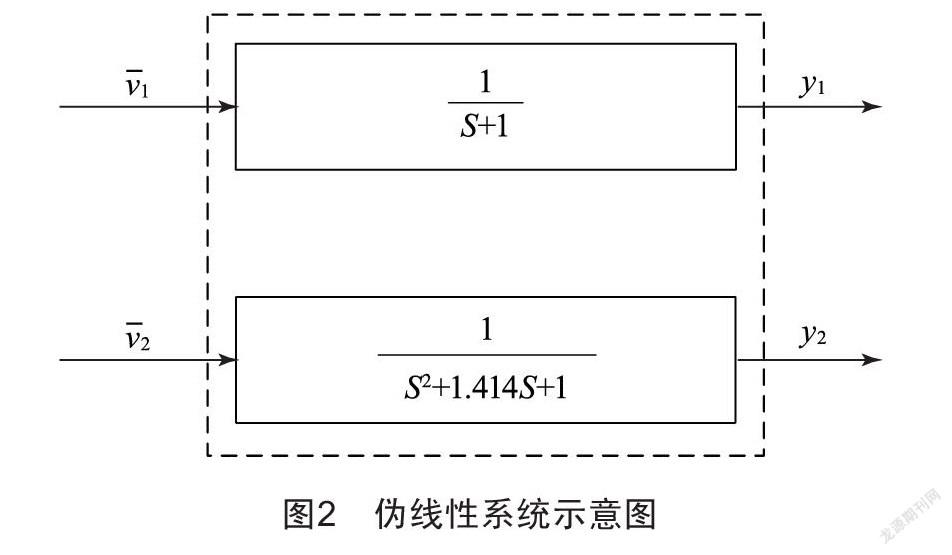
摘 要：基于多電機協同控制系統非線性強耦合特性，構建了一種模糊PID神經網絡逆系統控制方法。采用神經網絡算法擬合多電機控制系統廣義逆模型，由此得到復合后的偽線性系統，該偽線性系統實現了系統的線性化解耦。模糊PID控制既可作為閉環控制器整定偽線性系統的建模誤差，又可實現在線自適應控制，解決了傳統閉環控制不方便實時控制的問題。

關鍵詞：多電機;神經網絡;逆系統;模糊PID

中圖分類號：TM30? 文獻標志碼：A? 文章編號：1671-0797（2022）13-0012-04

DOI：10.19514/j.cnki.cn32-1628/tm.2022.13.004

0??? 引言

由于工業生產技術的不斷發展，生產線變得愈加龐大和復雜。受電機功率制約，傳統的單電機控制模式已難以滿足很多現代工業自動化場合的生產需求，因而由多臺電機協同控制已成為必然趨勢，尤其是在印花、經紗、軋鋼、造紙、薄膜等需要批量生產的現代工業領域[1-3]。多交流電機系統是一種具備高階性、強耦合性、非線性等特點的復雜控制對象，較難得到其精準的數學模型，而傳統的PID控制難以達到令人滿意的控制效果;另外，工業生產實踐中需要實現速度和張力的解耦以及外界突變情況的實時調整，這就進一步增加了控制難度。

因此，如何高性能地控制此種多變量、非線性、強耦合、隨變系統已成為當今的研究熱點[4]。

因不受非線性模型制約，逆系統方法在非線性控制領域有所應用[5];而神經網絡的主要特點是不依賴于被控系統的精確數學模型，適用于一般非線性系統，對系統參數結構變化控制具有較強的魯棒性[6]。因此，神經網絡逆系統方案可解決線性化及解耦問題。對于解耦后的偽線性系統，其建模誤差需要通過閉環控制器解決，常用的PID控制其動態參數調整較為復雜，實時性較差，而作為閉環控制器的模糊PID控制能夠很好地解決這一問題[7-8]。

本文以兩電機變頻系統為基礎，構建兩電機神經網絡逆系統，進而引入模糊PID控制，并對其進行仿真試驗研究。

1??? 兩電機逆系統模型

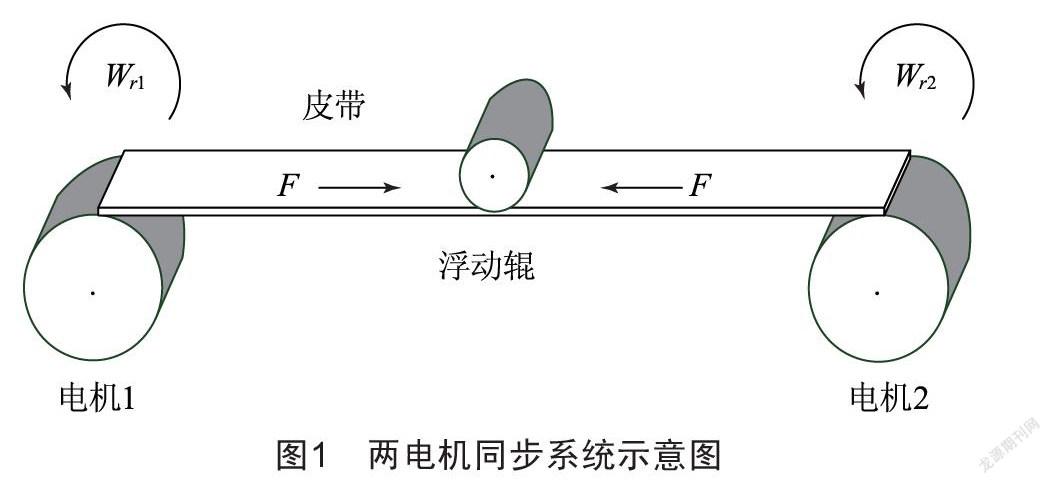
對于兩電機同步系統，其速度與張力示意模型如圖1所示。

在磁通穩定的前提下，該系統數學模型表述為[9]：

=f（x，u）=（u1-x1）？鬃2 r1-（TL1+r1x3）（u2-x2）？鬃2 r2-（TL2-r2x3）r1k1x1-r2k2x2-，y=h（x）=[y1，y2]T=[x1，x3]T=[ωr1，F]T（1）

式中：下標1、2分別表示第一、二臺電機;np為電機極對數;J為轉子轉動慣量;Tr為電磁時間常數;Lr為轉子自感;？鬃r為轉子磁鏈;TL為負載轉矩;k、r為皮帶輪的速比、半徑;K為傳遞函數;T為張力變化常數;ωr為電氣角速度;F為皮帶張力。

其中，狀態變量x=[x1，x2，x3]T=[ωr1，ωr2，F]T;控制變量u=[u1，u2]T=[ω1，ω2]T。

根據逆系統理論[10]，可證得該系統相對階等于其向量本性階，因此該系統可逆，其廣義逆可表示為：

u=（{y1，y2，y2 （1）}，）

=（1，2）T

1=y1+y1 （1）

2=y2+1.414y2 （1）+y2 （2）

所得兩電機逆系統模型與原系統結合，從而得到一個偽線性系統，由此線性化解耦為一個簡單的一階系統和一個最佳二階系統，如圖2所示。

2??? 兩電機神經網絡逆控制策略的構建

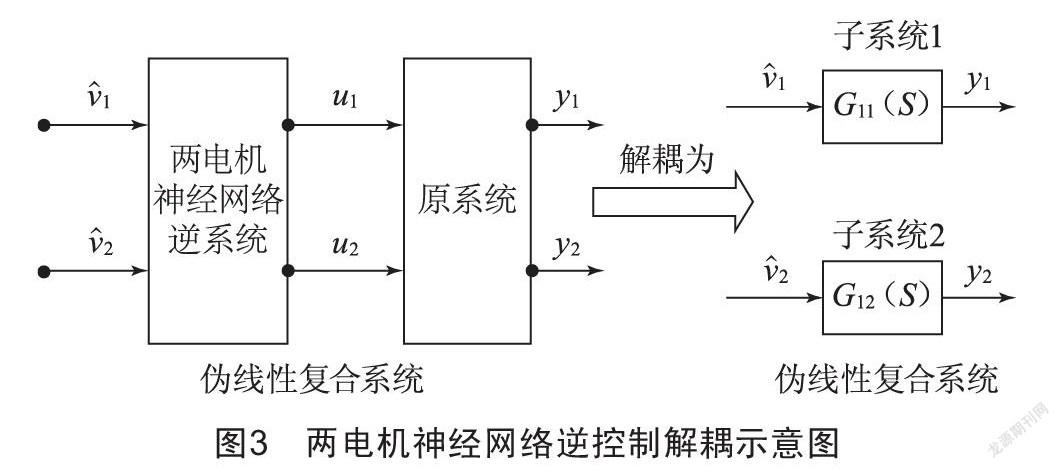
神經網絡具備非線性逼近能力、自學習能力、容錯能力良好等一系列特點[11-12]。借助于神經網絡實現擬合后的逆系統，再將該逆系統串接于原系統前，從而構成兩電機神經網絡逆偽線性控制系統。

兩電機神經網絡逆控制構建的偽線性系統解耦為單輸入單輸出子系統的極點在復平面內通過合理配置，形成穩定的子系統，得到較為理想的偽線性復合系統，如圖3所示。

由此可知，在構建兩電機神經網絡逆控制策略時需要注意以下幾個方面：

（1）選定合適的網絡結構，并確定所用神經網絡的輸入、輸出節點數量。

（2）激勵信號要采樣充分，選擇包含整個試驗范圍的數據，從而確保訓練采樣準確。

（3）要保證神經網絡離線訓練的準確度，進而可實現兩電機同步系統外部特性的神經網絡逆系統。

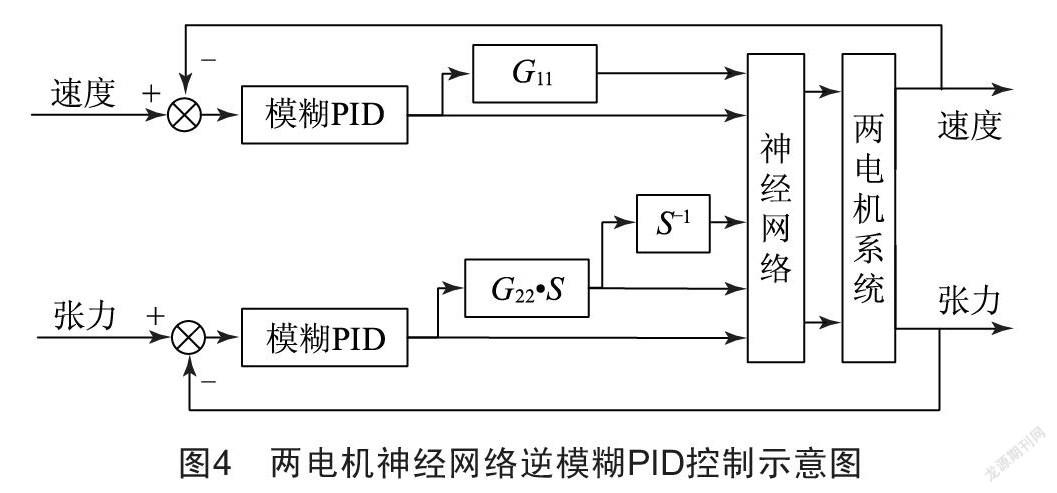
3??? 兩電機神經網絡逆模糊PID控制實現

由兩電機神經網絡逆系統構建的偽線性系統解決了線性化解耦問題，其開環系統存在的些許建模誤差需要設計閉環控制器加以控制。傳統PID控制方法應用非常廣泛，但其不具備動態適應能力，當外界條件發生改變時，其動態控制性能難以保證。

模糊控制是目前控制領域有廣泛應用空間的一種非線性控制策略，其根據模糊規則進行模糊推理，從而實現被控對象的模糊控制。模糊控制構建的控制系統具有較強的魯棒性，在線性、時變、滯后系統控制中具備較大優勢。

將模糊控制與傳統PID控制技術相結合可以構成多種模糊PID控制器，其具備兩種控制算法的特點。基于一系列模糊判定規則，系統自動調整PID參數，實現原系統智能化PID控制，兩電機神經網絡逆控制系統在運行過程中隨輸入條件變化、受干擾因素影響時，也將實現在線辨識系統特征參數，實時改變控制參數，從而使控制系統始終保持動態最優控制。

兩電機神經網絡逆偽線性系統具有開環穩定的線性傳遞關系，但神經網絡在擬合原系統時會存在些許誤差，是不完全線性化的，因此加上模糊PID閉環控制器，從而構成兩電機神經網絡逆模糊PID控制系統，如圖4所示。

4??? 仿真驗證

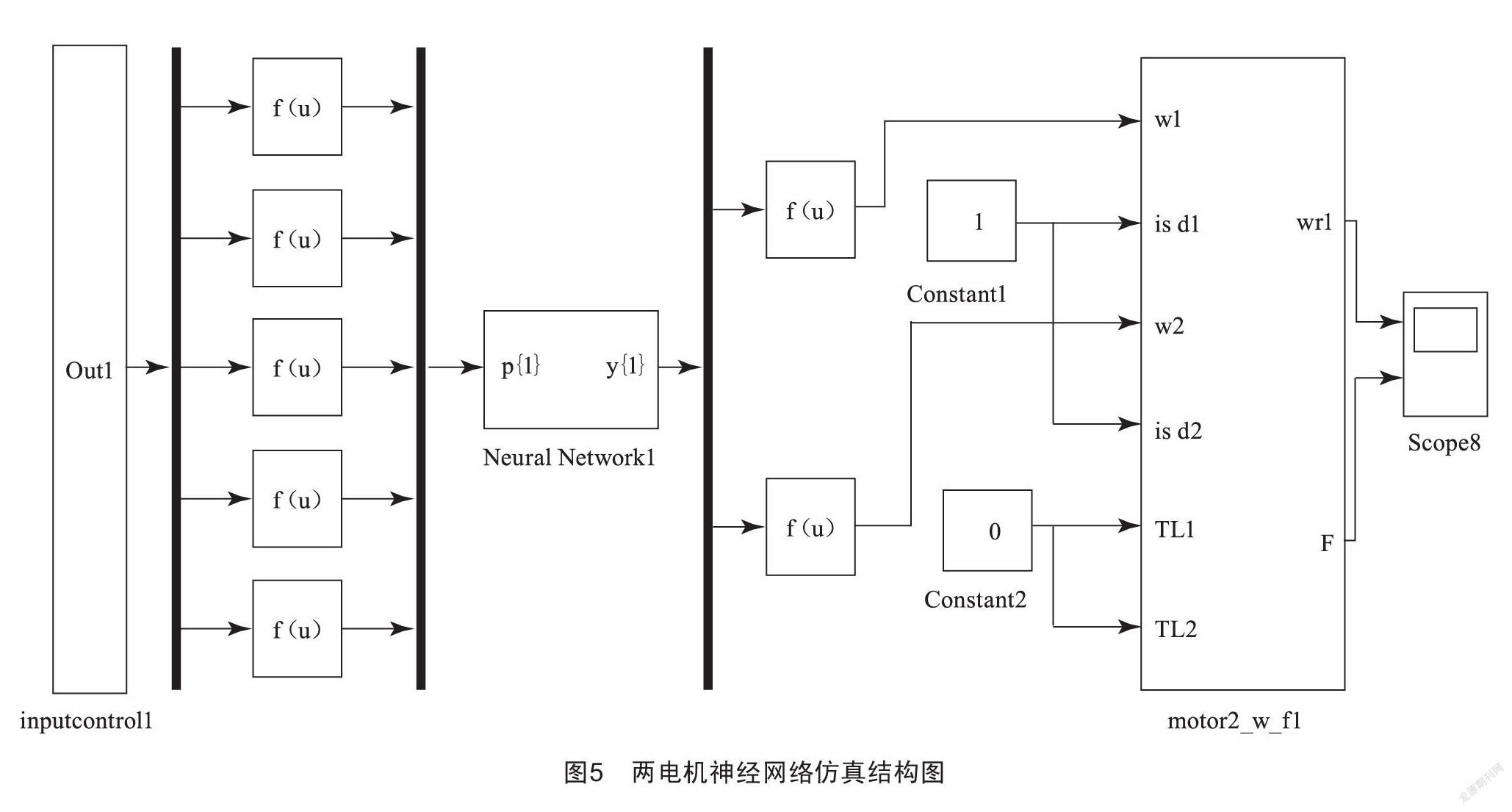
采用Matlab/Simulink構建模糊PID神經網絡逆控制多電機系統進行驗證。把采樣信號y1、（y1+1）、y2、2、（2+

1.4142+y2）作為神經網絡的輸入（y=h（x）=[y1，y2]T=[x1，x3]T=[ωr1，F]T），u1、u2作為神經網絡的輸出（u=[u1，u2]T=[ω1，ω2]T），并進行歸一化處理后訓練神經網絡。神經網絡輸入、輸出仿真結構如圖5所示。

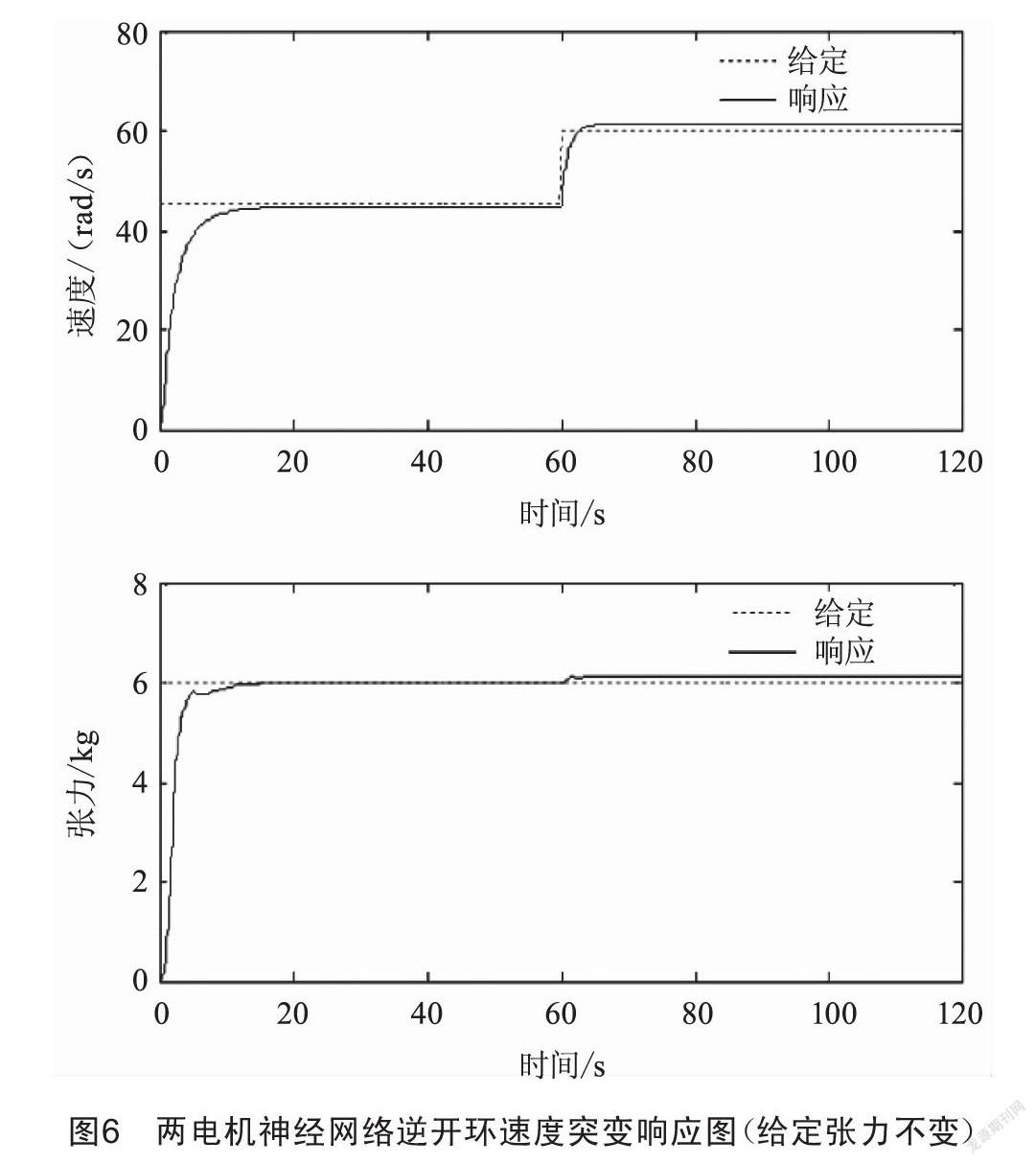
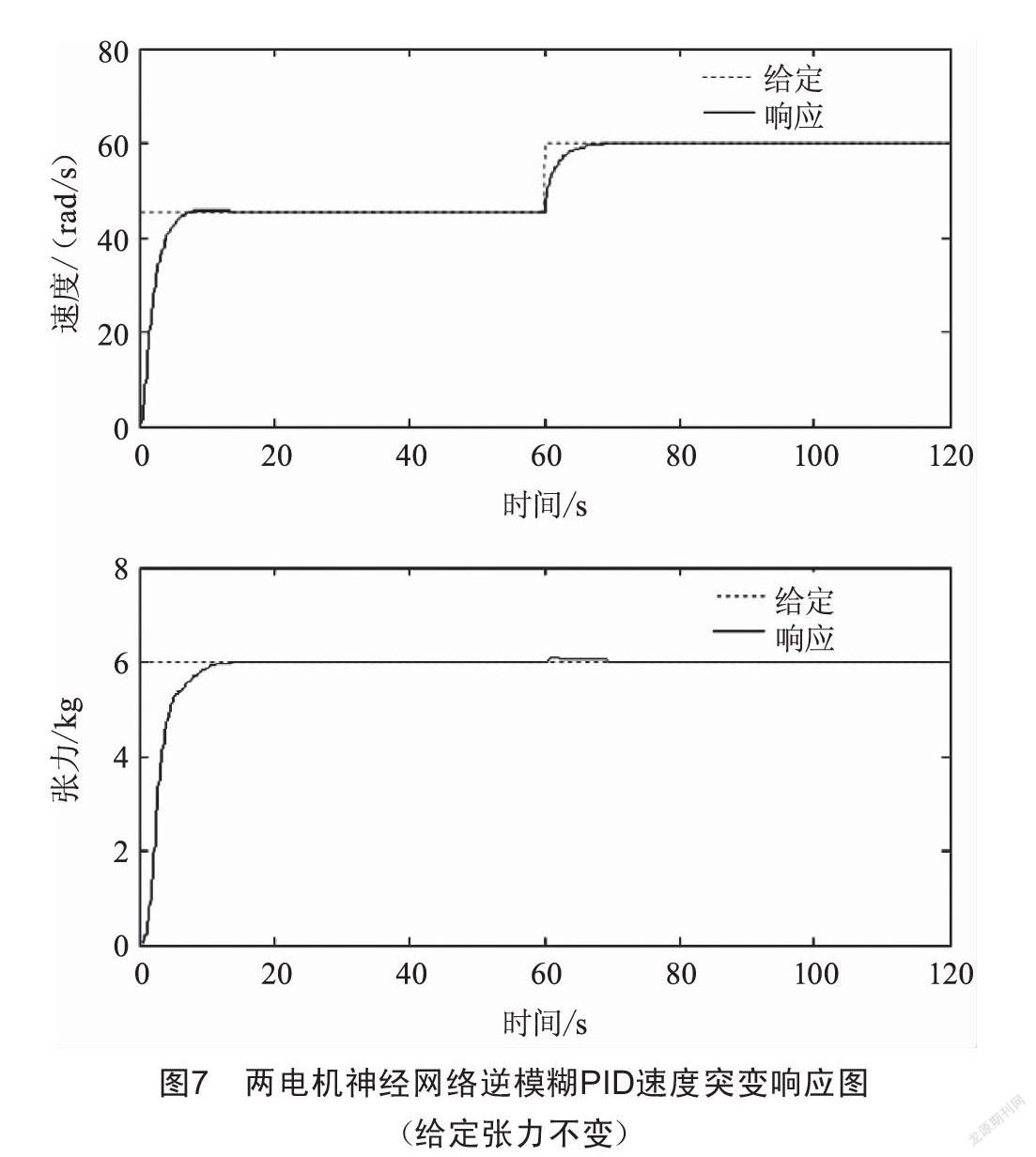
圖6、圖7分別為轉速由45 rad/s突增至60 rad/s，張力給定6 kg不變時，兩電機神經網絡逆開環及兩電機神經網絡逆模糊PID控制下速度突變時的系統響應波形。

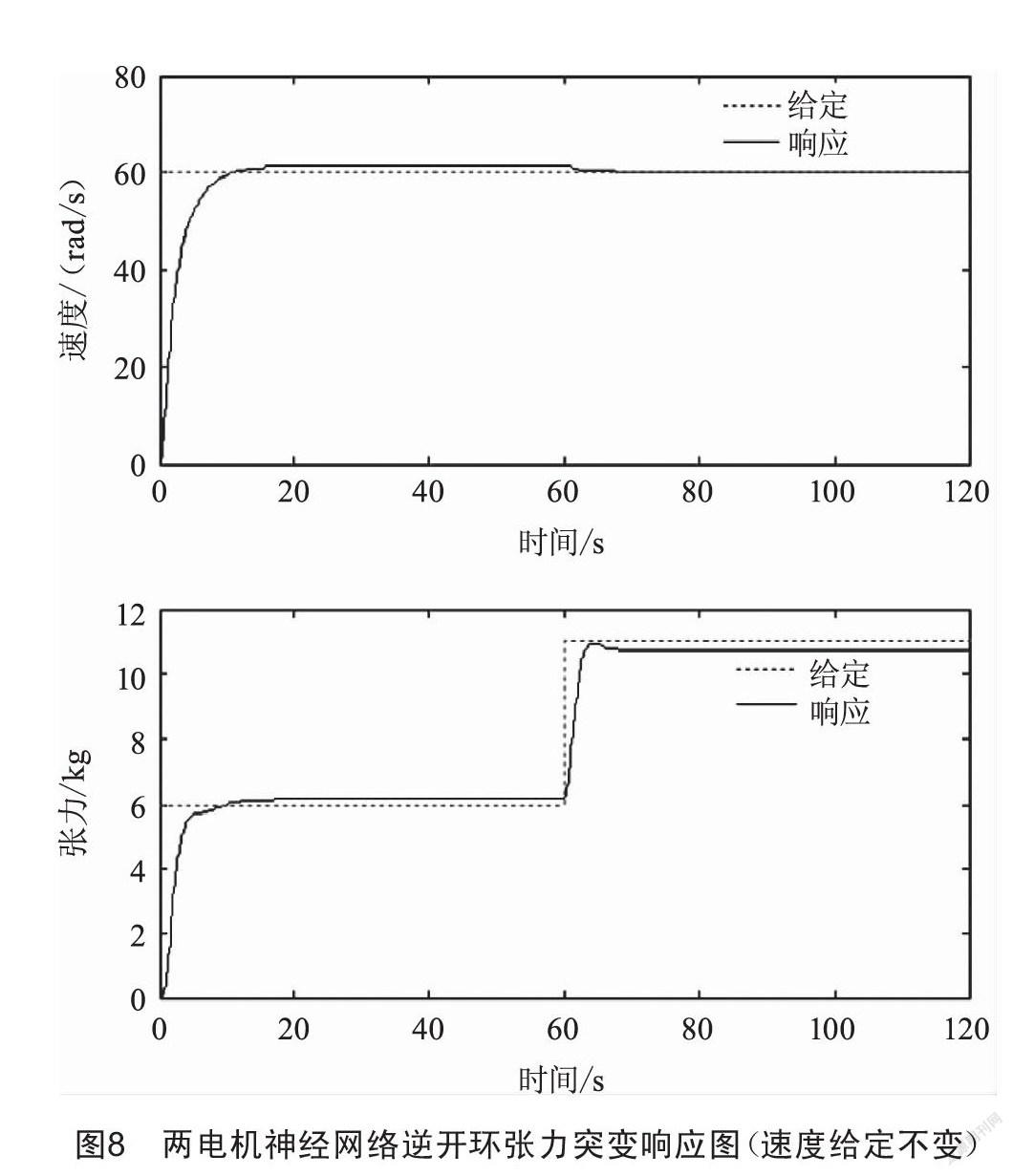
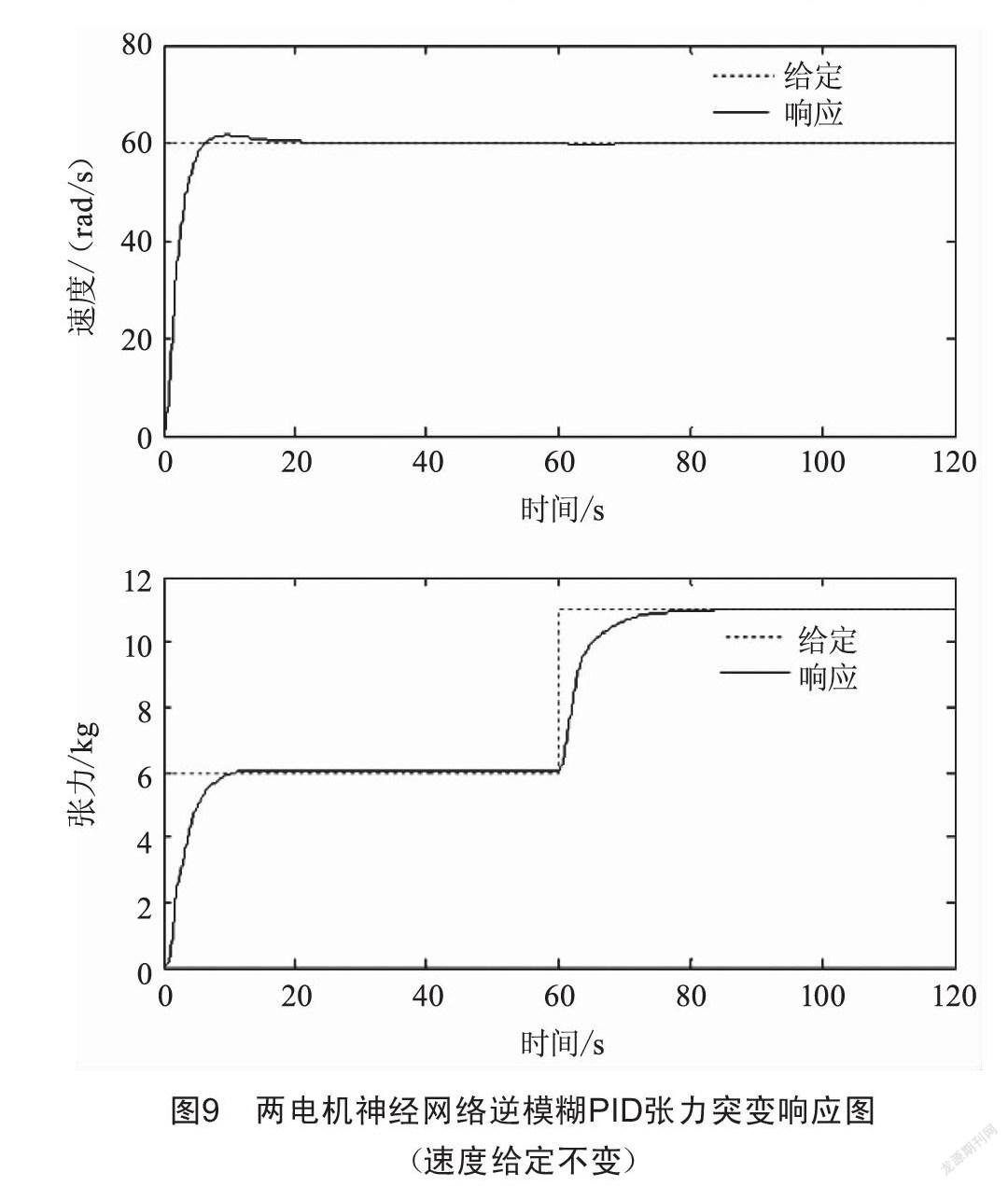
圖8、圖9分別為張力由8 kg突增至11 kg，速度給定60 rad/s不變時，兩電機神經網絡逆開環及兩電機神經網絡逆模糊PID控制下張力突變時的系統響應波形。

由以上仿真波形可以看出，兩電機神經網絡逆控制方法能夠很好地實現線性化解耦，無論是速度突變還是張力突變，都可以很好地保持系統相對穩定，但兩電機神經網絡開環控制會存在一些穩態誤差，當引入模糊PID閉環控制時，穩態誤差消除，兩電機神經網絡逆模糊PID控制體現出了很好的動態響應特性及魯棒性。

5 ?? 結論

本文構建了兩電機神經網絡逆系統與模糊PID相結合的控制方案，由仿真結果可得以下結論：

（1）兩電機神經網絡逆控制在線性化解耦方面性能突出，并可保持開環穩定。

（2）兩電機神經網絡逆開環控制會存在一定的穩態誤差，此誤差由神經網絡擬合兩電機逆系統時形成。

（3）兩電機神經網絡逆模糊PID控制可以很好地保證系統速度和張力的解耦，此外，對于偽線性化后的速度和張力子系統閉環穩定，具有很好的動態適應性。

[參考文獻]

[1] KONG W K，WANG J X，KONG D W，et al.Motor shifting and torque distribution control of a multi-motor driving system in electric construction vehicles[J].Advances in Mechanical Engineering，2021，13（6）：1-11.

[2] 耿強，王少煒，周湛清，等.改進型偏差耦合多電機轉速同步控制[J].電工技術學報，2019，34（3）：474-482.

[3] DHADEKAR D D，TALOLE S E.Robust fault-tolerant flight control of quadrotor against faults in multiple motors[J].Proceedings of the Institution of Mechanical Engineers，Part G：Journal of Aerospace Engineering，2021，235（16）：095441002199954.

[4] 楚曉艷，年曉紅，劉靜靜.基于魯棒滑模觀測器的多電機卷繞系統故障檢測和隔離[J].控制理論與應用，2018，35（6）：795-804.

[5] 朱熀秋，曹莉，李衍超，等.基于最小二乘支持向量機逆系統的五自由度無軸承同步磁阻電機解耦控制[J].中國電機工程學報，2013，33（15）：99-108.

[6] 張福生，潘學文，路超.基于SSA優化BP神經網絡的故障診斷系統研究[J].中國工程機械學報，2022，20（1）：81-85.

[7] SALL M，KEBE A，GUEYE I，et al.Comparative study between the PID regulator and the fuzzy regulator applied to the operation of a brushless DC motor[J].Energy and Power Engineering，2021，13（11）：365-376.

[8] 何青，孟岳.基于二型模糊變積分PID控制的BLDCM控制研究[J].控制工程，2021，28（8）：1691-1699.

[9] 劉國海，康梅，尤德同，等.兩電機同步系統的神經網絡逆控制[J].江蘇大學學報（自然科學版），2006（1）：67-70.

[10] 劉國海，張錦，趙文祥，等.兩電機變頻系統的支持向量機廣義逆內模解耦控制[J].中國電機工程學報，2011，31（6）：85-91.

[11] 蔡瑞初，謝偉浩，郝志峰，等.基于多尺度時間遞歸神經網絡的人群異常檢測[J].軟件學報，2015，26（11）：2884-2896.

[12] 林景棟，吳欣怡，柴毅，等.卷積神經網絡結構優化綜述[J].自動化學報，2020，46（1）：24-37.

收稿日期：2022-04-19

作者簡介：唐友亮（1977—），男，山東臨沂人，碩士研究生，教授，主要從事數字化設計與制造技術、機電一體化控制技術方面的教學與研究工作。