四輪轉向汽車的無模型自適應控制研究

許佳東 高遠 袁海英

摘? ?要：為提高四輪轉向汽車的操縱穩定性，提出一種以質心側偏角和橫擺角速度為反饋量，以后輪轉角與橫擺力矩為控制器輸出的四輪轉向汽車無模型自適應控制方法。具體設計方案為：從建立等效車輛的雙輸入-雙輸出緊格式線性化模型出發，結合車輛轉向動力學的理想模型，引入輸入準則函數和參數估計準則函數，采用極值原理分別設計出無模型自適應控制器及其偽雅可比矩陣的估計律，并理論分析了該控制方法的系統穩定性。該方法的控制器設計不依賴精確的整車數學模型，且具有后輪轉角與橫擺力矩相結合的復合控制特點。控制仿真對比結果表明：在不同車速和轉向工況下，該控制方法均能對期望的橫擺角速度與質心側偏角具有良好的跟蹤效果，有效提高了四輪轉向汽車低速轉向的機動靈活性和高速行駛轉向的操縱穩定性。

關鍵詞：四輪轉向汽車;無模型自適應控制方法;動力學數學模型

中圖分類號：TP273.2? ? ? ? ? ? ? DOI：10.16375/j.cnki.cn45-1395/t.2022.03.005

0? ? 引言

四輪轉向（four-wheel steering，4WS）汽車技術作為主動底盤控制系統的一種重要組成，已成為提高現代汽車主動安全性的發展趨勢和新興技術之一，倍受人們關注[1]。控制策略是4WS技術研究的重要方面，也是實現4WS車輛獲得低速轉向機動靈活性和高速行駛轉向操縱穩定性的重要保證[2]。

迄今，針對4WS系統的控制問題，研究者們提出了前后輪轉角成比例的前饋控制[3]、滑模控制[4]、模糊控制[5]等主動后輪轉向控制方法，在一定程度上能改善車輛高速行駛的操縱穩定性和低速狀態的機動靈活性。鑒于直接橫擺力矩控制（direct yaw-moment control，DYC）作為當前另一種有效的汽車底盤控制技術，從提高4WS車輛動力學行駛穩定性角度考慮，提出了最優控制[6]、自適應滑模控制[7]、非光滑控制[8]等橫擺力矩控制策略。然而，這些不同的單一控制方法，大都采用忽略輪胎與地面間非線性作用、低自由度的汽車轉向數學模型[9]，故在改善汽車操縱穩定性方面的作用有限，特別是在車輛高速、急轉彎等極限工況下，難以獲得滿意的控制性能，甚至會出現穩定性惡化現象。近年來，有學者提出神經網絡[10]、遺傳算法[11]等智能控制方法，以降低方法對轉向數學模型的依賴性，但存在在線運算難以滿足實時性控制的要求。近幾年，研究者們提出了后輪主動轉向控制技術和橫擺力矩控制技術相結合的聯合（或復合）控制方法[12]，可獲得比單一控制方法更優的控制性能，能進一步改善車輛的操縱穩定性。

為提高4WS汽車低速轉向的機動靈活性和高速行駛轉向的操縱穩定性，本文提出了一種車輛后輪轉角與橫擺力矩相結合、具有復合控制特點的無模型自適應控制（model-free adaptive control，MFAC）方法，設計出雙輸入-雙輸出的無模型自適應控制器，并進行4WS控制系統的穩定性證明。搭建七自由度4WS車輛動力學仿真模型，不同控制方法的仿真對比結果驗證了本文所提方法的有 效性。

1? ? 4WS汽車的動力學數學模型

1.1? ?七自由度的轉向整車數學模型

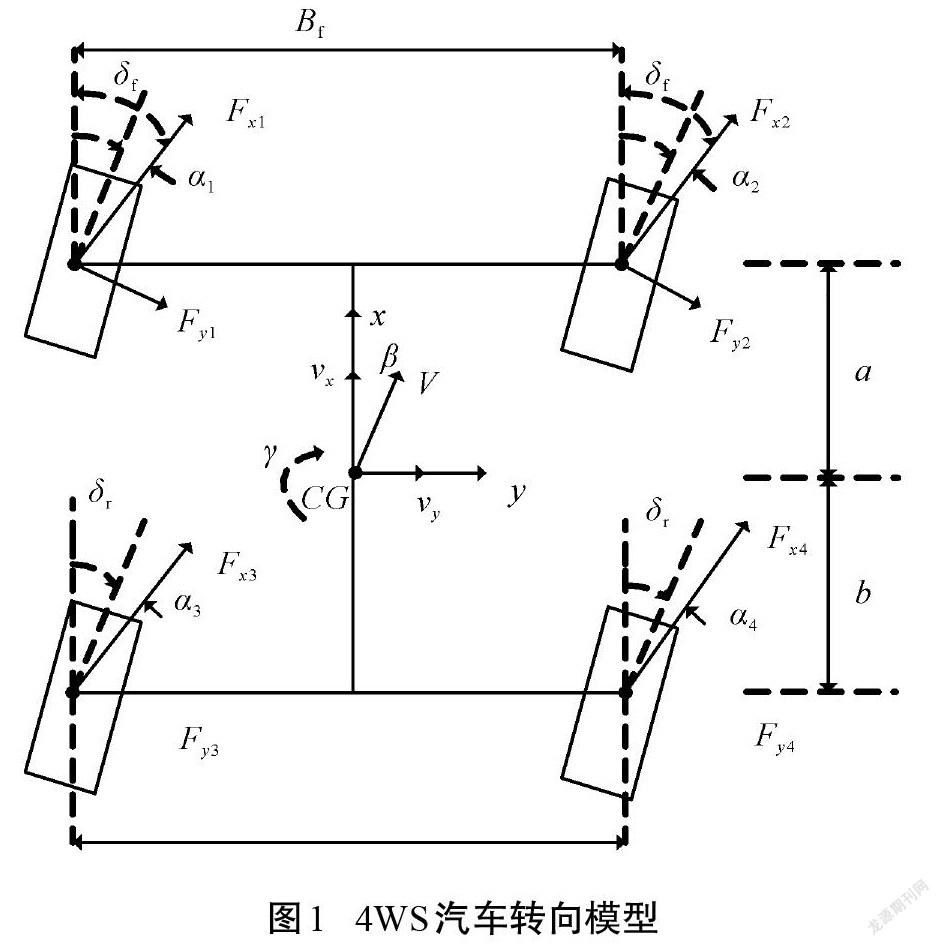
圖1為七自由度的車輛轉向運動學模型圖。圖中，[Fxi]、[Fyi]分別表示輪胎所受的縱向力和橫向力（下標[i=1， 2， 3， 4]分別表示左前輪、右前輪、左后輪和右后輪）;[δf]、[δr]分別為4WS汽車的前、后輪轉向角;[a]、[b]分別為汽車質心到前軸、后軸的距離，L= [a] + [b]即是車的軸距;[Bf] =[Br] =[W]為輪距;[vx]、[vy]分別表示汽車質心速度[V]在[x]和[y]軸上的速度分量;[γ]是汽車橫擺角速度;[ωi]為各輪胎的轉動角速度。該模型圖給出了汽車繞[x]軸的縱向運動、繞[y]軸的橫向運動、繞[z]軸的橫擺運動，以及汽車4個輪胎的運動情況[13]。

根據汽車動力學理論，可建立起如下七自由度的4WS整車數學模型：

[m（vx-vyγ）=（Fx1+Fx2）cosδf-（Fy1+Fy2）cosδr+? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（Fx3+Fx4）sinδf-（Fy3+Fy4）sinδr，m（vy+vxγ）=（Fx1+Fx2）sinδf+（Fy1+Fy2）cosδf+? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（Fx3+Fx4）sinδr+（Fy3+Fy4）sinδr，Izγ=a[（Fy1+Fy2）cosδf]-b[（Fy3+Fy4）cosδr]+? ? ? ? ? 0.5W[（Fy1-Fy2）sinδf+（Fy3-Fy4）cosδr]+M，Jwωi=Mdi-FxiR-Mbi， i=1， 2， 3， 4.]（1）

式中：[m]為整車質量，[Iz]為汽車繞z軸的轉動慣量，[Jwωi]為各輪胎的轉動慣量，R為輪胎半徑，[Mdi]為差速器半軸上的輸出扭矩，[Mbi]為輪胎所受的制動力矩，[M]表示車輪所受縱向力對車身所產生的附加橫擺力矩，其值為：

[M=a（Fx1+Fx2）sinδf-b（Fx3+Fx4）sinδr+]? ? ? ? [0.5W[（Fx2-Fx1）cosδf+（Fx4-Fx3）cosδr]].? ? （2）

結合圖1，根據汽車沿[x]軸和[y]軸上的速度分量可求出車輛質心側偏角[β]：

[β=arctan（vx/vy）] .? ? ? ? ? ? ? ? ? ? （3）

式（1）中的汽車運動縱向力和橫向力可利用現有的車輛輪胎數學模型予以表達。本文采用文獻[14]的Gim輪胎模型來體現車輛輪胎與地面間的非線性作用力特性，以及反映縱向力和橫向側偏力與剛度、路面附著系數的定量數學關系。

1.2? ?理想的車輛動力學模型

4WS汽車的控制，其本質是控制車輛運動狀態，實現對理想目標狀態的跟蹤。假定汽車處于小角度轉向的[vx]≈V正常時速行駛工況，此時只考慮車輛側滑和橫擺運動，那么可選擇質心側偏角[β]和橫擺角速度[γ]作為衡量操縱穩定性的主要指標。在汽車正常運行且不改變駕駛員駕駛習慣的情況下，為提高汽車低速轉向過程的機動靈活性和高速轉向過程的操縱穩定性，可將具有穩態的期望橫擺角速度[γd]作為4WS車輛[γ]的控制目標。為使車輛轉彎過程保持良好的車身姿態，要求[β]能趨于0或其附近的期望質心側偏角[βd]。

考慮[γ]對前輪轉角輸入[δf]的響應瞬態延遲，引入如下的一階滯后環節，表明[γd]也具有該延遲效應[15]：

[γd（s）=kγ11+τγsδf（s）].? ? ? ? ? ? ? ?（4）

其中：[kγ]是[γd]相對前輪轉角的一階滯后響應的增益系數，[τγ]表示一階滯后環節的滯后時間常數，兩者的數學表達式分別為[kγ=Va+mabV2/2Cfa（a+b）]、[τγ=IzV2Cfa（a+b）+mbV2]，[Cf]為汽車前輪側偏角? ?剛度。

定義期望狀態矢量[xd=βdγdT]和期望輸出矢量[yd]，可建立起如下的車輛轉向理想模型：

[xd=Adxd+Bdδf，yd=xd.]? ? ? ? ? ? ? ? ? ? ? ? ? （5）

式中： [A=diag0-1τγ]，[Bd=0kγτγT]。

2? ? 4WS汽車的無模型自適應控制方法

鑒于單一的后輪轉角主動控制策略在改善4WS車輛轉向機動靈活性和操縱穩定性方面效果有限，橫擺力矩控制也是提高車身動力學穩定性的一種有效策略。為降低控制器設計對精確對象或系統數學模型的依賴性，提高不同行駛工況下的控制性能，本文提出一種如圖2所示的4WS車輛MFAC方法。由圖2可見，控制系統以4WS汽車的質心側偏角和橫擺角速度為反饋量，將質心側偏角控制誤差[eβ]和橫擺角速度控制誤差[eγ]作為MFAC控制器輸入，控制器輸出后輪轉角與橫擺力矩以聯合控制4WS車輛。

2.1? ?多輸入、多輸出的4WS動態線性化過程

根據圖2所示的4WS汽車控制系統原理，可將4WS車輛模型等價為如下的雙輸入-雙輸出的非線性離散時間系統[16]：

[y（k+1）=f（u（k）， u（k-1）， …， u（k-ni），]

[ y（k）， y（k-1）， …， y（k-no））].? ? ?（6）

式中：[u（k）=δr（k）M（k）T∈R2×1]為4WS車輛控制輸入矢量;[y（k）=β（k）γ（k）T∈R2×1]為車輛姿態輸出矢量;[f（k）∈R2×1]為未知的非線性函數向量;[ni、no∈Z]（[Z]為整數集）為2個整數，分別表示輸入、輸出信號序列的長度。鑒于方向盤的操作使得前輪轉角連續性變化，同時從汽車動力學安全穩定性角度考慮，后輪轉角和橫擺力矩的控制作用也應非跳變，且滿足有界輸入和有界輸出（BIBO）的穩定性要求。因此，引入如下的2個假設條件：

假設1? ?函數[f（·）]關于控制輸入[u（k）]的偏導數是連續的。

假設2? 該系統滿足Lipschitz條件，即對任意的[k]和[Δu（k）≠0]，存在關系：

[Δy（k+1）≤ξΔu（k）] .? ? ? ? ? ? ? ?（7）

式中：[Δy（k+1）=y（k+1）-y（k）]，[Δu（k）=u（k）-u（k-1）]，且[ξ]為大于0的常數，[·]表示2范數。

引理1? 對于滿足上述假設條件的非線性離散時間系統（6），對任意的[k]和[Δu（k）≠0]，必然存在一個偽雅可比矩陣[φ（k）]，使得系統（6）可轉化為以下形式的緊格式動態線性化數學模型：

[Δy（k+1）=φ（k）?Δu（k）] .? ? ? ? ? ? ? （8）

式中：[φ（k）=φ11φ21? ?φ12φ22∈R2×2]，且滿足[φ（k）≤ξ]。

引理1 的證明見參考文獻[17]。偽雅可比矩陣[φ（k）]反映了雙輸入與雙輸出之間的耦合關系，矩陣各元素的數值大小表示耦合作用的緊密性，且數值的有界性滿足BIBO條件要求。為充分發揮[δr（k）]、[M（k）]分別在提高轉向運動軌跡跟蹤能力和車身動力學穩定性方面的控制優勢作用，對[φ（k）]的元素數值引入權重假設。

假設3? 偽雅可比矩陣[φ（k）]滿足對角占優條件，即滿足關系：

[φij（k）i≠j≤ξ1]，[ξ2≤φij（k）i=j≤αξ2] .? ? ? ? （9）

式中：[α≥1];[i=1， 2];[j=1， 2];[ξ2≥ξ1（2α+1）]，[ξ1] 、[ξ2]表示2個大于0的常數。

2.2? ?控制算法設計

為使4WS汽車滿足不同車速轉向情況對機動靈活性和操縱穩定性的要求，設計恰當的控制律[u（k）]，控制車輛姿態[y（k）]對期望目標[yd（k）]的平穩趨近跟蹤。為體現車輛姿態的跟蹤控制性能和控制作用的平穩性，引入如下的準則函數：

[Ju（k）=yd（k+1）-y（k+1）2+]

[λu（k）-u（k-1）2] .? ? ? ? ? ? ? ? （10）

式中：權重因子[λ>0]，反映限制輸入量過大變化的重視程度。基于準則函數最小值準則，將式（8）代入式（10），并對[u（k）]進行極值運算，則可得到：

[u（k）=u（k-1）+ρφT（k）（yd（k+1）-y（k））λ+φ（k）2].（11）

式中：[ρ∈0， 1]是步長因子。由于式（6）非線性函數未知，難以得到式（11）中準確的偽雅可比矩陣。因此，本文采用最小參數估計準則函數思想來設計偽雅可比矩陣的估計算法。首先定義如下形式的估計準則函數：

[Jφ（k）=Δy（k+1）-φ（k）Δu（k+1）2+]

[ζφ（k）-φ（k-1）2] .? ? ? ? ? ? ? ? ? ? ? （12）

式中：[ζ>0]是權重因子。對上式估計準則函數進行極值運算，可獲得[φ（k）]的估計算法：

[φ（k）=]

[η（Δy（k+1）-φ（k-1）Δu（k-1））?ΔuT（k-1）ζ+Δu（k）2+φ（k-1）] .? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（13）

式中：[η∈0， 2]是步長因子。通過對[φ（k）]的估計，所設計的無模型自適應控制器表達式（11）變為：

[u（k）=u（k-1）+ρφT（k）（yd（k+1）-y（k））λ+φ（k）2]. （14）

為保證偽雅可比矩陣在合理的范圍內變化，偽雅可比矩陣的估計算法中引入一種重置機制，即當[φ（k）≤ε]或[sgn（φ（k））≠sgn（φ（1））]時，有[φ（k）=φ（1）]，其中[ε]是一個很小的正數。

2.3? ?控制系統穩定性分析

定義控制誤差向量[e=yd（k）-y（k）]。現結合緊格式動態線性化系統模型式（8），證明在估計算法（13）和控制律（14）的作用下，通過對[φ（k）]的有界估計，使得4WS車輛的控制誤差向量滿足[limk→∞e=0]。

證明如下：

定義偽雅可比矩陣估計的誤差矩陣[φ（k）=φ（k）-φ（k）]，則式（13）變為：

[φ（k）=φ（k-1）+φ（k-1）-φ（k）-]

[ηφ（k-1）Δu（k-1）?ΔuT（k-1）ζ+Δu（k）2].? ? ? （15）

由引理1可知，由于[φ（k）≤ξ]，所以[φ（k-1）-φ（k）≤2ξ]。令[z=ηΔu（k-1）2ζ+Δu（k-1）2]，由于[η∈0， 2]，且[ζ>0]，那么有：

[0≤z<2].? ? ? ? ? ? ? ? ? ? ? （16）

對式（15）兩邊取范數，利用[z]的定義式進行簡化有：

[φ（k）≤2ξ+φ（k-1）-]

[ηφ（k-1）Δu（k-1）?ΔuT（k-1）ζ+Δu（k-1）2=]

[2ξ+φ（k-1）-φ（k-1）z] .? ? ? ? （17）

并對式（17）最后兩項取平方得：

[z-2z+1?φ（k-1）2≥0] .? ? ? ?（18）

結合式（18）和式（16）可知，[z]的邊界關系為：

[1≤z<2] .? ? ? ? ? ? ? ? ? ? ? ? （19）

所以可存在一個[d=（1-z）∈-1， 0]，使得：

[φ（k）≤2ξ+dφ（k-1）≤]

[1-dk-11-d2ξ+dk-1φ（1）] .? ? ? ? ? ? （20）

由式（20）可知，[φ（k）]有界，這表明對偽雅可比矩陣的估計[φ（k）]也是有界的。

當[k→∞]時，轉向理想模型的輸出[yd（k）]具有穩態特性，即有[yd（k+1）=yd（k）]。聯立式（8）和式（14）可得：

[Δy（k+1）=ρφ（k）φT（k）λ+φ（k）2（yd（k+1）-y（k）），y（k+1）-y（k）=ρφ（k）φT（k）λ+φ（k）2（yd（k+1）-y（k）），e（k）-e（k+1）=ρφ（k）φT（k）λ+φ（k）2e（k），e（k+1）=1-ρφ（k）φT（k）λ+φ（k）2?e（k） .]

（21）

由于[ρ∈0， 1]，且[λ>0]，則：

[1-ρφ（k）φT（k）λ+φ（k）2∈0， 1].? ? ? ? ? ? ? （22）

根據式（21）和式（22），故有[limk→∞e（k）=0]。

3? ? 仿真分析

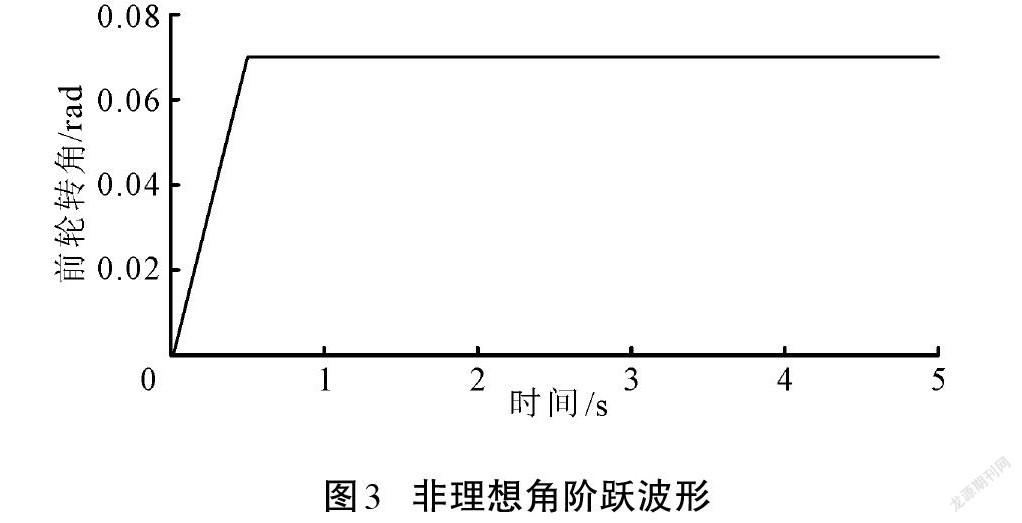
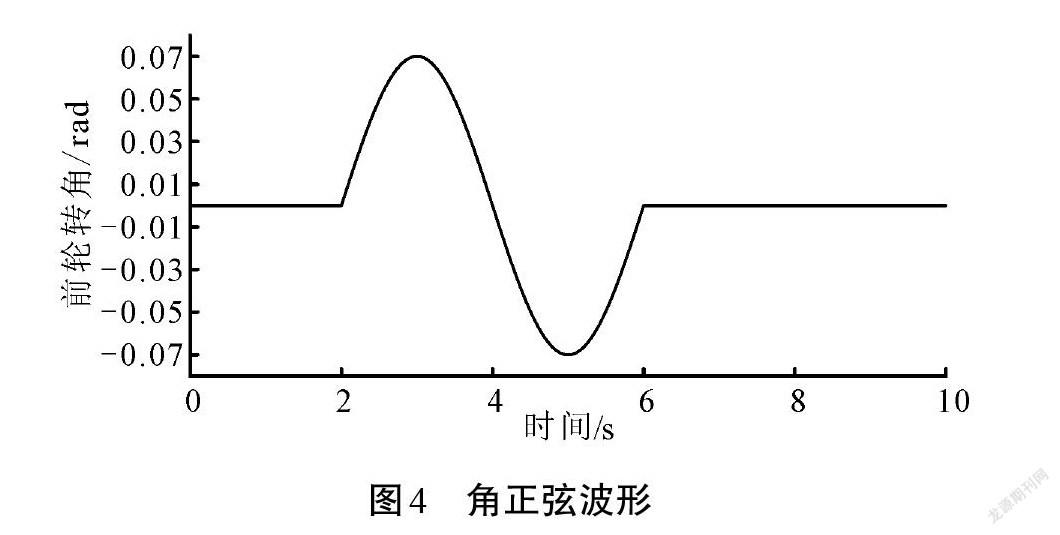
結合圖2所示的系統框圖，利用Matlab/Simulink軟件環境將七自由度整車模型式（1）、文獻[14]輪胎模型、轉向理想模型式（5）、偽雅可比矩陣估計律式（13）、控制器表達式（14）等模塊程序化，建立起4WS汽車控制仿真模型。對模型設置表1車輛參數，設置控制器及估計律有關參數[ρ=η=ζ=1]、[λ=1.5]、[ε=10-5]、[φ（1）=diag2-0.1]。為驗證MFAC控制方法的有效性，控制仿真一方面考慮不同車速（20 km/h和100 km/h），以及前輪不同波形（圖3的非理想角階躍波形和圖4的角正弦波形）轉向的行駛工況;另一方面對比無控制的前輪轉向（FWS）汽車（簡記：無控制）、文獻[3]的后輪轉角比例前饋控制4WS汽車（簡記：比例前饋）的轉向性能效果。

圖5給出了4WS汽車不同行駛工況下的質心側偏角控制響應曲線。比較圖5（a）—圖5（d）可知，無控制的FWS汽車，各種行駛工況下的質心側偏角穩態響應均不為0，特別是高速轉彎時，質心側偏角數值較大且與前輪轉角方向相反，這反映出高速行駛的FWS汽車甩尾和側滑的趨勢增大。當4WS汽車實施MFAC控制，相比后輪轉角比例前饋控制方法，不同行駛工況均能實現質心側偏角為0，達到理想的期望穩定狀態，使得4WS汽車能很好地維持車身姿態，具有良好的路徑跟蹤能力，極大地改善了汽車的操縱性。

圖6給出了4WS汽車在不同行駛工況下的橫擺角速度控制響應曲線。由圖6可以看出，無控制的FWS汽車，高速車輛階躍波形轉向時的橫擺角速度響應具有較大的超調振蕩現象，易發生嚴重的激轉現象，從而使車輛失去穩定性。4WS汽車受MFAC控制時，相比單一的后輪轉角比例前饋控制，能獲得更優的橫擺角速度期望跟蹤控制性能。低速時[γ]較大，有助于汽車低速轉向時少打方向盤或減少轉彎半徑，進而提高車輛低速轉彎的機動靈活性;高速時[γ]較小，不存在前饋控制的超調現象，且振蕩現象明顯得到抑制，特別是階躍波形轉向情形，無超調和振動現象，這表明4WS汽車的行駛穩定性得到有效提高，降低汽車高速狀態下駕駛員猛打方向盤造成的危險。

4? ? 結論

本文所提出的4WS汽車無模型自適應控制方法，其控制器設計基于系統輸入和輸出信號構建的緊格式動態模型，不依賴4WS系統精確的數學模型及參數;其根據緊格式動態線性化模型和車輛理想轉向模型，引入輸入準則函數和參數估計準則函數，并利用極值原理設計出無模型自適應控制器，是一種后輪轉角控制和直接橫擺力矩控制相結合的復合控制方法。仿真結果表明，在不同的車速和轉向條件下，該控制方法以車輛轉向理想模型輸出作為控制期望，相比于后輪轉角的比例前饋控制方法，能較好地對質心側偏角和橫擺角速度進行穩定跟蹤控制，并有效地提高了汽車的行駛操縱穩定性和安全性。

參考文獻

[1]? ? ?胡紅元，李兵，王陽陽.汽車四輪轉向技術研究綜述[J].上海汽車，2021（4）：19-23.

[2]? ? ?姬曉，李剛，曹天琳.四輪獨立驅動與轉向電動汽車四輪轉向研究綜述[J].汽車實用技術，2020，45（17）：5-7.

[3]? ? ?SANO S， FURUKAWA Y， SHIRAISHI S. Four wheel steering system with rear wheel steer angle controlled as a function of steering wheel angle[C]// International Congress and Exposition，February 24，1986. SAE Technical Paper 860625，1986. DOI：10.4271/860625.

[4]? ? ?TAN L，YU S Y，GUO Y，et al. Sliding-mode control of four wheel steering systems[C]//2017 IEEE International Conference on Mechatro-nics and Automation，ICMA 2017. IEEE，2017：1250-1255.

[5]? ? ?CHEN L，LI? P? S， LIN? W? S， et al. Observer-based fuzzy control for four-wheel independently driven electric vehicles with active steering systems[J]. International Journal of Fuzzy Systems，2020，22（1）：89-100.

[6]? ? ?姚世鵬，熊歡，蘭曉霞，等.汽車四輪轉向最優控制技術的研究[J].船電技術，2018，38（11）：33-36，42.

[7]? ? ?ASIABAR A N，KAZEMI R. A direct yaw moment? controller for a four in-wheel motor drive electric vehicle using adaptive sliding mode control[J]. Proceedings of the Institution of Mechanical Engineers，Part K：Journal of? Multi-body Dynamics，2019，233（3）：549-567.

[8]? ? ?葉慧，李國政，丁世宏，等.基于非光滑控制技術的電動汽車直接橫擺力矩控制[J].江蘇大學學報（自然科學版），2018，39（6）：640-646.

[9]? ? ?嚴帥，張緩緩，高超，等.基于Simulink仿真的線性三自由度汽車操縱模型[J].智能計算機與應用，2020，10（2）：200-203，207.

[10]? ?王雪嬌.基于BP神經網絡的四輪轉向汽車操縱穩定性仿真[J].荊楚理工學院學報，2017，32（2）：45-50.

[11]? ?羅玉濤，周天陽，許曉通.基于遺傳算法的四輪轉向-驅動汽車時變LQR控制[J].華南理工大學學報（自然科學版），2021，49（3）：114-122.

[12]? ?徐坤，王云超，沈建. 四輪獨立驅動電動汽車四輪轉向和橫擺力矩聯合控制仿真[J].集美大學學報（自然科學版），2018，23（2）：139-144.

[13]? ?王振剛，范健文，高遠，等.四輪轉向車輛操縱穩定性的最優控制策略研究[J].廣西科技大學學報，2015，26（1）：1-6，17.

[14]? ?屈求真，劉延柱. 汽車輪胎側偏特性的研究現狀及其發展[J]. 上海交通大學學報，1999，33（6）：755-759.

[15]? ?NAGAI M， SHINO M， GAO F . Study on integrated control of active front steer angle and direct yaw moment[J]. Review of Automotive Engineering，2002，23（3）：309-315.

[16]? ?王洪斌，左佳鑠，劉世達，等.無人駕駛車輛穩態漂移的無模型自適應控制[J].控制理論與應用，2021，38（1）：23-32.

[17]? ?HOU Z，JIN S. Data-driven model-free adaptive control for a class of mimo nonlinear discrete-time systems[J]. IEEE Transactions on Neural Networks，2011，22（12）：2173-2188.

The model-free adaptive control of

four-wheel steering vehicle

XU Jiadong1 ， GAO Yuan*1，2 ， YUAN Haiying1

（1.School of? Electrical， Electronic and Computer Science， Guangxi University of Science and

Technology， Liuzhou 545616， China; 2. Guangxi Key Laboratory of Automobile Components and Vehicle

Technology（Guangxi University of? Science and Technology）， Liuzhou 545006， China）

Abstract： A model-free adaptive control （MFAC） strategy was presented to improve the steering stability of four-wheel steering （4WS） vehicle， which took side slip angle and yaw rate as feedback， and the rear wheel angle and yaw moment as the controller output. The design scheme was as follows： firstly， the double-input-double-output compact linearization model of the equivalent vehicle was established combined with the ideal model of vehicle steering dynamics; secondly， the input criterion function and parameter estimation criterion function were introduced; thirdly， MFAC controller and the estimation law of pseudo Jacobian matrix were designed respectively by the extremum principle;? finally， the stability of the 4WS control system was analyzed. The proposed method provides a compound controller with the combination of rear steer angle and direct yaw moment， where the design process is independent of the accurate 4WS model. The control simulation results of 4WS vehicle show that under different vehicle speeds and steering conditions， the control method can track the expected yaw rate and side slip angle， and effectively improves the maneuverability of low-speed steering and the steering stability of high-speed steering of 4WS vehicle.

Key words： four-wheel steering vehicle; model-free adaptive control; dynamic mathematic model

（責任編輯：羅小芬）