球形貯箱內液體橫向晃動問題的系統辨識與參數化等效建模

王佐 吳文軍 姜丙超 高超南

摘? 要：為解決傳統等效力學模型描述貯箱內液體晃動特性時在準確性和完整性等方面存在不足的問題，首先，運用勢流理論推導出部分充液圓柱貯箱的動力學狀態方程，依據方程中液體晃動速度勢函數與晃動波高函數中傅里葉-貝塞爾級數展開系數的正交性條件，將球形貯箱內液體晃動的求解區域向與之外切的圓柱貯箱求解區域內進行擴展，建立用于描述球形貯箱內液體晃動問題的參數化模型;然后，通過CFD數值模擬實驗得到球形貯箱受橫向簡諧激勵時小幅晃動情況下的液體晃動力和力矩;最后，利用Matlab灰箱辨識函數對所建立的參數化模型中的待定系數進行準確辨識，實現了球形貯箱內液體橫向晃動問題的高精度等效建模。結果表明：所建立的參數化等效力學模型能較準確和完整地描述球形貯箱內的液體晃動固有頻率、晃動力和晃動力矩等動力學特性，辨識精度均能達到92%以上，為進一步在線實時辨識與實際工程應用提供參考。

關鍵詞：球形貯箱;液體晃動;參數化模型;CFD數值模擬;灰箱辨識;系統辨識

中圖分類號：O353.1? ? ? ? ?DOI：10.16375/j.cnki.cn45-1395/t.2022.03.001

0? ? 引言

液體晃動現象普遍存在于人們的生活與生產中，液體晃動導致的安全和穩定性問題長期影響著各充液系統應用行業技術的發展。對于受外部干擾作用的貯箱內液體晃動產生的動態非平衡晃動力和晃動力矩的研究，在交通運輸[1-4]、液體能源儲存[5-6]和航空航天[7-13]等工程領域受到學者們的普遍關注。

建立液體晃動系統的力學模型是研究液體晃動特性的重要手段。傳統單擺模型研究中，包光偉[14]針對平放式貯箱內的液體晃動特性建立單擺模型來對其進行描述;苗楠等[15]對單擺模型各個參數插值建立航天液體燃料晃動模型，并進行了變充液比工況下的輸出響應仿真驗證。質量-彈簧模型研究中，劉嘉一等[16]利用建立的三維質量-彈簧模型計算了水平載荷時的液體作用力;岳寶增等[17]在解析帶柔性附件充液航天器耦合特性時將液體晃動等效為球擺模型。此類傳統等效力學模型具有計算量小和效率高的優點，但是簡化假設較多，制約了傳統力學模型描述液體高階晃動模態時的完整性，且可控、可調參數的數目較少，使其準確性也受到了限制。近年來涌現出的各類新型模型有復合模型[18]、運動脈動球模型（moving pulsating ball model，MPBM）[19]、深度學習預測模型[20]、幅度組合模型[21]和參數化模型[22-23]，以上模型對液體晃動系統的特性表達精度較傳統等效力學模型有了較大提高，其中參數化模型不僅可控、可變參數多，而且描述高階晃動模態時精準度高。文獻[22-23]中的參數化模型均是在傳統等效單擺模型的基礎上對模型進行參數確定方法的優化，盡管比傳統等效模型有所提升，但受限于傳統力學模型框架結構單一的特點而無法對液體復雜工況下的晃動行為進行描述。動力學系統建模需對研究對象進行系統辨識和參數估計，測量實驗和CFD模擬實驗均可獲得系統的輸入、輸出響應，但實驗測量法[24-26]往往存在實驗誤差，且相似比選取不恰當時模擬實際工況程度較低或成本高，而CFD數值模擬方法[27-30]成本低、適用性強和準確性高，且對液體晃動系統進行激勵輸入時準確無延遲。

結合以上研究現狀，本研究擬通過勢流理論推導出部分充液圓柱貯箱液體晃動的線性化狀態空間表達式，將其擴展應用到充液球形貯箱內液體晃動的動力學系統，利用CFD數值模擬對充液球形貯箱進行自振特性和不同頻率下的同系統晃動模擬仿真實驗，并在Matlab中利用線性灰度模型（linear grey-box models）進行參數估計，以期建立高精準度的充液球形貯箱內液體晃動的參數化模型。

1? ? 液體晃動的動力學模型

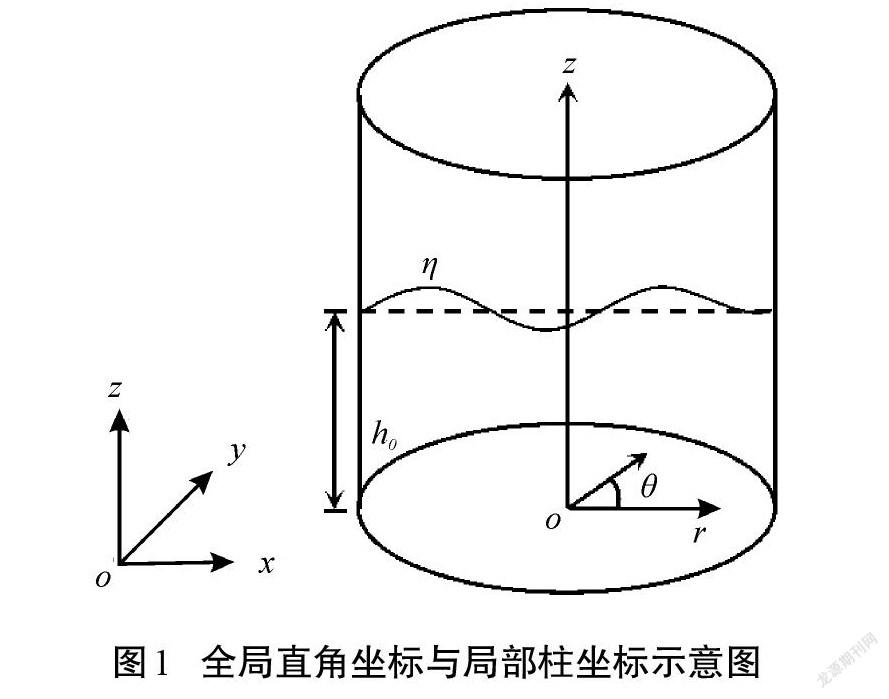
假設圓柱貯箱內的液體為理想流體，貯箱壁面為剛體，模態坐標如圖1所示。

圖1中全局坐標為直角坐標系[o-xyz]，局部柱坐標[o-rθz]，以貯箱底部圓心為坐標原點，隨貯箱的移動而移動，[h0]為初始液面與貯箱底部的高度差，[η（r， θ， t）]為液面波高函數。根據文獻[31]中的勢流理論，且不考慮環向晃動模態，當貯箱重力加速度受到[xt]的橫向水平激勵作用時，液體相對壁面的速度勢函數和貯箱對液體的牽連速度勢函數簡化為：

[?rr， θ， z， t=n=1∞ant（cosθ）J1λnrR0coshλnzcoshλnh0]，? （1）[?e=v（t）rcosθ]. （2）

式中：[?]為液體晃動速度勢函數，分為2個部分，相對速度勢函數[?r]和牽連速度勢函數[?e];[r]為徑向坐標，取值范圍是[0<r<R0];[J1]為一階Bessel函數;[λn]為方程[J1′（λn）=0]的正根;[ant]是關于時間的任意函數;[R0]為柱體半徑;[v（t）]是貯箱的橫向運動速度。

波高函數為：

[ηr， θ， t=-n=1∞bnt（cosθ）J1λnrR0]? .? （3）

式中：[bnt]是關于時間的任意函數。

將式（1）和式（3）代入如下的自由液面處動力學等壓條件和運動學等速邊界條件，可得：

[???t+gηSt=0] ，? ? ? ? ? ? ? ? ? ? ?（4）

[?η?t+???zSt=0] .? ? ? ? ? ? ? ? ? ? ?（5）

式中：[g]為垂直于理想靜止液面向下的重力加速度。為得到動力學控制方程，利用傅里葉-貝塞爾函數展開系數的正交性，綜合考慮小幅晃動情況下液體晃動的一階反對稱模態占優[32]，經過代數運算，最終可將系統的狀態方程轉換為如下一階微分狀態方程：

[ddtb1ta1（t）=01-ω2-2ωζb1（t）a1（t）+0Aax（t）].? （6）

式中：[ω]為貯箱內液體周期晃動的一階圓頻率，[ζ]為阻尼比，[A]為輸入矩陣系數。

系統輸出方程為：

[FxMy=B11B12B21B22b1（t）a1（t）+C1C2ax（t）].? ? ? （7）

式中：[Fx]為x軸方向上液體對貯箱壁面的橫向晃動力;[My]為y軸方向上液體對貯箱整體的晃動力矩;[B11]、[B12]、[B21]、[B22]、[C1]、[C2]均為輸出矩陣系數;[ax（t）]為隨時間變化的橫向加速度激勵。液體壓強在貯箱內壁面上進行積分即可算得晃動力和晃動力矩，結合勢函數和波高函數展開系數來對狀態向量進行唯一確定，式（6）和式（7）構成圓柱貯箱內液體小幅晃動的線性參數化模型。在充液圓柱貯箱液體晃動建模的推導中，液體晃動的速度勢函數和波高函數的傅里葉-貝塞爾級數展開系數可以構成一個完備的正交系，球形貯箱空間內切于此正交系所在空間，如圖2所示。

當球形貯箱內液體小幅晃動時，其內部不產生氣泡，自由液面也不出現破碎的現象，則可假設液體晃動的速度勢函數和自由液面處的波高函數均滿足連續無間斷點條件。利用傅里葉-貝塞爾級數展開法，可將未知的球形貯箱液體晃動速度勢函數和波高函數在與球形貯箱外切的圓柱貯箱區域內進行級數展開，最終也可以分別建立類似于式（6）的動力學狀態方程和式（7）系統輸出方程的線性參數化模型，從而實現球形貯箱內液體晃動問題的參數化建模。實際上，雖然傳統的等效單擺模型與質量彈簧阻尼模型的最終動力學狀態方程也具有和式（6）、式（7）相似的動力學狀態方程和系統輸出方程，但由于前者存在幾何物理性質的限制，相應的方程形式也受到約束，實際應用中并不能實現液體晃動動態特性的完整描述。而本文提出的參數化模型卻不存在該類限制，將更具有靈活性和適應性，可依據實際的晃動特性進行合理的修訂和優化。這一點在有限幅非線性晃動問題上具有明顯的優勢，可參照非線性度相關性分析結果，對模型的輸入、輸出形式進行相應調整后建立適當的模型。

2? ? 液體晃動數值模擬實驗

利用CFD數值仿真軟件對部分充液球形貯箱內液體小幅晃動進行模擬，設定球形貯箱的內徑為300 mm，壁厚4 mm，罐內壁面彈性屬性為剛體，貯箱內液體為水且體積占球形貯箱體積的一半，重力加速度與圖1全局直角坐標系中[z]方向相反且大小為9.8 m/s2。

2.1? ?自振特性實驗

工程上常用瞬態激振法進行自振特性實驗，其原理是當穩定的系統結構受到瞬態激勵后不再繼續受到任何外力時，系統會以某一頻率進行周期振動，此頻率為系統的自振頻率（固有頻率）。

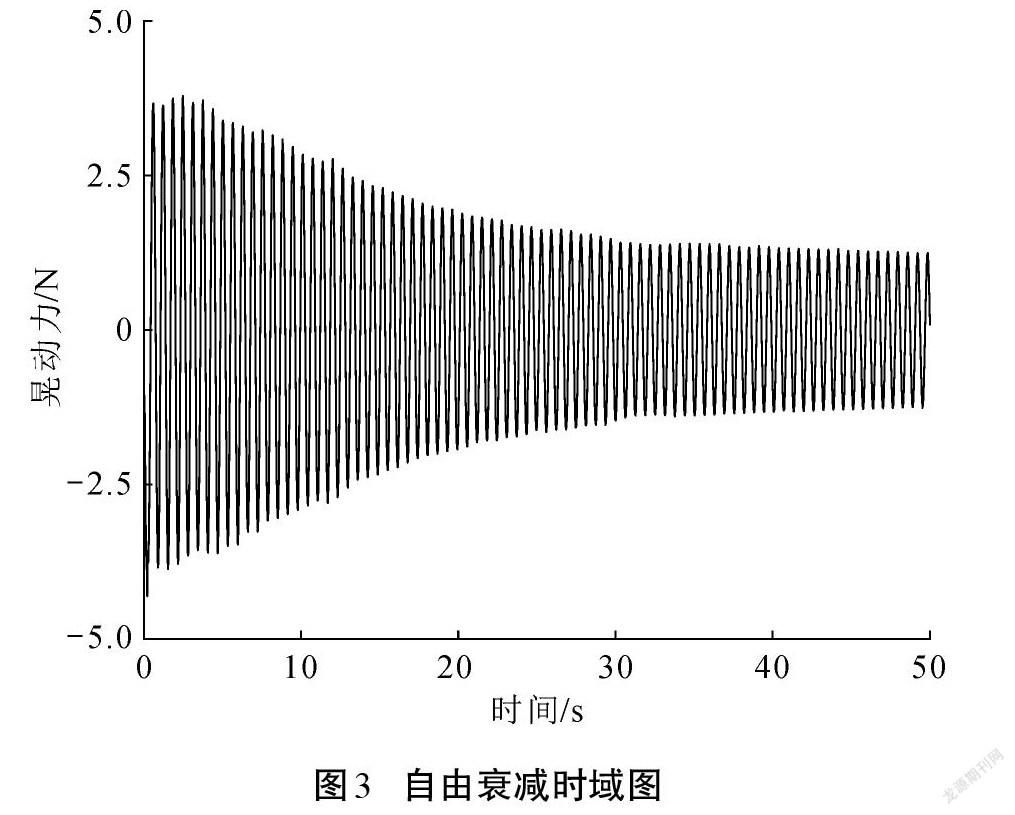
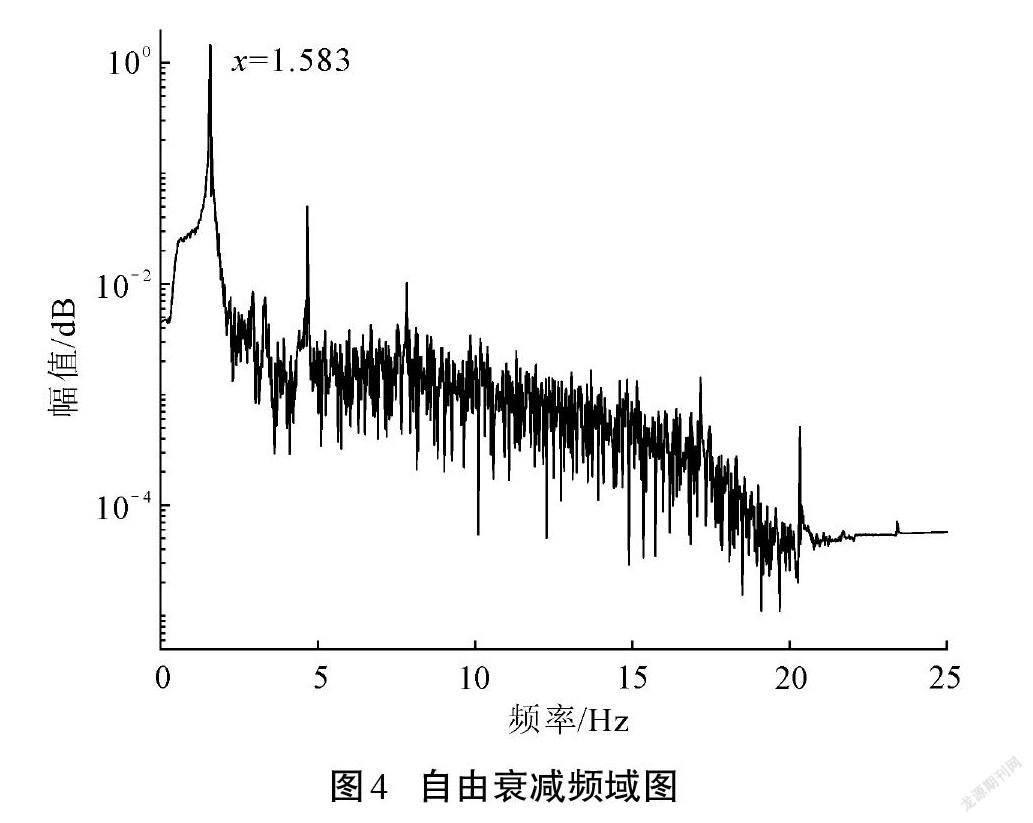
為后續建立液體晃動的動力學系統模型時對初始頻率進行精準設定，尋找系統一階固有頻率十分必要。本次采用瞬態激振法對充液球形貯箱內液體晃動系統進行自振特性實驗研究。在數值模擬實驗中，設定外部激勵為單次短時橫向加速度激勵，加速度幅值使液體晃動幅度在小幅晃動范圍內;然后采集液體對貯箱壁面的晃動力信號和液體晃動對貯箱整體的晃動力矩信號，并對其進行傅里葉變換。晃動力和晃動力矩性質相似，僅以晃動力為例繪制晃動力信號自由變減時域圖與頻域圖如圖3、圖4所示。結果表明，半充液球形貯箱內液體小幅晃動系統的一階固有頻率約為1.58 Hz，以此作為參數化等效灰度模型系統辨識時的初始頻率值。

2.2? ?強迫晃動實驗

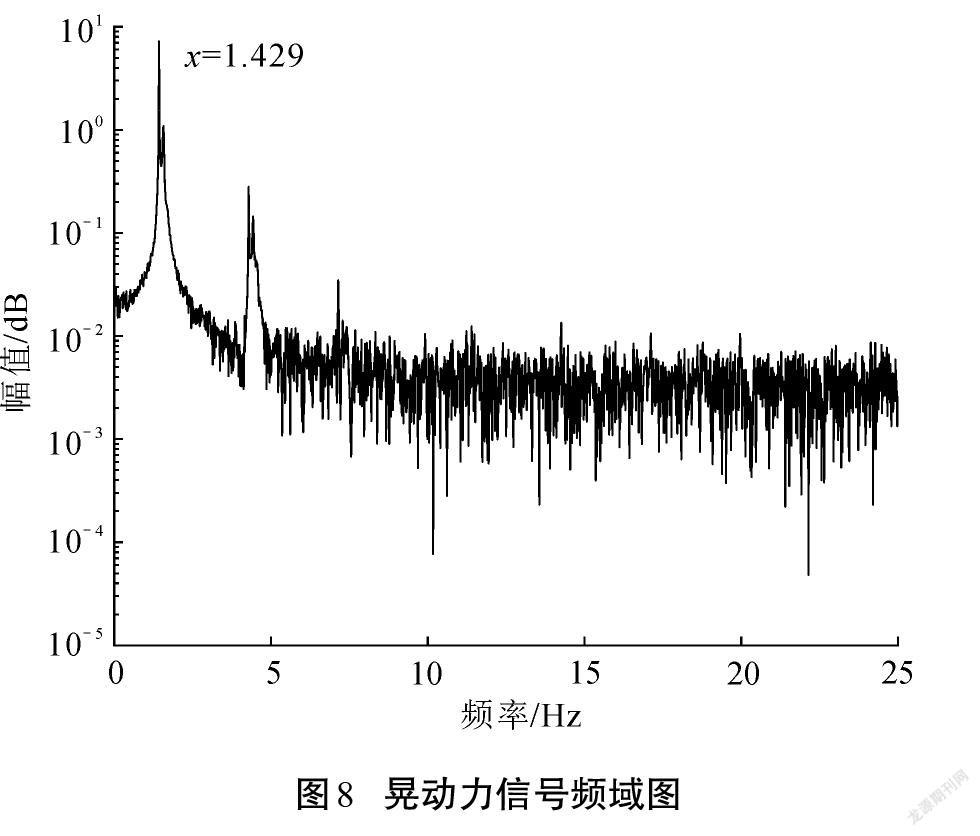
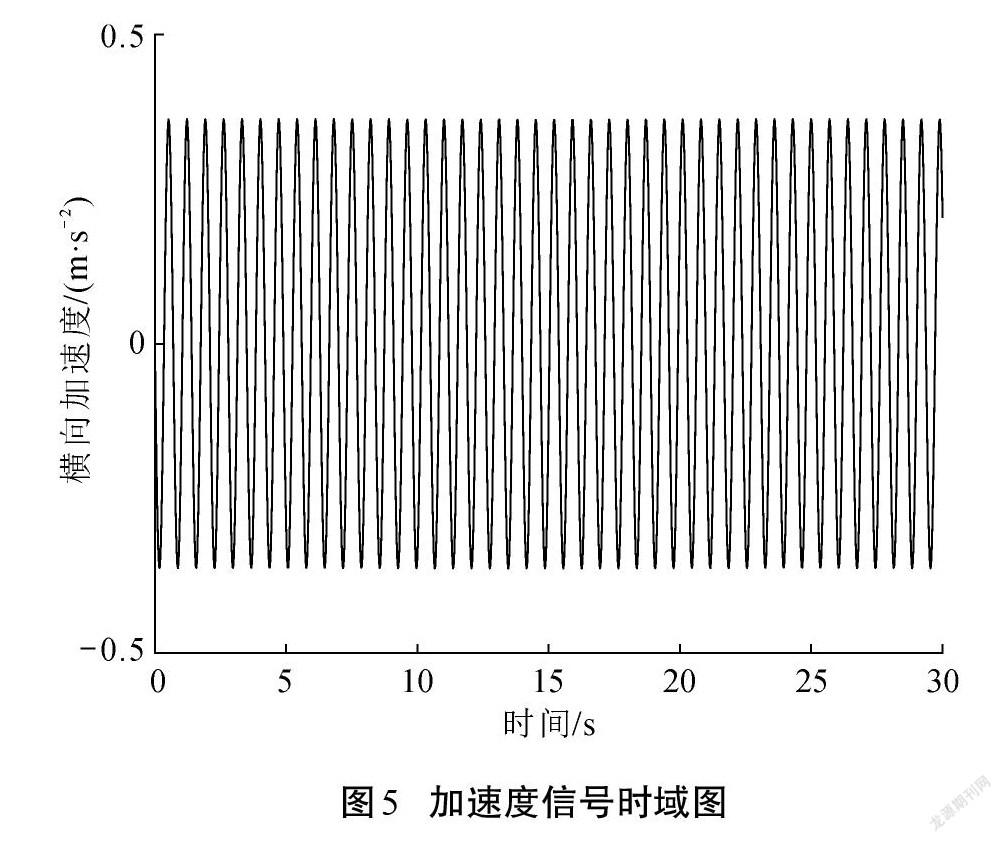
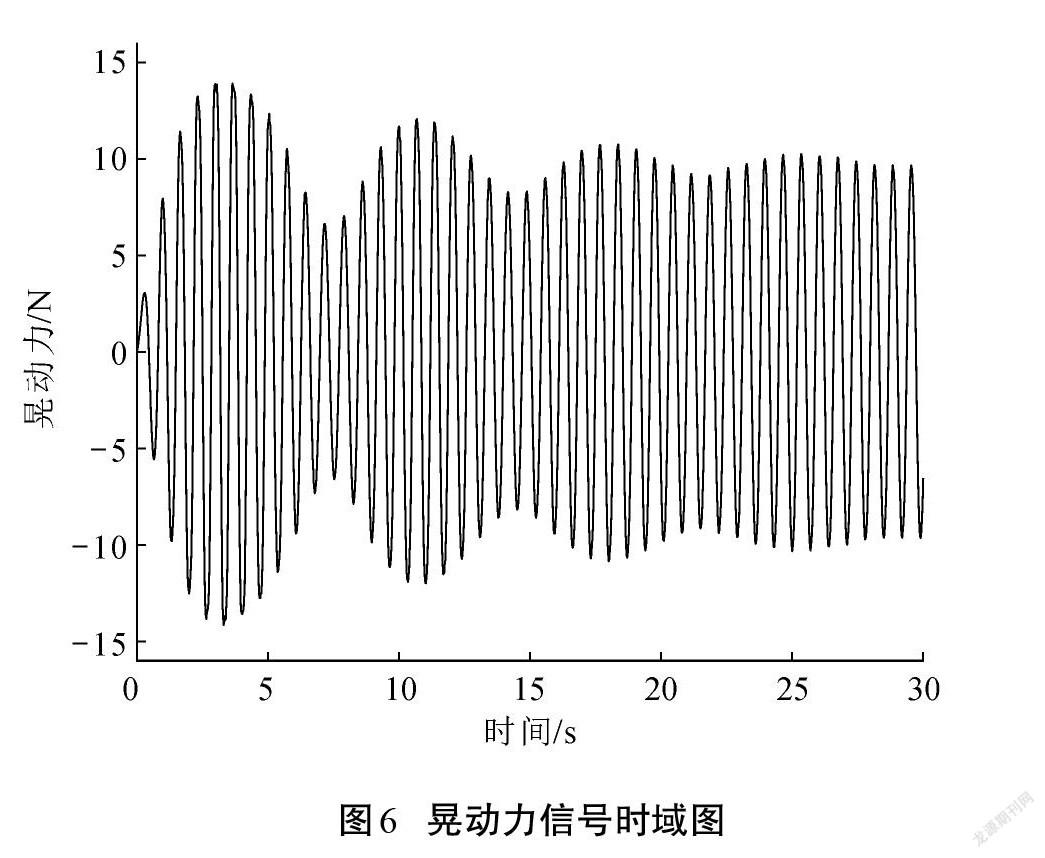
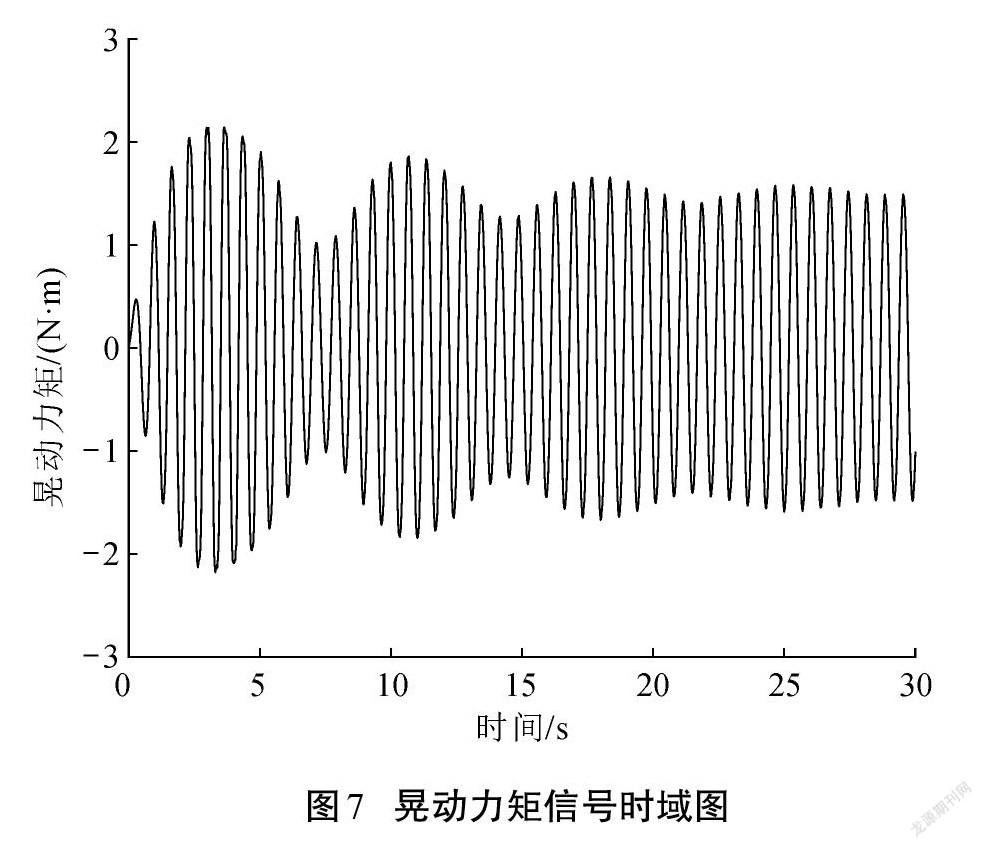
將復雜工況下充液貯箱受到的振動簡化為穩定橫向簡諧振動。為防止液體晃動發生共振現象而導致晃動行為超出小幅晃動范圍，仿真實驗中的激勵頻率范圍設置為1.43～1.52 Hz，且加速度幅值不宜過大，實現液體晃動時徑向模態為一階占優。仿真實驗完成后導出液體對貯箱的晃動力和晃動力矩信號值。以1.43 Hz激勵為例將數值模擬實驗數據進行時域圖和頻域圖的繪制，圖5—圖7分別為加速度、晃動力和晃動力矩信號的時域圖，圖8為晃動力信號的頻域轉換且經過低通濾波濾除的頻域圖。

圖6—圖7中液體晃動的拍振現象在仿真晃動實驗開始25 s左右基本消失，晃動響應逐漸由拍振過渡到標準的簡諧穩態振動，基頻約為加速度激勵的頻率值1.43 Hz。由圖8可知，當橫向加速度外激勵頻率為1.43 Hz時，充液貯箱液體晃動系統的晃動力輸出信號的一階固有頻率與外激勵頻率同步。

3? ? 參數估計和系統辨識

數值模擬仿真實驗中的液體晃動系統輸入信號和輸出信號已知，而部分系統參數未知，此類系統辨識問題屬于灰度模型參數辨識問題。

3.1? ?參數估計

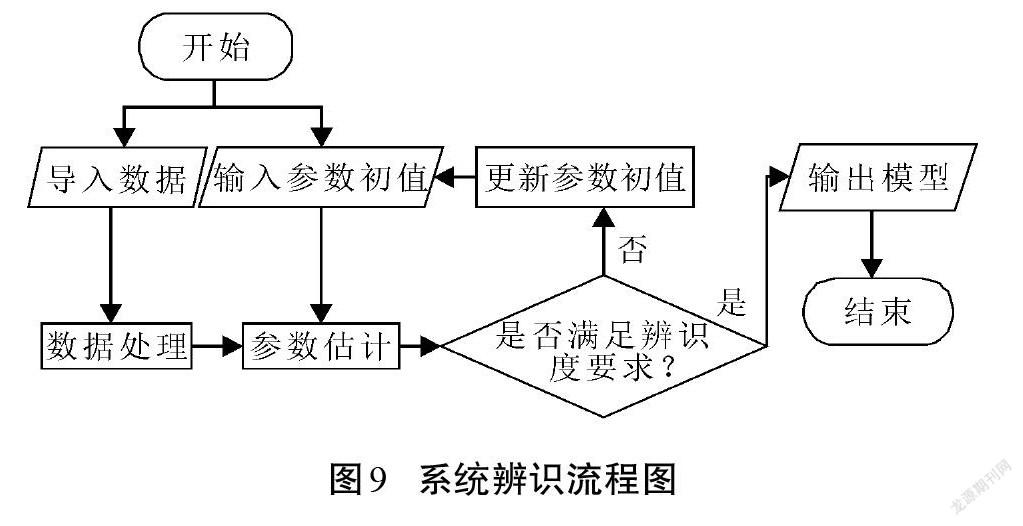
依據推導得到的狀態空間方程式（6）和輸出方程式（7），在Matlab中建立含有未知參數的初始動力學參數化模型，基于經驗設定初始化的頻率、阻尼比、輸入系數、晃動力輸出系數、晃動力矩輸出系數、直接輸出系數，導入模擬實驗數據后對灰度模型進行參數估計，系統辨識的流程如圖9所示。

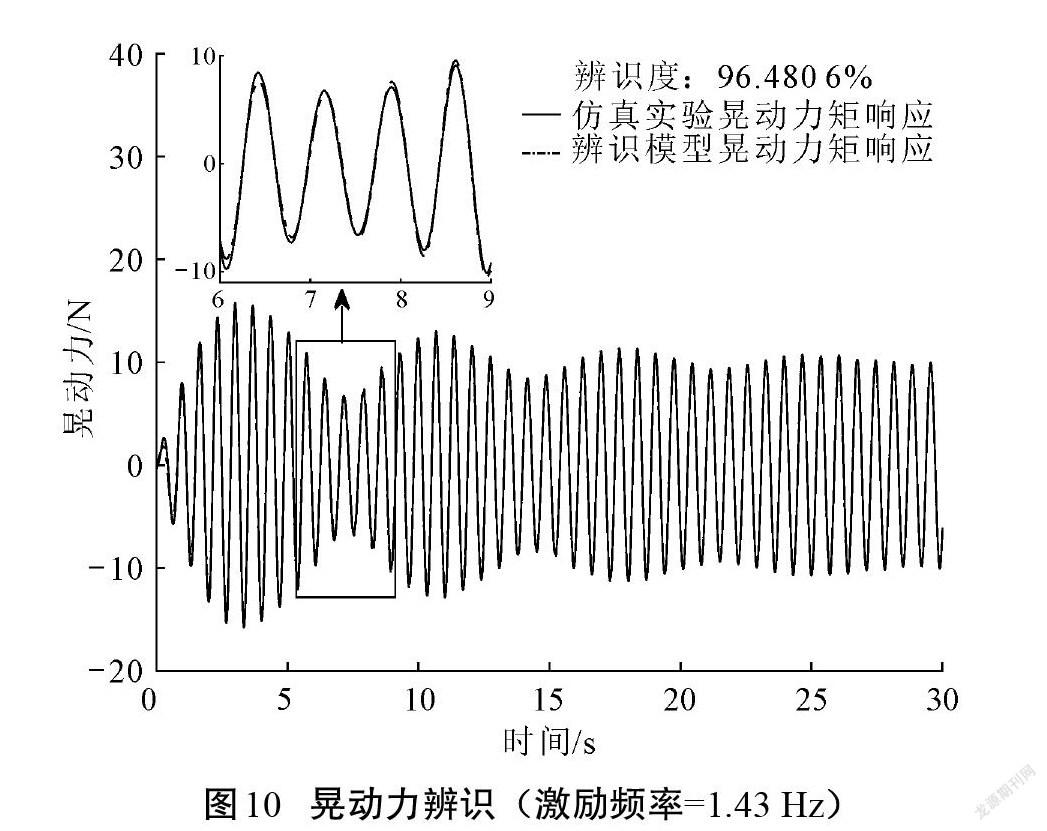
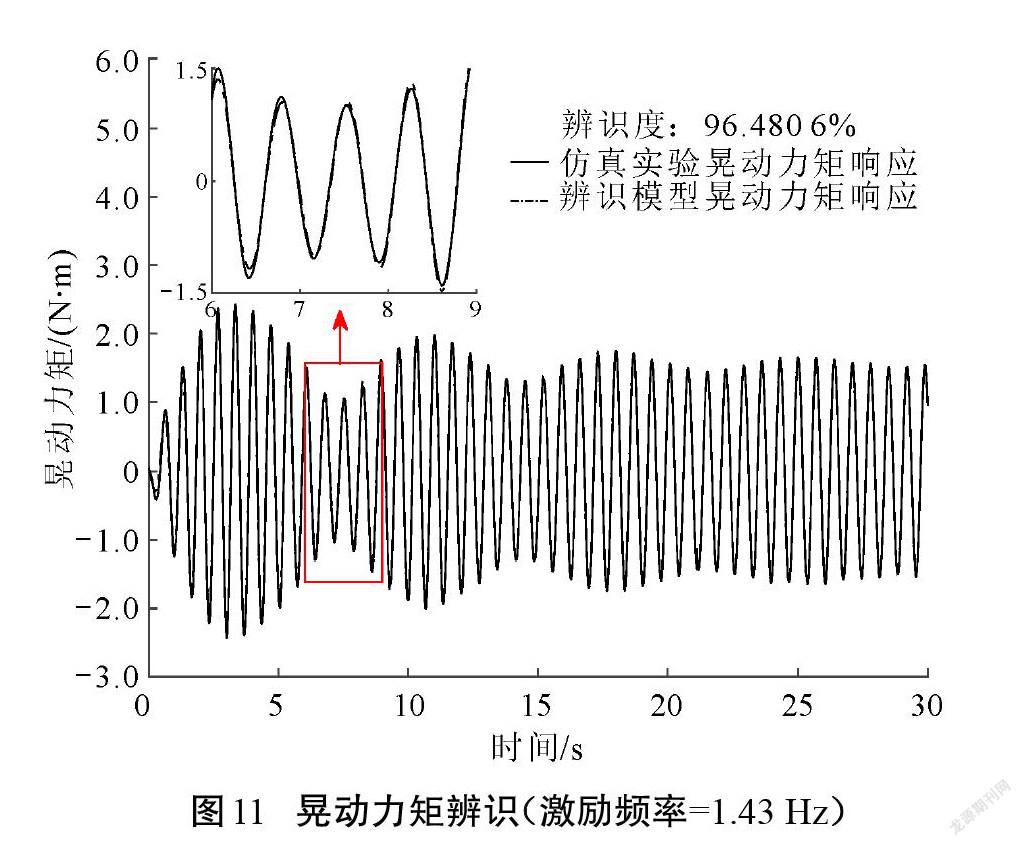
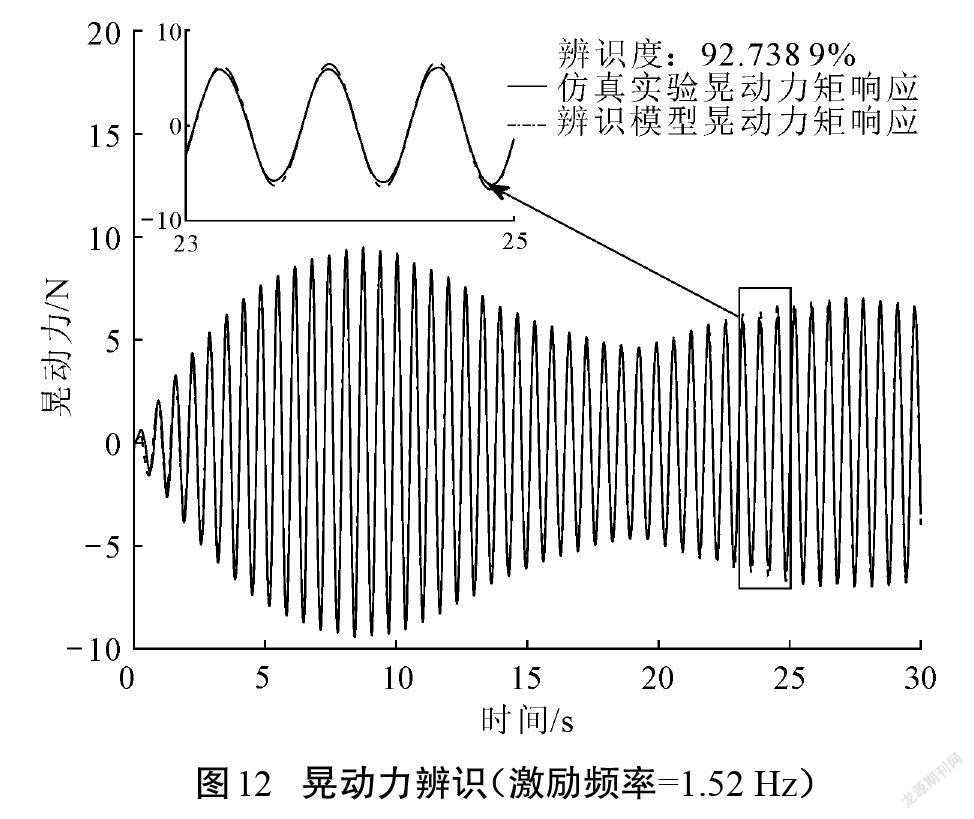
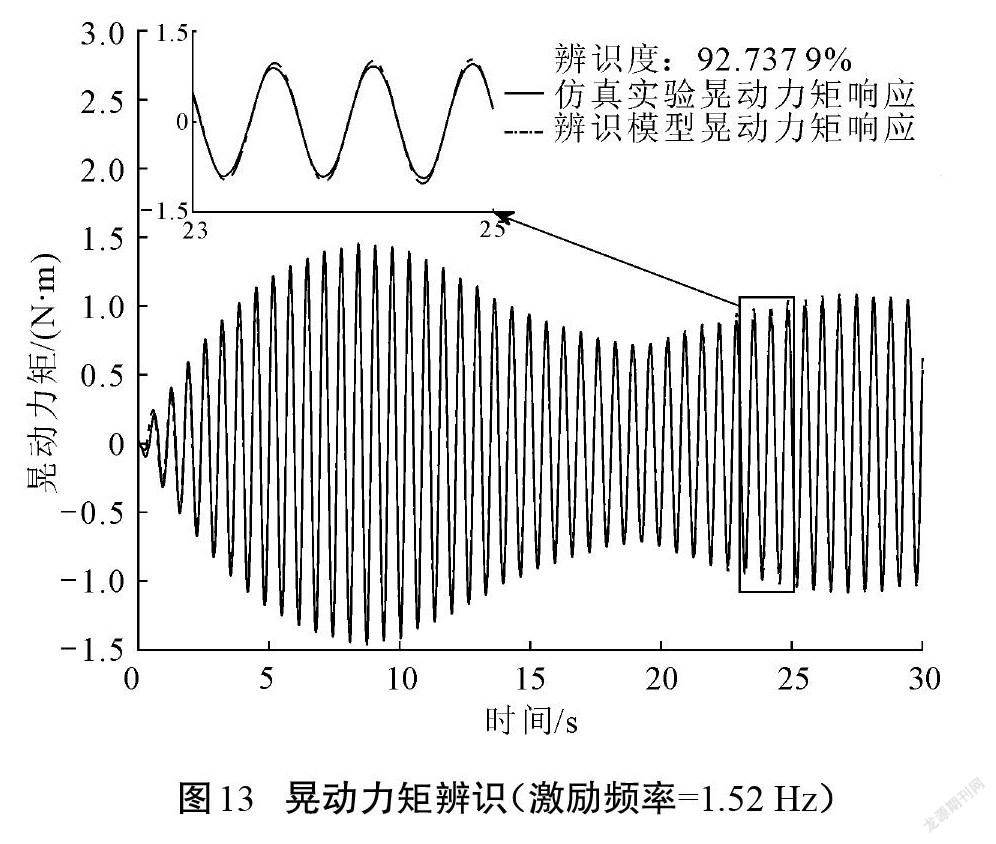
當貯液容器內充液比固定時，該系統的特征屬性唯一確定，雖然不同激勵下的系統輸出響應不同，但是輸入信號與輸出信號的轉換關系必然相同，因此，進行同一系統的不同頻率晃動模擬實驗。以1.43 Hz和1.52 Hz加速度激勵時數值仿真實驗與辨識所得模型的輸出響應結果的對比為例，如圖10—圖13所示。根據2-范數計算曲線間的距離并換算辨識度后可得：激勵頻率為1.43 Hz時，參數化模型對比數值仿真實驗的晃動力和晃動力矩輸出響應的辨識度為96%以上;激勵頻率為1.52 Hz時，辨識度為92%以上。

3.2? ?系統辨識結果

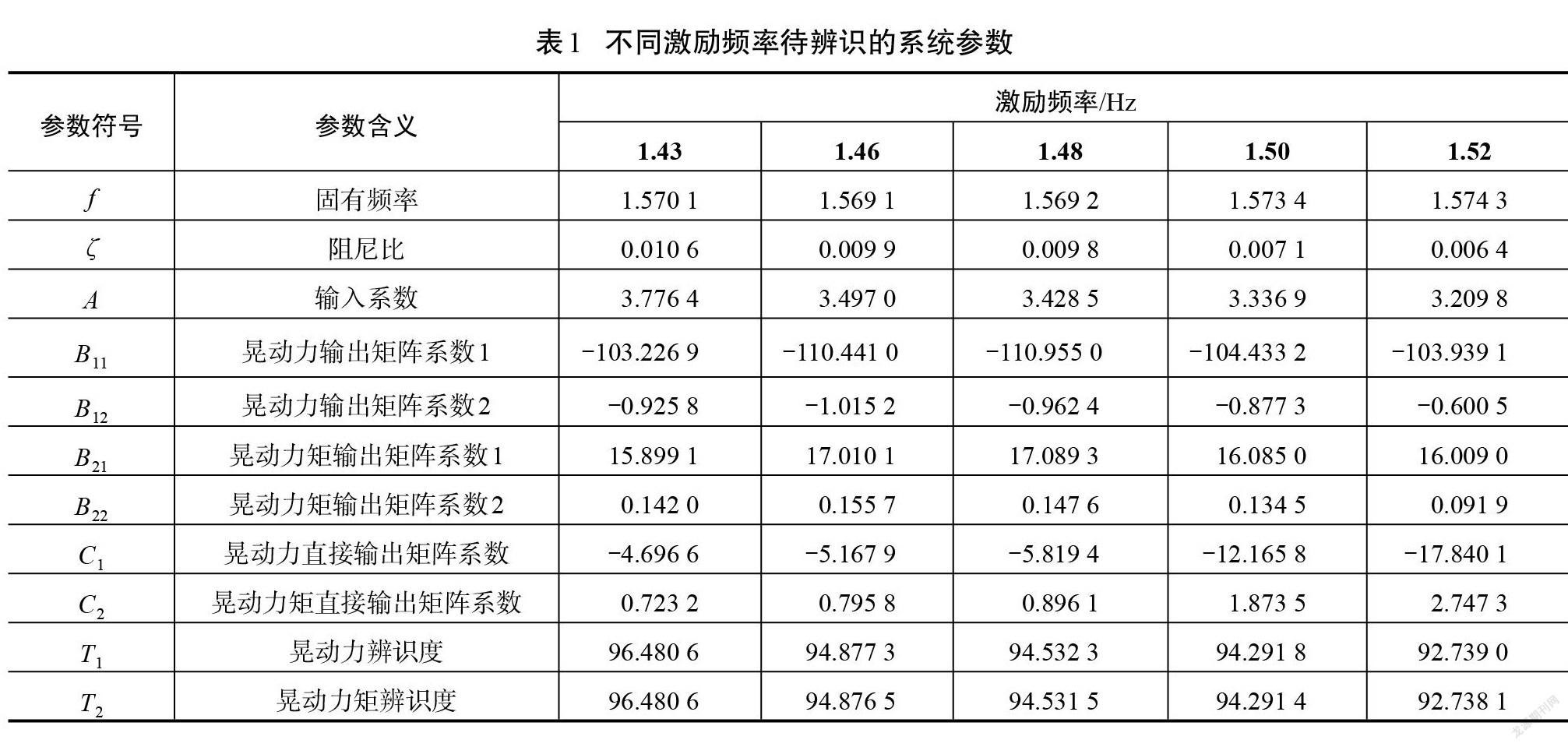
在同一激勵頻率下進行多次數值模擬實驗。為了使系統參數盡可能接近真實值，系統辨識后需要對所得同類參數進行最小二乘法的統計學處理，不同激勵頻率處理后的結果如表1所示。由表1可知，不同激勵頻率下系統的一階固有頻率[（f）]辨識為1.57 Hz左右，與自振特性實驗所得基頻接近程度達到98%以上，阻尼比[ζ=0.006～0.010]，輸入、輸出系數較為穩定且可信度高，本參數化模型對數值模擬仿真實驗晃動力和晃動力矩的輸出響應的辨識度均在92%以上。

4? ? ?結論

本文擴展充液圓柱貯箱求解區域后建立含有未知參數的充液球形貯箱晃動系統參數化動力學模型，通過CFD仿真軟件對充液球形貯箱進行自振特性實驗和不同激勵頻率下的強迫晃動實驗，依據液體壓強等式和數值仿真實驗數據在Matlab中對系統狀態向量和未知參數進行計算和辨識，研究參數化模型參數估計結果并對比分析數值模擬實驗與參數化模型的輸出響應，得出以下結論：

1）依據圓柱貯箱橫向激勵速度勢函數和波高函數中傅里葉-貝塞爾函數的正交性且圓柱空間與球形空間相切的特性，得到橫向激勵下充液球形貯箱系統的狀態空間表達式具有可行性，可將此原理類推到與圓柱貯箱相切的任意旋轉對稱貯箱。

2）自振特性實驗頻域分析能夠精準計算分析出系統的基頻，是確定系統辨識頻率初值的可靠? ? ?方法。

3）小幅簡諧橫向加速度激勵下的液體受迫晃動的數值仿真實驗結果表明：實驗前期液體晃動的“拍振”現象較為顯著，原因在于緊靠貯箱內壁面的液體和遠離壁面的液體晃動相位不同步;之后液體晃動的“拍振”現象逐漸減小直到消失，這是由于在外部激勵的持續作用下，液體晃動系統的各個子系統的相位均同步于外激勵相位。

4）本研究對不同頻率橫向簡諧加速度頻率下的充液球形貯箱內液體晃動系統進行辨識后，所得的參數化模型中參數值之間略有差別，系統基頻的辨識極佳且晃動力和晃動力矩輸出響應的辨識準確度均在92%以上，總體實現了充液球形貯箱液體晃動系統的高精度參數化等效建模的目標。

參考文獻

[1] 茅海劍， 李波， 貝紹軼， 等. 基于流固耦合的液罐車側傾穩定性研究[J].江蘇理工學院學報，2021，27（4）：56-67.

[2] 萬瀅. 液罐車輛車-液耦合動力學特性與防側翻控制方法研究[D].長春：吉林大學，2018.

[3] 黃中烈. 帶貯罐類重型車輛動力學建模與剛-液耦合特性研究[D].柳州：廣西科技大學，2019.

[4] 李超，吳文軍，周鳳霞，等. 重型罐車內液體晃動參數化數學模型辨識[J].廣西科技大學學報，2021，32（2）：65-71.

[5] 鄧傳奇. 基于ANSYS的船用雙層C型LNG儲罐結構設計研究[D].淮南：安徽理工大學，2018.

[6] 趙鶴錦. 大型儲液罐在地震作用下的響應分析[D].大連：大連理工大學，2021.

[7] 于瑾，李寶海，王求生，等.貯箱防晃擋板結構形式和晃動阻尼研究[J].導彈與航天運載技術，2021（5）：147-149，154.

[8] 劉峰， 岳寶增， 唐勇. 多充液貯腔航天器耦合動力學與姿態控制[J].宇航學報，2020，41（1）：19-26.

[9] 岳寶增，于嘉瑞，吳文軍. 多儲液腔航天器剛液耦合動力學與復合控制[J].力學學報，2017，49（2）：390-396.

[10] 孫梓煜， 岳寶增， 劉峰，等. 充液柔性航天器剛-液-柔耦合動力學研究的凱恩方法[J]. 宇航學報，2021， 42（5）：552-561.

[11] 張海濤， 孫蓓蓓. 勻加速激勵下的液體晃動力解析計算[J].振動與沖擊，2020，39（12）：158-163.

[12] 楊旦旦， 岳寶增. 低重環境下旋轉軸對稱貯箱內液體晃動研究[J].宇航學報，2013，34（7）：917-925.

[13] 陳青全. 衛星貯箱液體晃動等效力學模型參數辨識[D].長沙：國防科學技術大學，2014.

[14] 包光偉. 充液衛星平放式貯箱內液體晃動的等效力學模型[J].宇航學報，1996，17（1）：67-70，106.

[15] 苗楠，劉戰合，王曉璐，等. 考慮燃料消耗的飛機副油箱燃油晃動等效建模[J].科學技術與工程，2020，20（29）：11851-11857.

[16] 劉嘉一， 白欣然， 李曉軒. 質量-彈簧模型在儲液容器抗震分析中的應用[J].原子能科學技術，2013，47（6）：947-951.

[17] 岳寶增，祝樂梅. 攜帶晃動燃料柔性航天器姿態機動中的同宿環分叉研究[J].宇航學報，2011，32（5）：991-997.

[18] 劉峰， 岳寶增， 馬伯樂， 等. 燃料消耗下充液航天器等效動力學建模與分析[J].力學學報，2020，52（5）：1454-1464.

[19] 鄧明樂， 岳寶增， 黃華. 液體大幅晃動類等效力學模型研究[J].宇航學報，2016，37（6）：631-638.

[20] 金曉威， 賴馬樹金， 李惠. 物理增強的流場深度學習建模與模擬方法[J]. 力學學報，2021，53（10）：2616-2629.

[21] 苗楠， 李俊峰， 王天舒. 橫向激勵下液體大幅晃動建模分析[J].宇航學報，2016，37（3）：268-274.

[22] 李超， 吳文軍， 周鳳霞， 等. 重型罐車內液體晃動參數化數學模型辨識[J].廣西科技大學學報，2021，32（2）：65-71.

[23] 周鳳霞， 吳文軍， 王佐， 等. 帶貯罐類重型車輛建模與操縱穩定性研究[J].廣西科技大學學報，2020，31（2）：68-79.

[24] 王坤. 水平激勵下矩形貯箱內液體晃動力和傾覆力矩實驗研究[D].泰安：山東農業大學，2018.

[25] 吳文軍， 高超南， 岳寶增， 等. 圓柱貯箱內液體非線性穩態晃動實驗及動力學特性分析[J].宇航學報，2021，42（9）：1078-1089.

[26] 王瓊瑤. 部分充液罐車罐體內液體晃動的動力學特性研究[D].廣州：華南理工大學，2017.

[27] WANG W Y， GUO Z J， PENG Y， et al. A numerical study of the effects of the T-shaped baffles on liquid sloshing in horizontal elliptical tanks[J]. Ocean Engineering， 2016， 111：543-568.

[28] 李駿，龔思惠，張鵬飛，等. 基于FLUENT的貨車燃油箱液體晃動數值模擬[J].科學技術與工程，2020，20（34）：14152-14156.

[29] 張展博，李勝強. 圓柱水箱中水平多孔擋板對液面晃動影響的數值模擬研究[J].清華大學學報（自然科學版），2018，58（10）：934-940.

[30] 劉漢武， 張華， 胡震宇， 等. 基于SPH方法航天器含貯箱液體晃動分離動力學研究[J].中國科學：技術科學，2021，51（8）：938-947.

[31] 吳文軍. 帶多充液貯箱及機動柔性附件航天器耦合動力學研究[D].北京：北京理工大學，2015.

[32] 李遇春. 液體晃動動力學基礎[M].北京：科學出版社，2017.

System identification and parametric equivalent modeling of liquid lateral sloshing in spherical tanks

WANG Zuo， WU Wenjun*， JIANG Bingchao， GAO Chaonan

（School of Mechanical and Automotive Engineering， Guangxi University of Science and Technology，

Liuzhou 545616， China）

Abstract： The study aims at inaccuracy and incompleteness of the traditional equivalent mechanical model in describing the sloshing characteristics of the liquid in the tank. Firstly， we derive the dynamic state equation of partially liquid-filled cylindrical tank by using potential flow theory and expand the solution area of liquid sloshing in the spherical tank to the solution area of the cylindrical tank tangent to the outside based on the orthogonality condition of the Fourier-Bessel series expansion coefficient in the liquid sloshing velocity potential function and the sloshing wave height function in the equation， thus establishing a parameterized model to describe the liquid sloshing in the spherical tank. Then， we obtain the liquid sloshing force and torque of the spherical tank under lateral harmonic excitation with small sloshing through the CFD simulation experiment. Finally， we use the gray box identification function of Matlab to identify the undetermined coefficients in the established parameterized model， realizing the high-precision equivalent modeling of the liquid lateral sloshing in the spherical tank. The results show that the parameterized equivalent mechanical model can describe the natural frequency， sloshing force and torque of the liquid in the spherical tank more accurately and completely， and the identification accuracy can reach over 92%， which can give reference for the online real-time identification and practical engineering.

Key words： spherical tank; liquid sloshing; parametric modeling; CFD simulation; gray box identification; system identification

（責任編輯：羅小芬）