超高壓交叉線路空間電磁環境分析

馬明智，楊昌杰

(甘肅電通電力工程設計咨詢有限公司，甘肅 蘭州 730050)

0 引 言

超高壓輸電線路產生的工頻電磁污染引起了社會各方面關注，公眾對電磁環境問題的關注已成為電網發展的主要制約因素之一。因此，超高壓輸電線路的電磁環境問題成為線路設計的重要控制因素。目前，國內對超/特高壓輸電線路電磁環境公眾暴露限值控制標準為：工頻電場限值4 kV/m，工頻磁場限值100 μT，線下耕地、園地、牧草地、養殖水面等場所工頻電場限值10 kV/m[1]。隨著輸電網的大量建設，超高壓輸電線路工程不可避免地與相對電壓等級較低的輸電線路產生交叉跨越，而交叉區域電磁環境問題比較復雜，其計算需要建立三維模型。相對于二維場，三維空間的電磁環境計算尚未有成熟的解析方法。目前，電磁環境的計算，主要有應用于微分方程型數學模型的有限元法和應用于積分方程型數學模型的逐次鏡像法、模擬電荷法、矩量法等[2-7]。

下面采用有限元法，依托實際工程建立模型，分析超高壓交叉輸電線路下方工頻電磁場的特征，研究影響其強度的相序排列及交叉角等因素；采用屏蔽線降低電磁污染超標的交叉線路場強強度，并對屏蔽線架設位置采用混沌變參數粒子群算法(chaotic particle swarm optimization algorithm with variable parameters，CPSO)進行尋優[3]，為輸電線路設計提供指導依據。

1 研究模型

架空輸電線路空間工頻電磁場受導線對地高度、相間距離、分裂導線結構尺寸、導線布置形式、架空地線以及周圍環境等諸多因素影響。電力系統大多采用通用設計塔型，這里以同塔雙回750 kV輸電線路與單回330 kV輸電線路交叉情況為研究對象，建立相應模型，分析線路電磁環境特征以及導線不同相序排列與線路交叉角對工頻電磁環境的影響。

交叉輸電線路空間布置及相序排列方式如圖1所示。所研究模型為：上層750 kV線路采用雙回路鼓型鐵塔，導線每相為6分裂排列，相鄰子導線分裂間距為400 mm，導線采用JL/G1A-400/50鋼芯鋁絞線，地線采用1×19-13.5-1270-B鍍鋅鋼絞線；下層330 kV線路采用單回路貓頭、干字型鐵塔，導線每相為雙分裂水平排列，分裂間距400 mm，導線采用JL/G1A-300/40鋼芯鋁絞線；組合相序排列方式共6種。圖1中：A1—C1表示750 kV同塔雙回線路的1回導線，A2—C2表示 2回導線，D1、D2分別為1、2回線路地線；A3—C3表示330 kV導線，D3為其地線。根據排列方式不同，上層750 kV可排出Ⅰ～Ⅵ六種，下層330 kV可排出1～6六種。

在輸電線路三維電磁環境計算中，采用有限元法，將空間網格剖分成許多細小四節點三棱錐(四面體)單元，空間場量的計算可表示為：

(1)

(2)

式中：L為空間三棱錐劃分數量；Ui為第i個三棱錐頂點場量；Nei為第i個三棱錐的插值基函數；pi、qi、ri、si、Ve為由三棱錐頂點坐標計算出的系數。

工程用麥克斯韋方程組微分型式可表示為：

?·D=ρ

(3)

?·B=0

(4)

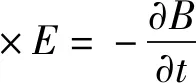
(5)

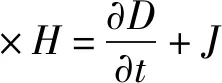
(6)

引入矢量磁位，滿足

B=?×A

(7)

相應有關場量的輔助方程為

D=εE,B=μH,J=σE

(8)

式(3)至式(8)中：E為電場強度；D為電位移；B為磁通密度；H為磁場強度；ρ為電荷密度；ε為介電常數；μ為磁導率；σ為電導率；J為電流密度；t為時間。

以麥克斯韋微分方程組導出用于有限元處理電磁問題的微分方程，計算過程能考慮任意塔形和導線布置，準確計算空間任一點的電磁場強度數值解。

2 交叉線路電磁感應影響要因分析

為考察交叉線路三維電磁環境，在圖1所示的空間模型中，以線路下方離地面1.5 m處某平面為考察區域，將目標區域劃分成N×N的小方形域，求取每個域的電磁場加權平均值，權重系數應反映每個小區域的重要程度。區域目標函數F可表示為

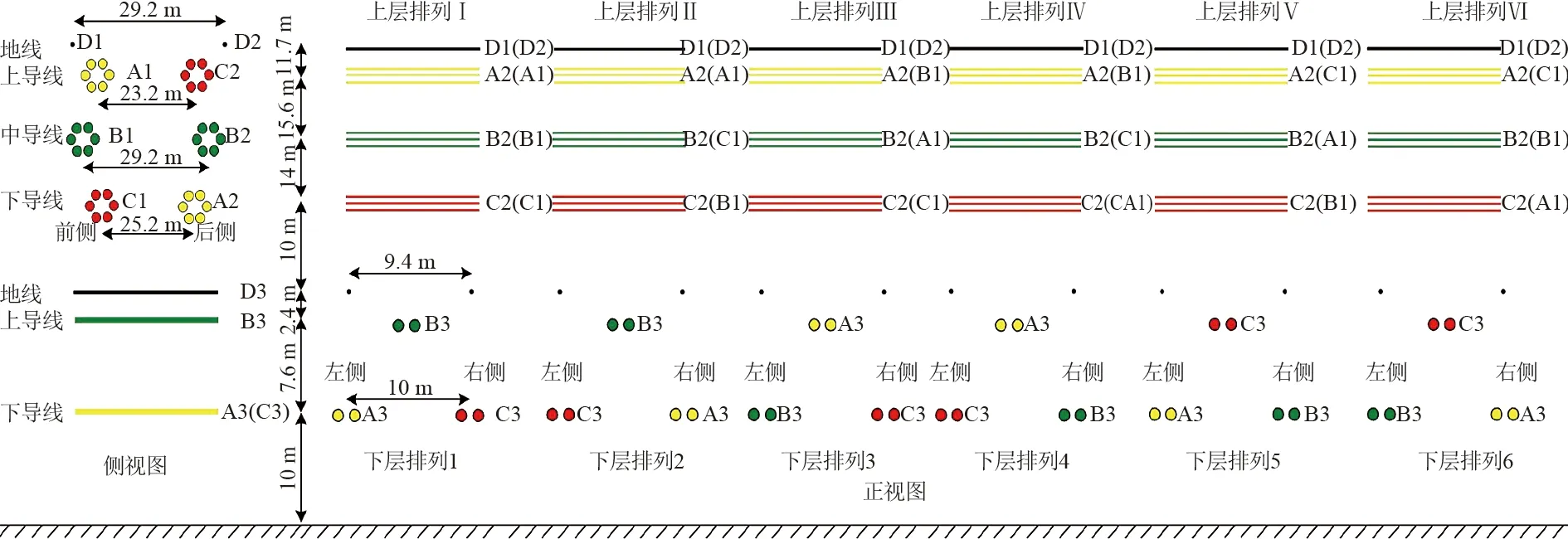
圖1 交叉輸電線路空間布置方式及相序排列

(9)

式中：Ej為第j個小方域電場強度或磁感應強度；kj為權重系數，∑kj=1，kj∈[0,1]。

2.1 導線相序排列方式對工頻電磁場影響

2.1.1 導線相序排列方式對工頻電場影響

對圖1所示的交叉輸電線路相序排列方式進行組合，根據式(9)求線下-40 m～40 m的正方形區域目標值F，線路交叉角取90°，計算結果如表1所示。

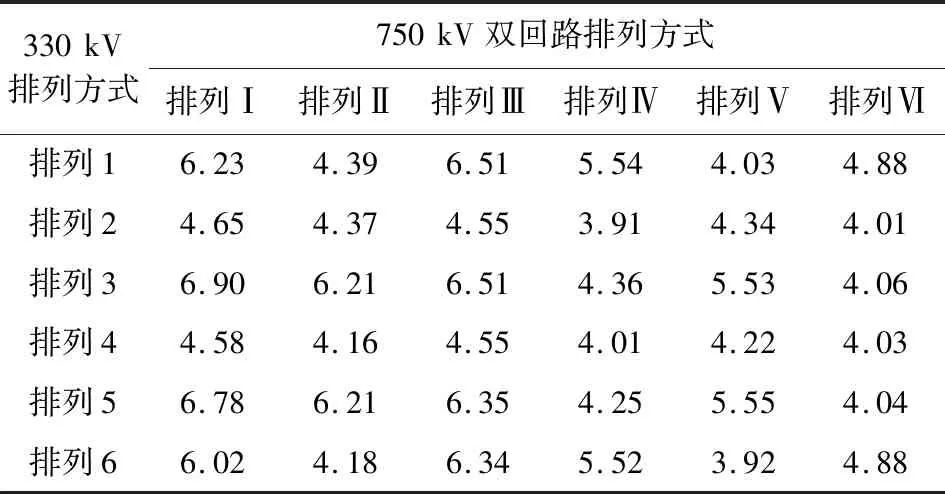
表1 不同相序排列方式下區域電場強度 單位：kV/m

圖2繪制出了考察區域內電場強度E值。

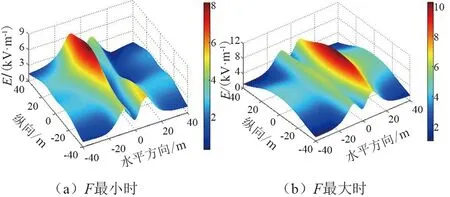
圖2 交叉線路下方E值

由表1及圖2可以看出，交叉輸電線路線下工頻電場受上層相序排列方式影響較大。當上層雙回線路采取同相序排列時，線下加權平均場強都較大(4.58～6.9 kV/m)；當上層雙回線路采取逆相序排列時，線下加權平均場強都較小(4.01～4.88 kV/m)，實際工程中可以采取上層線路逆相序排列方式。

2.1.2 導線相序排列方式對工頻磁場影響

與工頻電場相似，求解線下區域目標值F，計算結果如表2所示。

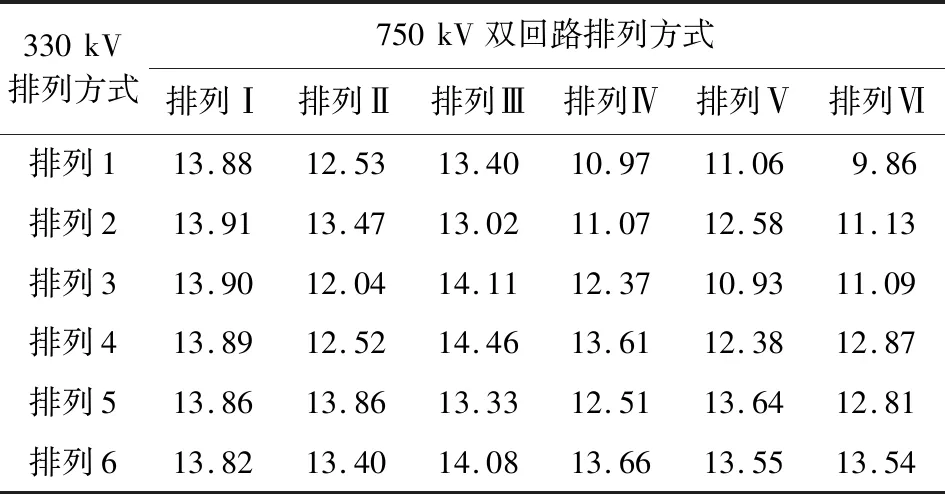
表2 不同相序排列方式下區域磁感應強度 單位：μT

圖3繪制出了考察區域內磁感應強度B值。

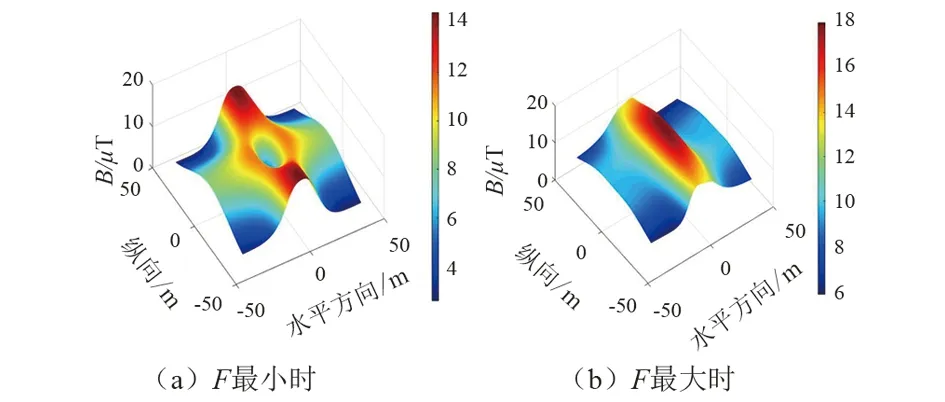
圖3 交叉線路下方B值

由表2及圖3可以看出，交叉輸電線路線下工頻磁場受上層相序排列方式影響較大。當上層雙回線路采取同相序排列時，線下加權平均場強都較大(13.82～13.91 μT)；當上層雙回線路采取逆相序排列時，線下加權平均場強都較小(9.86～13.54 μT)。因此，在實際工程中推薦采取雙回路逆相序排列方式。

2.2 線路交叉角對工頻電磁場影響

利用2.1所得結果，考察工頻電場區域目標值F最小時的相序布置方式，區域目標值F隨角度變化情況。目標區域函數值F隨線路交叉角變化情況如圖4所示。

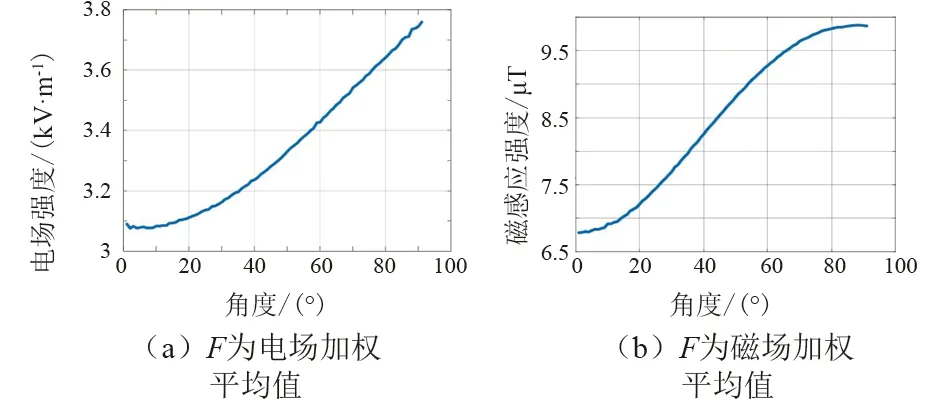
圖4 目標區域函數值F隨線路交叉角變化情況

由圖4可見，隨交叉角的增大，目標區域函數值F也相應增大。為提高輸電通道本質安全，相關部門要求重要輸電線路交跨角不宜小于45°，其線路下方電磁環境如圖5所示。

圖5 交叉角45°時線路下方電磁環境

3 屏蔽措施

由上述內容可知，交叉線路下方電場強度受相序排列組合及交叉角影響，區域目標值F最小時，線下場強呈現的馬鞍面加權平均場強不超標，而沿下層線路方向單側場強超出標準要求。因此，采用在導線下方架設屏蔽線的方式減小地面工頻電場。對屏蔽線架設位置采用CPSO算法進行尋優，實現屏蔽優化設計。

3.1 CPSO算法

標準粒子群優化算法(particle swarm optimization,PSO)的數學描述為：假設在一個d維的目標搜索空間中，有m個代表潛在問題解的粒子組成的一個種群S={X1,X2,…,Xm}，該種群中的第k個元素Xk={xk1,xk2,…，xkd}，表示第k個粒子在d維空間的一個矢量點。用Pkd(pk1,pk2,…,pkd)記錄第k個粒子自身搜索到的最優點。而在這個種群中，搜索到的最好值記為g，則Pgd=(Pg1,…,Pgd)。可以用Vk(vk1,vk2,…,vkd)表示第k個粒子的速度。PSO算法采用式(10)實現。

(10)

式中：rand()產生(0,1)之間的隨機數；w為慣性權重系數；c1、c2為每個粒子的學習因子；t-1、t為粒子運動時刻。

慣性權重系數取以時間為變量的非線性函數，如式(11)所示。

w(t)=(wmax-wmin)×tan(0.875×

(11)

式中：titer為最大進化代數；t為當前進化數；K為控制因子；wmax、wmin為慣性權重區間上、下限。

PSO算法存在易陷于局部最優、優化計算精度低、后期收斂慢的缺點。故根據混沌運動的隨機性、遍歷性等特點，采用混沌控制參數變化的粒子群優化算法進行尋優計算。混沌(chaos)是由確定方程得到的非確定隨機運動狀態，具有隨機性、便利性及規律性等特點，能在一定范圍內不重復地遍歷所有狀態。邏輯斯諦方程是一個典型的混沌系統，其公式為

xn+1=μxn(1-xn)

(12)

式中：μ為混沌控制參數;xn為混沌變量，xn∈[0，1]。

CPSO算法具體的流程描述如圖6所示。

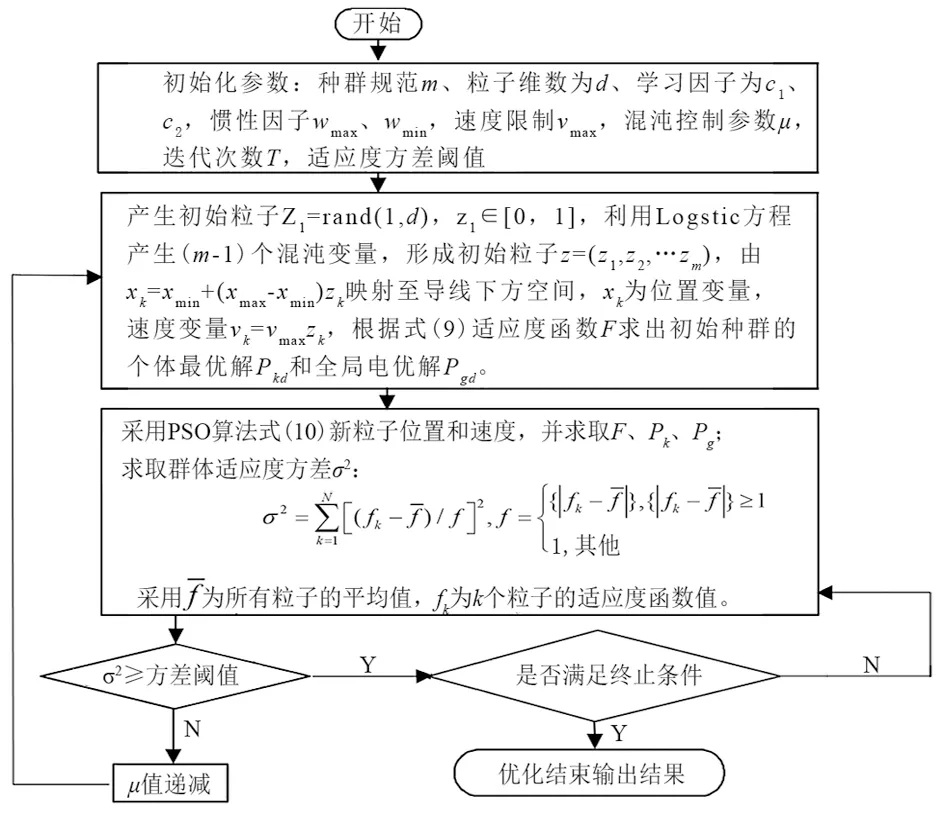
圖6 CPSO算法流程

由于混沌變量的遍歷性和隨機性有助于增強種群的搜索能力，在算法運行過程中，根據種群的收斂情況，動態地減小式(12)中混沌控制參數μ，降低混沌運動對種群結構的破壞，擺脫陷入局部最優的困境。

3.2 CPSO算法優化屏蔽仿真實驗

以區域目標函數F作為CPSO算法的適應度函數，并沿下層線路方向架設屏蔽線，屏蔽線高度lh在[0，20]區間取值，水平位置lp在[-30，30]區間取值。分別對架設單根及兩根屏蔽線的位置進行尋優，得到適應度函數收斂曲線，如圖7所示。由圖可見，混沌變參數粒子群優化算法在保證算法能擺脫局部最優的基礎上，明顯提高了收斂性能。

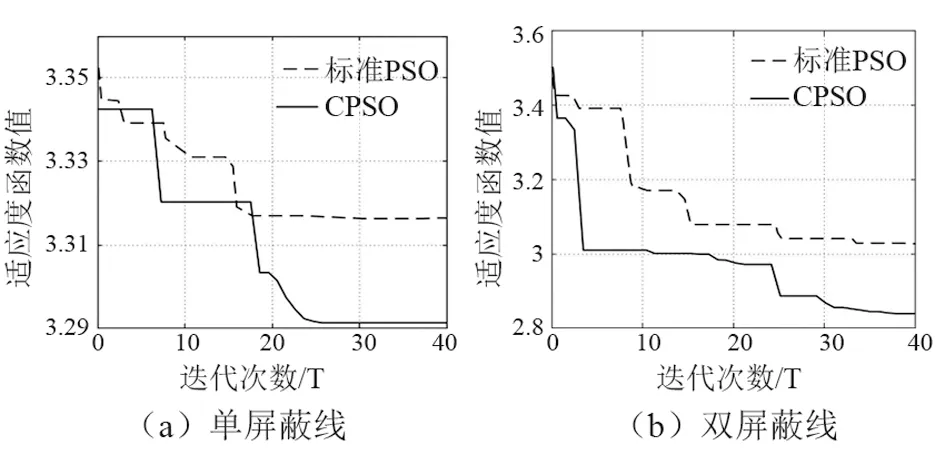
圖7 適應度函數收斂曲線

對屏蔽線架設位置通過CPSO算法尋優，得到的架設位置為：單屏蔽線lh=2.32 m、lp=-8.49 m；雙屏蔽線lh1=3.12 m、lp1=7.80 m、lh2=2.32 m、lp2=-8.50 m。架設屏蔽線后，考察-40 m～40 m正方形區域內，交叉線路下方場強如圖8所示。

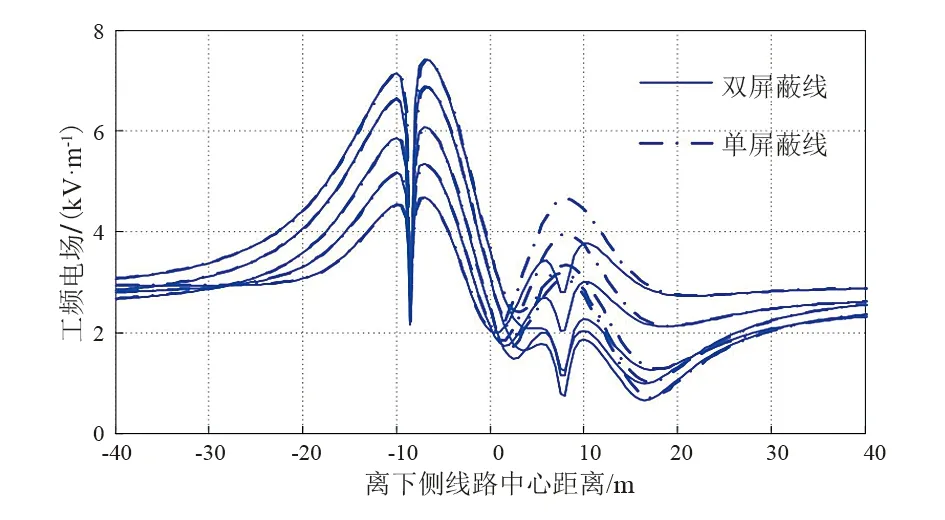
圖8 架設屏蔽線后線路下方不同橫斷面E值

架設屏蔽線后交叉線路下方E值如圖9所示。可以看出，CPSO尋優位置基本在畸變的馬鞍面電場峰值附近，架設單屏蔽線可以將加權場強均值從3.91 kV/m降至3.29 kV/m，而架設雙屏蔽線降可至2.85 kV/m，場強峰值位置處降低較明顯，屏蔽效果良好。

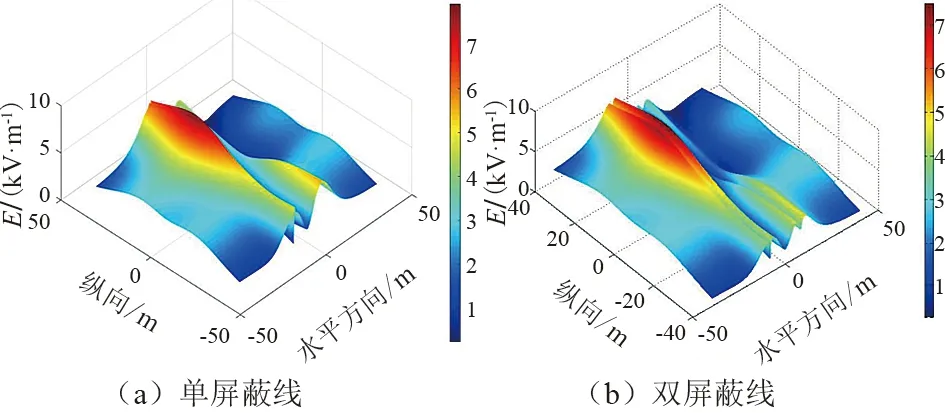
圖9 架設屏蔽線后交叉線路下方E值

4 結 論

上面采用有限元法，通過一系列仿真實驗，在構造的區域目標函數基礎上，研究線路相序布置和交叉角對空間電磁環境的影響，并給出可用于工程的相序排列方式及交叉角建議：為簡化設計難度，在滿足設計要求時，上層雙回路宜采用逆相序布置，交叉角可適當減小，以降低空間電磁污染。

采用架設屏蔽線的方式改善地面電磁環境，并引入混沌變參數粒子群算法，對屏蔽線架設位置進行目標尋優，尋優過程中，動態減小混沌控制參數值，使算法在迭代過程中逐步減弱混沌運動，進而在保留混沌粒子群優化算法優點的基礎上，又增添了粒子群體的多樣性，實現快速跳出局部最優點，尋找全局最優解。通過CPSO算法對屏蔽線架設位置尋優，實現區域電磁環境屏蔽效果最優。