多狀態系統測試建模與測試點選取方法

王 鵬，于永利，李星新，劉晨光，孫也尊

(1.陸軍工程大學(石家莊校區) 裝備指揮與管理系，石家莊 050003;2.中國人民解放軍32382部隊，北京 100072;3.中國人民解放軍32200部隊，遼寧 錦州 121000)

測試性定義為產品能及時準確地確定其狀態(可工作、不可工作或性能下降)，并隔離其內部故障的一種設計特性。需要指出的是，測試性不僅包括系統故障的測試，還包括正常和退化狀態的測試。然而，對于系統可測試性的研究往往更多地關注于故障測試而在退化狀態測試方面的研究較少。目前常見的測試性模型主要是在相關性模型基礎上建立的，如邏輯模型、結構模型、信號流模型、多信號模型及混合診斷模型等[1]。這些測試性模型能夠實現系統故障與測試相關關系的描述，但其測試分析過程均是在二態系統基礎上進行的，忽略了系統的多狀態特性，從而難以實現系統退化狀態的測試性分析。

相較于二狀態系統(只考慮正常和故障兩種狀態)，多狀態系統(Multi-state system, MSS)考慮了系統及元件從正常到故障之間的一個或多個退化狀態，能夠通過定量的轉移概率描述系統狀態與元件狀態、系統狀態與系統故障之間的關系，多狀態信息對揭示復雜系統潛在的失效機理和規律至關重要，有利于提高系統故障診斷與預測效率，降低診斷成本[2]。目前，在多狀態系統模型的基礎上，研究主要集中在多狀態系統可靠性建模與分析[3-9]、可靠性優化設計[10-14]、維修管理策略[15-20]等方面，這些研究通過分析系統的狀態轉移關系，結合初始狀態求得系統的狀態分布，從而對系統的可靠性進行分析與優化設計、制定維修策略，而對多狀態系統測試優化問題的研究相對較少。

針對二態系統的測試優化問題，國內、外學者進行了廣泛研究并提出了許多優化方法，主要包括基于信息理論的排序方法[21-23]和基于組合優化的搜索算法[24-26]。前者主要利用信息熵來定義測試對于故障檢測和故障隔離的有用程度，并以此作為測試的權重，優先選擇權重高的測試，直到滿足測試性指標要求為止；后者以測試代價最小為目標函數，以測試性指標要求為約束條件建立數學模型，然后采用智能優化算法求解。

由于考慮了介于正常和故障的中間狀態，多狀態系統測試不僅要考慮系統的故障診斷問題，還需考慮系統及元件中間狀態的診斷問題。而多狀態系統的測試優化問題就是通過分析系統測試與系統狀態之間的關系，在滿足測試性指標要求的情況下，綜合權衡測試代價與系統狀態信息獲取問題。測試與系統狀態的相關分析是進行系統測試優化的基礎。因此，本文首先分析多狀態系統特點，對多狀態系統測試性進行建模；其次在所建模型基礎上，分析了系統的狀態-測試相關關系；最后提出了考慮故障檢測率、故障隔離率與狀態檢測率的測試點選取方法。

1 狀態測試相關建模

1.1 多狀態系統描述

設一個多狀態系統由n個元件組成，其中任意元件m具有hm+1個狀態，則其狀態空間按照由差到好的順序依次排列描述為sm={0,1,…,hm} ，其中0狀態為元件的故障狀態，hm狀態為元件的正常工作狀態，其余狀態介于故障與正常之間。與元件m的狀態空間相對應的性能水平為gm={gm0,…,gmhm}，其中gmk為元件m處于狀態k(k∈sm)時的性能水平。元件m處于不同狀態下的概率可以表示為集合pm={pm0,…,pmhm} ，其中pmk為元件m處于狀態k下的概率。系統的狀態為S(t)={s1(t),s2(t),…,sn(t)}，其中si(t)∈si。設Ln={g10,…,g1h1}×…×{gn0,…,gnhn}為所有系統元件性能水平的組合空間；整個系統可能出現n個狀態，系統處于狀態i(i∈{1,…,n} )時的性能表示為vi，M={v1,…,vn}為系統性能水平空間，以Gi(t)表示t時刻元件i的性能水平，映射φ(G1(t),…,Gn(t)):Ln→M表示為元件性能水平空間與系統性能水平空間的轉換關系，則系統性能水平函數描述為

V(t)=φ(G1(t),…,Gn(t))

(1)

也稱為系統的結構函數，表示元件性能與系統性能之間的傳遞關系，它由系統的結構關系以及元件性能屬性共同決定。

1.2 MSS測試建模

在二態系統的測試性建模方面，以信息流模型、多信號模型以及混合診斷模型為主的相關性模型得到了廣泛應用[1]。多信號模型通過獲取系統的故障-測試相關信息，以滿足規定的故障檢測率和故障隔離率為約束條件，進而搜尋代價最小的測試。對多狀態系統測試而言，不僅需要測試能夠發現并隔離系統故障，還需獲取系統的狀態信息。因此，在進行多狀態系統測試性設計時，需要對多狀態系統的狀態傳遞過程進行分析，獲得包括故障信息在內的系統狀態-測試相關信息。由于多信號模型是對系統結構的建模，無法得到系統功能相關的狀態信息，因此不適用于多狀態系統的測試建模分析。本文提出一種基于結構和功能建模的多狀態系統測試相關模型，該模型根據產品層次化結構和功能設計信息，以功能為底層建模對象，通過功能的性能指標判斷各功能的狀態，并以性能狀態作為各單元功能相關的輸入用以動態描述功能的作用關系，從而實現系統狀態-測試相關關系的描述。由于認知和隨機的不確定性的存在，建模過程中考慮了系統發生故障后的傳播不確定性、測試的不確定性以及模型認知機理的不確定性。對于系統單元性能的故障判斷問題，通過專家經驗、歷史數據、相似性判斷3種經驗知識對系統故障進行診斷。總體建模思路如圖1所示。

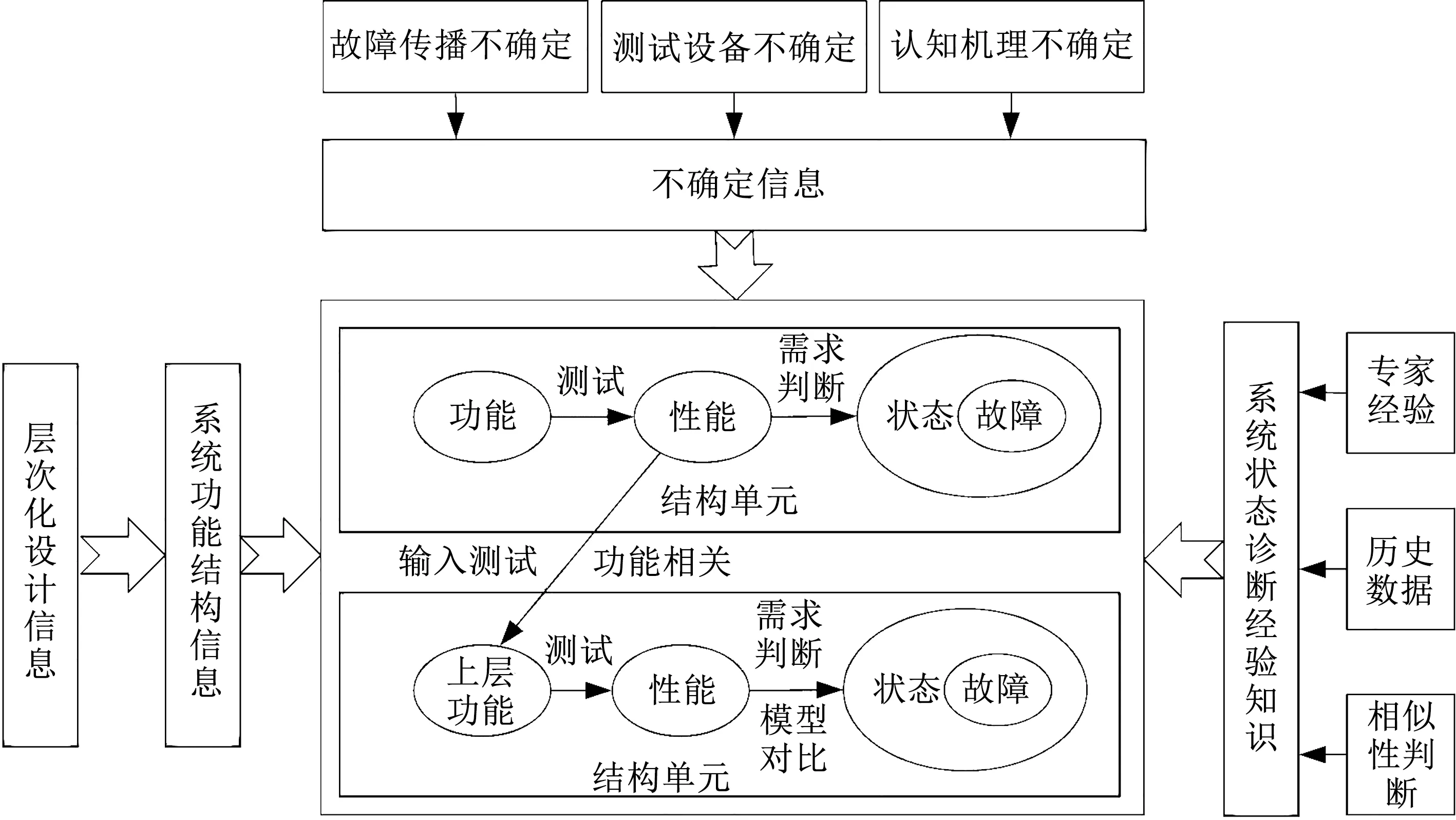
圖1 建模總體思路Fig.1 General idea of modeling

系統測試模型可以描述為一個有向圖G={C,CF,FM,E,T,D}，其中C={c1,…,cn}表示系統n個結構單元的有限集合；CF={cf1,…,cfr}是系統組成單元r個功能的有限集合，每個功能依賴于相應的系統組成單元；FM={fm1,…,fml}是系統l個故障模式的有限集合，每個故障模式依賴于相應組成單元的功能；E={eij}表示由功能i指向功能j的有向邊的集合，描述系統功能的流向關系；T={t1,…,tk}表示系統中k個可用測試點的有限集合，測試點用于測試某個功能的輸出信號；D=[dij]是單元功能-測試依賴關系矩陣，以功能為行，測試為列，若從功能i的輸出信號能夠經過有向邊到達測試j，則dij=1，否則dij=0，在考慮到故障傳播的不確定性和測試的不確定性情況下，若功能i的輸出信號能夠經過有向邊到達測試j的概率為pij，測試tj的可靠性為σtj，則dij=pijσtj。

2 多狀態系統測試選擇方法

2.1 狀態與測試問題考慮

系統功能的輸出信號是否符合規定的性能值是判斷系統是否故障的依據。因此，通過在功能輸出位置加入測試點進行測試，根據得到的結果是否符合規定的性能指標即可判斷系統是否存在故障。然而，雖然測試結果能夠判斷系統是否存在故障，卻無法定位故障源。要判斷單元的功能狀態，不僅需要獲得該功能的輸出信號，還應獲取相應的輸入信號。要獲取系統所有單元功能的輸入輸出，所需測試代價高昂，此外在很多情況下(限于測試所占有的空間，質量或者技術條件)，單元的功能輸出信號無法獲取。因此，多狀態系統的測試需要考慮兩方面問題：1)如何建立系統測試與單元功能狀態之間的關系。2)如何選擇能夠滿足系統要求的測試。

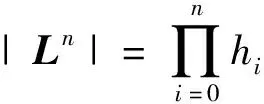
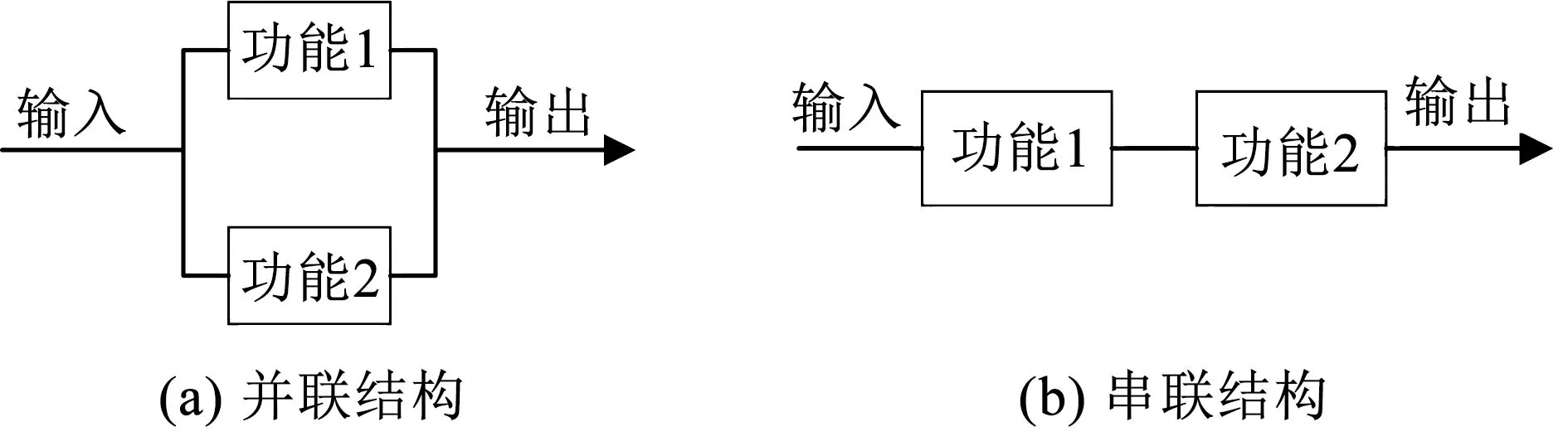
圖2 多狀態系統結構Fig.2 Multi-state system structures

通過上述分析可知，除同質系統外，僅憑系統輸出測試無法確定系統的每個狀態。為了確定系統狀態，首先需要對系統各狀態與測試的關系進行分析，其次考慮增加合理的測試，對多個測試結果進行綜合分析判斷系統狀態。

2.2 狀態-測試相關分析

為了建立測試與功能狀態的關系，設系統中測試點ti相關的功能集合為RCFti={cfj|dji=1,cfj∈CF}。在這里定義系統測試點ti的測試取值空間為

H(ti)=φi(g1,…,gn)

(2)

式中φi(·)為測試結構函數，表示各單元功能的性能水平空間與測試取值空間的映射關系，與時間t無關，由各元件到測試點的結構關系及性能屬性確定。若單元功能cfm處于狀態smk時測試ti的取值與該功能不在狀態smk時的取值空間無交集，則測試ti可以檢測狀態smk。則測試ti能夠檢測的狀態集Hh(ti)滿足：

(3)

式中H(ti|gmk)為功能cfm在狀態smk下，測試ti的取值空間。

當測試ti=r∈H(ti)時，與其相應的功能狀態組合空間為

(4)

若功能狀態組合空間中的元素包含某些共同的狀態，則這些功能狀態可以被測試ti確定，也就是說測試ti取值r時可以確定這些功能狀態組合，那么，可確定的組合功能狀態集表示為

(5)

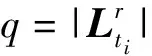
可以證明Hs(ti)?Hcs(ti)。設smk∈Hs(ti)，φi(gim,…,gmk,gjn)=r，則在φi(gik,…,gmx,gjp)=r的集合[gik,…,gmx,gjp]中，必有x=k。這是因為，根據Hs(ti)定義，若x≠k，H(ti|gmk)∩H(ti|gmx)=?，即與φi(gik,…,gmx,gjp)=r矛盾，因此必有x=k。由此可得smk∈[sik,…,smk,sjp]∩[sik,…,smx,sjp]，進而可以得到Hs(ti)?Hcs(ti)。

為了描述測試與測試之間的關系，設RCFtj?RCFti，說明tj所測試的功能是ti所測試功能的低層級功能，此時測試點ti的測試取值空間可以通過H(tj)進行計算，即

H(ti)=φi-j(gcfk,…,gcfp,H(tj))

(6)

式中：cfk,…,cfp∈RCFi-RCFj，φi-j(·)為測試tj到測試ti的測試結構函數。若H(ti)取某個值時，能夠確定H(tj)的取值，則H(ti)能夠確定H(tj)取該值時所確定的組合狀態；若H(ti)取任何值都不能確定H(tj)的取值，則H(ti)不能夠確定H(tj)所確定的組合狀態。當測試tj=b∈H(tj)，測試ti=a∈H(ti)能夠確定cfk,…,cfp∈RCFi-RCFj中的某些狀態，則在測試tj已知情況下，由測試ti所確定的組合功能狀態可以表示為

?a∈H(ti),b∈H(tj)}

(7)

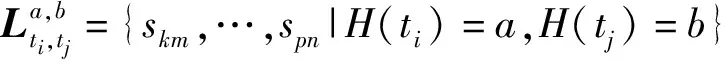
測試集Ts能夠確定的組合狀態集包括單個測試所能確定的組合狀態以及Ts中各個測試聯合所能確定的組合狀態，實際上對于測試集來說，由測試ti所確定的組合狀態只與該測試緊鄰的低層級測試有關，因為其低層級測試取值是包括了更低層級測試取值與相關功能狀態的結果。因此，測試集Ts所能確定的組合功能狀態集可以表示為

(8)

測試結構函數描述了測試與功能狀態以及高層功能測試與底層功能測試之間的關系。多狀態系統中零件、部件、子系統、系統的功能狀態空間是有限離散的，因此通過結構函數能夠確定低層零件功能狀態與系統功能狀態之間的映射關系，從而使系統低層功能狀態通過結構函數往高層功能狀態傳遞過程中是收斂的，避免了系統狀態空間爆炸的問題。

2.3 測試點選擇方法

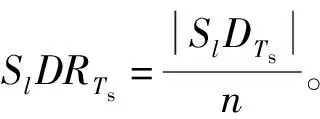
(9)

式中，p(Sl)為系統處于狀態組合Sl下的概率。

(10)

式中p(sm0)為功能cfm處于0狀態(即故障狀態)的概率。

定義系統中與功能cfi相關的測試集RTi={tj|dji=1,tj∈T}，設測試集Ts能夠隔離的功能故障集合為FITs，有FITs={cfi|cfi∈FDTs,RTi⊕RTj≠0,?cfj∈FDTs}。則測試集Ts下，系統的故障隔離率為

(11)

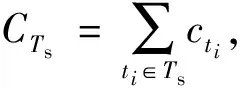
(12)

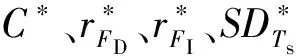
2.4 MSS測試優化算法

當多狀態系統包含元件數量較多時，一般需要較多的測試點以滿足系統的測試要求。假設系統中有N個可用測試點，那么根據每個測試點選用與否，系統具有2N個測試組合。因此，當N值較大時，應用枚舉法對每一個測試組合進行分析，將變成一個工作量巨大的NP完全問題。有必要采用一種啟發式的搜索算法尋找到滿足要求的測試組合。

本文以經典遺傳算法為例重點說明應用啟發式算法求解最佳測試點的過程。種群的選擇規則即適應度函數的選擇是遺傳算法的核心內容。由于故障檢測率、故障隔離率、狀態檢測率以及測試代價在不同的情況下，設計人員可能會有不同的偏重，適應度函數可由下式給出：

f(Ts)=λ1·FDRTs+λ2·FIRTs+λ3·SDRTs

(13)

可通過調整系數λ1、λ2、λ3的取值，分別實現對不同測試指標的偏重。當λ3取值為0時，測試優化僅考慮故障檢測率和故障隔離率，與二態系統的測試優化相同。

算法包括如下步驟：

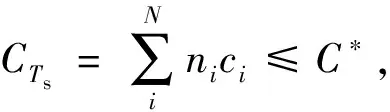
2)產生滿足測試代價要求的初始群體。根據步驟1)隨機生成一定數量的N位二進制碼，使得N位二進制碼所代表的相應測試集的測試代價滿足CTs≤C*。組成初始群體作為進化的第一代。

3)選擇種群個體。根據適應度函數判斷個體優劣，具有相同適應度函數的個體以測試代價最小為最優，將種群中制定數目的最差評價個體用相同數目的最優個體取代。

4)交叉和。對選擇后的種群中每一對個體以一定的概率交換他們之間的部分染色體，當交換后形成的新個體對相應測試代價滿足要求時，用新的個體對代替舊的個體對；如果不滿足測試代價要求則保留原來的個體對。對群體中的每一個個體以某一個概率改變其中某一些基因，只有當新的個體滿足測試代價要求時，用新的個體取代舊的個體，形成下一代種群。

5)經過步驟3)、4)，判斷種群中的最佳個體(適應度函數最大的個體，當適應度函數相同時，取測試代價較小的個體為最佳個體)是否滿足用戶對故障檢測率、故障隔離率、狀態檢測率要求，或者達到最大進化代數，如果是就找到最優個體并結束，否則轉到步驟3)。

3 模型實現與分析

本文所研究方法適用于多狀態系統相關可靠性數據已知的情況，而對于系統元件多狀態數據未知的系統，存在應用上的限制。在許多工程系統中多狀態數據統計結果未知的情況下，本文僅做了理論上的分析。

3.1 算例說明

圖3所示為某數據處理系統，該系統包含9個組成單元、15個功能及相應的15個可用測試點。每個功能包含3種狀態，即si={0,1,2}，處于每個狀態的概率為pi={0.1,0.3,0.6}，其中i∈[1,15]。以每個功能的數據處理能力作為其性能指標，表1列出了每個功能在各狀態下的性能。

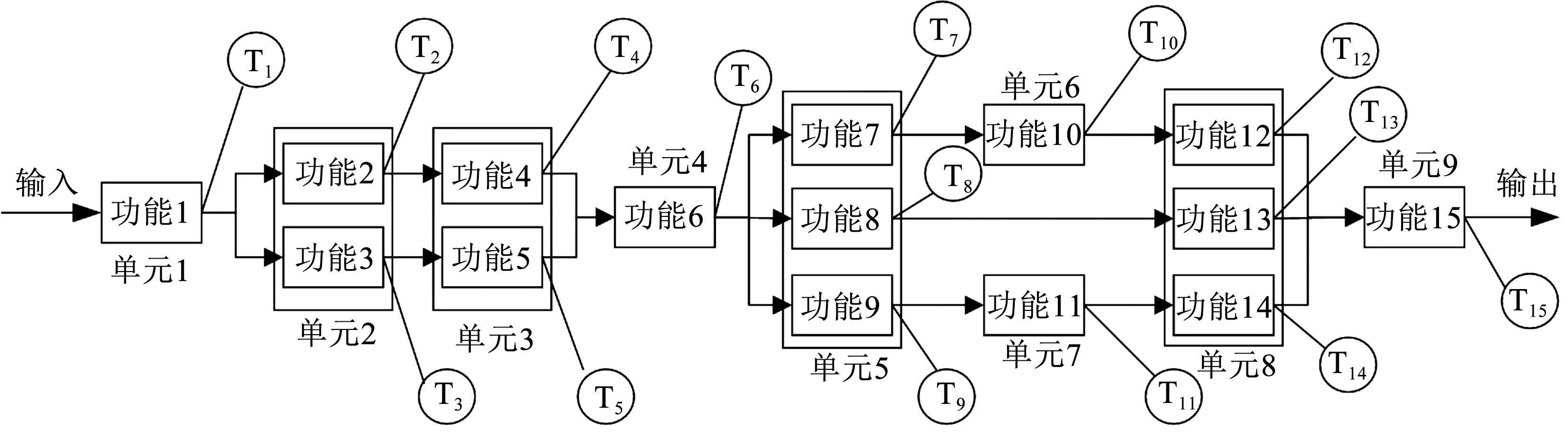
圖3 某數據處理系統Fig.3 A data processing system

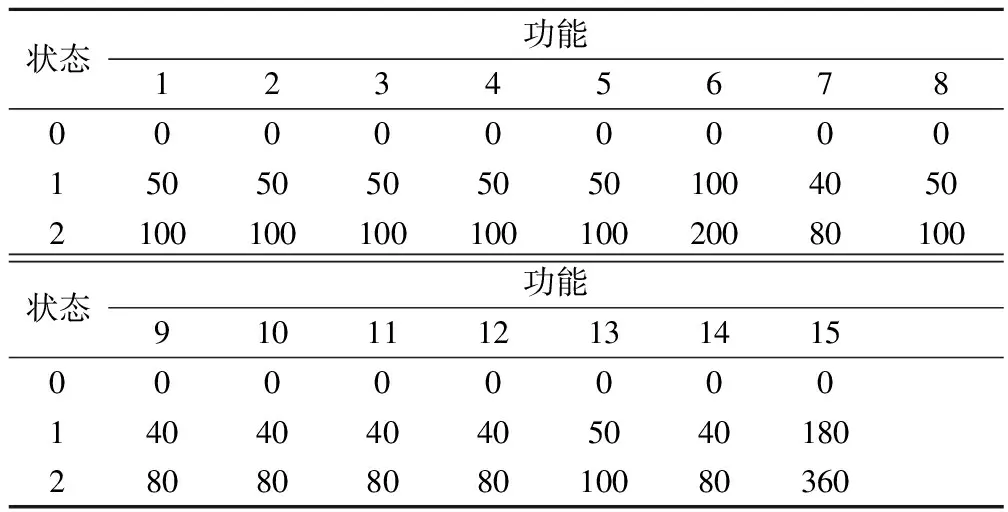
表1 各功能在不同狀態下的性能Tab.1 Performance of each function in different states

由系統數據傳輸特性可知，由式(1)可得系統的結構函數為

V(t)={minG1(t),min[G2(t),G4(t)]+min[G3(t),

G5(t)],G6(t),min[G7(t),G10(t),G12(t)]+

min[G8(t),G13(t)]+[G9(t),G11(t),G14(t)],G15(t)}

(14)

實際應用中的不確定信息是作為已知信息輸入的，為了方便計算，這里假定故障的傳播及測試是可靠的，可以得到功能-測試依賴關系矩陣為

(15)

由式(2)可得各測試取值空間見表2。

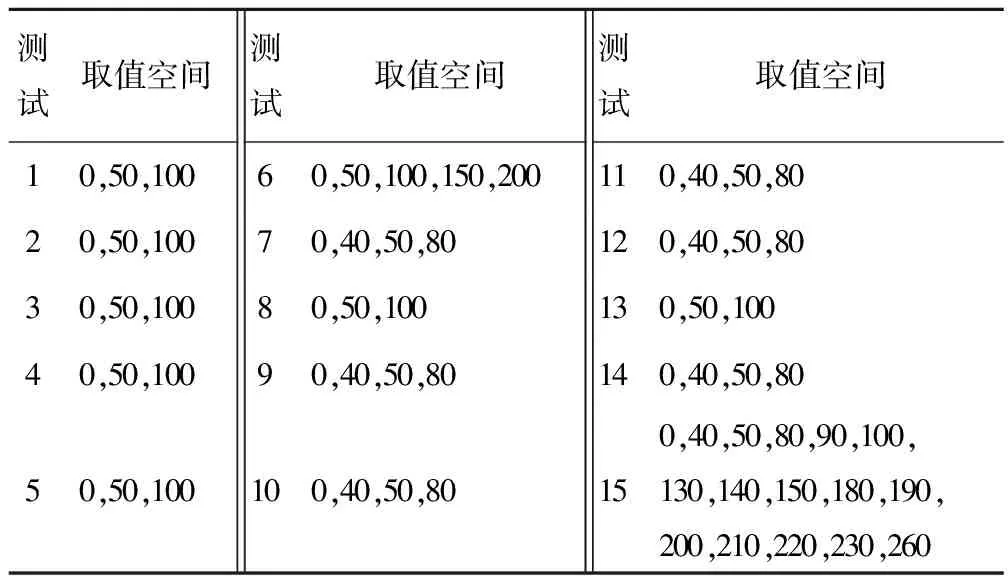
表2 各測試取值空間Tab.2 Value range of each test

由各測試的取值空間及式(4)、(5)得到各測試可確定的狀態集及相應測試值見表3。

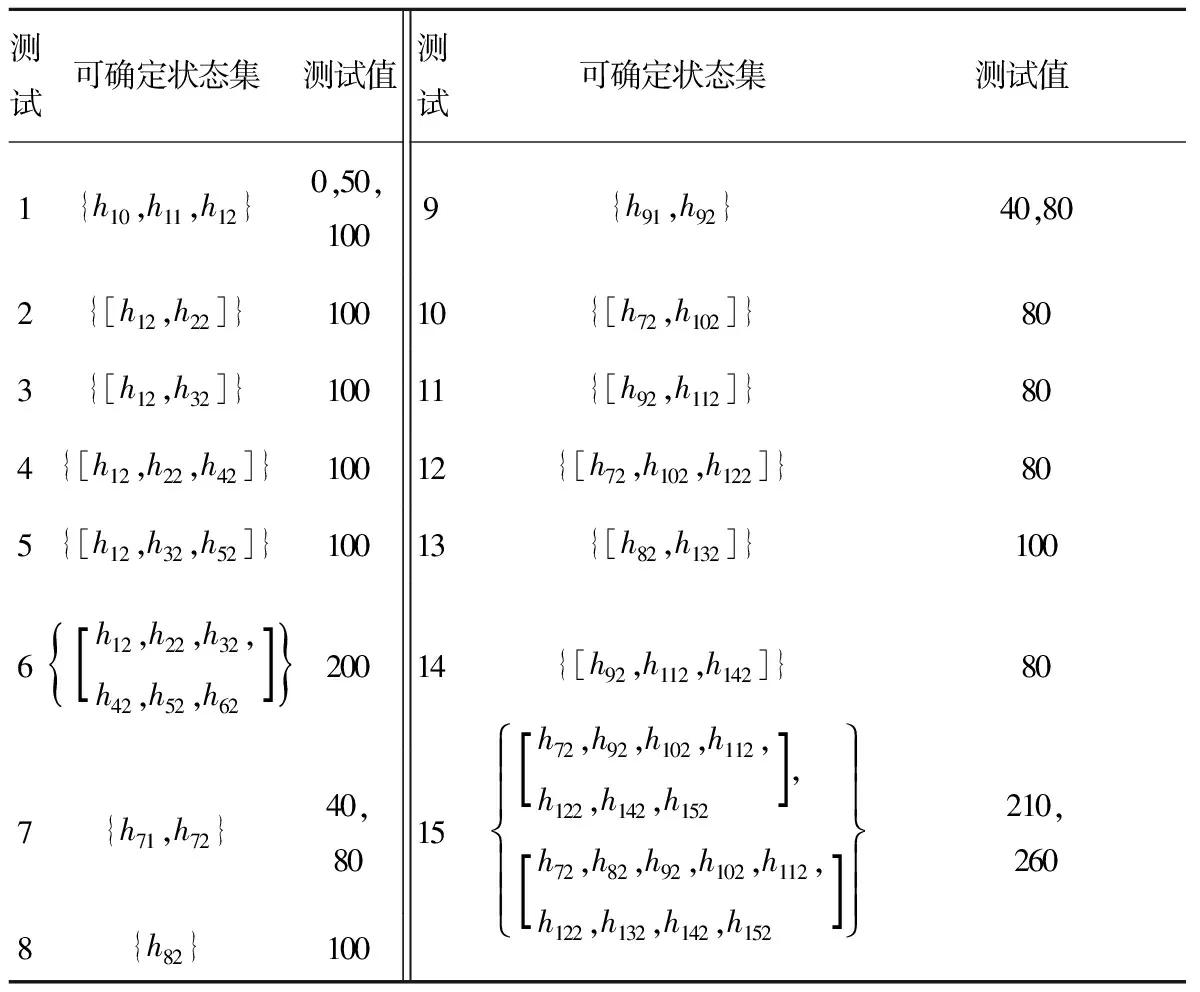
表3 各測試可確定的狀態集及相應取值Tab.3 Detectable state sets of each test and corresponding values

3.2 結果分析

設適應度函數中λ1=λ2=λ3=1/3，各測試點的測試代價為cti=c=1，則對于測試集Ts?T，可根據式(9)～(11)分別計算出狀態檢測率，故障隔離率和故障檢測率。根據適應度函數式(13)計算相應測試集的適應度。圖4所示為不同測試代價要求下，所求得最佳測試集的測試代價、以及對應的適應度函數值、系統故障檢測率、故障隔離率和狀態檢測率。可以看出，隨著測試代價要求的增加，最佳測試集的測試代價不斷增加，狀態檢測率不斷增加，最終的FDR和FIR均為1，而SDR未達到1，說明即使選擇了所有可用測試點，系統狀態也不是完全可知的。

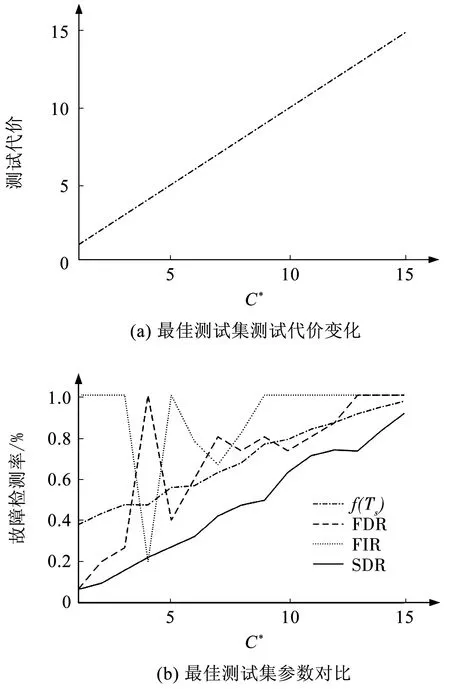
圖4 多狀態系統各參數隨測試代價要求的變化Fig.4 Changes in parameters of multi-state system with test cost

為了對比本文方法所求最佳測試集與二態系統考慮下所求的最佳測試集，設置λ1=λ2=0.5，λ3=0時，此時由于僅考慮了故障檢測率和故障隔離率，得到的最佳測試集就是二態系統下的最佳測試集，其在不同測試代價要求下的最佳測試集參數如圖5所示。可以看出，系統僅需要12個測試點就能夠完全檢測并隔離系統故障。隨著測試點增多，狀態檢測率基本呈正增長，而當故障檢測率和隔離率逐漸收斂到最大值1后，狀態檢測率呈現隨機波動現象，說明二態系統的測試點選取并沒有考慮到狀態的測試問題。

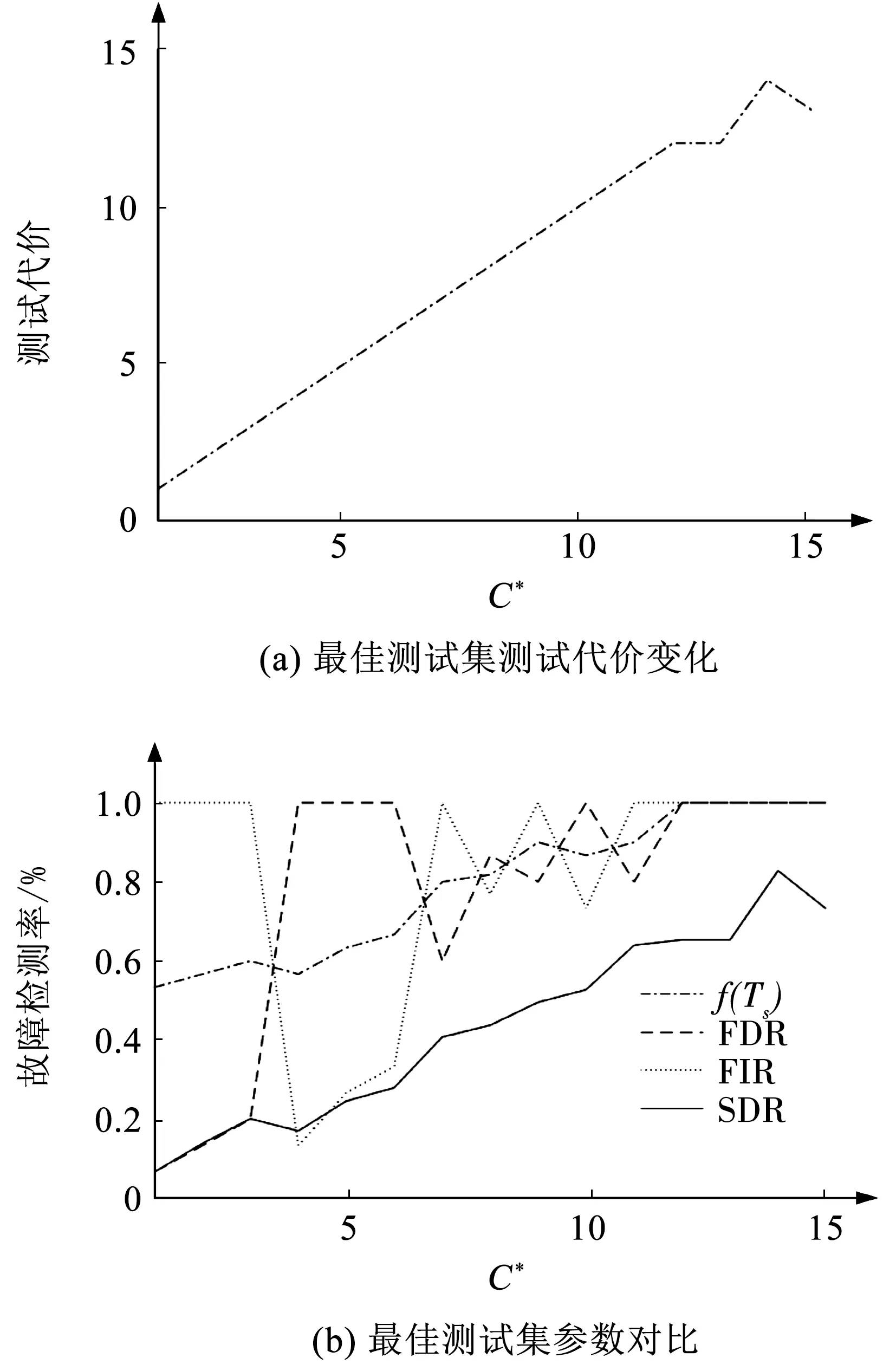
圖5 二態系統各參數隨測試代價要求的變化Fig.5 Changes in parameters of binary system with test cost

表4所示為不同測試代價要求下，考慮多狀態系統時應用GA算法得出的最佳測試集及相應參數值。表5所示為不同測試代價要求下，考慮二態系統時應用GA算法得出的最佳測試集及相應參數值。

表4 多狀態系統最佳測試集及參數值Tab.4 Optimal test set and parameter values of multi-state system

表5 二態系統下最佳測試集及參數值Tab.5 Optimal test set and parameter values of binary system

通過對比表4、5，可以發現在相同的測試代價限制下，多狀態系統的最佳測試集能夠獲得較高的SDR值，且多狀態系統與二態系統的FDR和FIR之和相差不大。對比表4、5的最后一列說明，在測試代價無限制的情況下，本文方法所得的最佳測試集在保證測試性指標(FDR和FIR)的情況下，能夠獲取更高的系統狀態檢測率。

4 結 論

1)在分析現有二態系統測試模型基礎上，結合多狀態系統相關理論，對多狀態系統測試性建模方法以及結構、功能和測試的相關描述方法進行了研究，實現了基于結構和功能的多狀態系統測試性建模。

2)對狀態測試問題進行了分析，并分別對單個測試能夠檢測的狀態集與測試集組合能夠檢測的狀態集的計算方法進行了研究，在此基礎上提出了狀態檢測率的概念實現了退化狀態的測試性指標量化。

3)考慮到系統測試性設計與分析中包含故障的測試性問題，因此在多狀態系統測試點選取過程中綜合考慮了故障檢測率、故障隔離率和狀態檢測率，并提出了測試代價約束下的多狀態系統測試點選取方法。

4)考慮到復雜系統測試點較多時，最佳測試集的搜索是一個NP完全問題，因此給出了基于GA算法的啟發式最佳測試集搜索方法。應用一個數值案例說明了多狀態系統測試建模與測試點選取過程，通過與二態系統測試點選取結果進行對比分析，證明了所提出的方法在系統故障與退化狀態測試性分析方面的有效性。