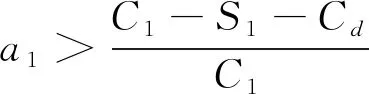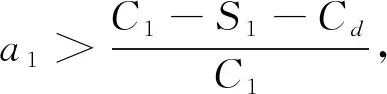政府補貼下建筑廢棄物資源化的演化博弈分析
李進濤, 吳 騫
(湖北工業大學土木建筑與環境學院, 湖北 武漢 430068)
隨著我國城市化的快速發展,建筑行業發展迅猛,同時也產生了大量的建筑廢棄物。據統計,我國建筑廢棄物總量約占城市固體廢棄物總量的30%~40%[1]。我國建筑廢棄物的處理方式主要是填埋和露天堆放,這不僅造成環境污染,而且還浪費資源。建筑廢棄物資源化利用可以降低對天然材料的依賴從而有效節約資源、減少污染、刺激經濟,是建筑廢棄物產生后最有效的處理方式[2]。
在過去的幾十年里,研究者從不同的視角對建筑廢棄物資源化問題進行了研究。在資源化管理手段方面,有學者指出政策支持對鼓勵采取減廢措施很重要[3],如實施建筑廢棄物處置收費政策[4],實施獎懲相結合的政策[5],將PPP模式引入建筑廢棄物處理產業[6],這些均能有效解決建筑廢棄物的管理問題。還有些學者對建筑廢棄物資源化的效果進行評估。例如,評估建筑廢棄物管理以及不同處置方法的經濟和環境效益[7-8]、不同分類系統對環境效益的影響[9]、建筑廢棄物移動式資源化處置的環境影響[10]。另外,許多學者還探究了建筑廢棄物管理的影響因素,如Osmani和朱姣蘭等研究了從業人員建筑廢棄物管理行為的影響因素[11-12],Lu等識別出建筑廢棄物有效管理的七個關鍵成功因素[13],Hao等指出影響建筑廢棄物管理的因素包括法規的完善程度、政府的監管力度和回收市場的成熟度[14]。
上述研究主要關注建筑廢棄物資源化行業的外部結構,然而,研究資源化行為決策的內在機制是提高資源化率的重要途徑。隨著博弈論的發展,演化博弈為研究行為決策提供了一種實用的方法。近幾年有學者運用演化博弈來分析建筑廢棄物資源化行業利益相關者的行為決策。例如,分析有無公眾參與下建筑承包商和政府部門的決策行為[15],研究政府部門與建筑垃圾生產單位之間的策略選擇[1],探究不同社會監督水平下施工單位與監管部門的演化策略[16]。前人的研究主要集中在政府和單個利益相關者之間的行為決策的影響,忽略了建筑廢棄物資源化過程中兩個主要的參與主體,即建筑企業和建筑材料制造商之間的合作以及政府干涉對雙方合作的影響。鑒于此,本文構建建筑企業與建筑材料制造商之間的博弈模型,探究建筑企業和建筑材料制造商的策略選擇,分析在政府補貼下,雙方決策行為的演化路徑以及政府補貼的合理范圍。為了便于分析,本文將廢棄物資源化利用企業和建材生產企業抽象為建筑材料制造商。
1 演化博弈模型的構建
對于建筑企業,面臨兩種策略選擇:一是將建筑廢物運送至建筑材料制造商作為原材料進行資源化,但此時會產生額外的分類分揀成本;二是直接將建筑廢棄物運送至填埋場。對于建筑材料制造商,也面臨著兩種策略選擇:一是選擇建筑廢棄物作為原材料,對其進行分類、處理,并在工廠中用于生產建筑材料,但此時需要引入先進的設備、技術和人員,因此需要投入額外的成本;二是選擇天然原料作為原材料來生產建筑材料。綜上所述,建筑企業和建筑材料制造商的策略集合為(參與,不參與)。
基于上述策略,本文做出下列假設:
假設一:博弈雙方均為有限理性,他們都能夠學習和適應動態環境變化,并在建筑廢棄物資源化過程中調整和優化策略。
假設二:當博弈雙方選擇參與資源化時,建筑廢棄物資源化行業運行良好,并帶來一定的環境、社會和經濟效益F。建筑企業和建筑材料制造商可從F中獲得的利益比例分別為α和β。當只有一個或兩個利益相關者都不參與資源化時,就不會產生環境、社會和經濟效益。
假設三:如果建筑企業選擇參與資源化,則額外的分類分揀成本為C1,此時還會得到政府的成本補貼,補貼率為a1。若建筑材料制造商不參與資源化,那么建筑企業的收益為S1;若建筑材料制造商參與資源化,那么建筑企業的收益為S1+αF。相反地,如果建筑企業不參與資源化而將廢棄物運至填埋場填埋,則填埋成本為Cd。
假設四:如果建筑材料制造商不參與資源化,則其收益為S2,運營成本為C2。相反地,如果建筑材料制造商參與資源化,且建筑企業也參與資源化,則其收益為S2+βF,但是建筑材料制造商還需要承擔引入先進設備、技術和人員所花費的額外成本C3,但此時會得到政府的成本補貼,補貼率為a2。
假設五:選擇參與資源化的建筑企業比例為x,選擇不參與資源化的建筑企業比例為1-x。選擇參與資源化的建筑材料制造商的比例為y,選擇不參與資源化的建筑材料制造商的比例為1-y,顯然,0 ≤x≤ 1,0 ≤y≤1。
基于上述模型描述與假設,建立了政府補貼下建筑企業和建筑材料制造商之間的收益矩陣,如表1所示。

表1 建筑企業和建筑材料制造商之間的收益矩陣
2 演化博弈模型分析
2.1 復制者動態方程求解
根據表1,可得出建筑企業參與資源化時的期望收益E11,不參與資源化時的期望收益E12以及平均收益E1。計算式如下:
E11=y[S1+αF-(1-a1)C1]+(1-y)[S1-(1-a1)C1]
(1)
E12=y(-Cd)+(1-y)(-Cd)=-Cd
(2)
E1=xE11+(1-x)E12
(3)
根據Malthusian動態方程,由式(1),(2),(3)可得建筑企業參與資源化比例下的復制動態方程:
(4)
同理,建筑材料制造商參與資源化比例下的復制動態方程為:
(5)
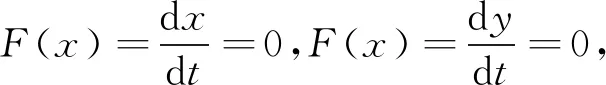
2.2 演化穩定策略分析
利用復制動態方程求出的局部均衡點不一定就是系統的演化穩定策略(ESS),根據Friedman法,可以通過系統的雅可比矩陣J的局部穩定分析得出系統的演化穩定策略。
只有當矩陣J滿足以下兩個條件:1)矩陣的行列式大于零(即DetJ>0);2)矩陣的跡小于零(即TrJ<0)時,該點具有局部穩定性,即為穩定演化策略。
根據方程(4)和(5),可得該系統的雅可比矩陣為:
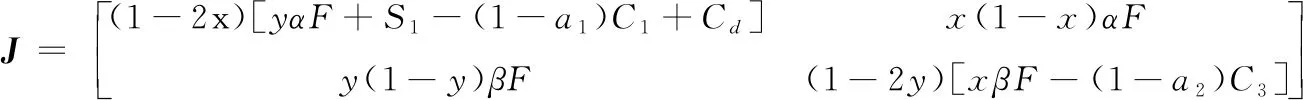
將前面5個均衡點代入到上述矩陣,可求得該系統的DetJ和TrJ如表2所示。
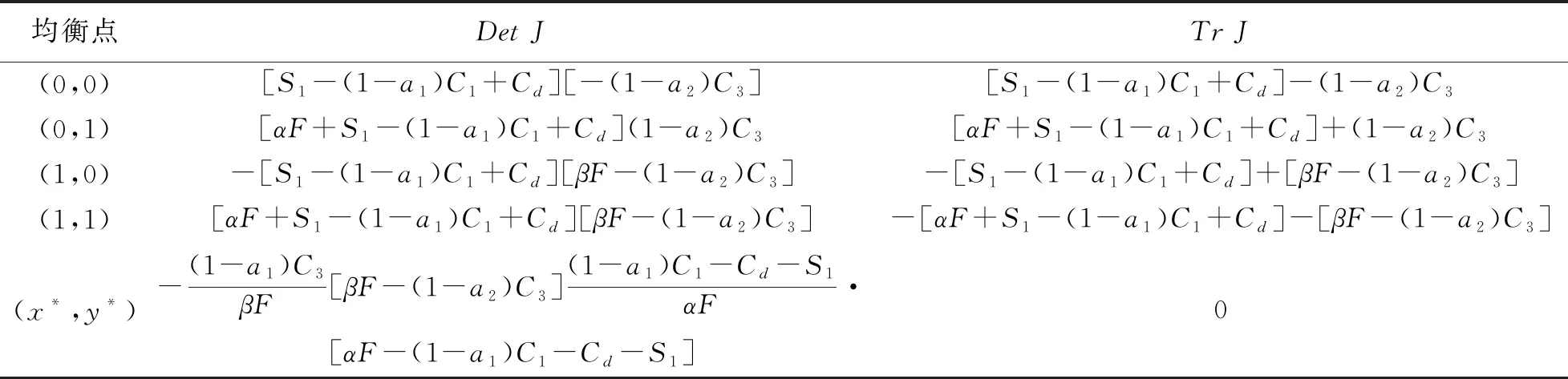
表2 系統均衡點對應的Det J和Tr J
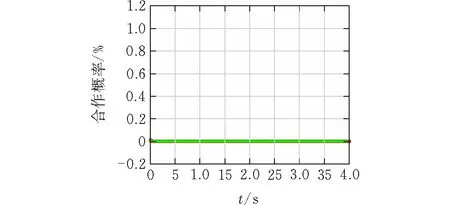
情形一:當S1-(1-a1)C1+Cd<0且αF+S1-(1-a1)C1+Cd<0時,系統相位演化圖如圖1a和b所示。此時(不參與,不參與)是雙方的最終選擇。對于建筑企業來說,加上增量收益αF后的凈收益小于填埋的凈收益,此時建筑企業傾向于不參與資源化;而對于建筑材料制造商來說,由于建筑企業不愿意參與資源化而將產生的建筑廢棄物直接運送至填埋場填埋,使得建筑材料制造商缺乏原材料來源,因此無論增量收益βF是否大于政府補貼后的額外成本,此時參與資源化的建筑材料制造商的比例將減少,最終雙方無法達成合作的局面。
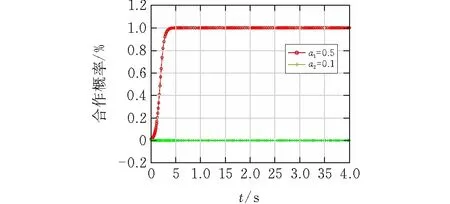
情形二:當S1-(1-a1)C1+Cd>0且βF>(1-a2)C3時,系統相位演化圖如圖1c所示。此時(參與,參與)是雙方的最終選擇。此時,建筑企業參與資源化帶來凈收益大于填埋的凈收益,建筑材料制造商資源化帶來的增量收益βF大于政府補貼后的額外成本,雙方均有利可圖,所以雙方均愿意參與資源化。
情形三: 當S1-(1-a1)C1+Cd>0且βF<(1-a2)C3時,系統相位演化圖如圖1d所示。此時(參與,不參與)是雙方的最終選擇。此時,建筑企業參與資源化帶來的凈收益大于填埋的凈收益,建筑材料制造商資源化帶來的增量收益βF小于政府補貼后的額外成本。所以建筑企業愿意參與資源化,而建筑材料制造商不愿意參與資源化,最后雙方無法達成合作。
情形四:當S1-(1-a1)C1+Cd<0,αF+S1-(1-a1)C1+Cd>0且βF<(1-a2)C3時,系統相位演化圖如圖1e所示。此時(不參與,不參與)是雙方的最終選擇。對于建筑企業來說,參與資源化后的凈收益大于填埋時的凈收益,所以建筑企業傾向于參與資源化;對于建筑材料制造商來說,增量收益βF小于政府補貼后的額外成本,所以建筑材料制造商不愿意參與資源化。由于建筑材料制造商不參與資源化,那么建筑企業將被迫無法進行資源化,最后雙方無法達成合作。
情形五:當S1-(1-a1)C1+Cd<0,αF+S1-(1-a1)C1+Cd>0且βF>(1-a2)C3時,系統相位演化圖如圖1f所示。對于建筑企業來說,參與資源化的凈收益小于填埋的凈收益,但加上增量收益αF后的凈收益大于填埋的凈收益,所以建筑企業傾向于參與資源化;對于建筑材料制造商來說,增量收益βF大于政府補貼后的額外成本,所以建筑材料制造商也愿意參與資源化。但只要有一方不參與資源化,最終將無法達成合作局面。所以,系統的ESS為(0,0)和(1,1)。
2)相關性關聯關系,相關性關聯是指同一視圖或者不同視圖檔案特征之間存在的依存、制約、因果等隱含的關系。構建相關性關聯關系是指通過分析已有的檔案相關關系,基于統計分析尋找檔案特征同時出現的規律和模式的過程。兩個特征之間的相關關聯分析多采用熵與互信息進行度量。對于任意的 f1,f2∈R,I表示(f1,f2)的互信息即I(f1,f2)=,給定閾值δ,當I(f1,f2)>δ時,認為特征fi,fj之間存在相關關系,即節點vi,vj之間存在相關關聯關系。
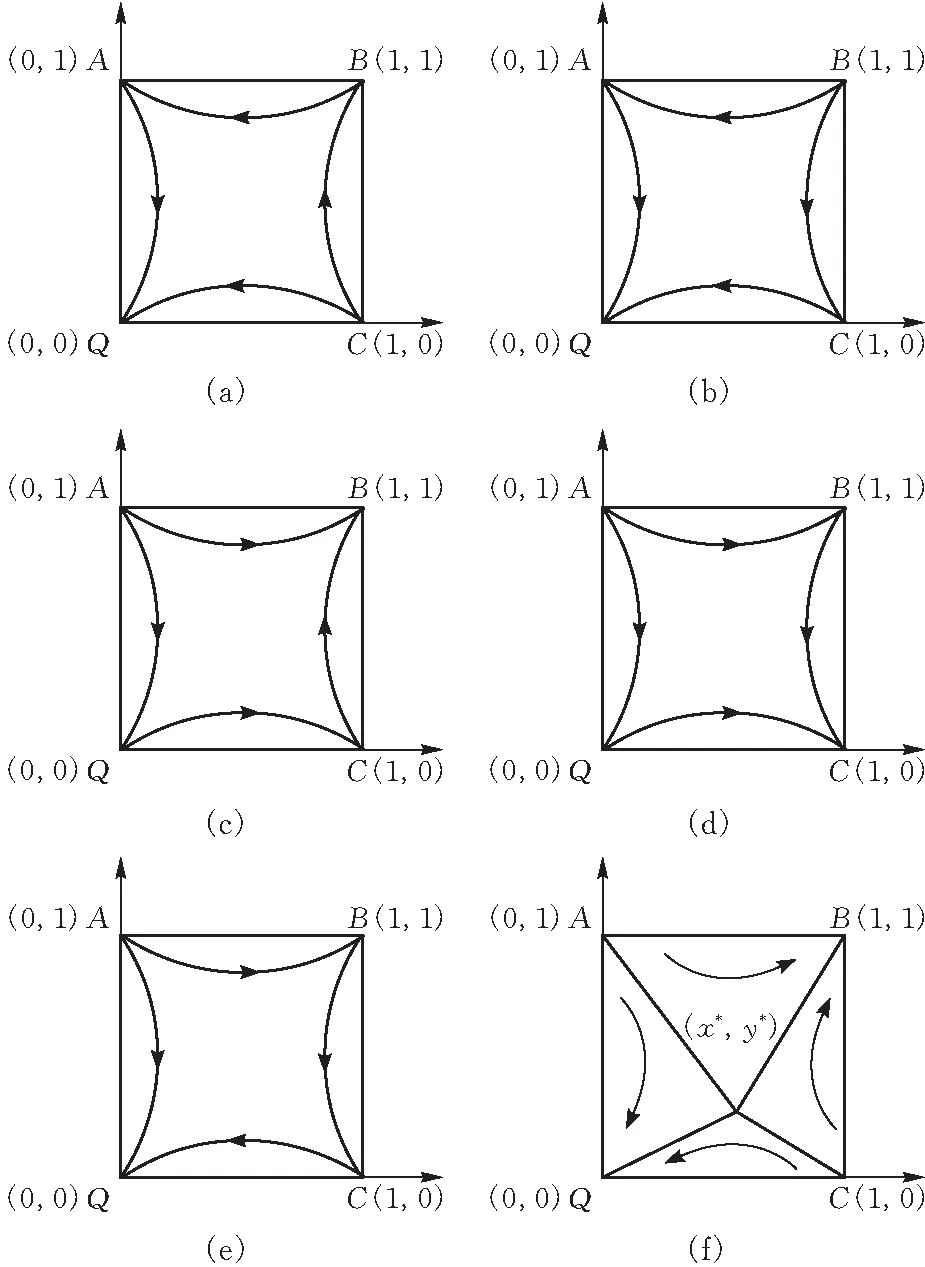
圖 1 系統演化相位圖
2.3 參數變化的影響
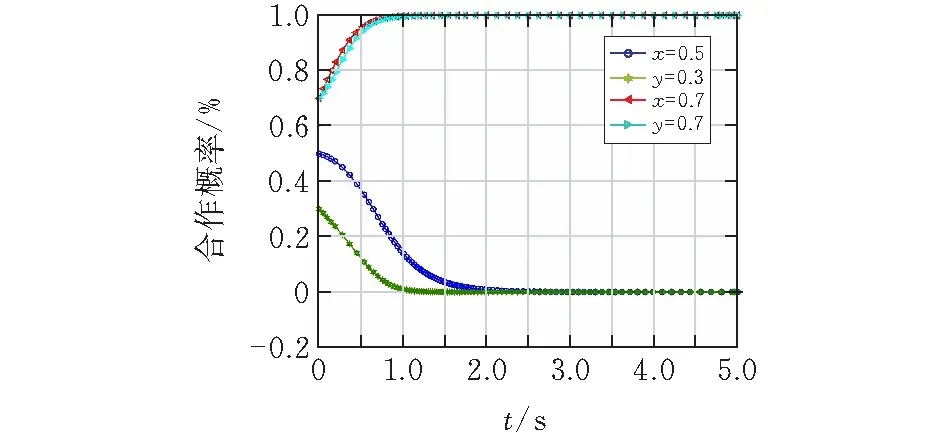
由前面的分析可知,當滿足S1-(1-a1)C1+Cd<0,αF+S1-(1-a1)C1+Cd>0且βF>(1-a2)C3時,系統的ESS為(不參與,不參與)和(參與,參與)。由于SOADC和SABCD的面積表示雙方是否合作的概率,所以這兩個區域的面積大小決定了系統最終演化結果。若SOADC>SABCD,演化結果趨向于(0,0);若SOADC 由圖1f可得SABCD的面積,即(1,1)為演化穩定策略的概率為: (6) 根據方程(6),影響系統演化的因素有9個,可以得出進一步的結論,如表3所示。 表3 因素變化對系統演化結果的影響 由表3可得:分類分揀成本為C1、引入先進設備、技術和人員所花費的額外成本C3越高,雙方合作的概率減小。建筑企業和建筑材料制造商只要有一方成本過高,雙方合作的概率將減小。此時,政府補貼對促進雙方合作具有重要意義,當補貼率a1、a2越大,雙方合作的概率也將增大。 填埋成本為Cd,資源化效益F,兩個利益相關者從F中獲得的利益比例α和β,建筑企業的收益S1越大,雙方參與資源化的概率越大。對于建筑企業,參與資源化的收益越大、填埋成本越高,建筑企業越傾向于參與資源化,隨著建筑企業資源化的比例增加,建筑材料制造商實施資源化的比例也將增加,最終雙方達成合作。當資源化帶來的效益F越大且雙方從F中獲得的利益比例α和β越大,雙方參與資源化的概率也越大。 為了更直觀的研究建筑企業和建筑材料制造商之間的演化策略,本節利用MATLAB來模擬參數變化時相應演化博弈策略變化的結果。考慮到篇幅限制以及相關參數的數據獲取困難,本文具體參數值的設置滿足前述的基本假設。 為了檢驗情形五中建筑企業和建筑材料制造商是如何在策略(不參與,不參與)和策略(參與,參與)之間進行權衡,此時參數應滿足S1-(1-a1)C1+Cd<0,αF+S1-(1-a1)C1+Cd>0且βF>(1-a2)C3。所以,令S1=20,a1=0.2,a2=0.4,C1=35,Cd=5,C3=15,α=0.3,β=0.5,F=30。通過上述參數設置,可計算得x*=0.6,y*=0.33。固定其他參數,通過改變初始策略(x0,y0)來檢驗演化趨勢。由于x*=0.6,y*=0.33,因此,設初始策略(x0,y0)為(0.5,0.3)和(0.7,0.7)。演化趨勢如圖2所示。 由圖2可知,當x0=0.5 圖 2 情形五的演化趨勢 圖 3 a1=0,a2=0.1/0.2;a1=0.2,a2=0.1時雙方演化趨勢圖 圖 4 a1=0.5,a2=0.1時雙方演化趨勢圖 圖 5 a1=0.5,0.6,0.7和a2=0.2,0.3,0.4時雙方演化趨勢圖
3 演化博弈模擬仿真
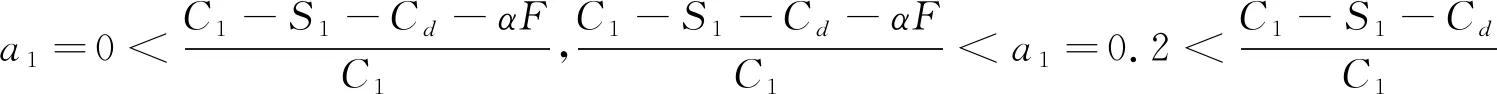
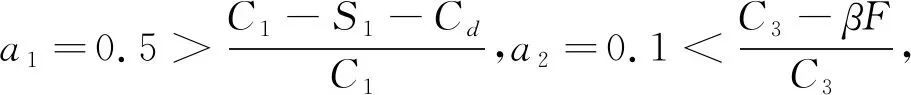

4 結論與建議