基于支持向量回歸與LSTM的城市PM2.5預測

尹博文，張亞娟，王曉芳，張素琪

（1.河北工業大學 人工智能與數據科學學院，天津 300401；2.天津商業大學 信息工程學院，天津 300134）

0 引言

城市PM2.5濃度反映地區的空氣污染程度，其含義是某地區空氣中細顆粒物含量，影響其變化的因素主要包括風速、濕度及NO2、SO2濃度等。2012年，中國開始按照新的《環境空氣質量標準》開展PM2.5監測并發布數據。通過科學的手段對PM2.5值進行準確預測可以指導人們生產生活，更能提醒環保部門及時進行污染防治[1]。

2009 年Wang 等[2]通過自回歸綜合移動平均值（ARIMA）線性模型方法對洛杉磯市PM2.5進行了有效預測；2010年陳俏等[3]將支持向量回歸與其他機器學習方法進行對比，說明了支持向量回歸（SVR）在城市PM2.5預測中的優勢，同時通過對簡單核函數以及模型參數分析，得出不同核函數和參數直接影響預測準確度的結論；2012年Yao等[4]利用人工神經網絡進行了多源PM2.5的估計，結果表明該方法較多元回歸方法顯著提高了預測準確度，但是在PM2.5值較高時，預測誤差出現明顯的上升；2013年白鶴鳴等[5]利用BP神經網絡有效預測北京市區空氣污染指數，但是該模型呈現出訓練時間相對較長、結構較為簡單難以應對復雜變化等問題。2015年Zou等[6]利用粒子群算法優化的SVR對儀器故障進行了回歸預測，較優化前模型獲得了更好的結果；2016年遲恩楠等[7]利用小波和乘法混合核函數的支持向量回歸方法成功的對空間風壓進行了預測；同年Zhu等[8]將ARMA時間序列與BP神經網絡相結合，得到了更好的PM2.5預測結果，較使用單一方法進行預測提高了預測準確度，但是實驗中仍缺少與其他方法的結果對比。2017 年Ye 等[9]利用ARIMASVR的方法對股票價格進行了較為準確的預測，該結果證明了將時間序列作為研究目標的方法可以顯著降低原本模型的預測誤差；2019年Song等[10]提出一種基于長短期記憶和卡爾曼濾波的預測模型，其結果較使用單一的LSTM提高了對空氣中污染氣體的預測準確率。

為了建立更加準確的城市PM2.5濃度預測模型，提出一種將支持向量回歸與長短期記憶相結合的方法。首先使用Morlet小波核函數代替傳統支持向量回歸中應用較多的徑向基核函數（RBF），解決了RBF非完全正交基的問題；然后使用改進的粒子群算法對該Morlet核函數進行參數優化，不但極大程度避免了算法陷入局部最優解，同時可在良好的時間復雜度內獲得更優的預測結果；最后考慮到時間序列對城市PM2.5濃度的影響，將包含時間序列的LSTM預測結果與SVR預測結果進行非線性疊加，得到最終的預測結果。在實驗部分進行了多組對比，結果均較ARMA時間序列、SVR與LSTM等較大地提高了預測準確度。

1 改進粒子群算法優化的小波支持向量回歸

1.1 支持向量回歸原理

支持向量回歸[11-12]是由支持向量機的概念發展而來，用于非線性條件下的預測等多種場景。支持向量回歸問題可以描述為尋求非線性空間的映射關系表示如式（1）所示：

式中：xi表示的是訓練集中各維度的值；i表示各維度變量；ω表示變量系數；b表示偏置量。

對于樣本中的(x,y)，所求得到一個預測模型f使得預測結果與真實值最為接近。假設該回歸模型幾乎可以完全表達真實值，只存在可以忽略不計的誤差ε，SVR問題可以轉化成式（2）：

式中：C為正則化常數；?ε為不敏感損失函數，?ε的表達式如式（3）所示：

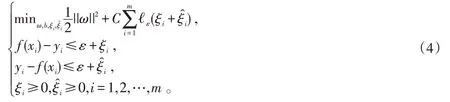
將式（5）代入到原式中，并且該過程需要滿足Karush-Kuhn-Tucker（KKT）條件，即需要滿足如式（6）所示：

支持向量回歸的解的形式，可以表示為如式（7）所示。

1.2 Morlet 小波核函數

支持向量回歸中核函數的作用是將低維線性不可分的情況映射到高維使之線性可分，此時引入合適的核函數如式（8）所示。

支持向量回歸的核函數一般選擇高斯核函數，然而高斯核函數并非完全正交基，考慮到小波函數可以通過伸縮以及平移的手段建立完全正交基，使SVR模型泛化能力更強[13-14]。小波函數可以作為支持向量回歸核函數的條件是該基函數滿足Mercer定理，構造支持向量回歸的核函數的平移不變小波核函數形式，如式（9）所示：

該平移不變小波核函數需要滿足傅里葉變換公式，如式（10）所示：

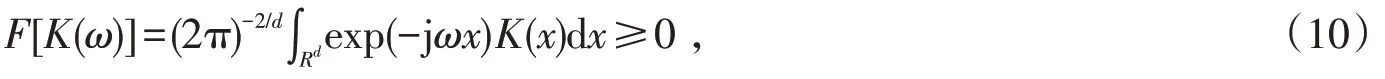
式中：Rd代表的是x的取值范圍；d維的實數空間。

Morlet小波函數的實數表達如式（11）所示：

滿足上述條件的實驗所應用到Morlet小波核函數如式（12）所示：

式中：m表示空間維度；ai表示伸縮因子。

1.3 改進粒子群算法參數優化

支持向量回歸核函數中存在未知參數，分別是懲罰因子C與參數sigma，未知參數的取值直接影響模型泛化效果[15]。通常解決最優值搜索問題可以采用的方法有遺傳算法、粒子群算法、蟻群算法等。考慮到粒子群算法模型簡單、收斂性能好、搜索效率高等優勢，同時需要盡量避免算法搜索過程陷入局部最優解，提出了改進粒子群算法對模型核函數參數進行最優值搜索。方法中粒子速度與位移更新公式如式（13）所示。

式中：vi(k)表示k時刻時的粒子的速度；xi表示粒子的位置；r1,r2分別為隨機均勻概率值，并且取值范圍是[0，1]；c1,c2表示學習因子；pbesti表示局部最優位置；gbesti表示全局最優位置。式中存在未確定的參數W，表示粒子移動的慣性系數，具體意義是當該值較大時，該粒子將在原方向上有較大的移動能力，當值較小時，粒子在周圍方向具有較高的搜索能力。該值一般采用線性函數取值如式（14）所示，也因此造成了局部最優解的情況。為了盡可能地避免粒子群算法由此產生的性能問題，同時保證搜索算法較低的時間復雜度，W值的選取采用非線性自適應算法，如式（15）所示：

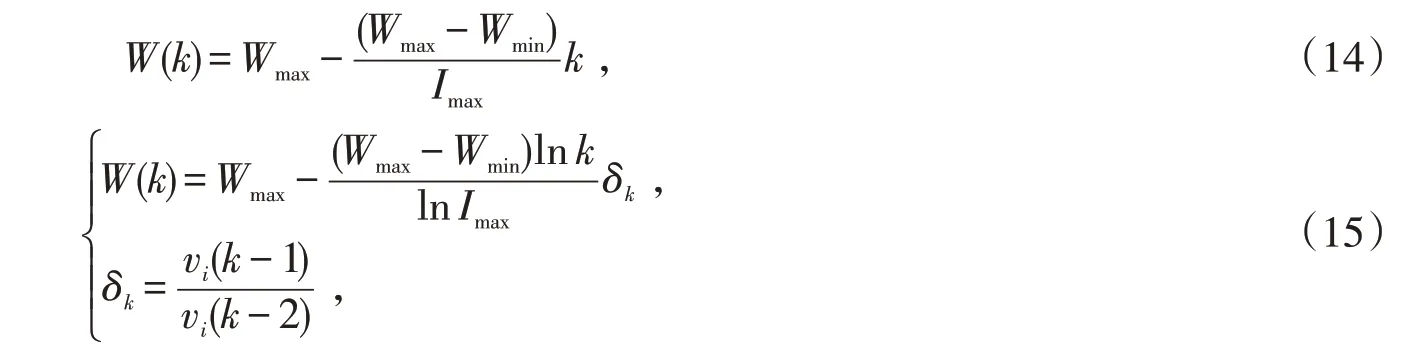
式中：Wmax與Wmin分別表示實驗預先設定的最大及最小的慣性系數；Imax表示最大的迭代次數；k表示已迭代次數；引入一個概念值δk，表示速度趨向基數，該值依賴于之前兩個時刻的速度變化比例。該值的不斷變化，實現了W的自適應變化。這里值是非線性的，降低了線性函數情況下陷入局部最優解的可能。改進粒子群算法應用到Morlet-SVR的參數優化中，具體流程如算法1所示。

算法1 改進粒子群算法參數優化

輸入 實驗訓練集數據，Morlet核函數表達式，粒子群最大進化次數，調優參數精度范圍accuracy，粒子慣性公式，粒子群最大速度，粒子種群數量

輸出Morlet核函數的最優參數sigma 與支持向量回歸最佳參數C

2 基于支持向量回歸與LSTM 的預測模型

2.1 LSTM 原理

長短期記憶網絡（LSTM）是一種改進后的循環神經網絡，通過設置隱藏層間的相關權重，解決RNN無法處理長距離依賴的問題[16-18]，在諸多時間序列預測的場景下廣泛應用。PM2.5這一與時間密切相關的復雜變量需要融合時間序列進行分析，從而提高預測的準確性。在LSTM中包含三個重要的門：更新門、遺忘門、輸出門，其模型圖如圖1所示。

圖1 LSTM 模型示意圖Fig.1 Schematic diagram of LSTM model

LSTM單元的方程組如式（16）所示：

式中：ft其中是關于遺忘門的遺忘閾值；ot表示輸出門的輸出閾值；ht表示當前細胞輸出。在更新門ut（圖中Update）中存在參數權重Wu與偏差bu，其作用是確定sigmoid激活函數更新細胞單元的時機，當sigmoid函數取值接近1時，將更新該單元，接近0則忽略。表示部分輸出tanh，影響該值變化的因素包括權重WC與偏差bC；Ct-1表示t-1時刻的細胞狀態，以及ut共同影響最終的結果Ct。

2.2 支持向量回歸與LSTM 結合模型

支持向量回歸方法在解決有限規模樣本、非線性等問題體現出良好的性能，較深度學習方法預測更迅速，經驗風險更小；LSTM能夠發掘時間序列對PM2.5的影響。考慮到2種方法在不同場景下的優勢，文章的研究目標需要同時考慮預測性能、經驗風險等，將上述2種方法的預測結果按照表達式（17）所示，構成最終的預測結果。

式中：y1i、y2i分別表示SVR、LSTM這2種方法在第i次實驗中的預測結果；xi表示一維向量；φ與φ表示不同的函數。根據式（18）所示進行結果計算，得到最終的預測結果，式中：α表示時間關聯系數，該值的取值范圍是[0，1]，與預測的時間間隔正相關，間隔越久該值的取值越大；M表示|y1i-y2i|的最大值。

基于支持向量回歸與LSTM 的城市PM2.5預測模型圖如圖2所示。

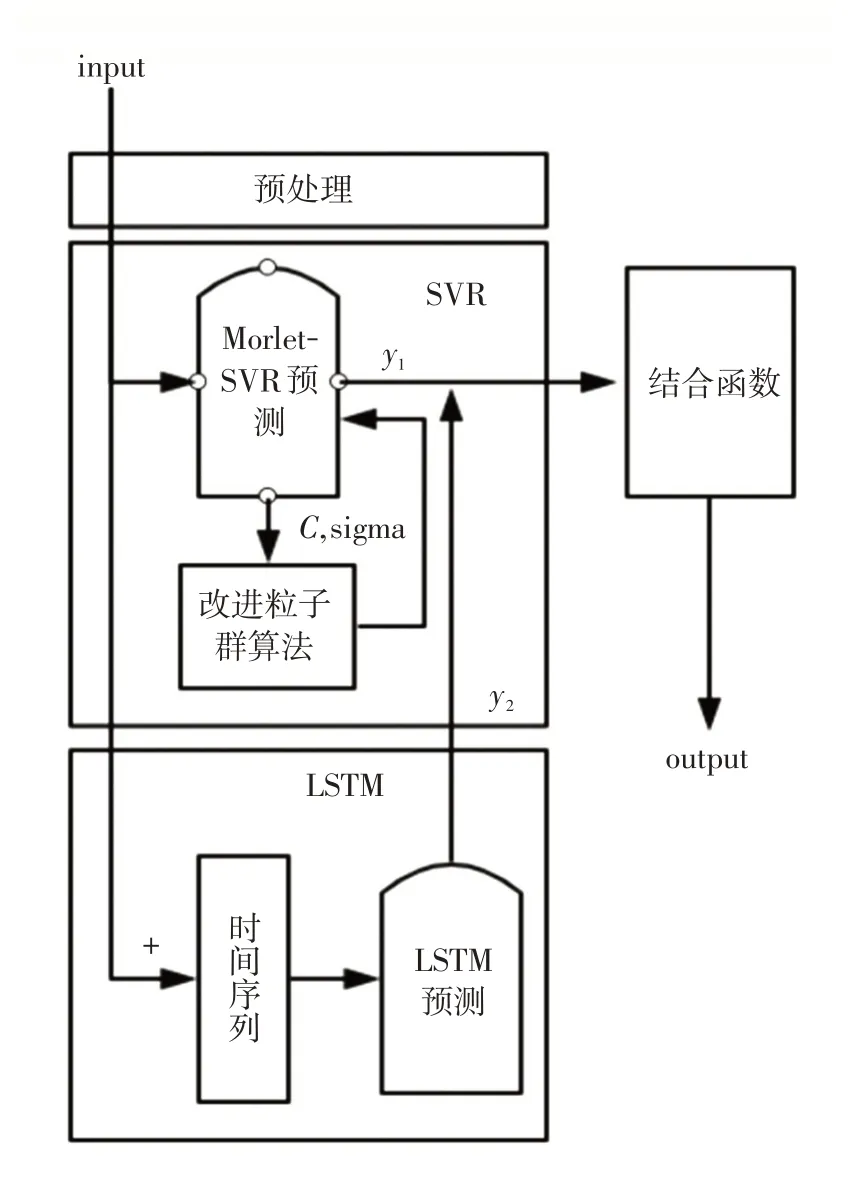
圖2 基于支持向量回歸與LSTM 的預測模型圖Fig.2 Prediction model graph based on support vector regression and LSTM

3 實驗與結果分析

在實驗預處理方面，采用KNN-Kmeans 的方法進行不完全數據集的填充；采取分別歸一化的方式處理訓練集與預測集數據，實驗過程的流程如圖3 所示。在結果分析中首先分別對比ARMA、隨機森林、神經網絡以及支持向量回歸方法預測結果；然后對比Morlet小波核函數以及RBF核函數支持向量回歸的預測結果；接下來通過改進粒子慣性函數的方式應用粒子群算法對Morlet 核函數中的參數進行尋優，并將尋優前后的結果進行對比；最后針對城市PM2.5這一與時間序列密切相關的研究變量，將支持向量回歸結果與LSTM 結果進行非線性疊加計算，將最終預測結果與其他方法的結果進行對比。

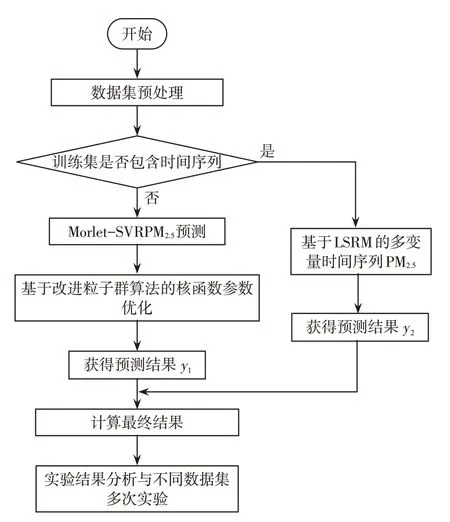
圖3 實驗過程流程圖Fig.3 Flow chart of experiment process

3.1 支持向量回歸與LSTM 結合模型

實驗中所用到的數據，均來源于某市3 處監測點的真實觀測數據。首先選取連續的720 h 的氣象數據（濕度、風速、氣壓）與環境污染數據（PM2.5、PM10、SO2、NO2），并按照前648個作為實驗訓練集，剩余后72個作為測試集進行劃分。由于選取的列數據中出現少量數據缺失，采用KNN-Kmeans方法進行數據填充，綜合了2種聚類方法實現了更符合本數據集原始特征的填充方法：選定時間間隔為5 h，當時間間隔內的數據超過半數，即3 個或3 個以上為某一值時，認為在該時間間隔內的大氣狀況相對穩定不變，此時實驗將該值作為填充值；若不存在上述情況，則按照K均值的計算方法進行填充，選擇時間間隔內所有數據的平均值進行填充。實驗數據填充中的時間間隔根據實驗需要和原始數據集的特征設定。

為獲得量綱統一的數據集，避免由于個別因素的比例尺過大帶來的實驗預測影響，同時提升模型的收斂速度和運算精度，采用對訓練集和預測集分別歸一化處理的方法，排除了因數據集隨機劃分造成的誤差，歸一化公式如式（19）所示，結果表示歸一化后的向量：

SVR訓練平臺為WINDOWS 10操作系統，8 G內存，2.7 GHz CPU環境并應用libSVM程序庫進行Matlab 編程。在粒子群優化實驗前根據實驗需要，預先設置種群的最大進化數量maxgen 及初始數量sizepop取值分別為15和1 000；設置最大最小變化結果值，使所求參量在可控范圍內變化，防止產生過高的時間冗余。將popCmax 的初始值設為1 000，表示SVR 模型參數C的變化的最大值，popCmin 的初始設為0.05；popsigmamax 的初始為1 000，表示SVR參數sigma 變化的最大值，popsigmamin 設置為0.01；設置粒子的初始速度VC與Vsigma均為5。

LSTM 預測部分利用tensorflow 機器學習訓練平臺，選取的數據集包括時間序列以及預處理后的數據集；設置輸入維度input_size 數值為7，輸出維度output_size 為1，隱藏層單元rnn_unit 數值10，以及學習率lr為1，時間步time_step 的值為12，每批訓練樣本數batch_size 數值40，重復訓練次數numbers 數值5 000。

3.2 支持向量回歸與LSTM 結合模型

3.2.1 監測點PM2.5 基本情況與算法分析

實驗中對研究的3 個國控監測點的720 個PM2.5的值進行了初步分析，通過直觀觀察可以方便建立數學模型。各個監測點的PM2.5值數據變化均較為明顯，呈現出非線性變化規律，不同時間間隔的極值不同，平均PM2.5水平在90 μg/cm3；3個監測點PM2.5反映出的圖形較為相似，其污染與氣象差異相對較小，如圖4所式。針對圖像呈現的復雜變化規律，支持向量回歸恰能夠在小規模樣本數據下體現其良好的自適應性。均方誤差MSE 是評價預測模型的重要指標，客觀反映了預測模型的誤差大小，誤差越小預測準確度越高；最大誤差是預測值與實際值之差的絕對值最大值，反映了極端個體與真實值的偏離程度。表1為對比不同機器學習方法的均方誤差與最大誤差，SVR體現了一定的優勢。

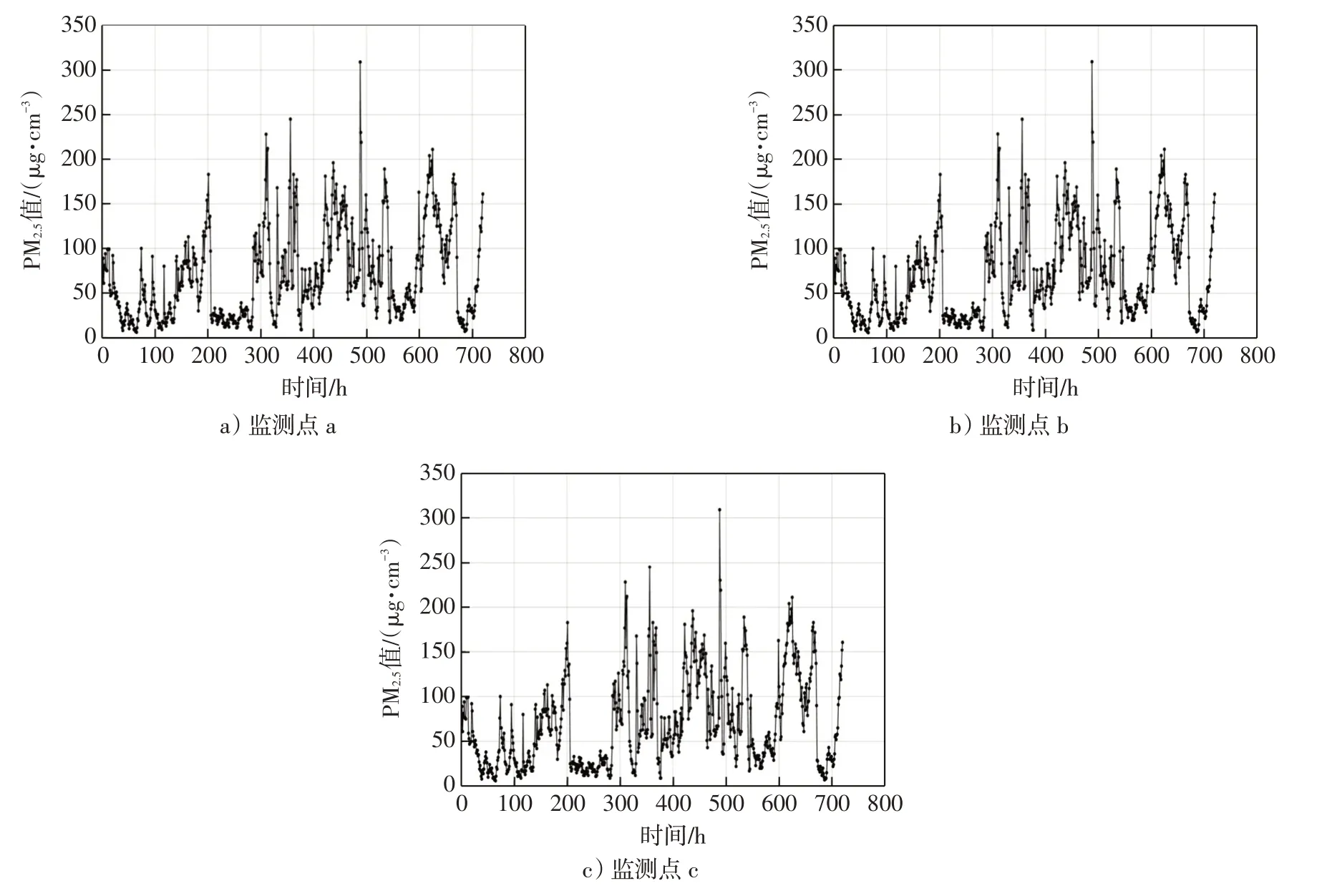
圖4 監測點PM2.5隨時間變化Fig.4 Monitoring point PM2.5 changes with time

表1 不同方法預測結果對比Tab.1 Error comparison of prediction results under different methods

3.2.2 Morlet 小波核SVR 預測結果

分別使用Morlet 小波核與RBF核支持向量回歸進行建模，并與預測集真實值的數值進行對比結果如圖5所示。

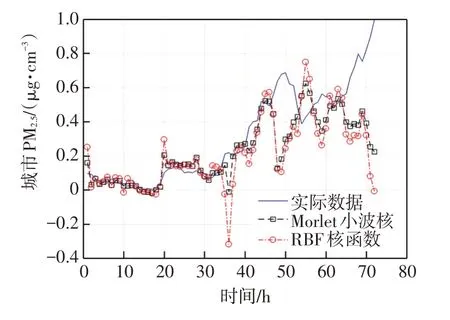
圖5 Morlet 小波核與RBF 核SVR 預測結果對比Fig.5 Comparison of SVR prediction results between Morlet wavelet kernel and RBF kernel

表2所示對比不同核函數SVR的模型預測均方誤差、最大誤差。由此得出實驗結論：Morlet 小波核SVR 在城市PM2.5預測建模上較其他核函數精度更高，體現了該應用的合理有效性。

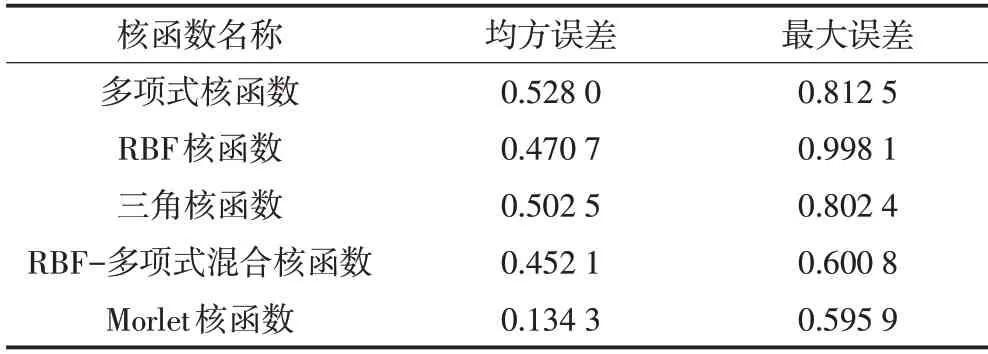
表2 不同核函數預測結果對比Tab.2 Comparison of prediction results of different kernel functions

3.2.3 改進粒子群算法參數優化結果與預測對比

改進的粒子群優化算法的目的是獲取模型最優參數C以及sigma，實驗結果如圖6所示獲得到了最優參數。

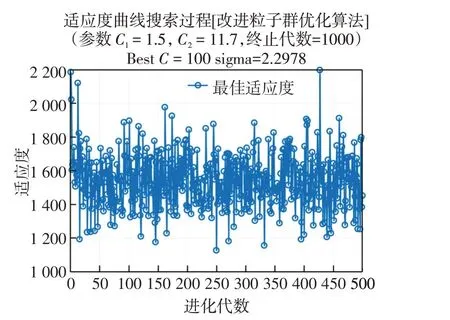
圖6 改進粒子群算法最優參數搜索結果Fig.6 Search results of optimal parameters of improved particle swarm optimization

根據搜索結果，確定了Morlet-SVR 最佳參數值，并均將參數代入實驗中，如圖7中顯示了參數優化前后預測結果與測試集實際值對比。

據圖7 分析，粒子群算法優化前當時間間隔為45 h，預測結果與實際結果開始出現明顯偏差，優化后則是在時間間隔大于55 h，出現小范圍偏差，大于65 h出現較大偏差。由此得出結論：改進粒子群算法可以提高準確預測的時間長度，能夠提高模型的預測精度。然而由于訓練數據集規模有限，且模型本身具有一定的局限性，當時間間隔較大時，預測結果依舊存在著與實際值的偏差。

3.2.4 基于SVR 與LSTM 的模型預測結果

基于多變量時間序列的LSTM 可以有效解決長距離依賴問題，同時發掘時間序列對PM2.5濃度變化的影響。如圖8所示為基于該方法的預測結果。

圖8中顯示預測數據在45～70 h基本與實際數據一致，較支持向量回歸方法不同，LSTM預測結果在0～45 h反映出與實際值的誤差。在20～30 h與40～45 h這2個時間段有較大偏差；同時LSTM預測時間較長，模型中參數較多，只利用該方法不能達到對實驗結果的預期。表3 所示為不同時間間隔2 種方法的均方誤差對比。

表3 不同時間間隔MSE 結果對比Tab.3 Comparison of MSE results in different time intervals

據圖7 和圖8 的結果分析，在預測結果時間段的后20%中LSTM 解決了支持向量回歸預測效果明顯下降的問題；然而SVR模型簡單，且在預測結果時間段的前50%中優勢明顯。最終將支持向量回歸與LSTM這2部分預測結果按照式（18）進行非線性疊加：當相距起始時間節點越近，基于改進粒子群算法的Morlet支持向量回歸預測結果更好，當時間間距較大，使用基于多變量時間序列的LSTM 效果更佳。2 種方法的預測結果偏差較大時，LSTM 更能反映實際值的變化趨勢，計算結果體現了自適應性。實驗結果對比基于PSO-SVR與LSTM-SVR這2種方法，如圖9所示。

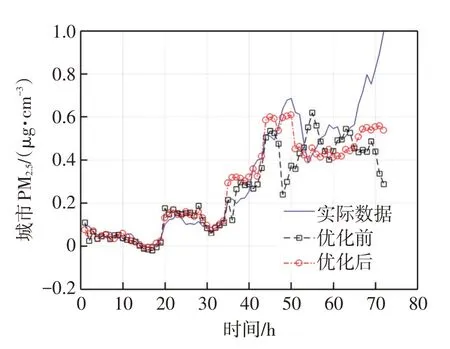
圖7 改進粒子群優化前后預測結果對比Fig.7 Comparison of prediction results before and after improved particle swarm optimization

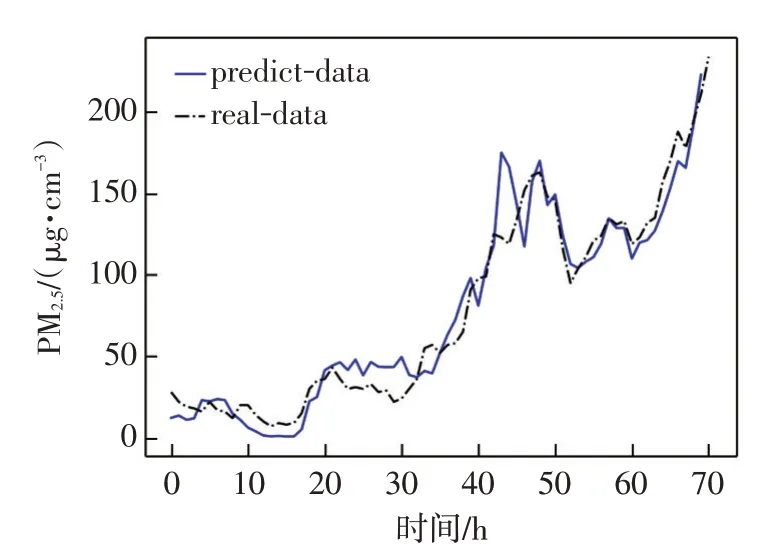
圖8 基于LSTM 的時間序列預測結果Fig.8 Prediction results of time series based on LSTM

從圖9 中可以觀察到，基于LSTM-SVR 的研究方法較使用改進粒子群優化的Morlet-SVR進一步提高了預測精度。通過相關損失函數平均絕對誤差MAE 以及模型準確率pre 作為衡量該模型預測準確度的指標。其中MAE 越小說明預測的準確度越高，計算公式如式（20）所示：

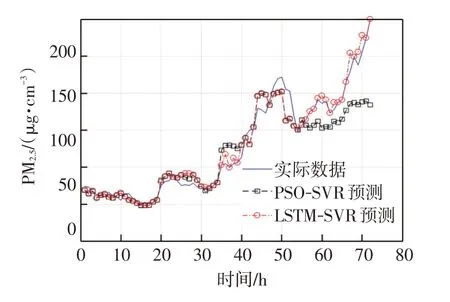
圖9 基于PSO-SVR 與LSTM-SVR 的結果對比Fig.9 Comparison of results based on PSO-SVR and LSTM-SVR

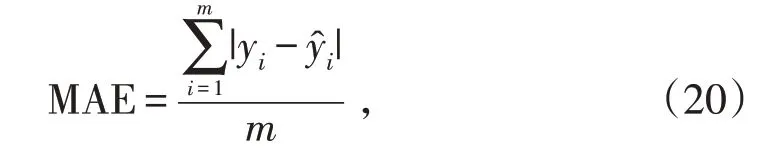
式中：m表示預測集合記錄數量；yi表示該條記錄的預測結果；表示該條記錄的真實結果。模型準確率pre 反映了預測值與實際值的相似程度，該值的計算方法滿足式（21）：

式中：θi表示單次準確預測值，可以取4個值，當預測結果與真實結果滿足不同的條件時，準確預測值也不同。其對應關系因實際需要而制定，在本實驗中滿足式（22）：

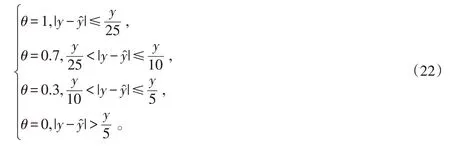
根據上述計算方法，獲得不同模型下的MAE 與pre值，如表4所示。

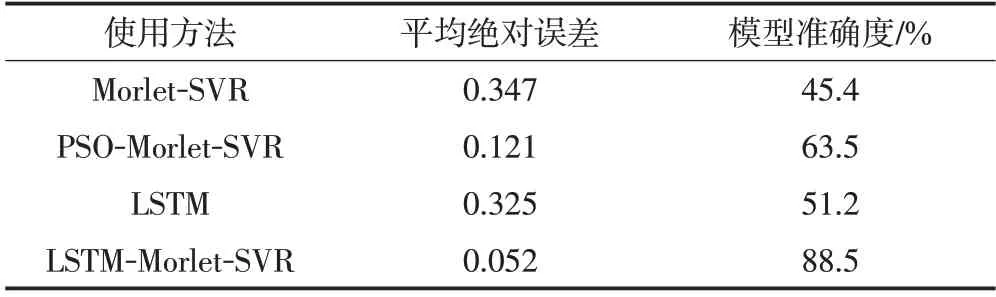
表4 不同模型準確度與誤差對比Tab.4 Comparison of accuracy and error of different models

最后利用不同方法對該市區3 處監測點進行預測結果準確度對比，結果如圖10所示。

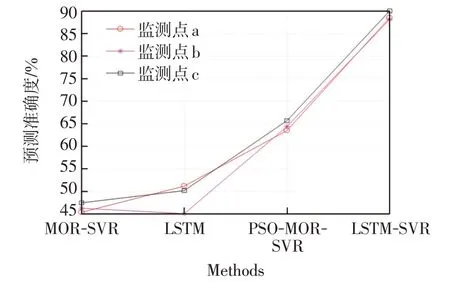
圖10 不同監測點基于不同方法的準確度結果對比Fig.10 Comparison of accuracy results of different monitoring points based on different methods

根據上述3 處監測點的預測結果顯示，基于支持向量回歸與LSTM相結合的方法均優于其他方法。

4 結語

文章提出了基于支持向量回歸與LSTM 的城市PM2.5預測模型。在模型建立的過程中，首先根據支持向量回歸方法以及Morlet 小波核的優勢，確定了支持向量回歸的核函數；為獲得更好的預測結果，采用改進粒子群算法對核函數的參數進行優化，并將最優參數代回模型進行預測；最后將非時間序列的Morlet-SVR 預測結果與時間序列下LSTM 預測結果進行非線性疊加，形成最終的預測結果，以滿足模型對時間序列依賴的需要。從各步驟的實驗結果可以看出，本文提出的基于支持向量回歸與LSTM的方法在城市PM2.5預測上較ARMA 時間序列、神經網絡、隨機森林等方法具有明顯優勢，同時較傳統的SVR與LSTM提高了預測準確度。后續工作將考慮對模型中的LSTM部分進行優化，通過合理設置隱藏層數、改變激活函數以及參數尋優等，進一步提高預測準確度。