Ergodic stationary distribution of a stochastic rumor propagation model with general incidence function

Yuhuai Zhang(張宇槐) and Jianjun Zhu(朱建軍)

College of Economics and Management,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China

Keywords: rumor propagation model,general incidence function,It?o’s formula,ergodic stationary distribution

1. Introduction

Recently,due to the pandemic of COVID-19,various rumors related to COVID-19 have been circulated on the internet. The rumors not only easily cause people’s emotional panic, but also cause other social problems. For example,“Novel coronavirus can be eliminated by using the blow dryer to blow the face and hands for a long time”, “Virus can be killed by drinking bleaching disinfectant” and other pseudoscience or malicious“conspiracy theory”. Although some authoritative media and experts have voiced against the rumors,there still are exponential forwarding and diffusion of rumors about the epidemic on social media,just like a virus with great replication ability, which urgently needs to respond with actions matching it. Thus, it is of great significance to study rumor propagation in online social networks for strengthening the supervision of network public opinion and purifying the cyberspace.

To minimize the harmfulness of rumors on online social network platforms as much as possible, it is necessary to understand the rules of rumor spreading on online social network platforms.In the past period of time,some mathematical models were established to investigate rumor spreading in the complex network.[10,13,23]In fact, the research of classical rumor spreading model started from 1960s. In 1964 and 1965,in order to compare the differences between the rumor spreading and virus spreading, Daley and Kendal[5,6]proposed the typical DK model of rumor spreading. In their model, they first divided people into three categories:ignorants(people who do not hear the rumor),spreaders(people who spread the rumor)and stiflers (people who know but do not spread the rumor).Since then,the original DK model had been modified and extended continuously, which made it possible to interpret the rumors in more detail. By changing the propagation mechanism, Maki and Thomson[26]further modified the DK model and established a new rumor propagation model-MT model.At the beginning of the 21st century, Zanette first extended the problems of rumor spreading to complex networks, who mainly investigated the rules of rumor propagation on a smallworld network and proposed an epidemic-like model.[34,35]Afterwards, some scholars devoted to studying some rumor propagation models in order to better control the rumors, see Refs. [8,18]. Recently, Tuwairqiet al.[1]proposed a rumor propagation model with incubation mechanism. In their work,some important results,such as the basic reproduction number of the model, the local stability and global asymptotic stability of the rumor-free and rumor equilibrium, were obtained under suitable conditions. Additional literature relating to the rumor propagation models in different patterns of groups,see Refs.[22,28,33]and the references therein.

To ensure these models can provide the realistic description of the rumor propagation, the incidence rate plays an important role. In 1927, Kermack and McKendrick[19]introduced the specific bilinear incidence rateβSIfor some disease spreading models. However, there were many problems when it was used in describing the disease spreading.To fit the phenomena of disease propagation, Capasso and Serio[4]proposed the saturated incidence rateβSI/(1+αI).After the works, many kinds of incidence rate in various biological models were considered by many scholars, see Refs.[2,9,17,24,25,30–32].From these literature,one can find that models with more general incidence can provide more complex dynamics than those with the bilinear or standard incidence rate.[3,20]Therefore, on social networks, one may consider the following deterministic rumor propagation model with general incidence function:

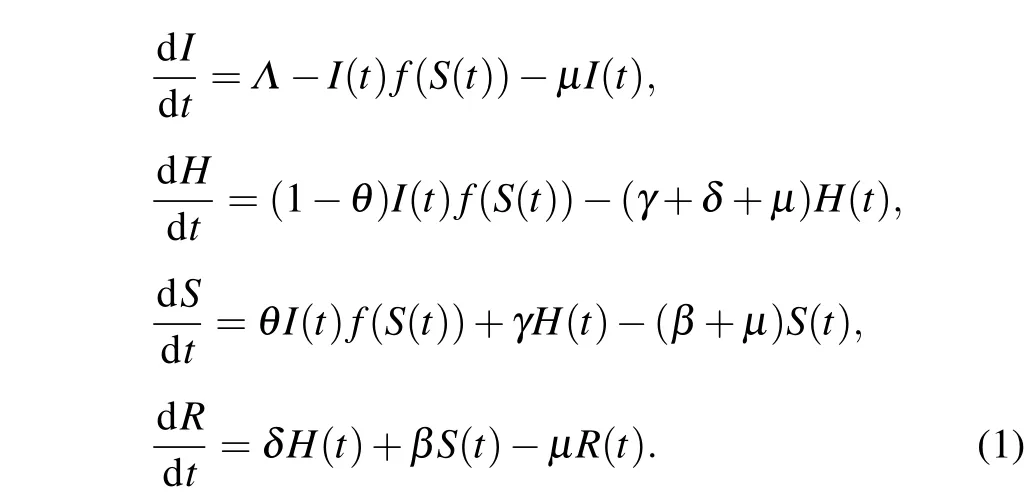
In sociology,I(t) represents individuals on online social networks who have never heard rumors or been contacted to forward rumors at timet,H(t) indicates those people that have heard rumors but hesitated to spread the rumors at timet,S(t)refers to those people who choose to believe and forward rumors but not actively create rumors at timet,R(t)means the people who have no interest to the rumors or no longer believe in rumors,and hence will not spread the rumors at timet. The functionf(·)represents the general incidence function. More sociological meanings about the parameters appearing in system(1)are explained in the sequel:

Λ:the number of entering individuals in the whole group;

μ:leaving rate of the population;

δ:conversion rate from hesitating individuals to stiflers;

γ:conversion rate from hesitating individuals to spreaders;

β:transmission rate from spreaders to stiflers due to lose interest in spreading rumors or forget rumors;

θ:portion of those hearing the rumor who will spread the it,andθ ∈[0,1].

However,in the real world,the individuals’psychological state(e.g.,hesitating,forgetting etc.) and individuals’behavior(e.g., forwarding, comment etc.) sometimes are disturbed by the environmental noise through the process of rumor dissemination. Therefore, in the noisy environment, the deterministic models not only have difficulty in fitting the data but also have strong limitations. Thus,it is meaningful to consider the influence of the social randomness in rumor propagation.More precisely,the effect of uncertainty should be considered in the parameters estimations, such as transmission rates between the four groups of people. Recently, some researchers have devoted in studying the rumor propagation models with stochastic perturbations,see e.g.,Refs.[7,12,14–16,37].From the literature,[38]it is known that the deterministic models can be transformed into stochastic models by introducing the time Markov chain,parameter perturbation,and robustness of positive equilibria to the deterministic models or the environmental noise that is proportional to the variables. This gives us the motivation to investigate the stochastic effect to the model(1).

Adding the environmental noise into the model(1),in this paper,we consider the following stochastic rumor propagation model:Using the method established by Khasminskii,[21]we provide the sufficient condition to guarantee the existence of an ergodic stationary distribution for system(2). The main result is stated as follows.

2. Preliminaries

To obtain the ergodic stationary distribution of system(2),we first recall some definitions and known results in the sequel.

Let (Ω,?,P) be a complete probability space with filtration{?t}t≥0satisfying the usual conditions(i.e.,it is right continuous and increasing while?0contains all P-null sets),and the values of all parameters are positive. Moreover, we denote

a∨b:=max{a,b}, a∧b:=min{a,b}for alla,b ∈R,

andC2,1(Rd×(0,∞);R+)by the function space consisting of all functionsV(x,t):Rd×(0,∞)→R+which are continuously twice differentiable inxand once int. Then we consider initial value problem of thed-dimensional stochastic differential equation:

3. Existence of an ergodic stationary distribution

Based on the assumptions (A1) and (A2), the right hand side of system (2) satisfies the local Lipschitz condition. Then, given any initial value (I(0),H(0),S(0),R(0))∈R4+, it is known that (2) admits a unique local solution(I(t),H(t),S(t),R(t))ont ∈[0,τe]for someτe＞0. Note thatτemeans the explosion time.[27]To derive the result of Theorem 1,we only need to show thatτe=∞a.s.

Proof of Theorem 1 Letn0be a large number such thatI(0),H(0),S(0),andR(0)all lie in the interval[1/n0,n0]. For each integern ≥n0,we define the following sequence of stopping time:

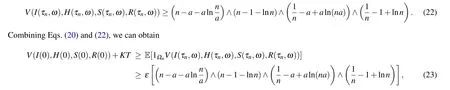
where 1Ωnmeans the indicator function ofΩn. Lettingn →∞,we have

To verify(H2),let us define theC2-nonnegative functionQ(·):R4+→R by

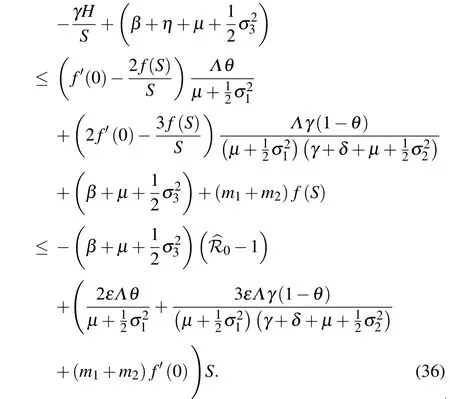
Summing up the above estimations,we can derive

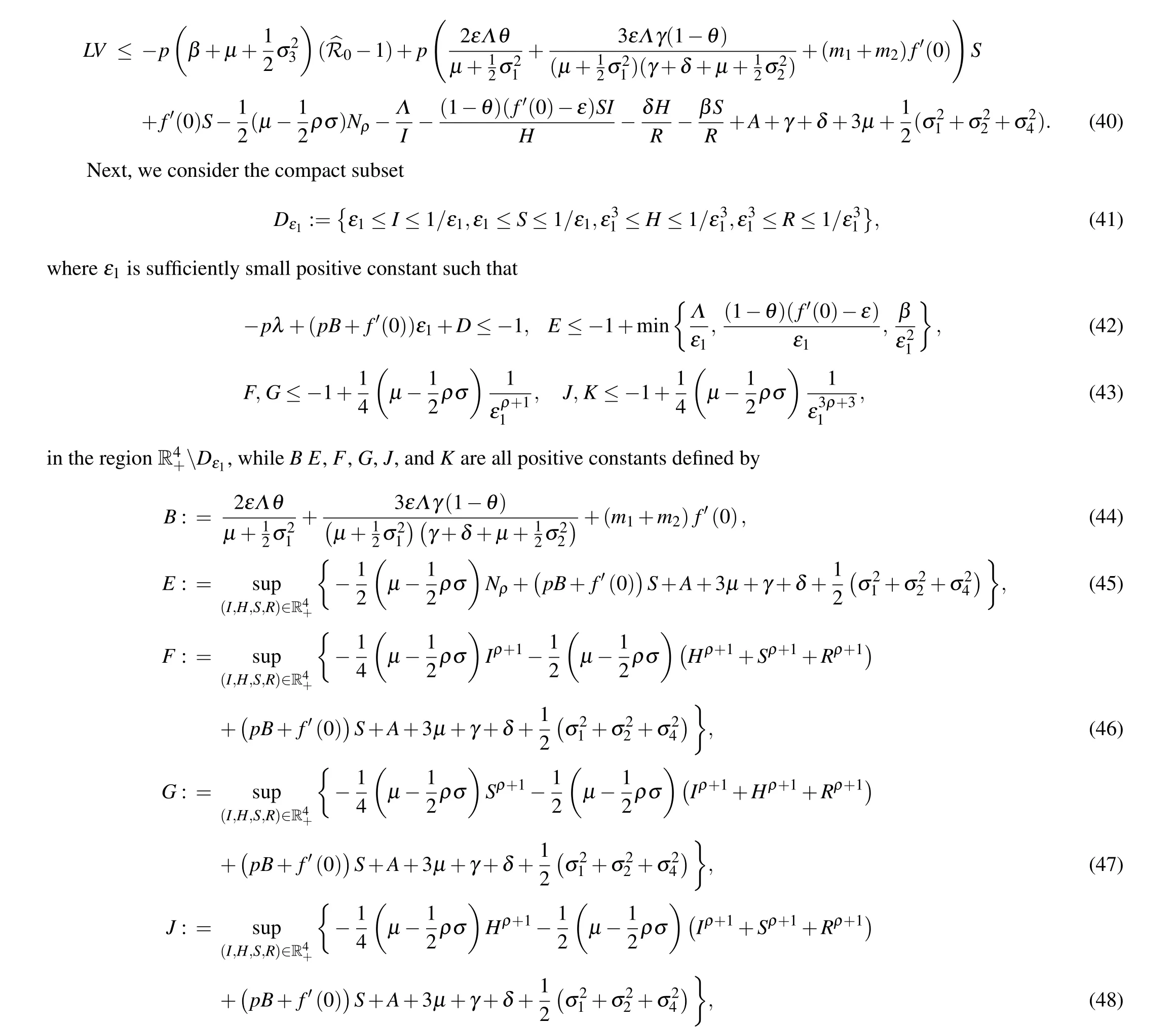
Then it follows from theF-inequality of Eq.(43)thatLV ≤-1 for all(I,H,S,R)∈D5.

By the first inequality of Eq.(42)and similar argument for Case 1, we can also prove thatLV ≤-1 for all (I,H,S,R)∈D2∪∈D3∪∈D4. Similarly, by theG,J,K-inequalities of Eq.(43)and similar argument for Case 2,we haveLV ≤-1 for all (I,H,S,R)∈D6∪∈D7∪∈D8. Therefore, the claim (50)holds,i.e.,the condition(H2)holds.

By Proposition 1, we conclude that system (2) admits a unique stationary distribution which exhibits the ergodicity.The proof of Theorem 2 is complete.

4. Numerical simulations

To better understand the theoretical results, we carry out some numerical simulations to illustrate the dynamic results of the stochastic rumor model under some parameters. Let us choose

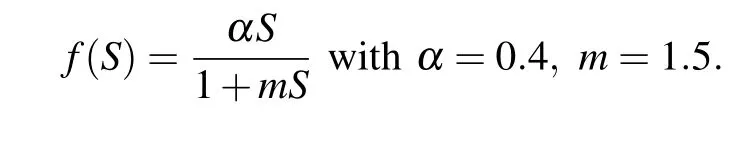
Then, by using the Milstein scheme,[11]the following discretization system is obtained:

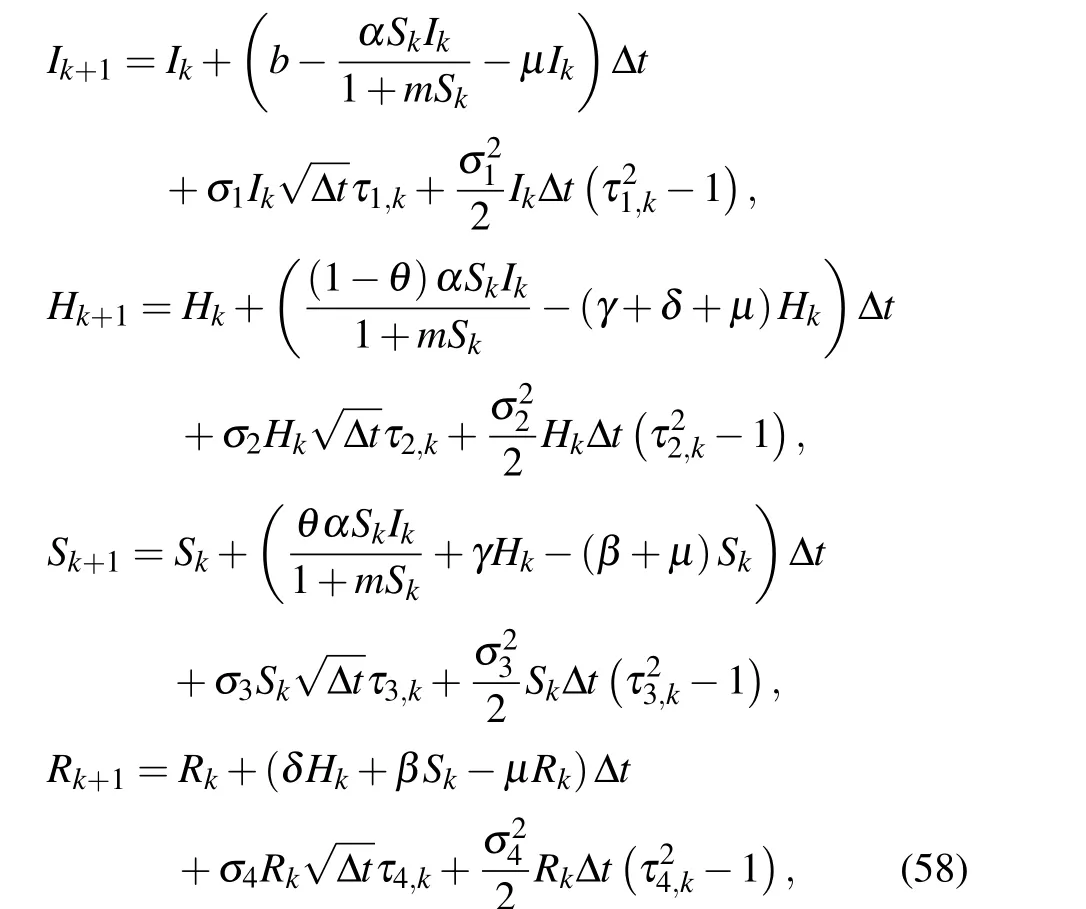
whereτi,k(i= 1,2,3,4) are four independent the Gaussian random variables withN(0,1)and time increment Δt ＞0. In addition, we assume that the values of parameters are as follows:

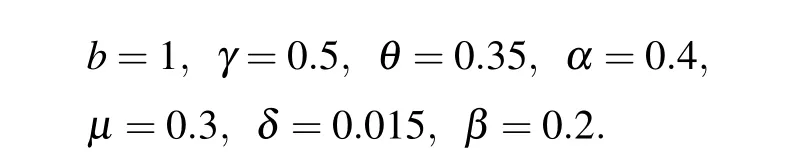
Next,through the numerical simulations of discretization system(58),we discuss its influence on rumor propagation from the following two aspects: the intensities of noise and key parameters.

4.1. Impact of the intensities of noise

From their density functions, one can also see that the solution of system (2) has a stationary distribution. In addition,the numerical results reveal the following interesting fact.

4.2. Impact of different parameters

In addition to the stationary distribution of model(2),we are also interested in what parameters will affect rumor propagation. Firstly, we analyze the contact transmission rateα,which is of great significance in communication because it is considered to be a key indicator to reflect whether rumors can be further spread. Here, under the same values of other parameters, we select different transmission rateα=0.1, 0.4,and 0.8 to study their influence on rumor propagation.

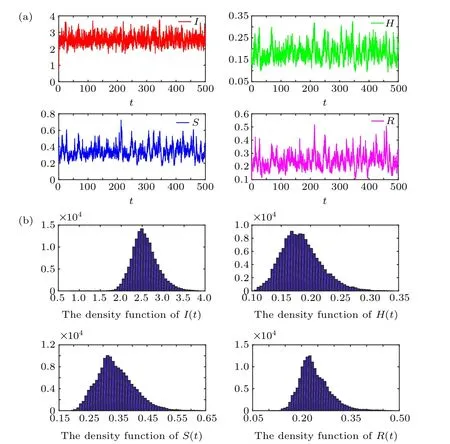
Fig.1. Stationary distribution of system(2)with σ1=σ2=σ3=σ4=0.1.Panels(a)and(b)represent the solution and the density function respectively.

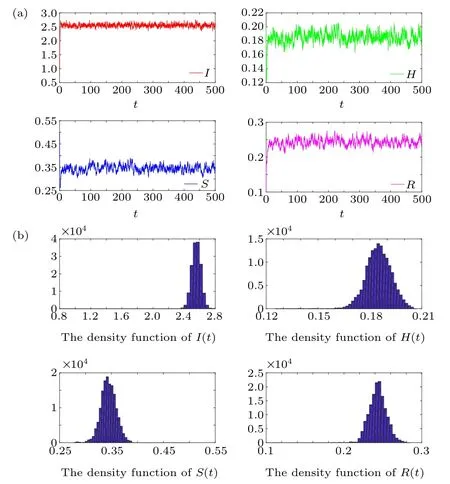
Fig.2. Stationary distribution of system(2)with σ1=σ2=σ3=σ4=0.02.Panels(a)and(b)represent the solution and the density function respectively.

From Fig.3,we observe that when the value of the transmission rateαis small, the number of rumor spreadersS(t)will decrease rapidly and is close to zero; when the value of the transmission rateαis big,the number of rumor spreadersS(t) will increase in the fluctuation, and the range of the oscillation will also keep increasing. This shows that reasonably cutting off rumor propagation channels is an effective method to curb rumor propagation on social networks. Especially in the case of emergencies,it is necessary to limit the flow,screen the relevant accounts and other methods to avoid serious negative impact.

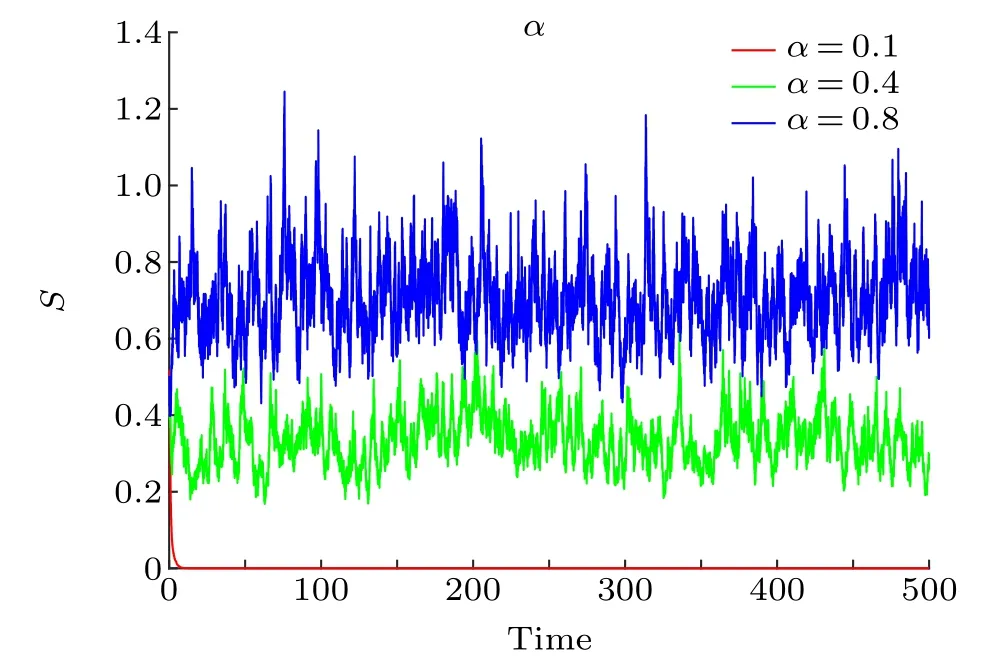
Fig.3. Trajectories simulations of rumor spreaders S(t)of stochastic rumor propagation model(2)is graphed for α =0.1,0.4,and 0.8.

Moreover,we discuss the influence of the conversion rate from rumor-hesitating individuals to spreaders on rumor propagation. Thus, we change the value ofγwhile keeping all other parameter values unchanged. As shown in Fig. 4, one can also see that as the value ofγincreases,the number of rumor spreaders increases,and the amplitude of oscillation also increases significantly under the interference of social environment noise.This shows that netizens express their opinions on rumors,which lead to rumor-hesitating individuals can not correctly judge the truth or falseness of information, so that the number of people fluctuates at every moment.In the meanwhile,some rumor-hesitating individuals believe and forward false information only based on the comments of some netizens,resulting in the continuous spread of rumors on the internet. Therefore, government departments should publicize the truth of emergencies to the public in a timely manner, eliminate the doubts of rumor-hesitant individuals,reduce the conversion rate from rumor-hesitant individuals to rumor spreaders,and effectively curb the spread of rumors.

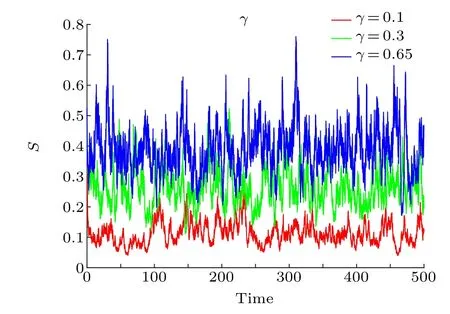
Fig.4. Trajectories simulations of rumor spreaders S(t)of stochastic rumor propagation model(2)is graphed for γ =0.1,0.3,and 0.65.

Besides the above mentioned,we believe that the scale of rumor spreaders is closely related to individual factors (such as the degree of interest in rumor propagation, and the degree of information memory and forgetting). Therefore, we investigate the influence ofβon the rumor spreaders under the premise of other parameter values unchanged.From Fig.5,we can see that with the increase of the value ofβ,the number of rumor spreaders shows a downward trend, and the amplitude of the oscillation also decreased significantly. This illustrates that whenβis small, rumor spreaders are vulnerable to the comments of netizens and constantly forward rumors to their friends around them; With the increase ofβ,the attraction of rumor propagation decreases,which makes the rumor spreaders lose interest in rumor propagation or forget rumors and have no intention to spread, and reduce the influence of rumor propagation. Therefore, government needs to strengthen science education for netizens,and timely release effective information to clarify the facts when an emergency occurs,then the value ofβwill increase correspondingly,so that the rumor will have less influence.

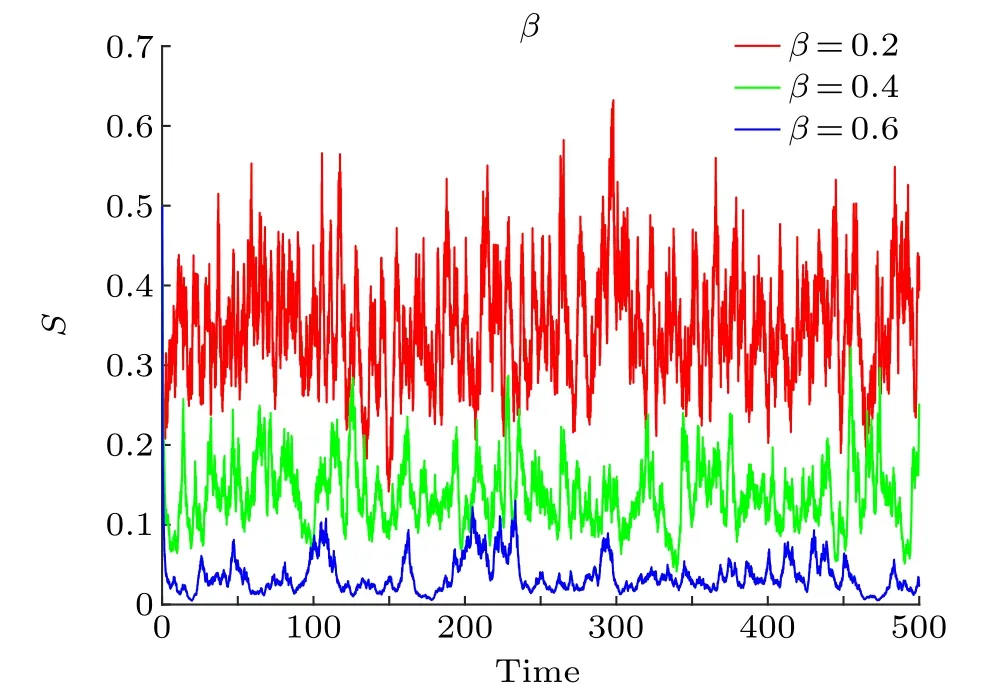
Fig.5. Trajectories simulations of rumor spreaders S(t)of stochastic rumor propagation model(2)is graphed for β =0.2,0.4,and 0.6.

5. A brief conclusion

In this paper, we propose and consider the dynamics of stochastic rumor propagation model(2)with general incidence function. In fact, we extend the classical rumor propagation model by introducing the random interference,and discuss the influence of random factors on the rumor propagation. More precisely,we show the existence of global positive solution of system (2) and provide some sufficient conditions to guarantee the existence of a unique ergodic stationary distribution.Furthermore,the numerical simulation results show that when?0＞1, the noise intensity has a great influence on rumor propagation. This means that when rumors diffuse in social media,the intensity of government control will play a key role in the rumor propagation.In addition,the change of parameter value will significantly affect the number of rumor spreaders,so as to provide decision-making departments with effective methods to control rumor propagation. Therefore,this work is helpful to analyze the rumor spreading model in theory and put forward corresponding measures for controlling rumor propagation. In practice, we can change the behavior of netizens by strengthening government intervention, authoritative media reports,publicity and education to wake up the awareness of netizens and other environmental interference factors,so as to reduce the interaction among ignorants, rumor-hesitant individuals and spreaders.

In addition to Theorems 1 and 2,we further illustrate the following interesting topics and leave them for our future consideration.

°Examining the existence of positive periodic solutions of system(2).

°Investigating the strategy to effectively control the dynamics of system(2).

°Extending our results to the case with L′evy noise, or other non-autonomous systems.

Acknowledgments

Project supported by the Funding for Outstanding Doctoral Dissertation in NUAA (Grant No. BCXJ18-09),the National Natural Science Foundation of China (Grant No. 72071106), and Postgraduate Research & Practice Innovation Program of Jiangsu Province, China (Grant No.KYCX180234).