基于地球坐標系的全球慣性導航與組合導航方法
王鑫耀, 王雙甲, 何梓君, 李榮冰*
(1.南京航空航天大學 導航研究中心,江蘇 南京 211106; 2.航空工業西安飛行自動控制研究所,陜西 西安 710065;3.空裝駐南京地區第四軍事代表室,江蘇 南京 210012)
極區導航是實現全球導航的重要組成部分,具備極區導航能力的現代飛機在全球航行中能突破航線規劃的制約,針對特定的飛行任務,若能夠飛躍極區則可以節省燃料和飛行時間,提升任務效率并增加經濟效益。
飛機在極區航行時,航行環境與常規地區有顯著不同。受極區特殊的自然環境影響,衛星導航、天文導航在極區面臨性能降低的問題,地磁導航、地形匹配導航則幾乎不可用。因此,面對極區特殊的航行環境,慣性導航系統不依賴外部信息的特性使其成為完成極區導航任務的主要導航系統。然而由于極區經線收斂并最終匯聚于一點,極點處北向無定義,地理坐標系失效,常規的指北方位慣導算法在極區存在計算溢出和誤差放大等問題,因此在極區不適用。
格網導航是解決極區導航問題的有效方法,但根據其機械編排,格網導航在赤道附近無法使用,不具備獨立完成全球導航任務的能力。如果采用指北算法和格網算法切換的全球導航方案,則2種機械編排的切換將使慣導算法無法統一,增加了算法的復雜性和工程實現的難度。
針對全球導航問題,文獻[1]提出了法向量的方法;文獻[2]研究了在通用的地心地固坐標系(Earth-Centered Earth-Fixed,ECEF)下的慣導機械編排,但導航參數的輸出仍在地球系下,物理意義不明確,不適用于近地導航。文獻[3]和文獻[4]闡述了完整的全球慣性導航算法。其中,文獻[3]提出了以游移方位慣導編排為內核的間接格網慣性導航算法;文獻[4]研究了基于偽地球坐標系的全球導航算法,但均沒有考慮慣導誤差累積的問題。文獻[5]和文獻[6]研究了基于地球系的慣性/衛星組合導航方法,均采用了松組合模式且沒有對導航參數如何輸出進行闡述。
為實現全球導航中慣性導航算法的統一,本文闡述了基于地球坐標系的全球慣性導航方法,并通過方向余弦矩陣將導航參數轉換至地理坐標系和格網坐標系,實現了導航參數的有效輸出。針對長航時慣性導航系統存在的誤差累積的問題,設計了基于地球坐標系的慣性/衛星緊組合導航濾波器,有效提升了導航精度。
1 基于地球坐標系的慣導機械編排
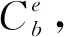
(1)
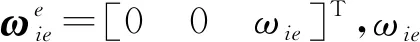
(2)
由比力方程可得地球坐標系下的速度微分方程為
(3)

由于經線在極點收斂,極點處經度無法表示,因此地球坐標系系下的位置用直角坐標表示為Re=[xyz]T,位置微分方程為
(4)
根據地球系慣導算法的機械編排,計算原理框圖如圖1所示。

圖1 地球系慣導算法機械編排
分析基于地球坐標系的慣導機械編排可知,地球系的慣導算法采用地球坐標系為導航坐標系,與飛機位置無關,不存在導航坐標系在極區失效的問題。在導航解算過程中隨著緯度的升高,直至到達極點附近,不存在趨于無窮大的計算項,避免了指北算法導航解算過程中誤差放大和溢出的問題。采用直角坐標表示位置,避免了在極點附近輸出位置時經緯度表示位置產生的誤差放大和奇異的問題。與格網算法相比,基于地球系的慣導算法力學編排更簡潔,計算量更小,且適用于全球導航。
2 基于地球坐標系的導航參數輸出
在全球導航任務中,基于地球系的慣導算法能在全球范圍內完成導航解算,不需要進行機械編排的切換,且相比于指北算法和格網算法計算量更小。但是地球系下的導航參數物理意義不明確,適用于內部解算但不適合對外輸出。因此考慮將基于地球系的慣導算法作為全球導航解算的內核,面對需要導航參數輸出的應用場景,則將參數轉換至地理坐標系或格網坐標系輸出。
中低緯度地區導航參數通常在地理坐標系下輸出;在高緯度地區,隨著緯度升高經線收斂,地理系下導航參數的誤差增大,在極點處地理系將失效,失去航向參考導致航向角無法表示。而格網坐標系以格林尼治子午線作為參考航向則可以避免導航坐標系在極區的失效,且格網航向在格網系輸出時誤差不發散。地球坐標系與地理坐標系、格網坐標系的關系如圖2所示。
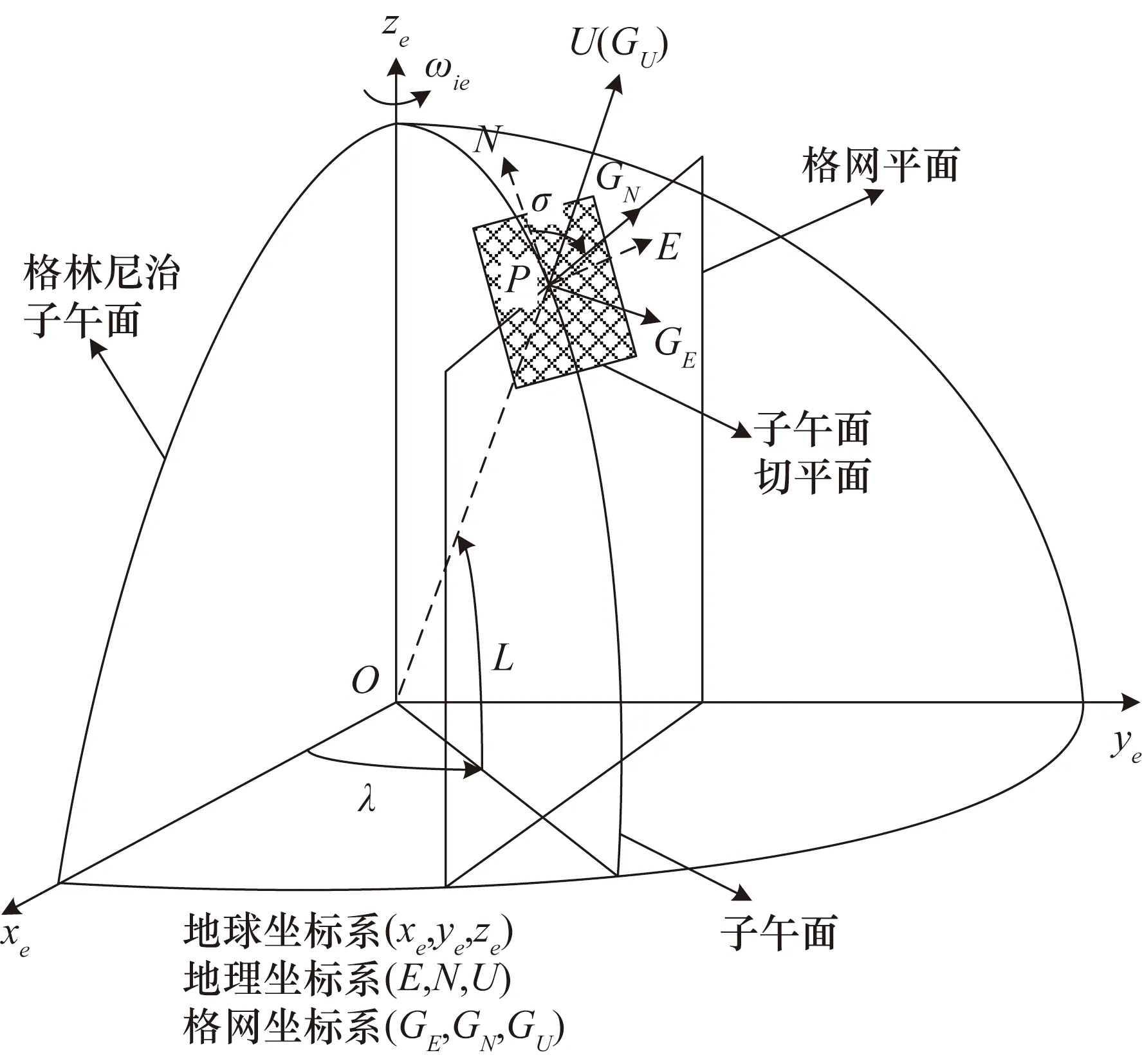
圖2 地球系與地理系、格網系的關系
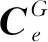
(5)
(6)
式中:λ為飛機經度;L為飛機緯度。
(7)
根據姿態陣可以得到格網系和地理系下飛機的姿態角。
地球系下的速度轉換至格網系和地理系表示為
(8)
基于地球坐標系的全球導航方法分離了慣導解算和參數輸出過程,其機械編排在地球坐標系下進行,實現了全球范圍內的統一,導航參數根據所處的緯度位置選擇在地理坐標系或格網坐標系下計算輸出。
對于衛星導航系統,通常以地球坐標系為導航坐標系,與本文的慣導機械編排一致,其輸出的地球系下的導航參數同樣可以通過方向余弦矩陣轉換至地理系或格網系,與慣導的數據進行對比驗證。
3 全球緊組合導航濾波器設計
基于地球坐標系的全球導航方法在極區應用中解決了導航系失效、計算誤差放大和溢出等問題,但無法避免慣性導航算法的固有特性,即系統誤差隨時間不斷累積,在長航時的任務中無法滿足系統精度要求,因此需要借助其他導航技術輔助慣性導航,通過組合導航修正系統誤差。
隨著北斗三號系統的建成,北斗在極區的信號質量和定位服務性能獲得了顯著提升,本節研究了極區慣性/衛星緊組合導航算法,以地球坐標系為導航坐標系,與慣性導航系統進行組合,并采用偽距組合的緊組合模式,緊組合的導航模式相比松組合具有更高的導航精度和魯棒性[8]。
全球緊組合導航系統總體架構如圖3所示,其中慣導解算與緊組合導航在地球系下進行,導航輸出在地理系與格網系下進行。
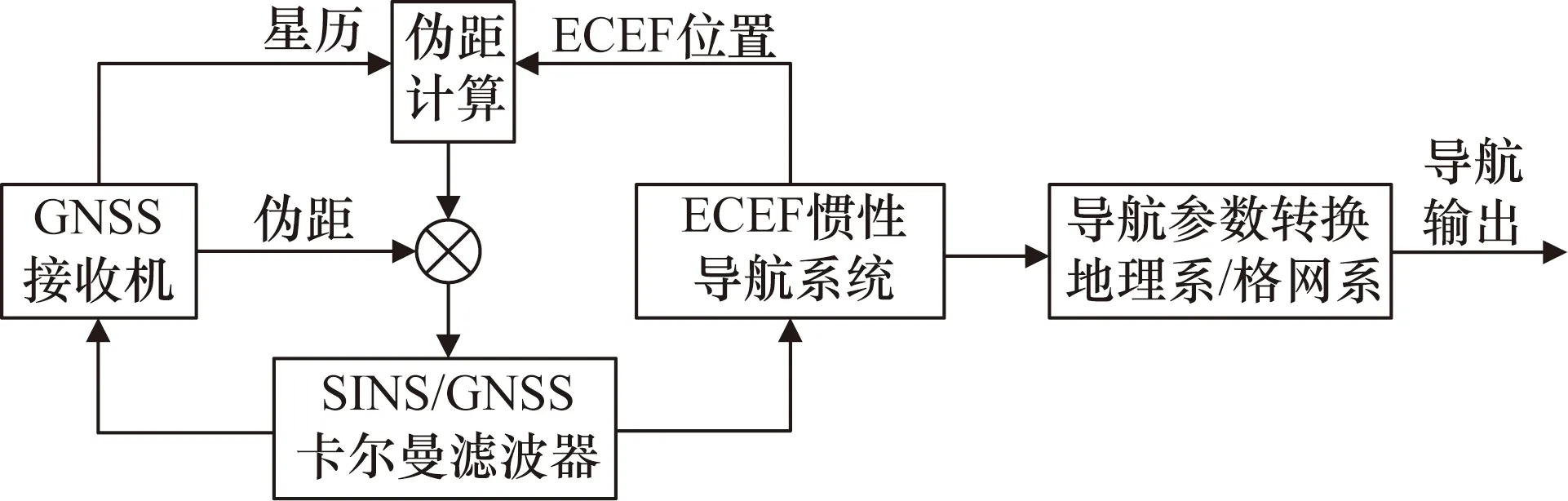
圖3 全球緊組合導航系統總體架構
3.1 系統狀態方程
卡爾曼濾波的狀態方程為
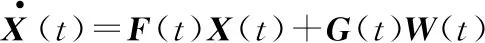
(9)
式中:F(t)為系統轉移矩陣;G(t)為系統噪聲矩陣;W(t)為系統噪聲。
濾波器狀態向量的INS部分包括15個狀態:
(10)
分別為地球系下的姿態、速度、位置誤差以及陀螺儀和加速度計誤差。
地球系下的姿態、速度和位置誤差方程[7]為
(11)

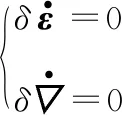
(12)
INS部分的系統矩陣為
(13)
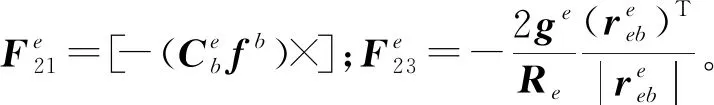
系統噪聲向量WINS(t)為陀螺儀和加速度計隨機噪聲:
(14)
系統噪聲分布矩陣G(t)為
(15)
(16)
系統矩陣、系統噪聲和噪聲分布矩陣分別為
(17)
合并INS與GNSS狀態方程,得到系統狀態方程為
(18)
3.2 系統量測方程
系統量測量為偽距,偽距量測方程為
Zρ(t)=Hρ(t)X(t)+Vρ(t)
(19)
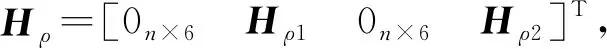
(20)
式中:(xu,yu,zu)為接收機在地球坐標系下的位置;(xsi,ysi,zsi)為第i顆可見星的位置;ρi為接收機到第i顆可見星的距離。
筆者基于卡爾曼濾波構建了地球系下的慣性/衛星緊組合導航濾波器,相比于常規的地理系下的松組合導航,適應了極區導航的需要,具備全球導航能力,且緊組合模式相比松組合具有更高的濾波精度。
4 基于地球坐標系的全球導航算法仿真
針對一定精度條件的慣性器件,對地球坐標系的全球慣性導航算法和緊組合導航算法進行仿真驗證。本次仿真利用航跡發生器產生飛行器航線上對應的飛行數據,并以該飛行數據為基礎,通過IMU仿真子系統仿真產生慣性導航系統所需要的相關數據。同時,針對典型的慣性傳感器的精度特性,加入系統誤差,對算法進行仿真。
4.1 仿真條件設置
仿真航跡設置如表1所示,飛機沿經線向北勻速飛行,飛行過程保持水平直線巡航。其中航跡1從高緯度地區出發并飛躍極點,航跡2始終在中低緯度地區。

表1 仿真航跡設置
基于生成的航跡利用數值解法反推可以得到理想的IMU數據,通過加入器件誤差仿真實際的IMU輸出。參考典型的慣性基準系統精度水平,設置慣性器件誤差參數如表2所示。
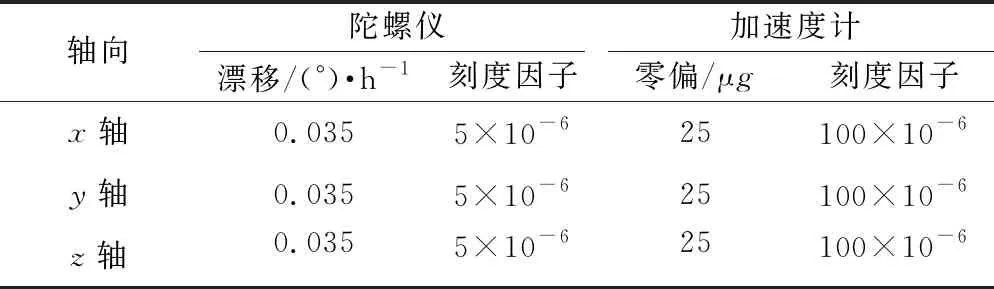
表2 慣性器件誤差參數設置
4.2 慣導系統仿真
首先對基于地球坐標系的慣導算法進行仿真,航跡1位于極區內,將地球系算法的仿真結果與格網算法進行對比的仿真結果分別如圖4和圖5所示,位置誤差在地球坐標系下表示,姿態角誤差在格網系下表示,航向為格網航向。
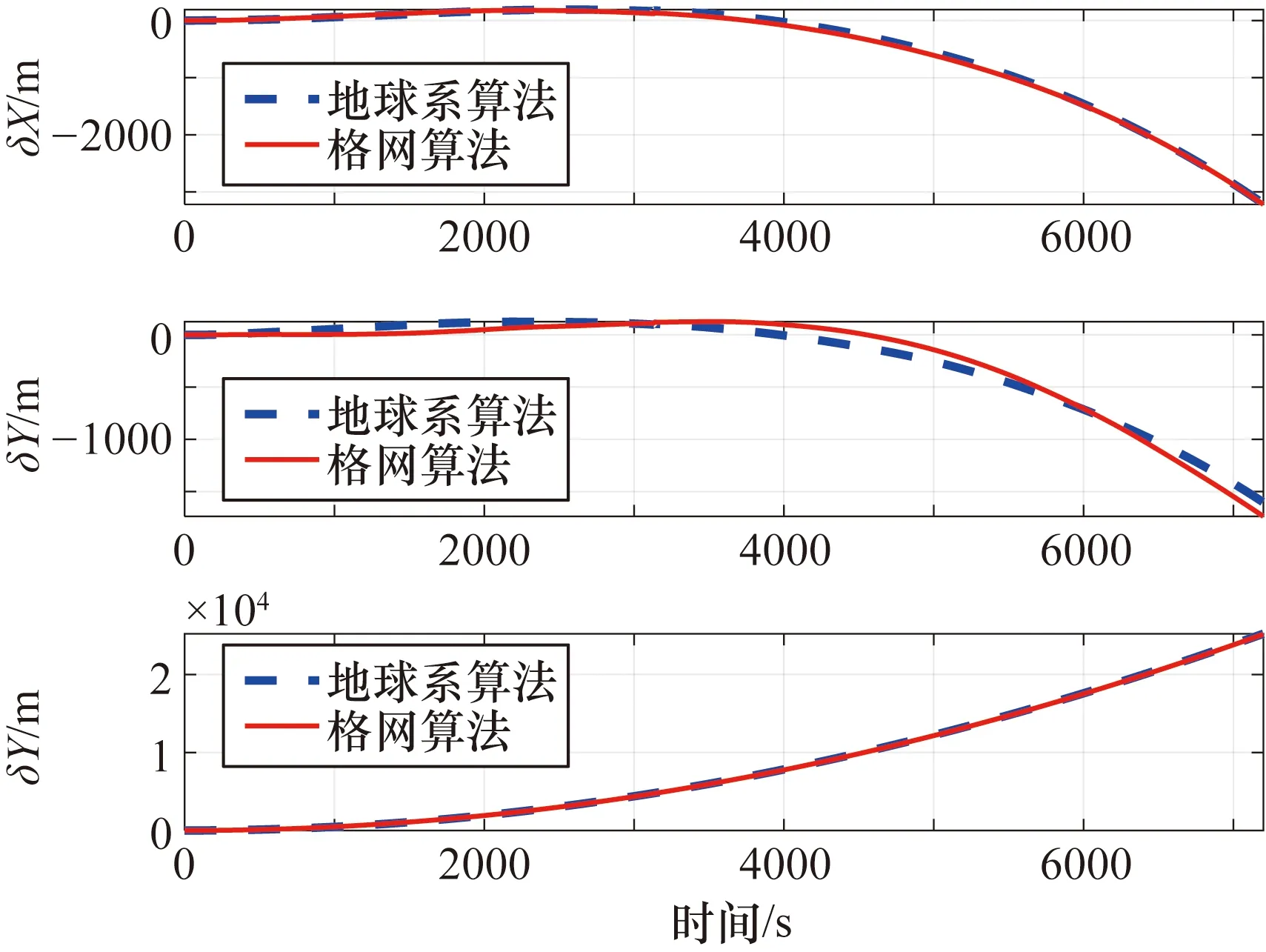
圖4 航跡1算法位置誤差仿真對比
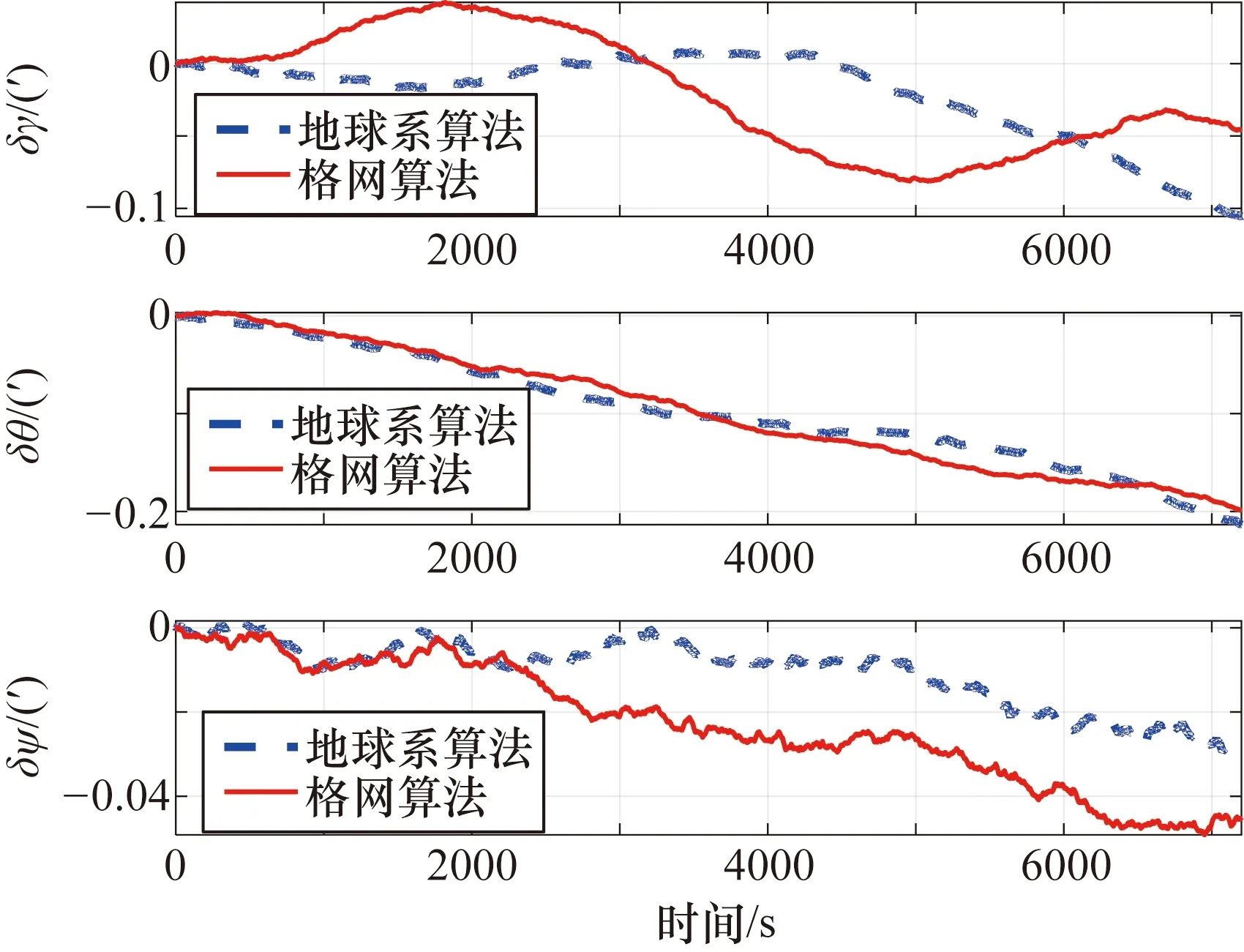
圖5 航跡1姿態角誤差仿真對比
航跡2位于中低緯度地區,將地球系算法的仿真結果與指北算法進行對比的仿真結果分別如圖6和圖7所示,位置誤差在地球坐標系下表示,姿態角誤差在地理系下表示。
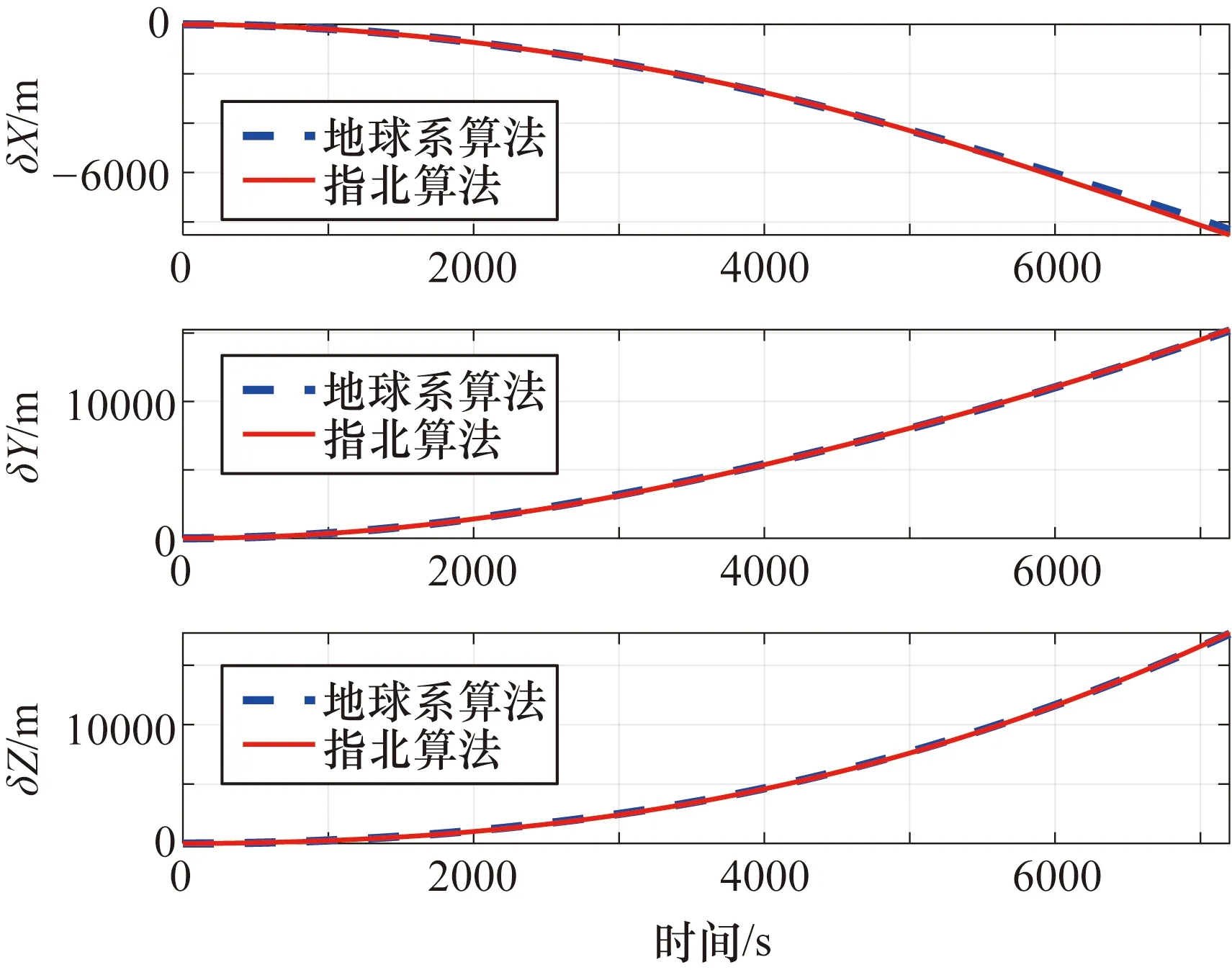
圖6 航跡2算法位置誤差仿真對比
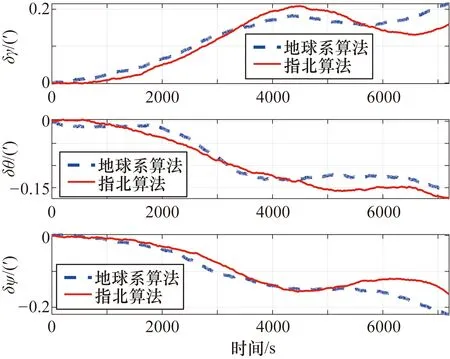
圖7 航跡2姿態角誤差仿真對比
分析仿真結果可知,基于所選的慣性傳感器精度水平,所實現的全球慣性導航算法在極區與非極區的性能分別與格網算法和指北算法的性能一致,驗證了全球慣性導航算法的有效性。
4.3 緊組合系統仿真
由于慣性導航系統的固有特性,在長航時的航行中系統存在誤差累積問題,如4.2節仿真結果所示,系統的位置誤差出現較大偏差。本文利用衛星輔助慣性導航系統,構建緊組合導航系統抑制誤差累積。
設置仿真衛星可見星數為10顆,位置精度因子(Position Dilution of Precision,PDOP)在2左右,偽距量測誤差為7 m,白噪聲為2 m。緊組合導航系統在極區與非極區的位置誤差分別如圖8和圖9所示。
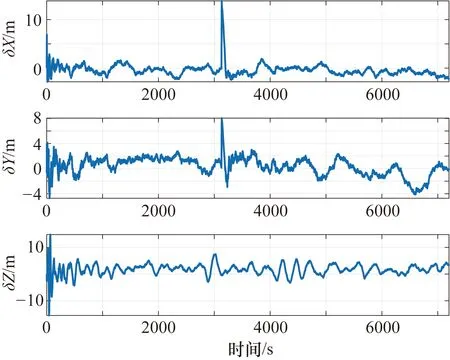
圖8 緊組合導航系統航跡1位置誤差
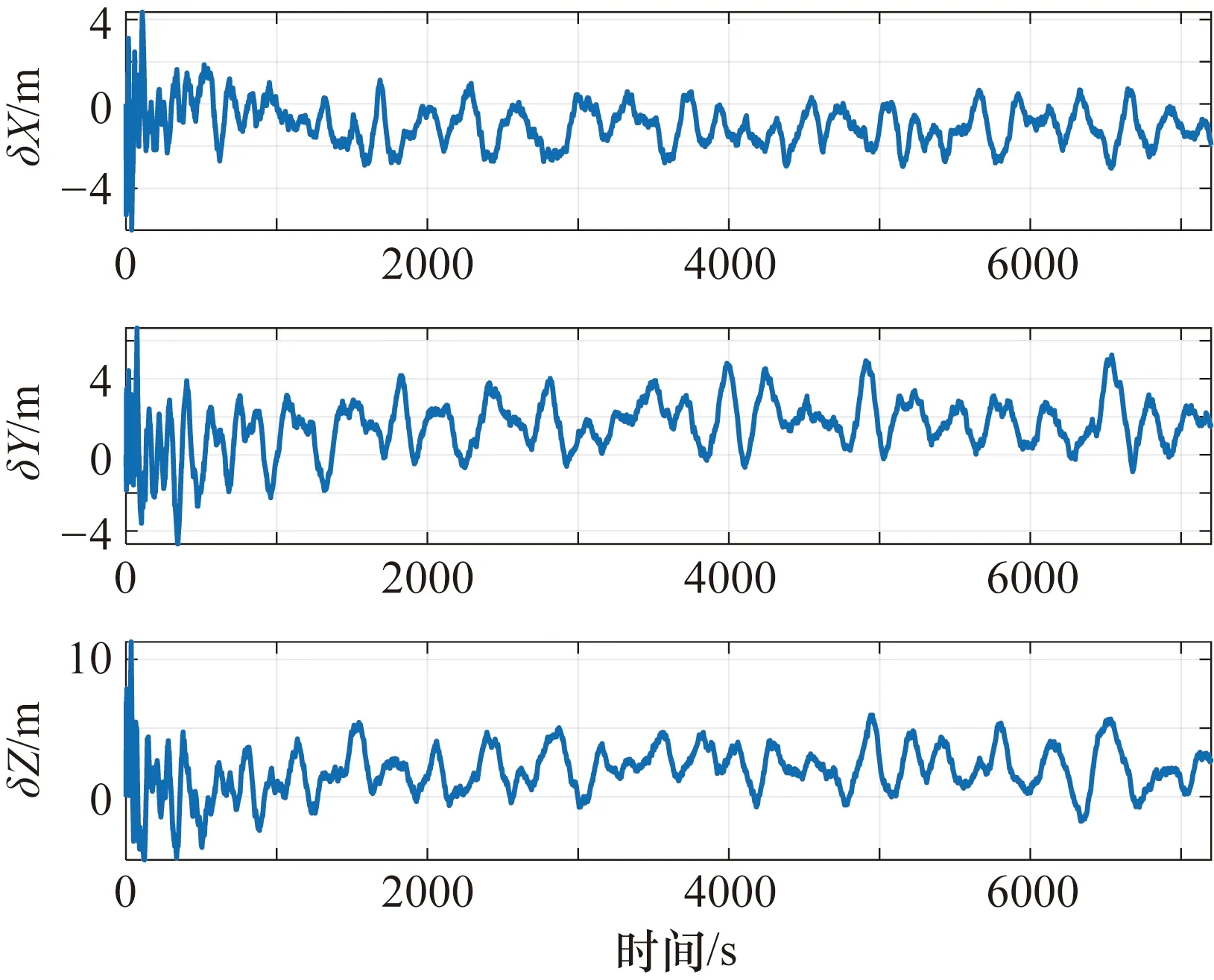
圖9 緊組合導航系統航跡2位置誤差
由仿真結果可知,緊組合導航模式下系統的位置誤差明顯減小且沒有出現發散,導航性能明顯改善,仿真結果驗證了緊組合對于抑制慣導誤差累積的有效性。
5 結束語
為實現慣導系統的全球導航,研究了基于地球坐標系的全球導航方法,將慣導系統的實現分為內在的機械編排和外在的參數輸出2個部分,實現了全球范圍內機械編排的統一和導航參數的有效輸出。針對長航時慣導系統誤差累積的問題,設計了慣性/衛星緊組合導航濾波器,有效提升了導航系統精度。
通過仿真對基于地球坐標系的慣導系統和緊組合導航系統的性能進行了分析。結果表明,全球慣性導航算法在極區與非極區的性能分別與格網算法和指北算法的性能一致,緊組合導航系統有效抑制了慣導誤差累積,提升了定位精度。

