簸箕形進水流道喉部高度對水力性能的影響

高傳昌，李曉超，董旭敏，高志鍇

（華北水利水電大學，鄭州 450045）

0 引 言

泵站進水流道按流道形狀分為肘形進水流道、鐘形進水流道和簸箕形進水流道［1］。簸箕形進水流道綜合了肘形進水流道和鐘形進水流道的特點，其高度較肘形進水流道低，寬度與鐘形進水流道接近，但沒有鐘形進水流道要求那么嚴格，流道型線簡單，施工方便，能有效防止漩渦的產生，已在荷蘭的泵站工程得到了廣泛的應用［2］。20世紀90年代以來，我國將簸箕形進水流道成功應用于劉老澗泵站、江西青山湖泵站、南水北調工程北京大寧調蓄泵站、江西南昌市新洲老泵站改造和湖北新灘口泵站改造等工程中［3-6］。

隨著這種流道在我國的推廣應用，國內學者就影響簸箕形進水流道水力性能的體型及其幾何參數進行了數值模擬和模型試驗，提出了簸箕形進水流道水力設計方法［7-11］。李四海等［12］就半圓型的簸箕與漸縮式的簸箕型流道的簸箕形式對流道水力性能的影響進行了數值模擬，結果表明，兩流道在各種工況下，內部流態良好，無漩渦或脫流。王亦曉等［13］為改善簸箕形進水流道水流狀態，提出了4 種不同長度的隔墩及后壁距的方案，并通過數值模擬計算分析，發現隔墩越長及后壁距越小可以分別改善喇叭口不同位置的壓力脈動情況。高傳昌等［14］就簸箕形進水流道3種進口收縮段寬度變化方案對流道水流流態的影響進行了數值模擬，結果表明，三種方案的流道水流流態均較好，但漸擴式簸箕形進水流道的水流流態略優。鄭云浩等［15］采用正交實驗法對簸箕形進水流道的后壁距、喇叭口直徑、吸水箱高度和底板傾角四個因素設計了9 種方案并進行了數值模擬，結果表明，喇叭口直徑對于泵裝置效率和揚程的影響最大。

簸箕形進水流道由反弧式進口段、簸箕形吸水室和喇叭管等3 部分組成［1］。進水前池的水流通過反弧式進口段后，沿著簸箕形吸水室轉向90°進入喇叭管進口。為了改善簸箕形吸水室流態，減少水流因轉向而引起的漩渦，簸箕形進水流道進口段常為逐漸收縮的反弧式進口段，進口段末端的斷面高度通常最小，因此稱為簸箕形進水流道的“喉部”，其高度被稱為喉部高度（或喇叭管懸空高度）。何鐘寧［16］、黃佳衛等［17］分別對鐘形進水流道和肘形進水流道喉部高度對流道水力性能的影響進行了研究，提出了在實際工程應充分重視進水流道喉部高度對進水流道流態的影響。陸林廣［18］分析了四面進水的進水流道水力設計準則，指出，過大的喉部高度不僅不利于水流均勻地從四面進入喇叭管，而且還會增加流道高度；過小的喉部高度將使喇叭管下方水流的速度加大以及速度方向的變化曲率加大，不僅造成水流紊亂，增加水力損失，而且直接影響到進泵水流的均勻性。

本文著重研究簸箕形進水流道喉部高度的變化對流道水流流態的影響，探究流道水力損失、流道出口斷面流速分布均勻度和速度加權平均角度隨流量的變化規律，以期對簸箕形進水流道的水力設計有所幫助。

1 計算方案

本文主要研究簸箕形進水流道喉部斷面的高度HB對流道水力性能的影響，并就其影響原因進行具體分析。簸箕形進水流道主要控制參數如圖1所示，在保證進水流道進口斷面高度Hj、流道進口斷面寬度Bj、流道長度XL、喉部寬度（喉部斷面寬度與進口斷面寬度Bj相同）、后壁距XT、喇叭管進口直徑DL、喇叭管高度HL和喇叭管內側輪廓線型等主要控制參數不變的情況下，選取5 種不同喉部高度進行數值模擬，計算方案如表1所示。

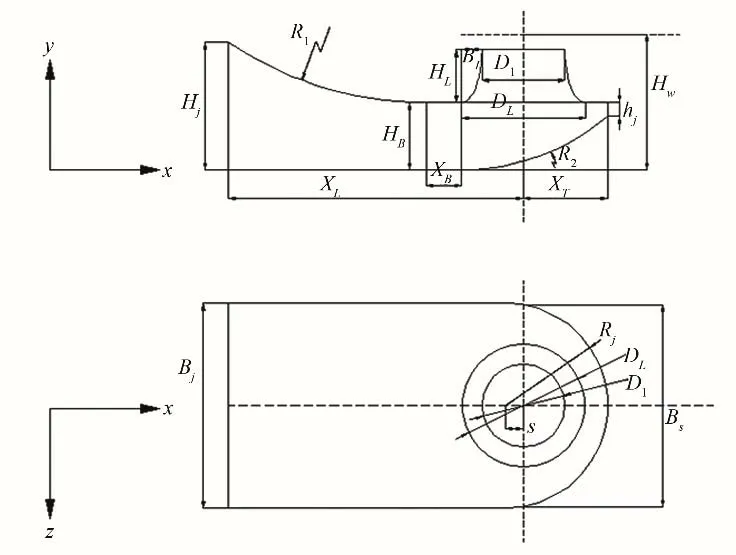
圖1 簸箕形進水流道主要控制參數圖Fig.1 Chart of main control parameters of dust-pan-shaped inlet conduit

表1 計算方案Tab.1 Calculation scheme

2 數值模擬計算方法

2.1 進水結構模型及網格剖分

采用ProE 軟件建立進水結構三維湍流模型，進水結構模型從前到后依次分為進水前池、進水閘室、簸箕形進水流道及其出口延長段4 部分，如圖2所示。整個進水結構模型使用Pointwise 軟件進行網格剖分，所有區域均采用六面體結構網格，并滿足網格控制參數要求。進水喇叭口附近流速梯度變化較大，網格局部進行加密。由于受壁面函數的約束，在邊壁處進行適當加密，使壁面處的y+保持在30～500 左右，以準確反映壁面處的水流流態。通過網格無關性檢驗，確定該模型最終網格數量為290 萬左右，滿足計算精度要求。簸箕型進水流道進水結構模型計算區域及網格圖如圖3所示。

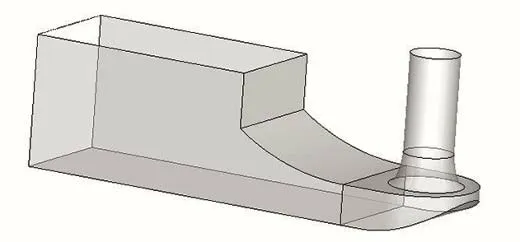
圖2 進水結構模型示意圖Fig.2 Schematic diagram of calculation area grid

圖3 網格剖分示意圖Fig.3 Schematic diagram of grid drawings

2.2 邊界條件

在對計算區域數值計算時，基于雷諾平均N-S方程，采用標準k-ε紊流模型。將計算域進口斷面延伸至前池距進水流道足夠遠處，可認為流速分布均勻，進口應用速度進口邊界條件。計算域出口斷面距流道出口斷面2 倍管徑處作為出口邊界，設置為自由出流條件。泵站進水池水面設置為對稱面，計算區域內的固體邊壁均為壁面，采用壁面無滑移邊界條件。

3 進水流道計算結果分析

3.1 反弧式進口段流速分布

取反弧式進口段的進口斷面、中間斷面和喉部斷面（簸箕形吸水室進口斷面）3 個斷面來反映反弧式進口段流道水流流動情況，圖4為設計工況下反映反弧式進口段3 個斷面的流速分布圖。由圖4可以看出：在5 個方案中，進口斷面的流速隨著喉部高度的增大分布相同；中間斷面流速分布有所差異，該斷面的頂部出現低流速區，且隨著喉部高度的增大低流速區范圍也在擴大；喉部斷面的流速分布差異較大，喉部斷面高度HB=0.7D0（方案1），斷面面積最小，沿斷面高度中心線對稱分布著2.2 m/s 中心流速區和2.0 m/s 流速區，斷面高度為HB=0.75D0時（方案2），斷面面積次小，分布著2.2、2.0 和1.8 m/s 三種流速區，2.2 m/s 中心流速區縮小到斷面的上部，而2.0 m/s 流速區居中，這2 個方案的中心流速比其他3 個方案大。當斷面高度HB=0.8D0時（方案3），2.2 m/s 中心流速區消失，2.0 m/s 中心流速區縮小到斷面的上部，而1.8m/s 流速區逐漸擴大且居中，斷面的周邊出現了1.6 m/s 流速區。喉部高度到達0.85D0（方案4）時，沿斷面高度中心線對稱分布著1.8 m/s 中心流速區和1.6 m/s 流速區，2.0 m/s 中心流速區消失.方案5 喉部斷面高度（HB=0.9D0）最高，斷面面積最大，除1.8 m/s 中心流速區縮小到斷面的上部和周邊出現1.4 m/s流速外，大部分斷面被1.6 m/s流速充滿。可見，隨著喉部高度的增大，喉部過流面積也增大，喉部斷面流速分布區不斷變化，從高流速區逐漸變化到低流速區。

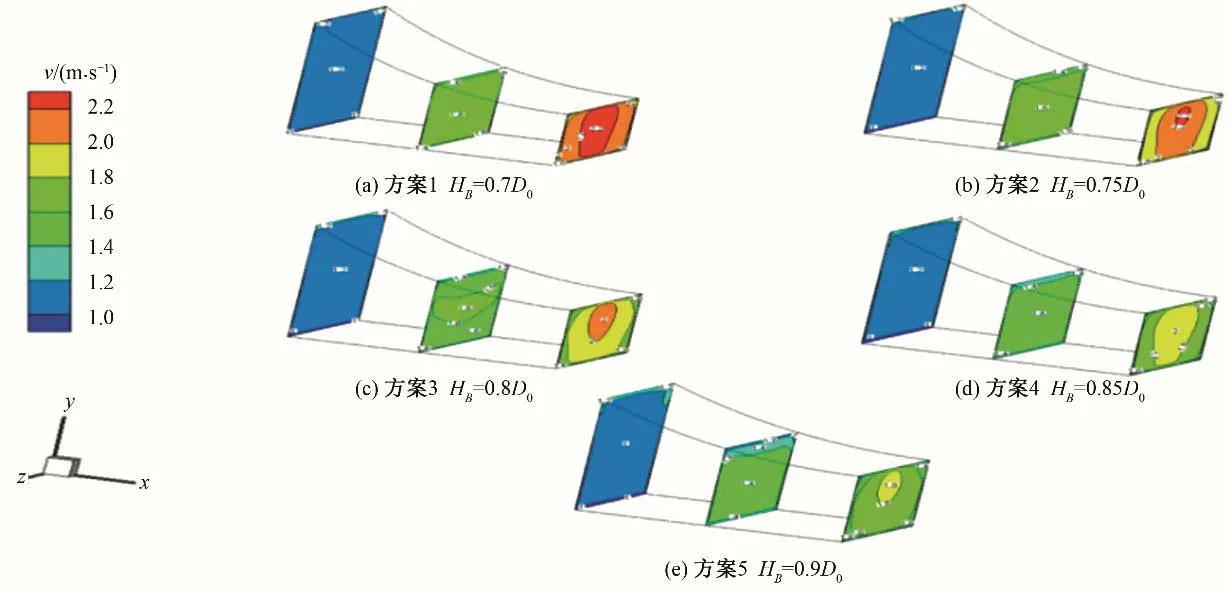
圖4 反弧式進口段截面流速分布圖Fig.4 The graph of cross-section velocity profile of the ogee inlet section

從對5個方案不同斷面流速分布分析可知，方案4和方案5不同斷面流速的變化和分布比較合理，方案1 和方案2 較差，方案3居中。

3.2 簸箕形吸水室出口斷面流速分布

喉部斷面的高度除直接影響簸箕形吸水室進口斷面（喉部斷面）流速分布外，也直接影響簸箕形吸水室出口斷面流速分布。根據數值模擬運算數據，作出設計工況下簸箕形吸水室出口斷面流速分布圖，如圖5所示。各方案流線總體平順，從四周流向簸箕形吸水室的后部，各方案的流速梯度由中部向周邊從高到低分布，高流速區（流速3.0 m/s以上）集中在簸箕形吸水室中部（喇叭管進口中心），呈月牙狀分布，低流速區（流速1.0 m/s以下）集中在簸箕形吸水室周邊。

由圖5可看出：高流速區范圍隨著喉部高度的提高先增大，而后又減小，低流速區范圍隨著喉部高度的提高的次序與高流速區范圍相反，先減小后增大；方案1 和方案2 在低流速區存在漩渦，且漩渦隨著喉部高度的提高而減小直至消失。出現這種情況可能是喉部高度影響了簸箕形吸水室底部圓弧半徑大小及其對吸水室過流斷面流速分布的影響。喉部高度低，吸水室底部圓弧半徑大，水流受到的離心力小，隨著喉部高度的提高，圓弧半徑減小，水流受到的離心力增大，同時簸箕形吸水室過流斷面隨著喉部高度的提高而增大，通過該斷面減小的水流流速小于受離心力增大的水流流速，高流速區范圍變大，低流速區范圍變小，而后隨著喉部高度的進一步提高，斷面減小的水流流速大于受離心力增大的水流流速，高流速區范圍變小，低流速區范圍變大。因此喉部高度居中的方案3高流速區范圍最大，低流速區范圍最小，而且流線分布較其他方案更為平順。

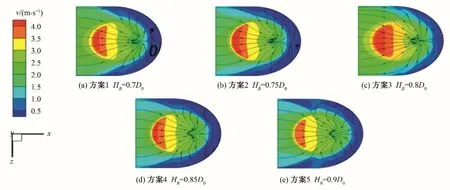
圖5 簸箕形吸水室出口斷面流速分布圖Fig.5 Flow velocity distribution at outlet cross-section

3.3 流道出口中心斷面流速分布

流道出口中心斷面包括喇叭管中心和簸箕形吸水室中心縱斷面兩部分（見圖1）。圖6為設計工況下的流道出口中心斷面的流速分布圖。如圖6所示，5種方案下的流線總體平穩，從兩邊呈對稱分布流向喇叭管進口，流速梯度從上到下由高到低分布，高流速區集中在喇叭管出口，低流速區集中在簸箕形吸水室斷面周邊。喉部高度（HB=0.8D0）居中的方案3 低流速區在底部兩角分布范圍比其他4個方案小，同時流線分布也較其他方案平順。

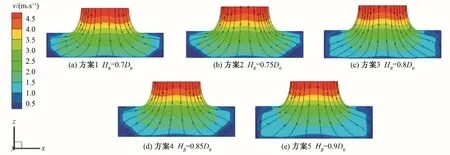
圖6 流道出口中心斷面流速分布圖Fig.6 Flow velocity distribution of outlet middie cross-section

3.4 進水結構中心斷面流速分布

取進水結構中心斷面反映流道內部流動的情況，經數值模擬后設計工況下的速度分布見圖7。從流速分布可以看出：各方案流道內的流線比較平順，僅是通過簸箕形吸水室的流線隨著喉部高度的提高逐漸由密變疏；喉部高度低的水流在吸水室出口轉垂直方向較好，喉部高度高的水流在吸水室出口仍未完全轉向垂直方向，水流經喇叭管整流后到達流道出口基本均與斷面垂直。5 個方案流道內的流態比較平穩，經過喉部的流速隨著喉部高度的提高由大變小，方案1 和方案2 從喉部2.5 m/s流速提高到吸水室轉彎處3.5 m/s 流速，分布較均勻；方案3 從喉部2.0 m/s 流速提高到吸水室轉彎處3.0 m/s，分布比較均勻；方案4 和方案5 喉部流速為1.6 m/s，到吸水室轉彎處流速分布為上高下低，從3.0 m/s 到2.0 m/s。水流進入轉彎后，各方案的4.5 m/s 高流速區從吸水室轉彎后內側發展到喇叭管內5.0 m/s高流速區。除方案3 以外，其他方案流道出口后的流速分布存在不同程度的低流速區。從整個進水結構流速分布看，方案3的流速分布優于其他方案的流速分布。

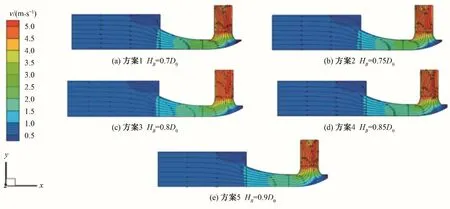
圖7 進水結構中心斷面流速分布Fig.7 Flow velocity distribution of middie cross-section of the inlet structure

3.5 進水流道水力性能評價

進水流道水力設計原則是盡量保證流道出口斷面流速分布均勻、水流流向垂直于出口斷面；為提高泵裝置效率，盡量減少流道水力損失。衡量進水流道出口斷面的流速分布均勻度、速度加權平均角度和流道水力損失的計算［19］，見式（1）～（3）：

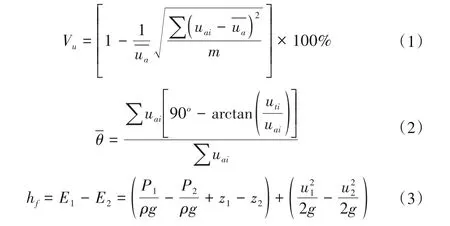
其中，流速分布均勻度和速度加權平均角度合稱為目標函數。Vu＝100%和θˉ＝90°為理想值，在進水流道設計中應使進水流道出口流速分布均勻度和速度加權平均角度最大限度地接近理想值，水力損失盡可能的小［19］。

為了分析5種喉部高度下的目標函數和流道水力損失隨流量的變化趨勢，在設計流量（918 m3/h）和最小流量（734 m3/h）范圍內取五個等分流量值計算，計算結果如圖8所示。由圖8（a）可以看出：在所選喉部高度范圍內，喉部高度對進水流道出口速度分布均勻度影響較大，且隨流量的變化具有不同的變化特征；當喉部高度小于0.8D0（方案3）時，流速均勻度數值隨著喉部高度的降低而減小，且隨流量的無明顯變化；當喉部高度大于0.85D0（方案4）和流量小于872 m3/h時，流速均勻度數值隨著喉部高度的提高具有逐漸增大的趨勢，但很不穩定，但當流量大于872 m3/h時，流速均勻度數值驟然下降，設計流量時達到最小值。出現這種情況可能是由于喉部高度的提高降低了喇叭管的高度，使進入喇叭管中的水流未能得到較好的調整，流量越大，可能喇叭管內的水流流態差，因此造成流速均勻度隨流量的增大而波動較大。在設計流量下，方案3 的流速均勻度為96.2%，高于其他4個方案的流速均勻度。

圖8 HB對流速分布均勻度和速度加權平均角與流量關系曲線Fig.8 Flow relation curves of HB and objective function and the hydraulic loss of conduit

從進水流道出口速度加權平均角隨著流量變化的趨勢看，如圖8（b）所示，各方案的速度加權平均角處于87.5°～88.5°之間，隨著流量變化的波動性相對較小，方案1的速度加權平均角最低，方案2最高，可見喉部高度大小對速度加權平均角的影響不大。在設計流量下，方案3 的速度加權平均角居中，為88°接近理想值。

由圖8（c）可看出：喉部高度對流道水力損失影響較大，在流量小于800 m3/h 時，喉部高度越小，流道水力損失越大；當流量大于800 m3/h 時，方案3 喉部高度（0.8D0）的流道水力損失均小于其他方案喉部高度的水力損失。一是喉部高度越小，加大了流道水力損失；二是喉部高度的提高，降低了喇叭管的高度，使進入喇叭管中的水流未能得到較好的調整，流場分布不均，加大了流道水力損失。可見，吸水室高度不宜過低或過高。在設計流量下，流道水力損失的次序為：方案1＞方案2＞方案3 和方案4＞方案3。

4 結 論

（1）喉部斷面的高度對簸箕形進水流道反弧式進口段的流速分布影響不大，主要對簸箕形吸水室和喇叭管的流速分布影響較大。

（2）喉部斷面高度過低，進入簸箕形吸水室的流速增大，增加了流道水力損失，流道出口斷面的流速分布均勻度與流量大小無關，速度加權平均角度隨流量的變化不大；喉部斷面高度過高，水流在吸水室轉彎處流速分布不均勻，到吸水室出口水流仍未完全轉向垂直方向，流道水力損失有所增加，流道出口斷面的流速分布均勻度隨流量的變化較大，速度加權平均角度隨流量的變化不大。

（3）結合各方案的簸箕形進水流道典型斷面的流速分布、流道出口的流速分布均勻度和速度加權平均角以及流道水力損失的分析結果，方案3 的流速分布優于其他4 個方案，而且流道出口的流速分布均勻度最高、流道水力損失最小，更加符合進水流道水水力設計要求。因此選取喉部高度HB=0.8D0的方案3為最優方案。