電助力自行車模型參考自適應扭矩控制研究

張懿， 陸騰飛， 魏海峰， 李垣江， 徐松

(江蘇科技大學 電子信息學院，江蘇 鎮江 212000)

0 引 言

近年來，以永磁同步電機作為主要驅動裝置的電動自行車已經成為我國交通體系中的重要組成部分，其中新興起的一種電動助力自行車以騎行者的踩踏力矩為基礎力矩，在起步、上坡等情況下電機輸出附加力矩，既延續了傳統自行車騎行輕便的特點，又具有起步輕松，上坡省力的優點。其中，當電動助力自行車在載重變化或者道路坡度變化時，助力扭矩如何計算成為研究的難點，助力扭矩的輸出效果決定了騎行者的騎行平穩性，更涉及到騎行者的安全。因此，助力扭矩控制方法的研究對電動助力自行車的發展至關重要[1-5]。

目前國內市場上出現的電動助力自行車控制系統主要分為無力矩傳感器的控制系統和有力矩傳感器的控制系統，其中無力矩傳感器的控制系統使用較廣，其控制原理為，使用霍爾元件測量騎行者的踩踏速度，通過助力比來計算電機的輸出扭矩，有力矩傳感器的控制系統則直接依據騎行者的踩踏力度來計算電機的輸出扭矩，采用這種控制方式的控制系統，電機的輸出扭矩對人的踩踏力有較強的跟隨性。文獻[6]提出建立擾動觀測器的控制方法，通過采集速度信號和踏板力信號來估計道路坡度和車身負載；文獻[7]提出一種基于模型跟隨控制的扭矩控制方法，通過處理速度和踩踏力信號來消除路面坡度和負載對車輛的干擾；文獻[8]為了提高估計精度，使用電機參數識別方法來估計在傾斜路面中施加的踏板扭矩；文獻[9]設計了基于神經網絡算法的電動助力車控制器，通過計算神經網絡回歸后的隸度函數，調節控制器速度環中的參數，對電機轉速進行實時控制，使電機輸出對腳踏速度有很強的跟隨特性。從上述方案研究情況來看，在無力矩傳感器的控制系統方案中，通過估算踩踏力信號來控制電機輸出扭矩，導致系統有較大的延時，無法獲得較好的跟隨性；在有力矩傳感器的控制系統方案中，電機輸出需要復雜的建模分析，對電機控制器的主控芯片要求較高，且無法保證整個系統的穩定性。

本文在有力矩傳感器的控制系統基礎上，提出可調增益模型參考自適應控制方法(model reference adaptive control，MRAC)，使用Lyapunov第二法推導MRAC可調增益自適應控制率，保證控制系統具有全局漸近穩定性[10-19]，該方法通過力矩傳感器獲得準確實時的踩踏力信號，系統對踩踏力信號實時監測捕獲，通過模型參考自適應算法計算電機輸出的力矩，以確保電機輸出的力矩對腳踏信號有很強的跟隨特性；數學模型簡單，對控制器資源占用率較小，且能保證系統的運行穩定性。并在MATLAB/Simulink中建立被控對象數學模型，通過仿真結果對比和實車路況測試輸出結果的對比，驗證在載重變化和坡度變化情況下該控制算法的有效性和可靠性。

1 電動助力車系統模型

電動助力自行車在不同路況行駛過程中，會受到來自不同方面的阻力作用，在水平路面上行駛會受到來自空氣的阻力、車輪與地面的摩擦力等，在上坡路面上行駛還會受到重力分量的阻力等，為了簡化分析，特做出以下假設：

1)忽略風阻等其他因素對助力車的影響，只考慮車輛載重和路面坡度兩個因素對其運行狀態的影響；

2)助力車直線行駛，忽略車輪與地面的相對摩擦；

3)電動助力車前后車輪直徑相同。

建立滿足上述假設條件的電動助力車縱向動力學模型，如圖1所示。

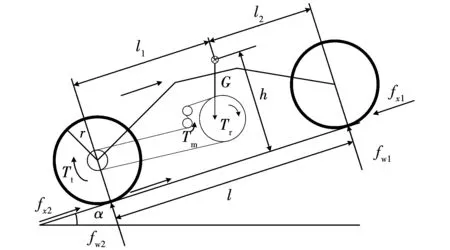
圖1 助力自行車縱向動力學模型

根據車輛整體受力分析，由縱向動力學模型可以得到：

(1)

(2)

式中：fw1、fw2分別為作用在前輪、后輪上的地面法向反作用力；G為助力自行車與騎行者的總重力；l1為助力自行車的重心到后輪中心之間的距離；l2為助力自行車的重心到前輪中心之間的距離；α為路面坡度；h為助力自行車與騎行者整體的質心高。由于助力自行車使用后輪驅動方式，根據力矩平衡分析前從動輪和后驅動輪的地面切向反作用力，即：

(3)

(4)

式中：fx1、fx2分別為作用在前從動輪和后驅動輪的地面切向反作用力；Tf1、Tf2分別為作用在前、后輪上的滾動力矩；r為前輪、后輪的車輪半徑。

根據上述分析，車輛系統動力學微分方程為

(5)

式中：Tt為驅動輪輸出扭矩；Tm為驅動鏈輪輸出扭矩；im為驅動鏈輪與后小鏈輪減速比；Tr為大鏈輪輸出扭矩；ir為大鏈盤與后小鏈輪減速比；Jr為驅動輪的轉動慣量；ω為驅動輪角速度；Fd為助力自行車驅動力，運動方程為

(6)

式中M為助力車與騎行者的總質量。

以上系統建模分析用于下面的助力扭矩控制算法研究。

2 模型參考自適應控制算法

模型參考自適應控制的系統結構如圖2所示。

圖2 模型參考自適應控制系統結構

模型參考自適應控制系統的基本工作原理為：設計參考模型，其狀態方程與被控對象的狀態方程一致，達到模型完全匹配的條件，參考模型的狀態方程參數設計即表明被控對象的理想輸出應如何對輸入信號做出響應，具體參數值經測試經驗得出，使參考模型的輸出結果ym符合可調系統的期望輸出響應，自適應機構根據參考模型輸出與被控對象輸出的差值產生一個自適應控制律，使被控對象的輸出或狀態逐步趨向于參考模型的輸出或狀態，最終獲得期望的可調系統輸出。采用Lyapunov第二法推導模型參考自適應系統的自適應律，與采用局部參數優化方法設計的自適應系統相比，該方法保證了系統具有全局漸近穩定性，并且在受到干擾時系統具有更好的動態特性。

圖3為可調增益MRAC系統結構。

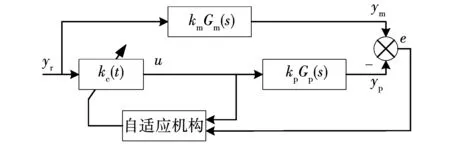
圖3 可調增益MRAC系統結構

設對象模型和參考模型的傳遞函數分別為：

(7)

(8)

式中kp為未知或慢時變的增益，km、n、ai、bi(i=0,1，…,n-1)均已知。控制器增益kc(t)用來補償對象參數kp，可調增益kc(t)的調節規律由Lyapunov第二法穩定性理論獲得，被控對象實際輸出趨向于參考模型輸出，差值e趨向于0。由圖3的系統結構可得

(9)

式中

k=km-kc(t)kp。

(10)

將式(9)轉化為狀態空間可觀規范型為：

(11)

ATP+PA=-Q。

(12)

選擇Lyapunov函數為

V=γ′xTPx+k2,γ′>0。

(13)

則

(14)

利用式(11)和式(12)得

(15)

(16)

由于kp未知或慢時變，可將其當作常數處理，則由式(10)得系統的自適應律為

(17)

由式(17)可知，此時的自適應律要求所有狀態變量可測，在應用中受到限制，需繼續變換。式(11)的傳遞函數G(s)=c(sI-A)-1b為嚴格正實函數的充要條件是：存在正定矩陣P和Q，使得：

(18)

(19)

式中，γ=γ′/kp為自適應律，γ>0。

式(19)的自適應律結構圖如圖4所示。

圖4 Lyapunov-MRAC系統結構

由圖4可知，系統的控制率為

u(t)=kc(t)yr(t)。

(20)

(21)

式中J為實際車輛模型中路面坡度、載重改變等外部因素影響下的等效轉動慣量。

根據式(21)，可以求得參考模型的傳遞函數為

(22)

式中：Jm為參考模型下的轉動慣量；Jf、Jr分別為車輛前后輪的轉動慣量。

綜上，電動助力車的模型參考自適應控制算法如圖5所示。

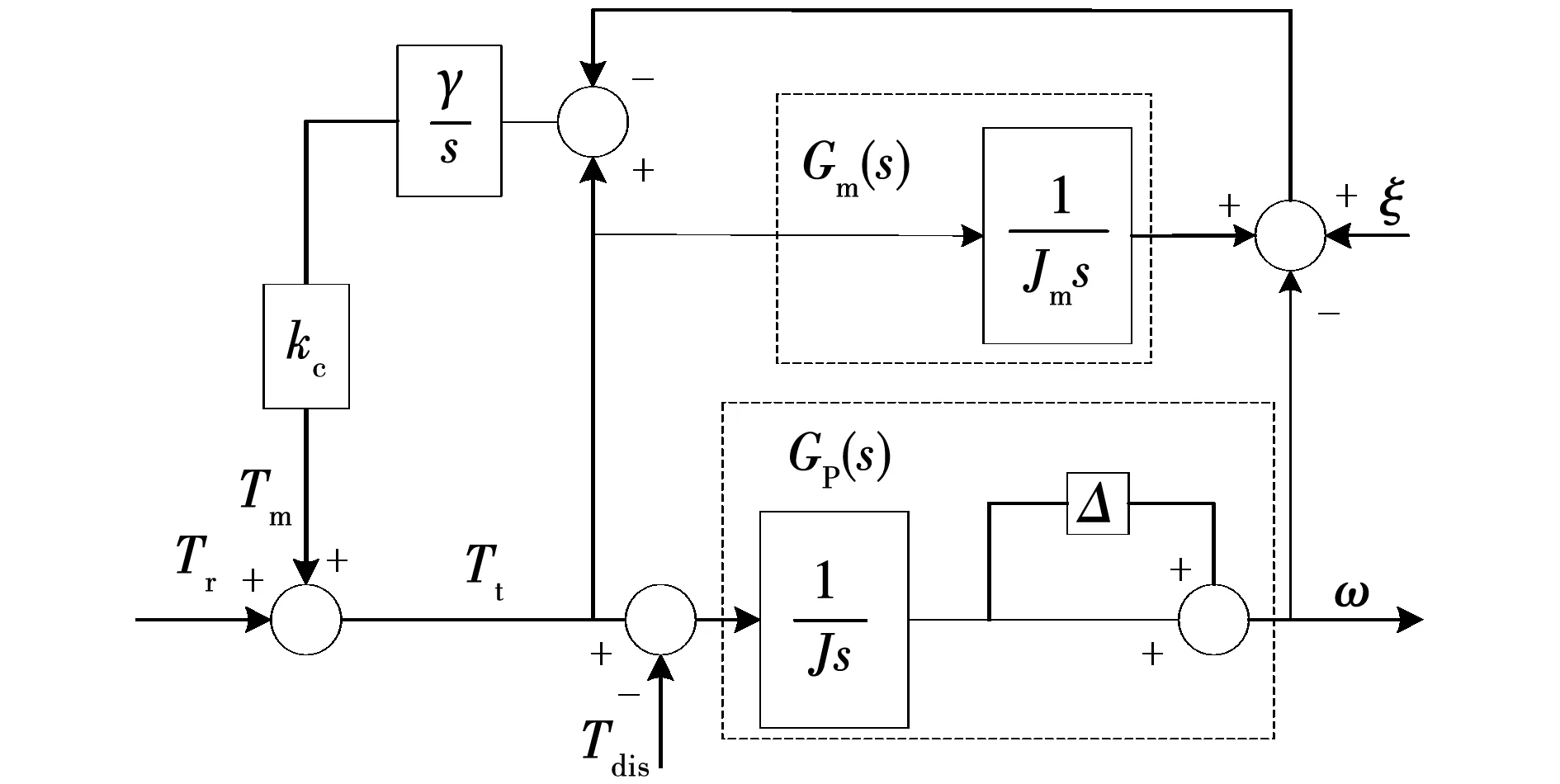
圖5 車輛自適應助力扭矩控制算法設計框圖

圖5中：騎行者踩踏力矩Tr作為系統輸入；驅動輪角速度ω作為系統輸出；ξ為傳感器噪聲；Tdis為坡度或載重變化造成的阻力矩；Δ為車輛對象模型內部參數變化。該自適應控制算法建立車輛在不同行駛狀態下的參考模型，在每個系統周期內，將車輛實際行駛狀態與參考模型的狀態對比，電機根據對比結果進行扭矩補償，使對象模型的輸出與參考模型的輸出一致，達到自適應調節扭矩的目的，電機輸出扭矩為

(23)

式中：為τ2電機的輸出扭矩；C為自適應增益系數；k為助力比；Tr為踩踏力矩。

3 仿真與實驗結果

為了進一步驗證算法的控制效果，將自適應控制方案與開環1:1控制方案作對比驗證。開環1:1控制方案采用無力矩傳感器的控制方案，使用霍爾元件測量騎行者的踩踏頻率，通過助力比來計算電機的輸出扭矩，其關系式為

τ1=kpf。

(24)

式中：τ1為電機的輸出扭矩；kp為助力比；f為踩踏頻率。在該控制方案中電機提供的助力扭矩與踩踏頻率成正比，當助力比為2時，關系曲線如圖6所示。

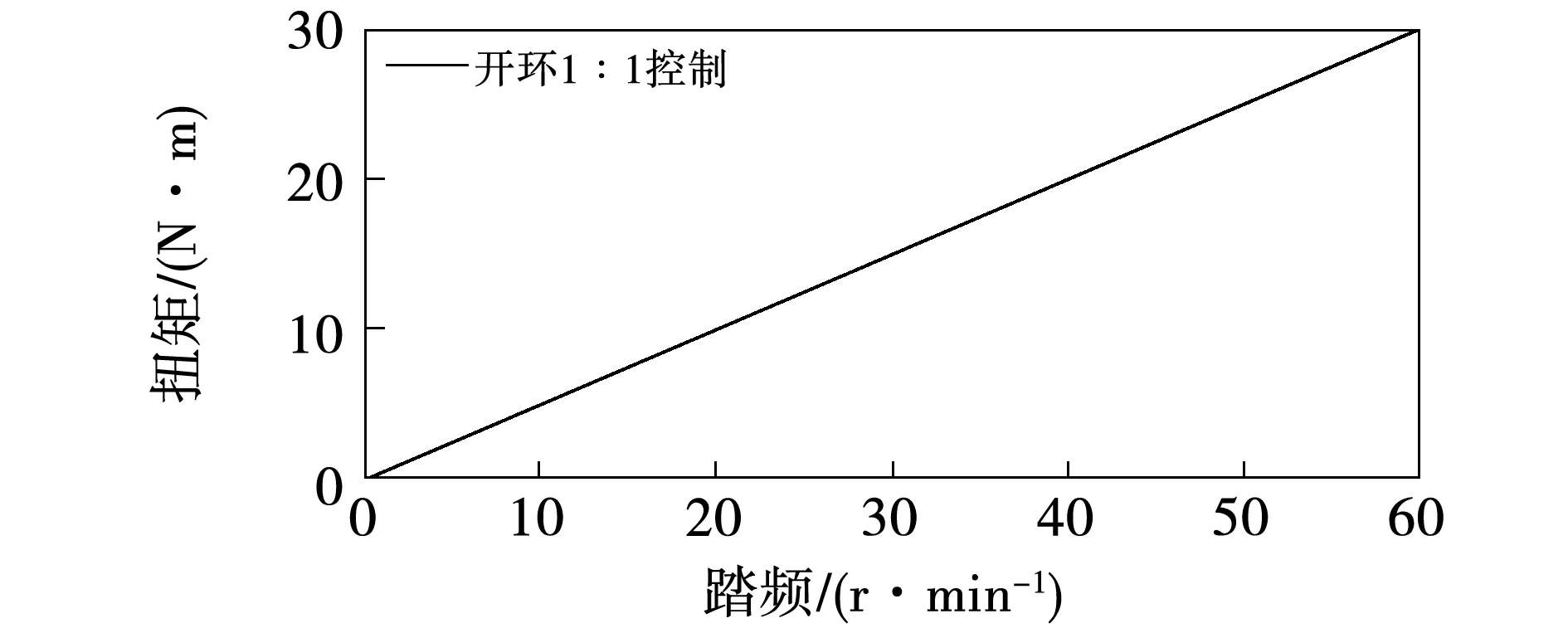
圖6 助力扭矩與踩踏頻率的關系曲線

實驗包括以下兩個方面：1)利用MATLAB/Simulink搭建自適應控制算法與整車模型，進行實時仿真驗證；2)搭建試驗平臺，通過實車路況測試驗證該算法的有效性。

3.1 MATLAB/Simulink仿真

基于模型參考自適應控制算法中的自適應增益系數與助力比相關，而在不同車速下助力比并不相同，因此需確定在不同車速下的自適應增益系數。根據工業標準，助力車的速度在25 km/h以下時，不同車速下電機提供的助力扭矩與踩踏力矩的比值不同，如圖7所示，助力比與助力車的行駛速度有如下關系：當車速在0～10 km/h范圍內時，助力比為2；當車速在10～25 km/h范圍內時，助力比為

圖7 助力比與車速的關系曲線

(25)

式中：k為助力比；v為助力車的速度。

為了保證助力自行車在使用自適應控制算法后的助力比仍能滿足上述比值，需要確定理想情況下的增益系數與車速的關系。在仿真設置中，設置載重60 kg，設置路面為水平路面，通過不斷調整自適應增益系數，獲得滿足上述關系的自適應增益系數與車速的曲線圖，如圖8所示。

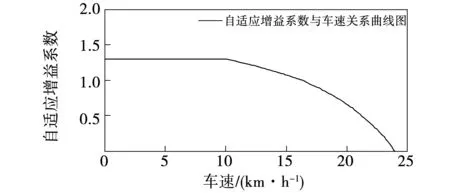
圖8 增益系數與車速的關系曲線

3.1.1 在不同載重下的仿真分析

在仿真設置中，設置電機模塊為三相、正弦波激勵的PMSM電機，設置電壓源為36 V，設置載重為單一變量，車輛載重分別為60、90 kg，設置路面為水平路面，給定15 N·m恒定踩踏力矩和18 r/min恒定踩踏頻率。在仿真分析中，為保證算法對比效果，設置車速與踩踏頻率無關，消除踩踏頻率對車速的影響，著重比較在不同算法控制下助力扭矩的控制效果。固定踩踏頻率是為了保證開環1∶1控制情況下，電機輸出助力扭矩的穩定性，仿真中的車輛加速依靠電機輸出的助力扭矩。記錄在自適應控制算法下的車輛行駛速度，電機輸出扭矩和負載扭矩，并與開環1∶1控制系統輸出結果作比較，對比結果如圖9所示。

由圖9(a)、(b)對比可知，采用開環1∶1控制情況下，改變車輛載重對車速影響較明顯；采用自適應控制情況下，車輛載重的變化對車輛速度影響較小，說明基于模型參考自適應的控制算法具有良好的載重適應性能。

由圖9(c)可知，采用開環1∶1控制情況下，電機扭矩只與踩踏頻率有關，因此在載重變化時，電機扭矩保持恒定，無法達到隨載重變化的理想效果；采用自適應控制情況下，電機扭矩跟隨載重變化做出自適應調節，在車輛起步階段，電機輸出較大助力扭矩，隨著車速上升，助力扭矩逐漸減小，在車速達到國家限速標準25 km/h后，系統停止輸出助力扭矩，滿足助力比與車速的關系曲線圖。

在理想的無摩擦狀態下，且電機不經減速器等環節而直接作用在負載上，助力自行車的電磁轉矩等于輸出轉矩，因仿真中轉軸、方向相同，故負載扭矩為踩踏力矩與電機助力扭矩的矢量疊加，負載扭矩隨時間的變化曲線如圖9(d)所示。

圖9 在水平路面上及60、90 kg載重條件下的仿真結果

助力自行車首先帶有60 kg負載騎行，在27 s車速穩定時額外增加30 kg負載，在45 s車速穩定后，減掉30 kg負載，在該運動過程中，電機的輸出扭矩變化曲線如圖10所示。在自適應控制情況下，負載增加時，助力扭矩也隨之變大，在減掉負載時，因車速已達到25 km/h，電機保持無助力扭矩輸出，充分了證明自適應控制方法的有效性。

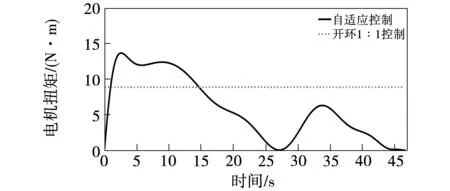
圖10 在水平路面、載重改變條件下的仿真結果

3.1.2 在不同坡度路況下的仿真分析

在仿真設置中，設置電機模塊為三相、正弦波激勵的PMSM電機，設置電壓源為36 V，設置路面坡度為單一變量，由水平路面分別進入10%、20%坡度的路面，設置載重為60 kg，給定15 N·m恒定踩踏力矩和18 r/min恒定踩踏頻率。記錄在自適應控制算法下的車輛行駛速度，電機輸出扭矩和負載扭矩，并與開環1∶1控制系統輸出結果作比較，對比結果如圖11所示。

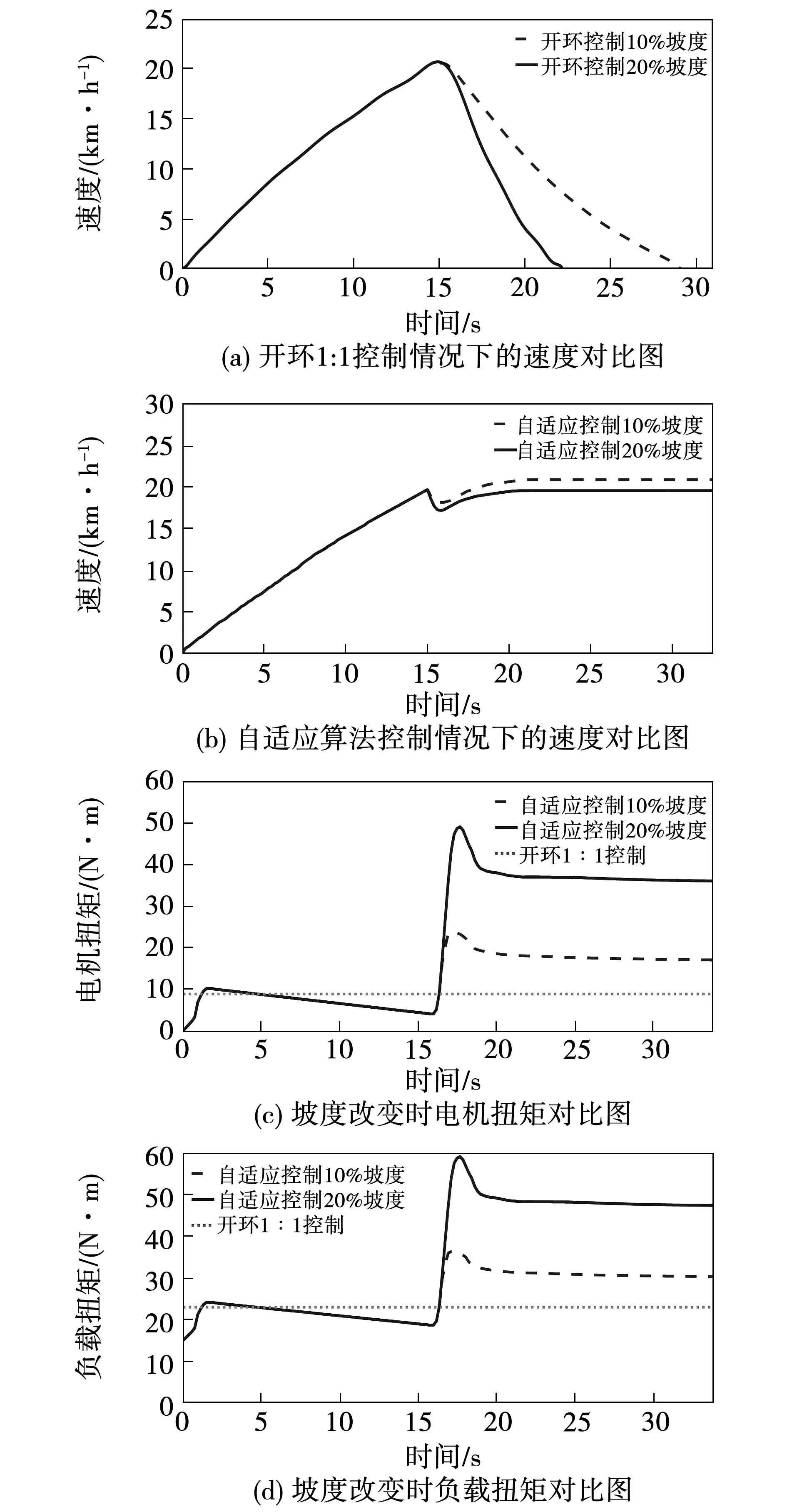
圖11 在10%、20%坡度路面上及60 kg載重條件下的仿真結果

由圖11(a)、(b)對比可知，采用開環1∶1控制情況下，車輛由水平路面進入上坡道路后，系統受到較大干擾，車輛速度下降較為明顯；采用自適應控制情況下，車輛上坡后，會經歷一個時間較短的減速階段，經自適應機構調節后，電機輸出扭矩增大，車輛仍能保持穩定上坡行駛，說明基于模型參考自適應的控制算法具有良好的路面坡度適應性能。

由圖11(c)可知，采用自適應控制的情況下，電機扭矩跟隨路面坡度變化做出自適應調節，保證在上坡路面維持較為穩定的車輛行駛狀況。

負載扭矩隨時間的變化曲線如圖11(d)所示，因仿真中轉軸、方向相同，故負載扭矩為踩踏力矩與電機助力扭矩的矢量疊加。

助力自行車在16 s時由水平路面進入10%坡度的路面，在26 s時由10%坡度路面進入20%坡度的路面，在33 s進入下坡道路，在該運動過程中，電機的輸出扭矩變化曲線如圖12所示。在自適應控制情況下，坡度改變時，助力扭矩會隨之改變，使騎行人員可以輕松爬坡，在下坡速度到達25 km/h時，電機停止輸出助力扭矩。

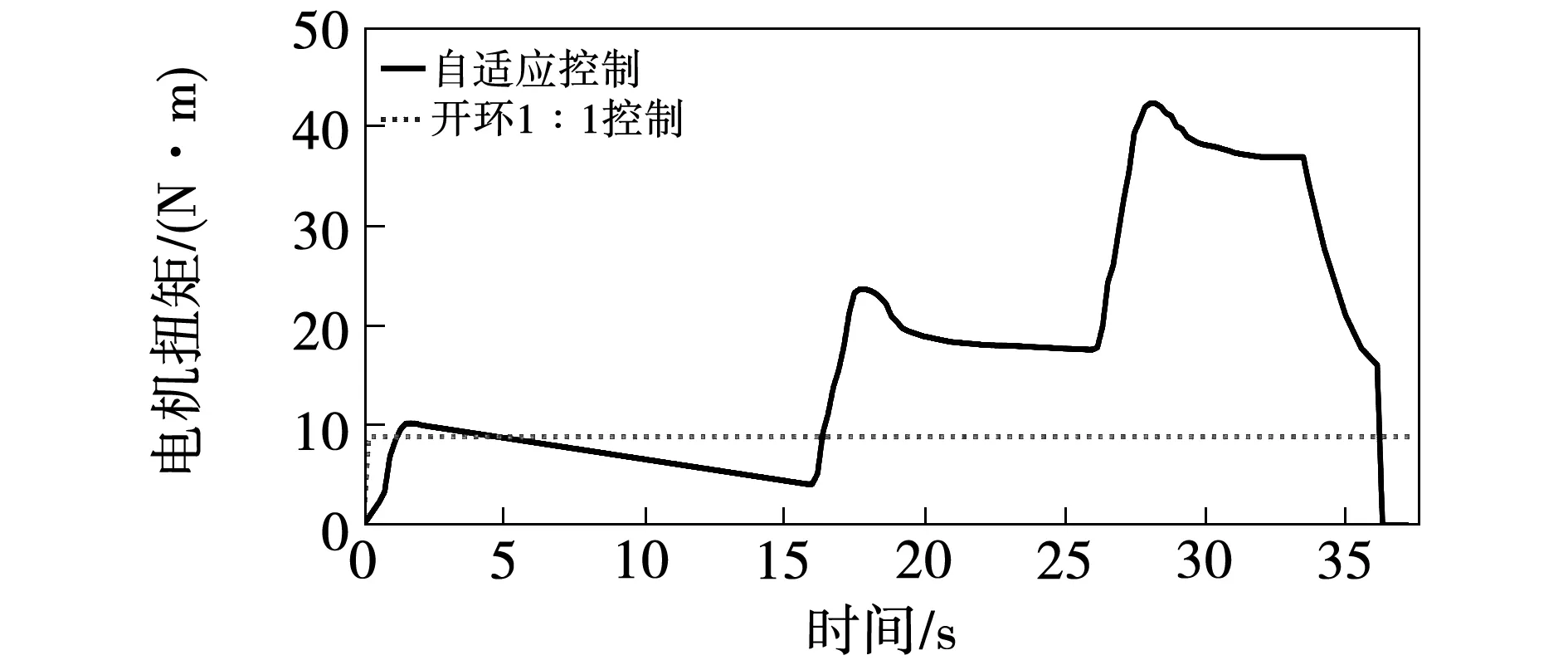
圖12 在坡度改變的路面、60 kg載重條件下的仿真結果

3.2 實車路況實驗

為了對自適應扭矩控制算法進行實驗研究，在某助力自行車上進行實車測試，所用助力車和力矩傳感器如圖13所示。

圖13 電動助力車實物圖

該電動助力車包括車架、鋰電池、中置電機、電機控制器、力矩傳感器、功能儀表等部件，具體參數如表1所示。

表1 電動助力車參數

助力車行駛過程中騎行者的踩踏力矩輸出無法保證恒定，為遵循單一變量原則，實驗時在控制器軟件層面給定恒定踩踏力矩，保證輸入量統一，在不同車速下動態給定自適應增益系數，給定關系如圖8所示，車輛騎行人員始終保證為同一人，體重約為60公斤。在車輛實際載重變化或者坡度變化情況下，記錄在自適應控制情況下的車輛行駛速度和相電流，并與開環1∶1控制系統輸出結果作比較。

3.2.1 載重騎行實驗

實驗條件設置如下：電動助力車在平坦筆直道路上行駛，無障礙物干擾；控制器軟件層面設置恒定踩踏力矩為15 N·m和18 r/min最大踩踏頻率；車速與踩踏頻率有關，車輛加速由踩踏頻率和助力扭矩共同作用。通過在車輛上增加30 kg負載物品來區分有無負載。

在開環1∶1控制情況下，給助力車增加30 kg負載后，起步速度明顯變慢，如圖14所示，這是因為此時電機提供的扭矩仍然是由15 N·m的踩踏力矩計算而來的，導致加速度減小，起步速度變慢。

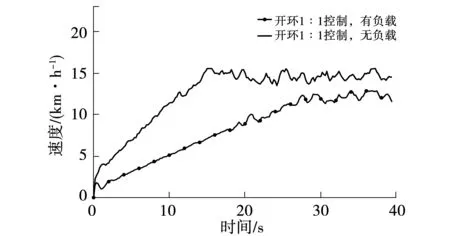
圖14 開環1∶1控制情況下車速對比圖

在自適應控制情況下，給助力車增加30 kg負載后，與無負載相比，起步速度并沒有發生顯著改變，如圖15所示，說明自適應控制系統能較好的適應載重變化，保證車輛的行駛狀態不受載重變化干擾。

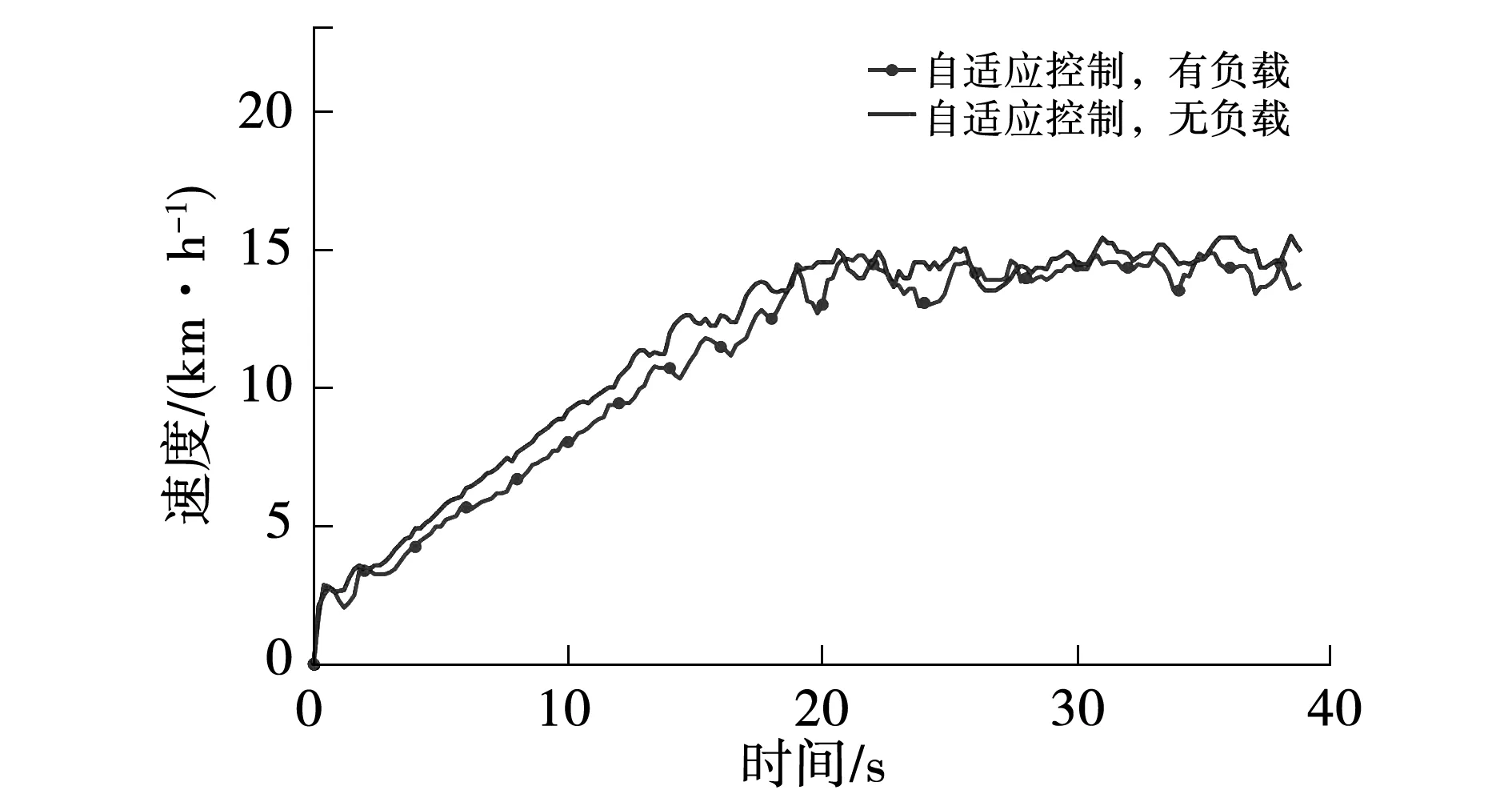
圖15 自適應控制情況下車速對比圖

圖16為車輛在自適應控制情況下，在有負載和無負載兩種狀態下勻速行駛的相電流波形圖，給助力車增加30 kg負載后，相電流比無負載狀態下增加約4 A，助力扭矩隨電流增加而增大，說明自適應控制系統可以依據載重變化對電機輸出扭矩做出動態調整。

圖16 自適應控制情況下相電流對比圖

3.2.2 上坡騎行實驗

實驗條件設置如下：電動助力車由平坦筆直道路行駛進入20%坡度的上坡道路，無障礙物干擾，控制器軟件層面設置恒定踩踏力矩為15 N·m和18 r/min最大踩踏頻率，無任何負載。

圖17為電動助力車在平坦路面起步，速度穩定后進入上坡路段過程中的速度變化。助力車在38 s前行駛在平坦路面，自適應控制系統與開環1∶1控制系統無顯著差別，在38 s時進入上坡路段，由于橫向重力分量增大，行駛阻力增加，開環1∶1控制情況下行駛速度急劇下降，而自適應控制情況下行駛速度緩慢下降，沒有發生速度驟變的情況，說明自適應控制系統能很好的補償上坡路段帶來的前行阻力，從而獲得較好的上坡騎行體驗。與仿真結果相比，實車路況實驗中，自適應控制情況下電動助力車由于地面摩擦阻力、縱向風阻力、電機扭矩傳動損耗等原因，15 N·m踩踏力矩提供的助力扭矩比理想情況下略小，故在上坡后速度逐漸減小。

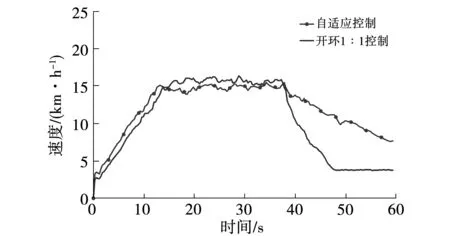
圖17 行駛速度對比圖

圖18為電動助力車在平坦路面起步，速度穩定后進入上坡路段過程中的相電流變化，可以看出，在進入上坡路段后，自適應控制系統逐漸增大相電流，助力扭矩隨著相電流增大而變大，以提供助力車上坡的動力，而開環1∶1控制系統的相電流發生震蕩，平穩后相電流值不變，助力扭矩不變，上坡動力不足，因而速度驟減。

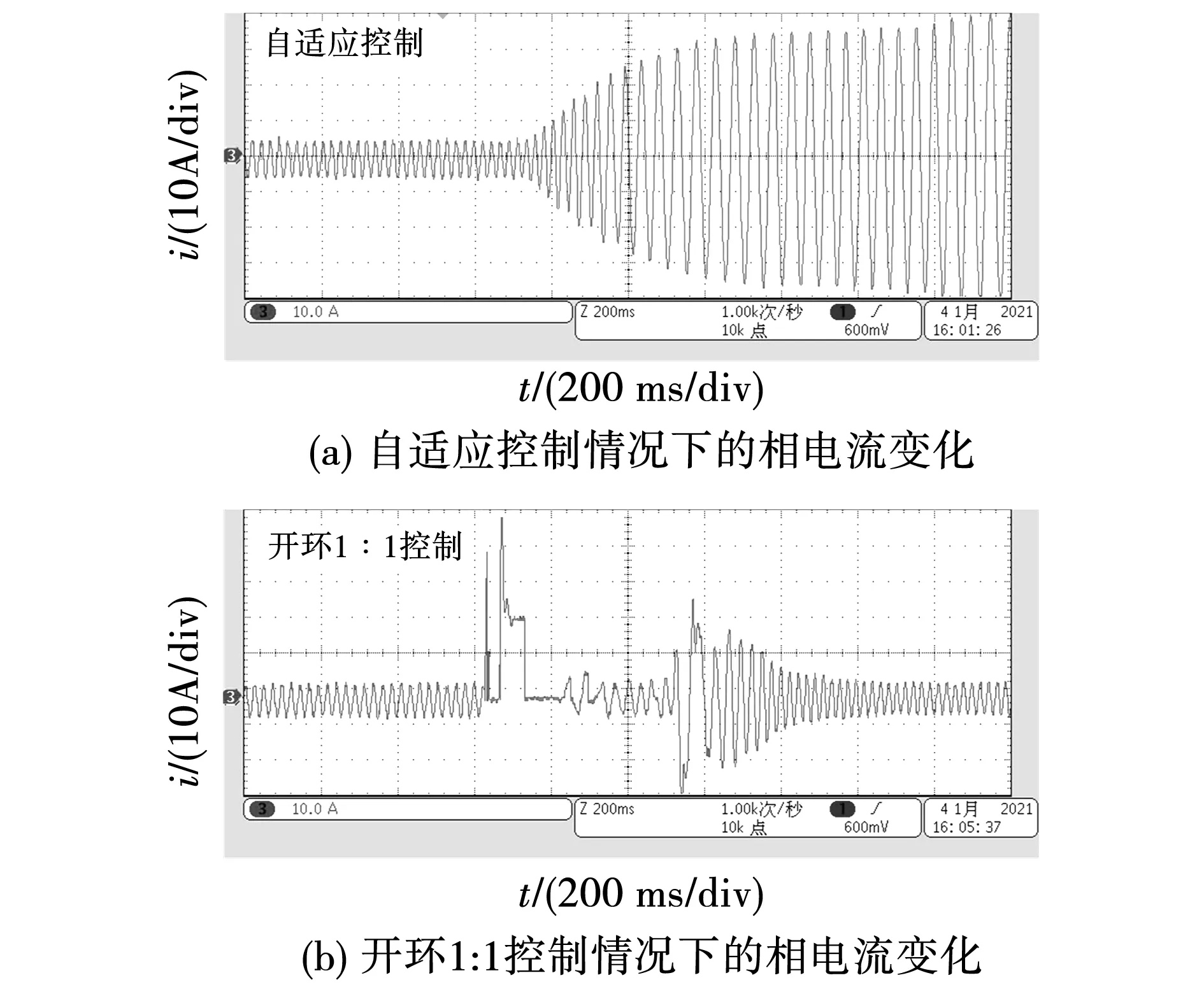
圖18 相電流對比圖

由以上曲線分析可知，使用自適應控制算法可以顯著提升電動助力車的助力效果，在載重變化和坡度變化時，與傳統開環1∶1控制算法相比，助力車的起步速度和上坡能力都有較大的提高，證明了自適應控制算法的有效性，與文獻[7]和文獻[9]相比，由于模型簡單，在力的跟隨性方面得到優化，體現在起步、上坡時候力的及時性傳導，對踩踏力響應變快，且該自適應算法對電機控制器主控芯片的資源占用較少，對芯片算力要求較低，有效降低了控制器成本，在實車路況實驗中系統運行穩定，符合預期效果。

4 結 論

針對當前電動助力車助力系統的要求，本文提出了一種基于模型參考自適應的電助力單車扭矩控制策略。

1)使用Lyapunov第二法推導出系統的自適應率和控制率，保證了系統的全局穩定性，無需單獨證明系統穩定狀態；并使用MATLAB在電動助力車仿真模型中進行驗證，結果證明在車輛負載變化或者道路坡度變化情況下，自適應算法為可以為電動助力車提供有效的助力扭矩。

2)通過實車路況測試，對比自適應控制算法和開環1∶1控制算法的實際騎行效果，對比結果證明自適應控制算法在電動助力車起步速度和上坡能力等方面都有顯著提高，且系統運行穩定可靠。