LNG泵用低溫高速永磁電機偏心故障動態電磁力
戈寶軍, 劉海濤, 王立坤, 林鵬, 溫亞壘
(哈爾濱理工大學 電氣與電子工程學院,黑龍江 哈爾濱 150080)
0 引 言
LNG(液化天然氣)以其清潔環保的屬性得到了各國的廣泛應用,我國LNG進口量逐年增加[1]。LNG的儲存與運輸過程多使用LNG泵,作為LNG泵的核心部件,為保證安全性,電機實驗通常在液氮(-196 ℃)中進行[2]。LNG泵需配備振動檢測裝置來監測泵體的振動情況,而電機定轉子電磁力是電機振動噪聲的主要來源之一,尤其是發生偏心故障時,電磁力會因磁場的畸變呈不對稱分布,嚴重影響電機性能,甚至對電機造成破壞。因此,探討永磁同步電機在-196 ℃下的動態電磁力分布,闡述其與常溫(25 ℃)下電磁力的差異性,找出應力集中的位置,對低溫電機的振動研究和結構改進具有理論和實際指導意義。
文獻[4]根據定子繞組和導條電導率的變化對LNG泵用低溫異步電機進行了重新設計,考慮低溫下磁密分布特征和磁飽和的影響,仿真了低溫電機的運行特性。文獻[5]根據低溫環境要求,設計制造了一臺永磁體位于轉軸內部的高速凸極電機,定子為無槽結構,并對低溫環境下電機的材料和工藝進行了說明。文獻[6-7]在設計的低溫永磁電機基礎上,對電機的電磁特性和機械特性進行了重點研究。文獻[8-10]對LNG泵用低溫異步電機關鍵技術進行了較為細致的研究,對低溫異步電機的電磁設計方案、電機在液氮中的運行性能及電機導液通道的優化進行了探討,并進行了樣機實驗。分析發現,現有文獻多針對低溫異步電機開展研究,對低溫高速永磁電機的研究還處于初始設計與實驗測試階段。
國內外學者對電機電磁力的計算方法和故障下電磁力分布的研究已經做了許多工作。文獻[11]基于虛位移原理,在鐵磁材料能量表達式的基礎上推導了同時適用于線性和非線性材料的電磁力計算公式,并依據此種方法計算了汽輪發電機鐵心電磁力的分布。文獻[12]對原有麥克斯韋張量法的計算公式進行了拓展,新公式可以考慮區域邊界磁場不連續的情況,允許對永磁體全局或局部電磁應力進行計算。文獻[13]采用攝動法建立了完整的環形繞組無刷直流電機解析模型,用麥克斯韋張量法計算了電機偏心時的徑向電磁力,并與有限元法互相驗證。文獻[14-15]分別對電機發生斷條和單相接地故障時的電磁力進行了計算,對比研究了故障下電磁力的分布特征。文獻[16]在對永磁直驅發電機偏心和短路故障電磁力計算的基礎上,進一步對由電磁力引起的轉子機械應力進行了研究。文獻[17]優化了保角變換法,獲取了一臺永磁同步電機的氣隙磁場偏心特性,以此對電機的電磁力進行深入計算和分析。上述文獻在對電機不同狀態下電磁力研究時,并沒有考慮溫度對電機的影響,尚未見到對LNG泵用低溫高速永磁電機電磁力研究的文獻。
本文以LNG泵用低溫高速永磁電機為研究對象,對比研究低溫與常溫環境下電機電磁力特性的差別,分析偏心故障時轉子護套表面與定子齒部電磁力的變化規律。在常溫電機設計方法的基礎上,提出低溫電機尺寸設計的思路,建立低溫高速永磁電機偏心故障有限元模型,計算故障前后轉子護套表面位置處、定子齒頂及定子齒壁動態電磁力,并對電磁力的計算結果進行驗證。
1 低溫高速永磁電機數學模型和電磁力計算方法
1.1 低溫高速永磁電機修正設計方法與物理模型
電機定子繞組銅線電阻率隨溫度的降低而減小,根據實驗測試數據可將電阻率ρCu擬合成如下與溫度T相關的函數[8]為
ρCu(T)=7.01×10-11T+1.6×10-8。
(1)
低溫高速永磁電機的永磁體材料需選用溫度系數較低的釤鈷材料。將釤鈷永磁體Sm2Co17浸泡在-196 ℃的液氮中進行測試,其剩磁相比于25 ℃提高了6.5%左右[7]。
考慮溫度的影響,定子電阻與空載反電勢為:
(2)
式中:R(T)定子繞組;Ns為每相串聯導體數;L為繞組平均半匝長;S(T)為槽面積;E(T)為空載反電勢;V(T)和Bsr(T)分別為永磁體體積和剩磁。
低溫下定子電阻與空載反電勢發生改變,初始設計時,為保證電機在低溫下仍具有與常溫電機相同的輸出性能,空載反電勢和定子電阻應保持不變:

(3)
由式(2)、式(3)可得-196 ℃和25 ℃時的槽面積和永磁體體積有如下關系:
(4)
從式(4)可以看出,與25 ℃相比,-196 ℃時定子槽面積和永磁體體積分別隨著電阻率的降低和剩磁的增加而減小。兩種設計溫度時,定子槽和永磁體尺寸示意圖如圖1所示,表1給出了-196 ℃情況下電機的額定參數。
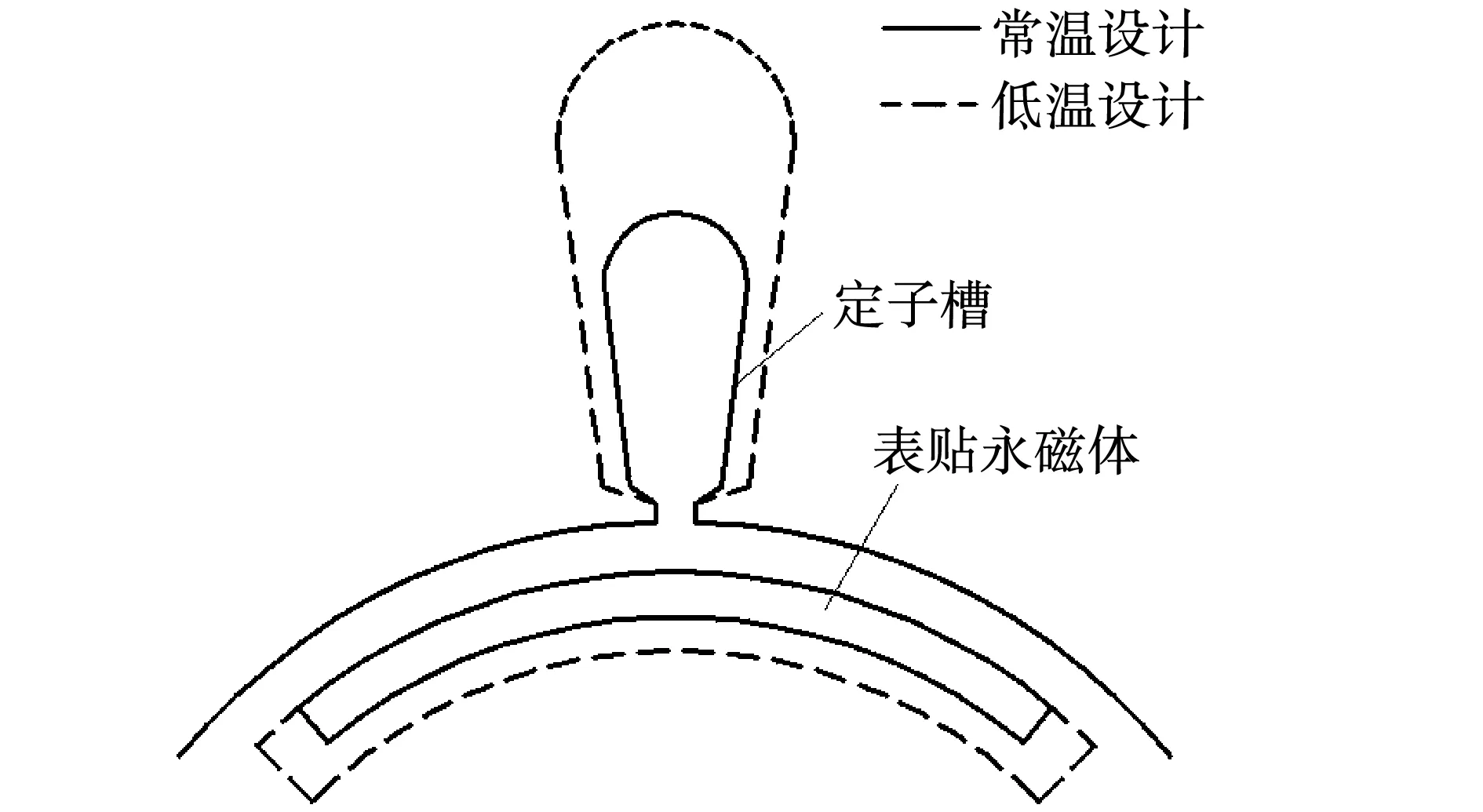
圖1 尺寸對比示意圖
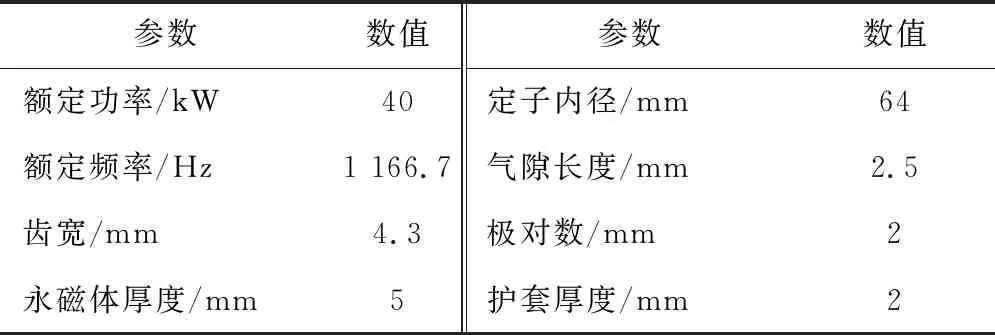
表1 低溫高速永磁電機主要參數
低溫高速永磁電機的物理模型如圖2所示。相比于不銹鋼與鈦合金護套,本文應用的碳纖維護套在高速下產生的渦流損耗較低、所需過盈量較小[18],而碳纖維散熱性較差的缺點在本文研究的低溫環境下也可忽略不計。此外,低溫高速永磁電機冷卻效果好,因此溫度過盈量較小,根據護套與永磁體間總過盈量與裝配過盈量和溫度過盈量之間的關系可知[19],若要保證低溫電機與常溫電機具有相同的總過盈量,即低溫與常溫下護套的應力處于同一水平,在其他相關因素均相同時,可通過減小低溫電機的裝配過盈量來實現。由于低溫高速永磁電機所需的裝配過盈量更小,過盈量對電機電磁場的影響微弱,故本文在計算電機電磁力的過程中忽略護套與永磁體間過盈量的影響。
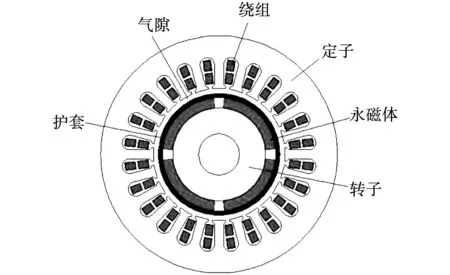
圖2 低溫高速永磁電機物理模型
1.2 低溫高速永磁電機偏心故障有限元模型建立
當電機發生機械故障時,絕大多數都會引起電機偏心[20]。電機在偏心情況下其坐標系示意圖如圖3所示。
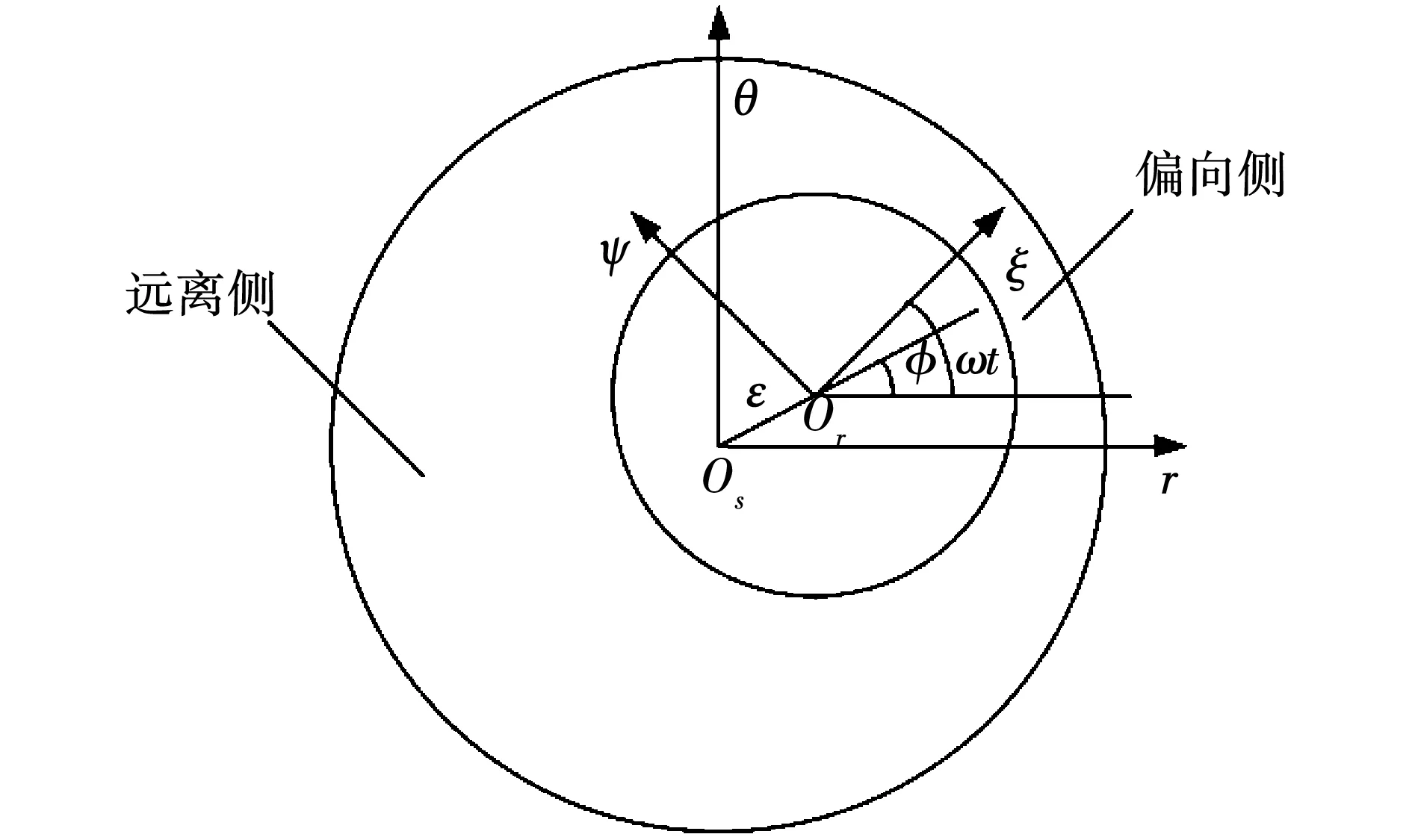
圖3 電機偏心坐標系
圖3中:Os為定子靜止坐標系r-θ的原點;Or為轉子旋轉坐標系ξ-ψ的原點;ε為偏心距離;φ為偏心角;ω為轉子旋轉角速度。
相比于動偏心,靜態偏心時的偏心故障特征更為明顯,本文主要研究低溫電機靜態偏心時電磁力力分布情況。為便于分析,忽略因溫度變化導致的電機機械形變對電機內電磁場與偏心的影響,假設定子內圓與轉子外圓表面均為理想的光滑圓面。無偏心時氣隙長度為δ0,定義偏心率為
(5)
在圖2所示的低溫高速永磁電機模型內,電機瞬態電磁場微分方程表示為
(6)
式中:Az和Jz為矢量磁位和電密的軸向分量;μ為磁導率;σ為電導率;L1為定子鐵心外圓邊界。
1.3 護套表面位置處與定子齒部電磁力計算方法
低溫高速永磁電機轉子表面設有碳纖維護套,護套和LNG與空氣磁導率接近,假設其相對磁導率均為1。對于護套表面位置處,其徑向與切向電磁力可按氣隙磁場的電磁力進行計算:
(7)
式中:fr為徑向電磁力;fθ為切向電磁力;Br為徑向磁密;Ht為切向磁密;μ0為空氣磁導率。
低溫電機發生偏心時,氣隙縮小側為偏向側,氣隙增大側為遠離側,在偏心故障發生后,偏向側定子齒部磁密大于遠離側,如圖4所示。選取距離轉子中心最近和最遠處的定子齒為研究對象,分別用P和O表示,并在齒壁重要位置處選取10個采樣點,令1,3,5,7,9為齒壁前側,2,4,6,8,10為齒壁后側。
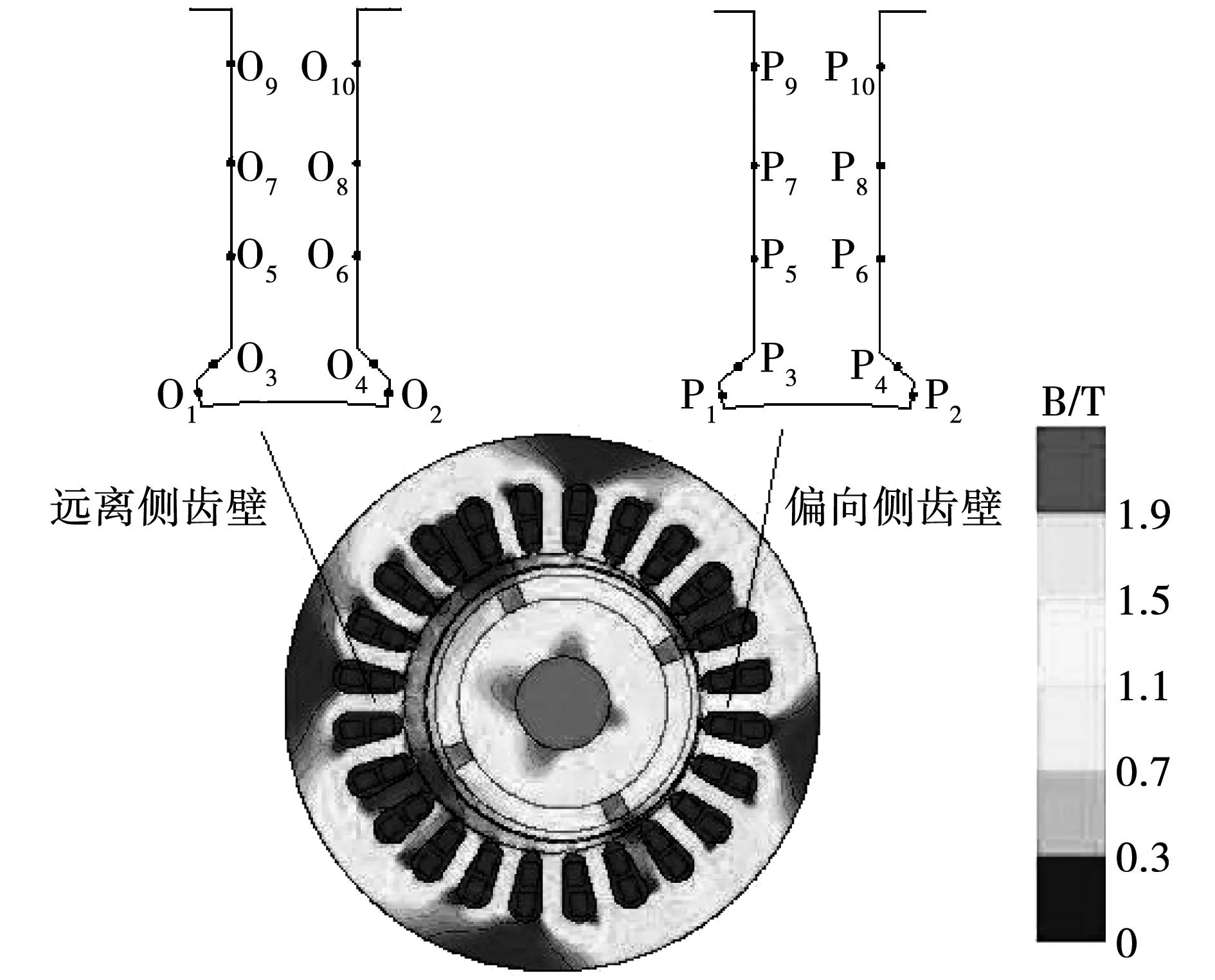
圖4 偏心磁場分布
考慮磁飽和時,采用麥克斯韋張量法計算定子齒頂和齒壁與空氣交界面處的電磁應力[21]
(8)
式中:μFe為鐵心磁導率;fθ為電磁力切向分量;fr為電磁力法向分量。
2 低溫高速永磁電機偏心前后護套表面位置處動態電磁力計算
低溫與常溫情況下護套表面徑向和切向電磁力分布情況分別如圖5和圖6所示。
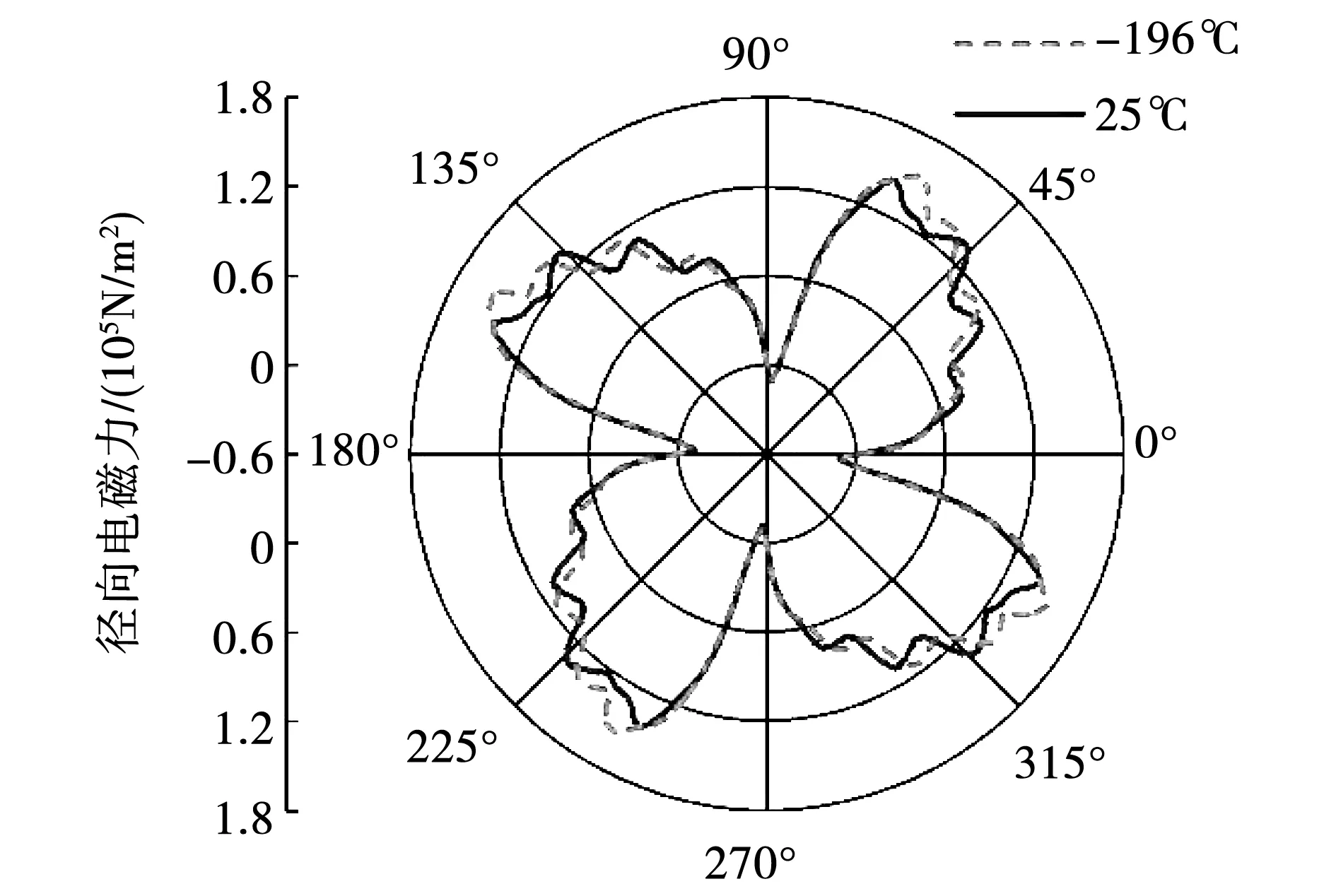
圖5 不同溫度下護套表面位置處徑向電磁力
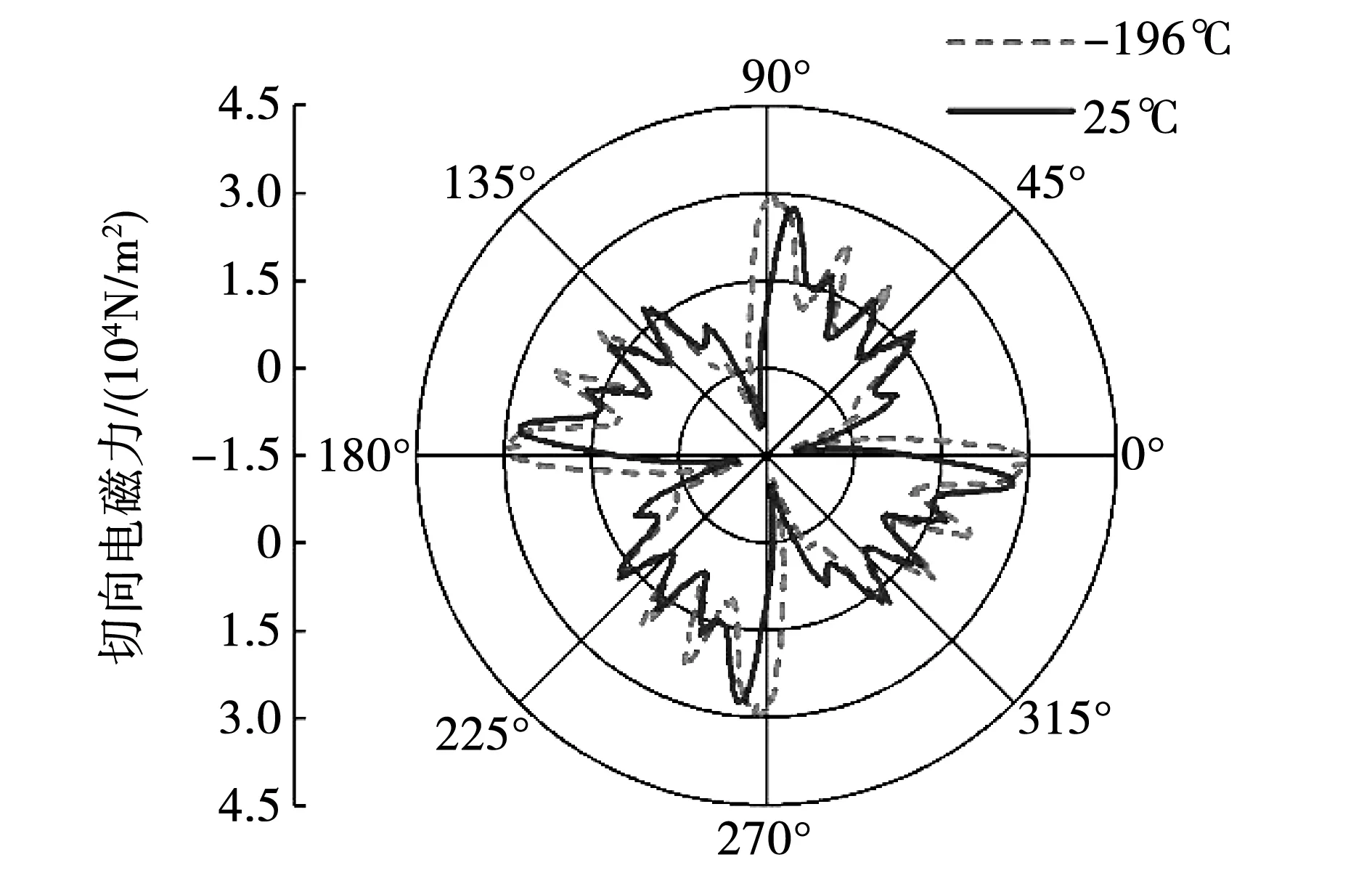
圖6 不同溫度下護套表面位置處切向電磁力
由圖5可以看出,護套表面位置處徑向電磁力呈周期分布,其周期數與低溫電機極數一致。相比于常溫情況下,低溫時護套表面位置處徑向電磁力有所增加,25 ℃時其峰值為1.43×105N/m2,-196 ℃時其峰值為1.54×105N/m2,增加7.14%。同時,受電機齒槽效應影響,定子齒部對應的護套表面位置處的電磁力大于定子槽部。
由圖6可知,-196 ℃時切向電磁力峰值為2.99×104N/m2,比25 ℃增加8.30%,-196 ℃時切向電磁力峰值是徑向電磁力峰值的0.19倍,且一個周期內切向電磁力有效值是徑向電磁力有效值的0.15倍,切向電磁力遠遠小于徑向電磁力。
低溫電機不同偏心率的情況下護套表面位置處徑向電磁力的分布狀態如圖7所示。與圖5相比,偏心時電磁力發生不規則變化。偏向側氣隙較小,磁密較大,電磁力隨偏心率的增加而增大,而遠離側電磁力則與之相反。偏心率為10%時電磁力峰值為1.68×105N/m2,而偏心率為50%時電磁力峰值達到最大,為2.86×105N/m2,增加了41.26%,與無偏心時運行于-196 ℃和25 ℃時相比,分別增加46.15%和50.00%。
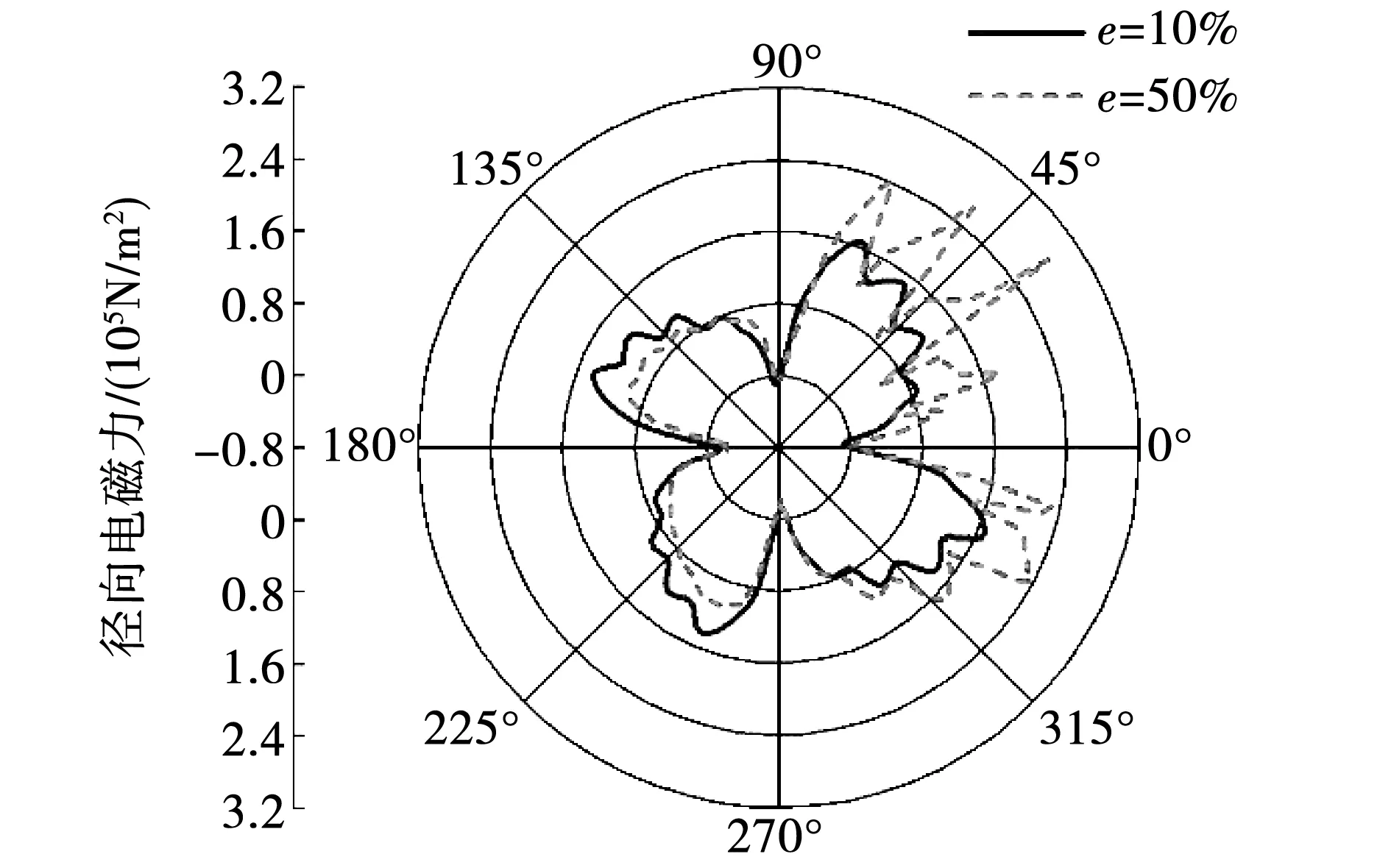
圖7 不同偏心率時護套表面位置處徑向電磁力
3 低溫高速永磁電機偏心前后定子齒頂動態電磁力計算
圖8給出了電機分別負載運行于-196 ℃和25 ℃時定子齒頂電磁力沿圓周的分布情況。從圖可以看出,電機無偏心時不同極下電磁力分布規律相同,由于電樞反應的影響,一個極下每個齒頂的電磁力大小不同,且分別在機械角為30.6°、120.6°、210.6°、300.6°時齒頂電磁力達到峰值。25 ℃時齒頂電磁力峰值為3.05×105N/m2,-196 ℃時齒頂電磁力峰值為3.68×105N/m2,相比增加16.30%。
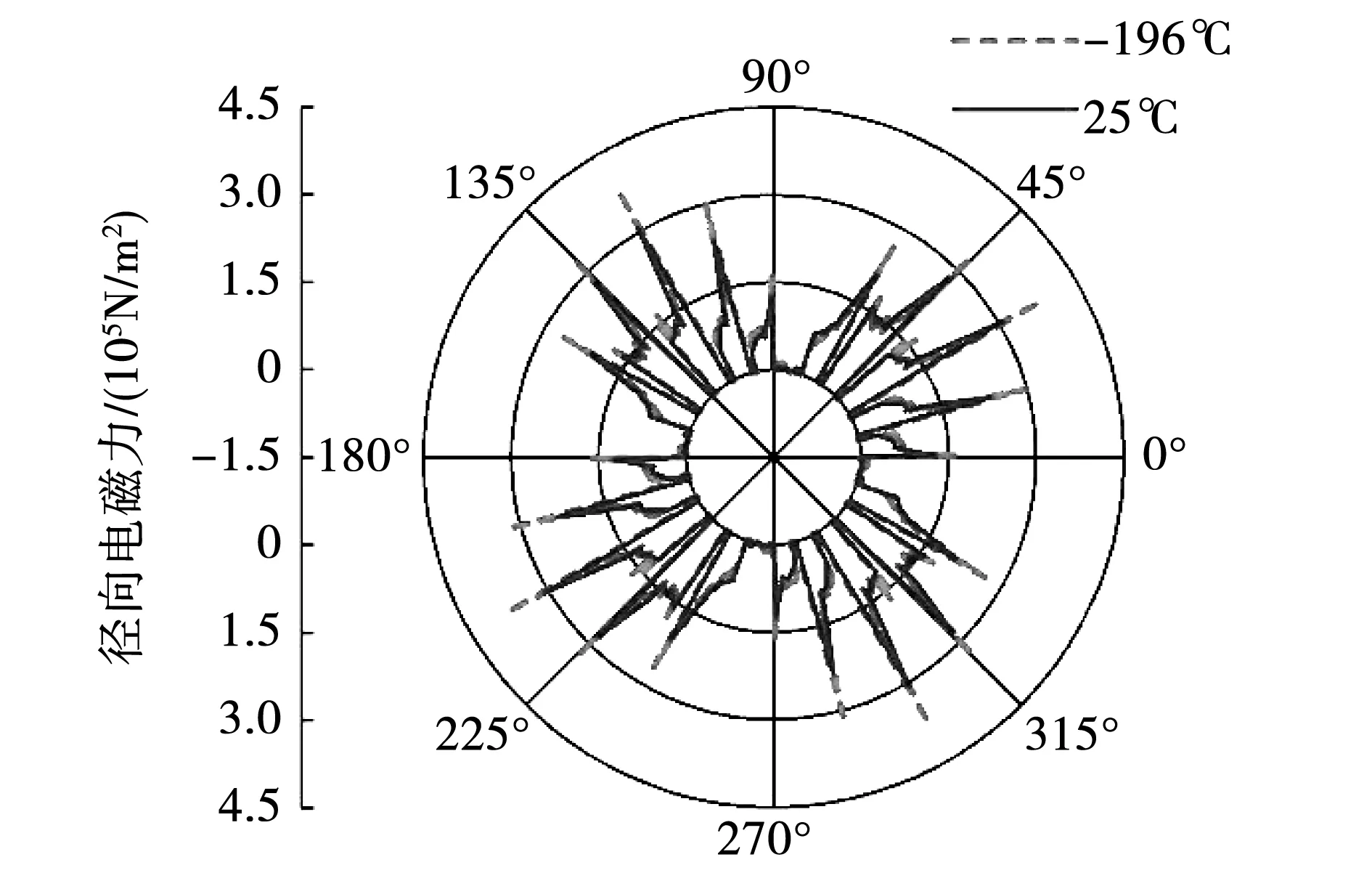
圖8 不同溫度下齒頂徑向電磁力
圖9給出了偏心率為10%和50%時齒頂徑向電磁力的分布。如圖所示,與轉子護套表面徑向電磁力分布類似,發生不同程度偏心故障后,定子齒頂電磁力呈不對稱分布,偏向側與遠離側受力不等,使得定子鐵心受力不平衡。偏心率為10%時偏向側齒頂電磁力峰值為4.00×105N/m2,偏心率為50%時為7.85×105N/m2,相比增加了49.04%,而遠離側齒頂電磁力峰值降低了19.89%。與-196 ℃和25 ℃未發生偏心故障相比,低溫高速永磁電機偏心率為50%時偏向側齒頂電磁力峰值分別增加了53.1%和61.15%,可見低溫環境下偏心故障后齒頂電磁力增加較為明顯,從而加大定子鐵心的振動和形變。
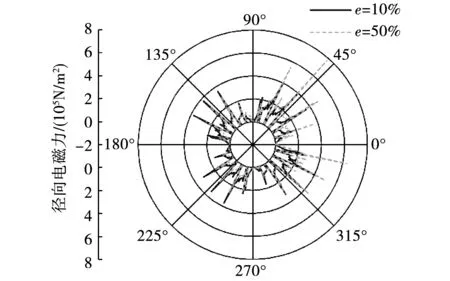
圖9 不同偏心率時齒頂徑向電磁力分布
4 低溫高速永磁電機偏心前后定子齒壁動態電磁力計算
在-196 ℃無偏心時,齒壁前側與后側各點電磁應力隨時間變化規律類似,圖10給出了-196 ℃時一個電周期內齒壁前側各采樣點的電磁力隨時間變化曲線。由圖可知,P5、P7和P9點電磁力變化趨勢相似,位于齒壁中部的P5與P7兩點電磁力數值基本一致,位于槽底附近的P9點電磁力數值最高,而齒肩P3點幅值最小。這是由于定子齒頂和齒肩比定子齒身寬,雖然P1與氣隙距離較小,但綜合而言,位于齒身的P5、P7和P9點的磁密較大,這一結論與圖4相符,故磁密較大的位置電磁應力也較大。
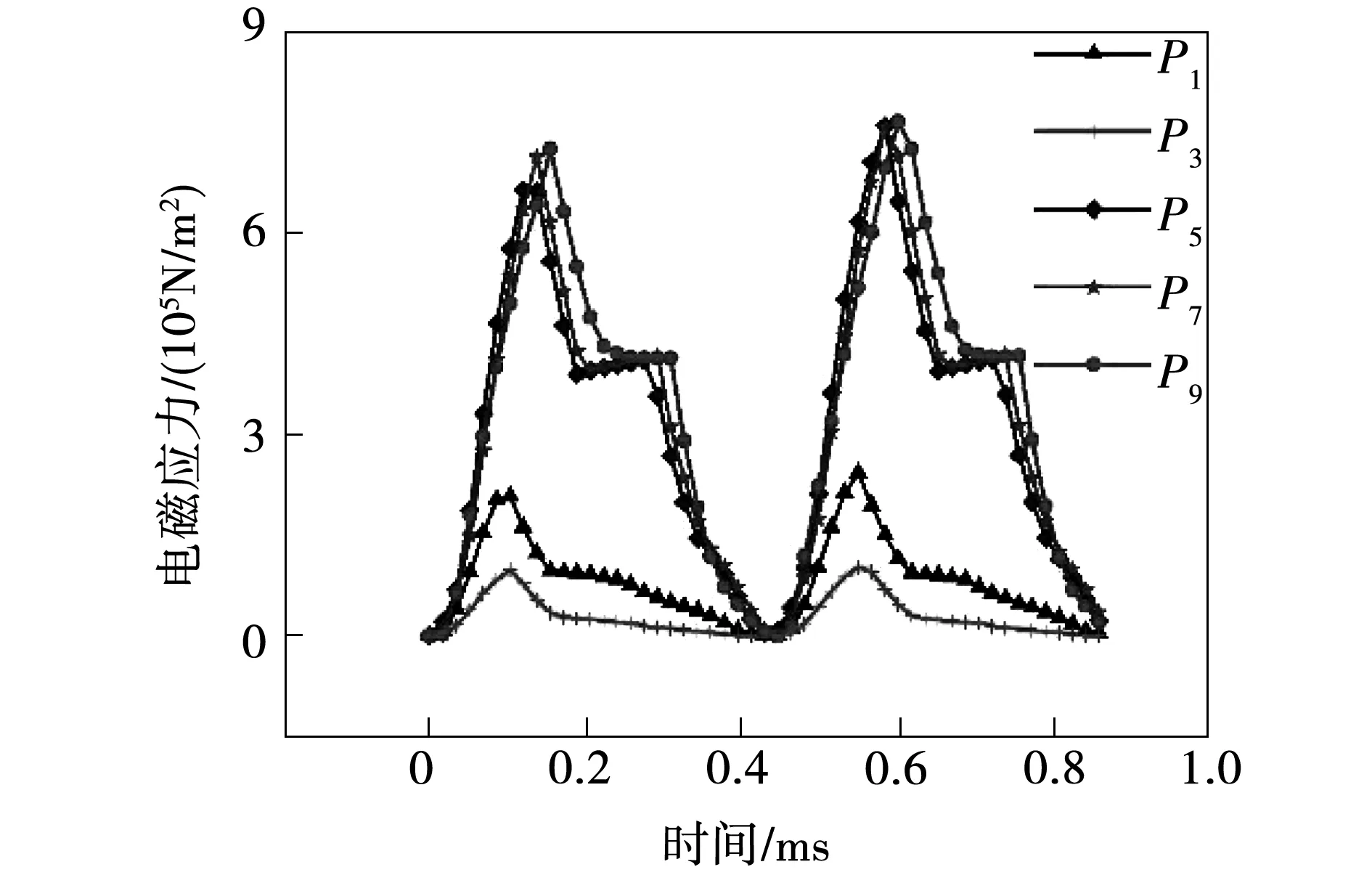
圖10 低溫下齒壁前側電磁應力分布
偏向側齒壁各采樣點電磁力在不同溫度下比較情況如表2和表3所示。
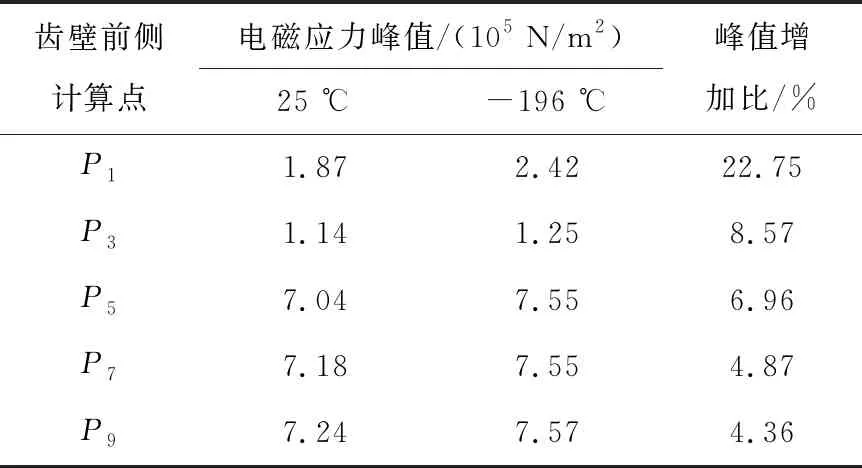
表2 齒壁前側電磁應力峰值
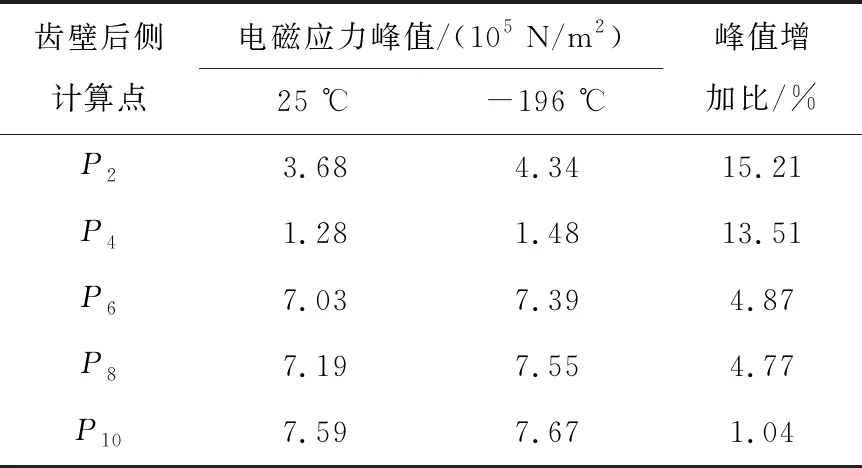
表3 齒壁后側電磁應力峰值
由表2和表3可知,無論齒壁前側還是齒壁后側,其電磁應力峰值的變化趨勢都表現為:離槽底越近,數值越大。并且各點-196 ℃時電磁應力峰值都大于25 ℃時的電磁應力峰值。但是,峰值增加比卻隨著離槽底越近,數值越小。這是由于隨著溫度降低,永磁體剩磁增大,使遠離槽底的采樣點電磁力增加幅度變大。
齒壁后側的電磁應力峰值大于齒壁前側,故選取采樣點P2和P8、O2和O8為研究對象,討論各點在不同偏心率下電磁力分布情況。圖11給出了在低溫情況下P2點和O8點的電磁力分布。
從圖11可以看出,在同一時刻,P2點電磁應與偏心率成反比,而O8點電磁應力與偏心率成正比,二者隨偏心率變化的趨勢相反。類似地,與P2和O8對應的偏向側P8和遠離側O2點遵循同樣的變化規律。
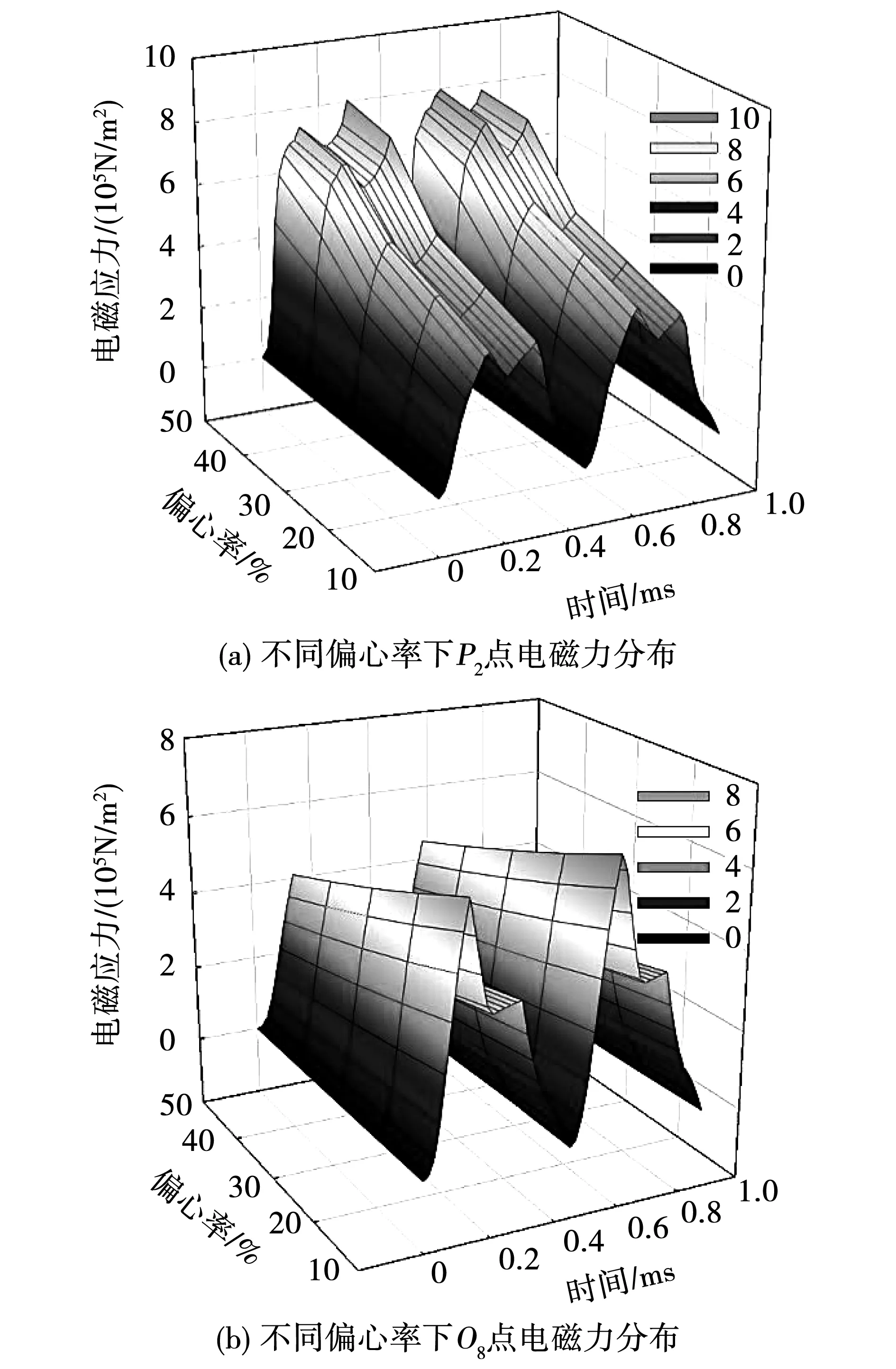
圖11 不同偏心率下關鍵點電磁力分布
圖12給出了電機工作在-196 ℃不同偏心率時,相對于-196 ℃不偏心和25 ℃不偏心時齒壁關鍵點電磁應力峰值增加比的變化規律。由圖12可知,當電機工作在-196 ℃且發生偏心故障時,P2點與P8點的電磁應力增加比與偏心率大小成正相關,O2點與O8點成負相關。同時,P8點和O8點電磁應力增加比在整個偏心率范圍內近似成直線變化,而P2點與O2點存在變化平緩區域。此外,偏心率為50%時圖12中各計算點電磁應力增加比達到最大,其中P2點電磁應力相對于-196 ℃不偏心時的增加比為46.09%,相對于25 ℃不偏心時的增加比為54.29%,而P8點增加比分別為32.23%和35.46%。可以看出,雖然P2點的電磁應力峰值小于P8點,但在發生偏心時,P2點電磁應力峰值增加比大于P8點。
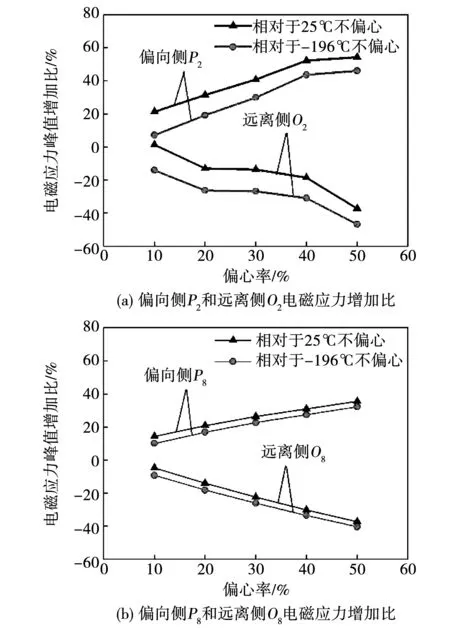
圖12 電磁應力峰值增加比
5 電磁力計算結果的合理性驗證
1)電磁轉矩的驗證。切向電磁力主要產生切向電磁轉矩,具體為

(9)
式中Lef為電機有效長度。
為了驗證低溫高速永磁電機正常運行時的電磁轉矩,對比分析虛位移法和切向電磁力計算結果,如圖13所示。
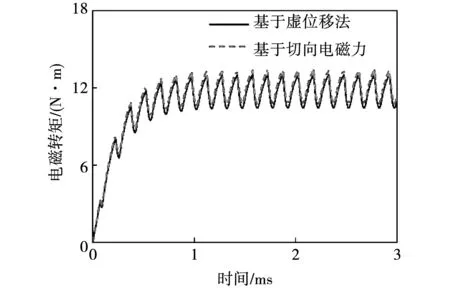
圖13 電磁轉矩
由圖13可知,基于切向電磁力得到的電磁轉矩略大于經典虛位移法計算的結果,兩種方法計算的電磁轉矩穩定后平均值相差1.97%,證明本文切向電磁力計算結果準確。
2)表4給出了有限元法和解析法的低溫電機電磁場計算結果,兩種方法計算結果基本相同,驗證了電磁力計算結果的準確性。
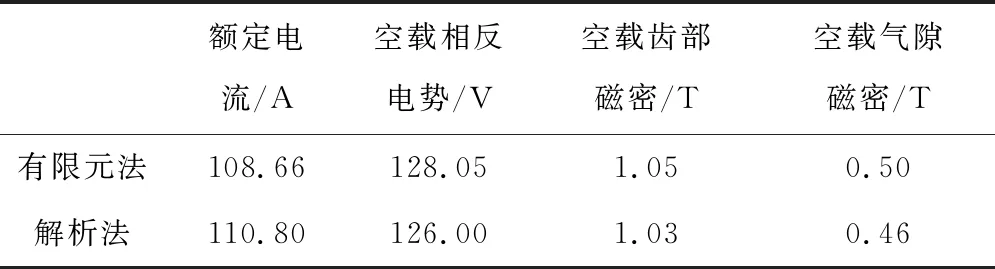
表4 電磁場計算結果
3)氣隙徑向電磁力時空特性驗證。由磁路法,氣隙磁密可表示為氣隙磁勢f(θ,t)和氣隙磁導λ(θ,t)的乘積:
Br(θ,t)=f(θ,t)λ(θ,t)。
(10)
以磁導的變化體現靜偏心的影響,偏心后氣隙磁導[3]近似表示為
(11)
由式(11)可知,靜態偏心時氣隙磁導不隨時間變化,故靜態偏心不會電機的頻率分布產生影響。
根據式(10)和式(11)可得偏心附加磁場對應的氣隙磁密瞬時值為
(12)
式中:μ、ν分別為定子和永磁體諧波次數;Bμ、Bν分別為定子μ次諧波幅值、永磁體ν次諧波幅值;φμr為μ次諧波初始角;θ為機械角度;ω1、ωνr分別為基波角頻率和永磁體ν次諧波角頻率。
忽略次數高、幅值較小的次要分量和對振動噪聲無影響的直流分量,根據式(7)可得偏心附加磁場產生的附加氣隙徑向電磁力為
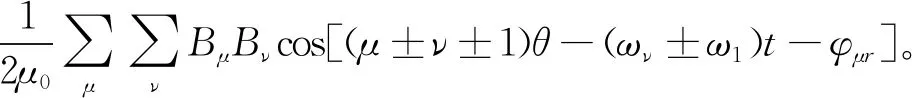
(13)
式中:等號右側第一項為附加磁場產生的與無偏心時電磁力諧波階數相同的力波分量;第二項表示附加磁場產生的μ±ν±1階力波分量,頻率不變。
無偏心時,定轉子基波產生的徑向電磁力為
(14)
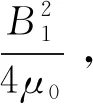
由以上解析公式分析可得低溫高速永磁電機偏心故障前后氣隙徑向電磁力時空分布特性為:
1)靜態偏心只改變電機空間位置,最小氣隙位置不變,氣隙徑向電磁力頻率分布與故障前相同,其中2倍頻對應的電磁力分量幅值最大。
2)電機無偏心時,氣隙磁密只包含奇數次諧波,氣隙徑向電磁力只含有偶數次諧波;發生偏心故障后,氣隙磁密同時含有奇數次和偶數次諧波,氣隙徑向電磁力在原有諧波兩側新增±1階諧波。
3)由偏心附加磁場產生的附加徑向電磁力會與原有同階次以及同頻率的電磁力相疊加,故障后徑向電磁力各階次、各頻率對應的幅值有所增加。
以50%偏心率為例,圖14(a)給出了偏心故障前后氣隙內某點徑向電磁力的頻譜圖(基頻f=1 166.67 Hz),其中0 Hz是直流分量,不會對電機電磁振動產生影響,頻率為2f的徑向力分量幅值最大,且故障后各倍頻率幅值均增加。圖14(b)給出了偏心故障前后某一時刻氣隙徑向電磁力空間諧波階次圖。由圖14(b)可知,無偏心時電磁力只含有偶數次諧波,故障后在偶數次諧波兩側新增了±1次諧波,產生了奇數次諧波,且偶數次諧波幅值均大于故障前。此外,無偏心時圖14(a)各倍頻幅值與圖14(b)中同次數諧波的幅值存在對應相等關系,故障后則無此對應關系,且偏心后定子齒諧波引起的力波分量增加明顯。數值計算得到的氣隙徑向電磁力時空特性與解析分析結果一致。
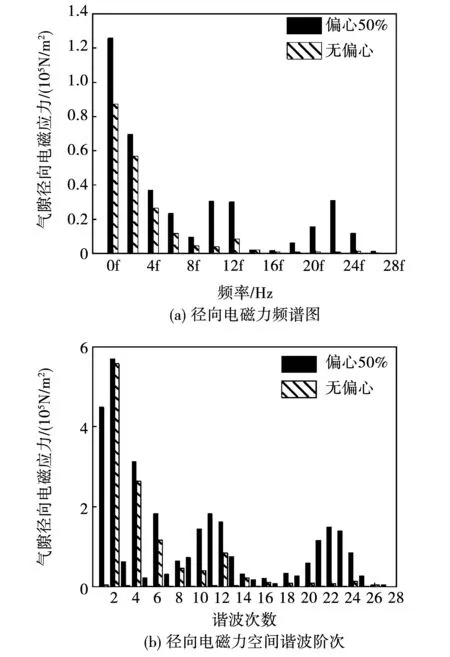
圖14 徑向電磁力時空特性
6 結 論
本文給出了低溫高速永磁電機與常溫電機的差異性設計方法,結合麥克斯韋張量法對低溫環境下偏心故障前后電機全域內電磁力進行計算,最后對電磁力的計算結果加以驗證。通過對低溫高速永磁電機電磁力計算結果的分析可得到如下結論:
1)無偏心時,與工作在25 ℃下相比,低溫-196 ℃時電機定、轉子電磁力峰值均有所增加,其中定子齒壁前側和后側各關鍵點電磁應力增加比隨著計算點遠離槽口而降低。低溫環境下不改變電磁力分布趨勢,只影響幅值。
2)發生偏心故障后,轉子護套表面和定子齒頂徑向電磁力分布不對稱,電磁力最大位置位于偏向側氣隙較小處,與偏心率成正比;遠離側電磁力較小,與偏心率成反比。
3)偏心率最大為50%時,齒壁靠近槽口處的P2點電磁應力增加比達到最大,相對于-196 ℃無偏心和25 ℃無偏心時分別增加46.09%和54.29%。
4)低溫高速永磁電機偏心故障后齒頂與槽口處的齒壁關鍵點電磁應力變化較大,可作為電機偏心故障監測與診斷的參考位置,應重點關注其模態及結構力學特征。

